Doğrusal denklem dizgesi, birkaç tane aynı tip değişkenleri içeren birkaç tane doğrusal denklemlerin oluşturduğu topluluktur. Örneğin:

Burada üç çeşit değişken , ile bulunur ve bu üç değişken üç ayrı doğrusal denklem içindedir ve böylece doğrusal denklemler (sistemi) dizge elde edilir.
Bir doğrusal dizgenin çözümü bilinmeyen değişkenlere, tüm doğrusal denklemleri aynı zamanda tatmin eden, reel sayıların tahsis edilmesidir. Yukarıdaki denklemler dizgesi için çözüm kümesi bulunur ve bu
olur.
Doğrusal denklem dizgeleri mühendislik, fizik, kimya, bilgisayar bilimi ve ekonomide pek çok uygulama alanı bulur.
Genel şekil
n bilinmeyen değişkenli m sayıda doğrusal denklemden oluşan bir doğrusal denklen dizgesi genel olarak şöyle yazılabilir:

Burada 




Çok kere katsayılar ve bilinmeyen değişkenler reel sayılardır. Fakat ileri matematikte bunlar karmaşık sayılar, tam sayılar, polinomlar ve hatta soyut cebirsel yapılar bile olabilirler.
Vektör denklemi
Bu genel doğrusal denklemler dizgesini uygun bir şekilde ifade edilmesi vektörler halinde olur: Bu ifade şeklinde her bir değişken bir bir ağırlık olarak bir sütun vektör ile ifade edilmektedir.
Matris denklemi
Vektör denklemine aynen tekabül eden ve matriks kullanılarak ifade edilen genel doğrusal denklemler dizgesi şu şekilde ifade edilir:
burada A m×n matrisi, x içinde n tane ifade bulunan bir ve b içinde m tane sabit ifade olan bir sütun vektörü olur.
Çözüm kümesi

Bir doğrusal denklem dizgenin çözümü, bilinmeyen değişkenlere (yani x1, x2, ..., xn değişkenlerine) tüm doğrusal denklemleri aynı zamanda tatmin eden reel sayısal değerler tahsis edilmesidir. Tüm mümkün çözümlerin bir matematiksel kümesine çözüm kümesi adı verilir.
Bir doğrusal denklem dizgesi için üç ve sadece alternatif mümkün sonuç ortaya çıkabilir:
- Sistemin sonsuz sayıda çeşitli çözümü bulunur;
- Sistemin tek bir çözümü bulunur;
- Sistemin hiçbir çözümü bulunmaz.
Geometrik yorum
İki değişkenden (



Üç değişkenli bir dizge için her doğrusal denklem üç boyutlu bir uzayda bir olurlar ve çözüm kümesi bu düzlemlerin kesişmesidir. Böylece çözüm kümesi ya bir düzlem, ya tek bir doğru, ya tek bir nokta ya da boş küme olur.
n sayıda değişken halinde, her bir doğrusal denklem bir bir olarak ortaya çıkar. Çözüm kümesi bu hiperdüzlemlerin kesişmeleridir ve n-ye kadar herhangi bir boyutta olabilir.
Genel sonuç hali

Genel olarak, bir doğrusal denklemler dizgesinin sonucunun ne olabileceği, denklemler sayısı ile bilinmeyen değişkenler sayısı arasındaki bağlantılar tarafından belirlenir:
- Genellikle, eğer dizgede denklem sayısı bilinmeyen değişken sayısından daha küçükse ise, dizge için sonsuz sayıda çözüm bulunur. Fakat bazen tek bir "seyrek çözüm" bulma imkânı da vardır. Yani kullandığımız notasyona göre m < n ise, sonsuz çözüm vardır. Bu çeşit dizgelere kararsız dizge (underdetermined system) adı verilir.
- Genellikle, eğer dizgede denklem sayısı değişken sayısı ile aynı ise, tek bir tane çözüm bulunur; yani m = n ise tek ve tek bir çözüm bulunur.
- Genellikle, eğer dizgede denklem sayısı değişken sayısıdan daha büyük ise hiçbir sçözüm bulunmaz; yani m > n ise hiçbir çözüm bulunmaz.
Aşağıdaki gösterimler iki değişkenli halde ortaya çıkabilmesi mümkün üçlü sonucu göstermektedir:
![image]()
![image]()
![image]()
Bir Denklem İki Denklem Üç Denklem
Verilen gösterimede; birinci dizgenin sonsuz sayıda çözümü bulunur; yani bunun noktaları mavi renkli doğru üzerindedir. İkinci dizgede tek bir çözüm bulunur; yani iki doğrunun kesişme noktası çözümdür. Üçüncü sistemde bulunan üç doğrunun ortaklaşa hiçbir noktaları bulunmaz.
Fakat şunu unutmamak gerekir; bütün bu sonuçlar sadece genellikle doğrudur. İki denklemeli ve iki değişkenli bir dizgenin hiçbir çözümü olmaması mümkündür; bu hal her iki doğru birbirine paralel ise ortaya çıkar. Üç denklemle iki değişkenli bir dizgenin çözümü olması mümkündür; bu hal eğer üç doğru birbiriyle tek noktada kesişirlerse ortaya çıkar. Genel olarak; bir doğrusal denklemler dizgesi beklenenden değişik davranış göstermesi eğer denklemler "doğrusal olarak bağımlı" iseler veya iki veya daha çok sayıda denklemlerin "tutarsız" olmaları halinde ortaya çıkar.
Nitelikler
Bağımsızlık
Bir doğrusal denklem dizgesinin denklemleri bağımsızlık niteliği, dizgede bulunan denklem eşitliklerinin hiçbiri denklemden cebirsel olarak çıkartılaması halidir. Eğer denklemler bağımsızlarsa, her bir denklem değişkenler hakkında yeni bilgi kapsamaktadır ve bu denklemlerden herhangi birinin ortadan kaldırılması çözüm kümesinin boyutunu artır. Doğrusal denklemler için mantıksal bağımsızlık özelliğiyle ile aynıdır.

 ,
,  ve
ve  denklemleri doğrusal olarak bağımsız değildirler.
denklemleri doğrusal olarak bağımsız değildirler.Örneğin, şu denklemler
bağımsız değildirler; çünkü ikinci denklem birinci denklemin 2 ile çarpımı ile elde edilmiştir ve eğer bu iki denklem için grafik çizilirse iki doğru üste çakışıp tek bir doğru görüntüsü verirler.
Daha karmaşık bir örnek için verilen denklemler dizgesi şu olsun:
Bu üç denklem dizgesi bağımsız değildir, çünkü üçüncü denklem ilk iki denklemin birbirine toplamından elde edilmiştir. Gerçekten bu üç denklemden herhangi ikisinden üçüncü denklem çıkartılabilir ve bu üç denklemden herhangi tek bir tanesi ortadan kaldırılırsa çözüm kümesi hiç değişmeden aynı kalır. Bu üç doğru için grafik üçü de tek bir noktada kesişen üç doğru şeklindedir.
Tutarlılık
Bir doğrusal denklemler dizgesi denklemleri, eğer bir ortak çözüm varsa, "tutarlı" olur; aksi halde "tutarsız" olur. Eğer denklemler tutarlı iseler; denklemlerden bir ortaya çıkartmak imkânı bulunur; örneğin 1 = 3 ifadesi gibi.
Örneğin şu denklemler
tutarsızdır. Bir çözüm bulmaya çalışmak için, söylenmeden anlaşılan "bir çözüm vardır" varsayımını yapmaktayız. Diğer bir ifade ile, birinci denklemmde bulunan 


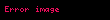

Üç doğrusal denklemli dizgede, bu dizgedeki herhangi iki denklem birlirleriyle tutarlı olmalarıyla beraber, denklemlerin tutarsız olmaları mümkündür. Örneğin şu denklemler tutarsızdır:
Birinci ile ikinci denklemin birbiriyle toplamaları ile
elde edilir ve bu üçüncü denkelmeden çıkartılırsa sonuç
0 = 1
olur. Dikkat edilirse bu denklemlerden herhangi bir iki denklemli dizgenin bir ortak çözümü vardır. Aynı olgu her türlü sayıda denkelemler dizgesinde de oluşabilir.
Genel bir sonuç olarak, eğer bir doğrusal denklemler dizgesindeki denklemlerin sol tarafındaki ifadeler doğrusal olarak bağımlı olursa ve sabit terimler bağımlılık bağlantısını tatmin etmiyorlarsa, tutarsızlık ortaya çıkar. Eğer bir doğrusal denklemler dizgesinin sol tarafındaki ifadeler doğrusal olarak bağımsızlarsa, bu dizge her zaman tutarlı olur.
Denklik
Aynı değişkenleri kullanan iki değişik doğrusal denklemler dizgesinin birbirleriye denk olması için ikinci dizgede bulunan denklemlerin her birinin, birinci dizgede bulunan denklemlerden cebir kullanılarak hesaplanıp elde edilebilmesi gerekir ve bunun aksinin de doğru olması gereklidir. Birbirine denk dizgeler değişken değerleri hakkında birbirine tıpatıp aynı bilgileri vermektedirler. Özellikle, eğer iki dizgenin tıpatıp aynı çözüm kümesi bulunuyorsa iki doğrusal denklemler dizgesi birbirlerine denktirler.
Doğrusal denklemler dizgesinin çözümü
Bir doğrusal denklem dizgesini çözümlemek için birkaç değişik algoritması bulunur.
Çözümü tanımlama
Eğer çözüm kümesi sonsuz değilse, genellikle bu küme olarak ve küme notasyonu kullanarak ifade edilir. Örneğin 2, 3, 4 olan çözüm kümesi 
Eğer sonsuz sayıda çözüm bulunuyorsa bunu küme olarak ve küme notasyonu kullanarak ifade etmek çok güç olur. Tipik olarak değişkenlerden bazıları bağımsız (veya özgür veya parametre) olarak kabul edilirler ve herhangi bir değer alabilirler. Geride kalan değişkenler bağımsız değişkenlerin değerlerine bağlı olurlar.
Örneğin şu dizgeye ele alalım:
Bu dizge için çözüm kümesi şu denklemeler ile ifade edilebilir:
Burada 






Her bir bağımsız değişken çözüm kümesine bir serbestlik derecesi verir ve serbestlik derecesi sayısı çözüm kümesinin boyutuna eşittir. Örneğin, yukarıda verilen denklemin çözüm kümesi bir doğru olur; çünkü çözüm kümesi üzerinde bulunan tek bir nokta 
Bağımsız değişkenler için değişik seçim değerleri, aynı çözüm kümesinin değişik tanımlarını oratay çıkarabilir. Örneğin yukarıda verilen denklemlerin çözümü alternatif olarak şöyle değişik şekilde tanımlanabilir:
Burada 


Değişkenlerin arka arkaya eliminasyonu
Bir doğrusal denklemler dizgesine çözüm kümesi bulmak için en basit yöntem değişkenlerin tekere teker arkaarkaya elimine edilmesidir. Bu çözüm yöntemi şöyle tanımlanabilir:
- Birinci denklemdeki tek bir değişkeni (eşit işaretinin solunda) diğer değişkenler ve sabitle (sağda) ifade edilmesini sağlayınız.
- Bu değişken için birinci denkelmeden bulunan ifadeyi dizgenin diğer denklemelerinde bulunan ifadeleri içindeki o değişken yerine konulur ve böylece yeni bir denklemler dizgesi bulunur ve bu dizgede bir önce dizgeden bir değişken eksik olur.
- Bu yeni dizgeye aynı yöntemi uygulayınız, Böylece tekrar bir değişken eksik yeni bir dizge bulunuz.
- Bu yöntemi arkaarkaya uygulayınız ve son bulunan dizge tek bir doğrusal denklem olana kadar bir yöntemi uygulamaya devam ediniz.
- Bu son tek değişkenli denklemi çözünüz ve bu son değişkenin çözüm değerini bulunuz.
- Bu değeri diğer bir öneceki dizgede geriye koyup bir diğer değişkenin çözüm değerini bulun. Bu geriye koyup çözmeyi tüm değişkenler için çözüm bulana kadar tekrarlayınız.
Örneğin şu 3 değişkenli (x, y ve z) doğrusal denklemeler dizgesini ele alalım :
Birinci deklemi x için çözelim ve şu ifadeyi elde ederiz;
x = 5 + 2z − 3y
Bu x için ifadeyi ikinci ve üçüncü doğrusal denkleme koyup bunları basitleştirelim ve şu iki değişkenli (y ve z) iki denklem bulunuruz:
Bu yeni iki değişkenli iki denklemli dizgenin birinci denklemini y için çözelim ve şu ifadeyi elde ederiz
y = 2 + 3z,
Bunu yeni dizgedeki ikinci denkleme koyalım. y için çözünce şu ifade elde edilir:
y = 2 + 3z
Bunu ikinci denkleme y için koyarsak
z = 2
ifadesini elde ederiz. Şimdi sadece z ifadeli tek doğrusal denklem dizge elimizde kalmıştır ve bu da z için şu çözümü verir:
z = 2
Arkaarkaya tek değişken eliminasyonu ile sonuçlar bulmuştuk:
Şimdi z = 2 çözümünü ikinci denkelem koyarsak y çözümü olarak y = 8
elde ederiz; ve z = 2 ile y = 8 çözümlerini birinci denkleme koyarsak
x = −15
olarak x çözümü bulunur.
Böylece, çözüm kümesi olarak tek bir nokta olan (x, y, z) = (−15, 8, 2) elde edilmiş olmaktadır.
Sıra azaltma
a_ij katsayıları rasyonel sayılar, gercek sayılar ya da karmasik sayılar ya da herhangi bir cisimden gelen sayılar olmak üzere
a_11 x_1 + a_12 x_2 + ... + a_1n x_n = b_1
a_m1 x_1 + a_m2 x_2 + ... + a_mn x_n = b_m denklem sistemi,
A m satir ve n sutundan olusan ve değerlerini (bir cisimden alan) bir matris, x n satirlik bir sutun vektoru, b (değerlerini ayni cisimden alan) m satirlik bir sutun vektoru olmak üzere
Ax = b
seklinde yazabiliriz.
Boyle bir sistemin çözümü, x_i degiskenlerinin hangi degerlerinin denklem sistemini sağladığını bulmak anlamina gelmektedir.
Gauss tipi indirgemede temel indirgeme islemleri uygulanir.
Temel satir indirgeme islemleri aşağıdakilerdir. Dikkat edelim ki bu islemler denklem sisteminin çözüm kumesini degistirmezler.
Satir Ekleme i. satirin herhangi k katini j. satira eklemek. Bu islemi k * Satir_i + Satir_j -> Satir_j ya da Satir (k*i+j->j) ile gösterelim.
Not: bu islem A matrisini, I+ kE_ji matrisi ile soldan carpmaya karsilik gelmektedir. Burada I kosegen terimleri 1 olan m * m boyutundaki matrisi, E_ji, sadece j. satir ve i. sutundaki terimi 1 olan matrisi göstermektedir. Boylece incelenen doğrusal sistem Ax = b yerine (I+kE_ji)A x = (I+kE_ji)b doğrusal sistemi olmaktadır.
Satir Degistirme i. satirla j. satiri yer degistirmek. Bu islemi Degistir (i,j) ile gösterelim.
Bu islem i ve j indeksleri haric diğer indekslerde sadece kosegen terimleri 1, diğer durumlarda (i,j) ve (j,i) terimleri 1 olan matris ile A matrisini soldan carpmak ile elde edilir. Boylece incelenen doğrusal sistem Ax = b yerine (I-E_ii-E_jj+E_ij+E_ji)A x = (I-E_ii-E_jj+E_ij+E_ji)b doğrusal sistemi olmaktadır.
Gauss-Jordan Indirgeme yöntemi:
Serbest degisken kavrami: Eger ilk sutun (ya da herhangi bir j. sutun) sadece sifirlardan olusuyorsa o zaman ilk degisken (ya da j. degisken) aslında denklem sistemi tarafından kısıtlanmamaktadır. Yani bu degiskenin herhangi bir degeri alabilir. Herhangi degeri alabilen degiskenlere serbest degisken denir.
Sifir olmayan ilk sutundan baslamak üzere (bu sutun j_1. sutun olsun) 1. j_1. sutundaki ilk sifirdan farklı sayınn bulunduğu satiri (bu satir i_1. satir olsun) ilk satirla degistir. Bu adimdan sonra olusan matrisin 1. satir ve j1. sutunundaki sifirdan farklı sayı A olsun. (Matristeki bu tip terimlere pivot ya da eksen terimleri denir. Cozumler bu Ikinci satirdan baslamak üzere j1. sutunda sifir olmayan ilk terim B olsun ve bu terim i_2. satirda yer alsin. 2. Ilk satirin (-B/A) katini i_2. satira ekle. Boylece i_2. satirin j_1. terimi sifira donusecektir. 3. Bu islemi bitirdikten sonra j_1. sutunda hala incelenmemis satir varken bir sonraki satira gecerek 2. adimi tekrarla. 4. j_1. sutundaki islem bittikten sonra yukaridaki adımları degistirilmis A matrisinin j1 den büyük sutunları ve 1den büyük satırlarından olusan matrise uygula. (Bundan sonraki adimda A matrisi yerine A >= j1, >=1 matrisine uygula.)
Bu işlemlerin sonunda (j_1,1) (j_2,2) (j_k,k) pivot konumları olsun. En son sifirdan farklı satirdan baslayip yukari cikarak doğrusal sistemin çözümune ulasabiliriz. Islemleri kolaylastirmak için j_v. sutunda v degerinden kucuk satirlardaki sifirdan farklı terimleri yukaridaki 2. adimdaki islemi kullanarak indirgeyebiliriz. Ayrica pivot degerlerin 1 olmasi kosulunu da ekleyerek, bu çözüm yöntemine degisiklikler yapabiliriz.
Cramer kuralı
Bu kural 1750'de "Introduction à l'analyse des lignes courbes algébriques (Cebirsel eğrilerinin analizine giriş)" adlı eserinde bu teoremi açıklayan Gabriel Cramer (1704–1752) anısına isimlendirilmiştir.
Cramer kuralı aynı sayıda değişken ile denklem bulunan doğrusal denklem dizgesinin çözüm kümesini bulmak için kullanılabilen bir ifade ortaya çıkaran bir doğrusal cebir teoremidir. Bu teorem kullanılarak çözüm tek ve tek bir çözüm kümesi bulunan doğrusal denklem dizgesi için geçerlidir. Bu halde her bir değişken için çözüm iki kare determinantın oranı olarak verilir; bu oranda pay katsayılar matrisinden o değişkene karşıt sütununun, denklemin sağ-tarafında olan sabitler vektörü ile ikame edilmesiyle elde edilen kare matrisin determinantı ve payda ise katsayılar kare matrisi determinantıdır.
Genel olarak açıklamak için aynı sayıda (n) değişkenli ve denklemli bir doğrusal denklemler dizgesinin şu matris ifadesini ele alalım:
| | 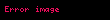 |
Burada 



Burada 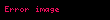


İki değişkenli iki doğrusal denklemli dizge örneği
Bu örnekte, determinantların içinde hangi elemanlar bulunduğunun hemen anlaşılması içcin, katsayılar 


Üç değişkenli üç doğrusal denklemli dizge örneği
Diğer yöntemler
Homojen dizgeler
Tanımlama
Bir doğrusal denklemler dizgesinde sabitlerin hepsi 0 iselr, bu doğrsusal denklemler dizgesi homojen dizge olarak tanımlanır:
Matris ifadesiyle bir genel homojen dizge şöyle ifade edilir:
Burada
A: (mxn) düzenli katsayılar matrisi;
x: (n)-sıralı değişkenler vektörü veya sütun-matrisi ve ;
0: (m)-siralı veya 0 girdili sütun-matris ;
olur.
Çözüm kümesi
Her homojen dizgenin en aşağı bir tane çözümü vardır; bu her değişkenin 0'a eşit olduğu çözüm kümesidir. Bu çözüme sıfır çözümü veya önemsiz (trivial) çözüm adı verilir.
Homoojen dizgelerin önemli olan şu diğer nitelikleri de bulunur:
- Eğer u ve v homojen dizgenin iki çözüm vektörü iseler;

vektörler toplamı da homojen dizgenin bir çözümü olur.
- Eğer u bir homojen dizgenin bir çözümünü ifade etmekte ise ve z herhangi bir skaler değer ise; o zaman
vektör çarpımı da homojen dizgenin bir çözümüdür.
Bu çözüm kümesi nitelikleri, R<sup>n</sup> nin bir Euclid-tipi altuzayı için gerekli nitelikler ile tıpatıp aynıdır. Özellikle, bir homojen dizgenin çözüm kümesi buna tekabül eden A matrisinin ile aynıdır.
Homojen olmayan dizgelerle ilişkiler
Kaynakça
- İngilizce Wikipedia "System of linear equations" maddesi 5 Mart 2011 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
Ayrıca bakınız
Dış bağlantılar
- İTÜ Ninova Açık Ders Malzemeleri[], Doğrusal cebir
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dogrusal denklem dizgesi birkac tane ayni tip degiskenleri iceren birkac tane dogrusal denklemlerin olusturdugu topluluktur Ornegin Uc bilinmeyenli ve uc dogrusal denklemli bir dogrusal denklem dizgesi geometrik olarak uc boyutta uc duzeyin kesismesi seklinde gorulur Eger bir cozum bulunuyorsa bu cozum uc duzeyin kesisme noktasindadir 3x1 2x2 x3 12x1 2x2 4x3 2 x1 12x2 x3 0 displaystyle left begin array rcrcrcr 3 x 1 amp amp 2 x 2 amp amp x 3 amp amp 1 2 x 1 amp amp 2 x 2 amp amp 4 x 3 amp amp 2 x 1 amp amp frac 1 2 x 2 amp amp x 3 amp amp 0 end array right Burada uc cesit degisken x1 displaystyle x 1 x2 displaystyle x 2 ile x3 displaystyle x 3 bulunur ve bu uc degisken uc ayri dogrusal denklem icindedir ve boylece dogrusal denklemler sistemi dizge elde edilir Bir dogrusal dizgenin cozumu bilinmeyen degiskenlere tum dogrusal denklemleri ayni zamanda tatmin eden reel sayilarin tahsis edilmesidir Yukaridaki denklemler dizgesi icin cozum kumesi bulunur ve bu x1 1x2 2x3 2 displaystyle begin alignedat 2 x 1 amp amp 1 x 2 amp amp 2 x 3 amp amp 2 end alignedat olur Dogrusal denklem dizgeleri muhendislik fizik kimya bilgisayar bilimi ve ekonomide pek cok uygulama alani bulur Genel sekiln bilinmeyen degiskenli m sayida dogrusal denklemden olusan bir dogrusal denklen dizgesi genel olarak soyle yazilabilir a11x1 a12x2 a1nxn b1a21x1 a22x2 a2nxn b2 am1x1 am2x2 amnxn bm displaystyle begin matrix a 11 x 1 amp a 12 x 2 amp dots amp a 1n x n amp b 1 a 21 x 1 amp a 22 x 2 amp dots amp a 2n x n amp b 2 dots amp dots amp dots amp dots amp dots a m1 x 1 amp a m2 x 2 amp dots amp a mn x n amp b m end matrix Burada x1 x2 xn displaystyle x 1 x 2 x n n tane bilinmeyen degiskendir a11 a12 amn displaystyle a 11 a 12 a mn bu degiskenlerin katsayilaridir Her katsayinin altinda bulunan ilk sayi denklem sayisina ve ikincisi degisken tipinin sayisina tekabul eder ornegin a 31 displaystyle a 31 ucuncu denklemdeki birinci degisken x1 displaystyle x 1 in katsayisidir b1 b2 bm displaystyle b 1 b 2 b m terimleri ise her denklem icin sabit terimleri verir Cok kere katsayilar ve bilinmeyen degiskenler reel sayilardir Fakat ileri matematikte bunlar karmasik sayilar tam sayilar polinomlar ve hatta soyut cebirsel yapilar bile olabilirler Vektor denklemi Bu genel dogrusal denklemler dizgesini uygun bir sekilde ifade edilmesi vektorler halinde olur Bu ifade seklinde her bir degisken bir bir agirlik olarak bir sutun vektor ile ifade edilmektedir x1 a11a21 am1 x2 a12a22 am2 xn a1na2n amn b1b2 bm displaystyle x 1 begin bmatrix a 11 a 21 vdots a m1 end bmatrix x 2 begin bmatrix a 12 a 22 vdots a m2 end bmatrix cdots x n begin bmatrix a 1n a 2n vdots a mn end bmatrix begin bmatrix b 1 b 2 vdots b m end bmatrix Matris denklemi Vektor denklemine aynen tekabul eden ve matriks kullanilarak ifade edilen genel dogrusal denklemler dizgesi su sekilde ifade edilir Ax b displaystyle A mathbf x mathbf b burada A m n matrisi x icinde n tane ifade bulunan bir ve b icinde m tane sabit ifade olan bir sutun vektoru olur A a11a12 a1na21a22 a2n am1am2 amn x x1x2 xn b b1b2 bm displaystyle A begin bmatrix a 11 amp a 12 amp cdots amp a 1n a 21 amp a 22 amp cdots amp a 2n vdots amp vdots amp ddots amp vdots a m1 amp a m2 amp cdots amp a mn end bmatrix quad mathbf x begin bmatrix x 1 x 2 vdots x n end bmatrix quad mathbf b begin bmatrix b 1 b 2 vdots b m end bmatrix Cozum kumesix y 1 ve 3x y 9 denklemleri icin cozum kumesi tek bir noktada 2 3 olur Bir dogrusal denklem dizgenin cozumu bilinmeyen degiskenlere yani x1 x2 xn degiskenlerine tum dogrusal denklemleri ayni zamanda tatmin eden reel sayisal degerler tahsis edilmesidir Tum mumkun cozumlerin bir matematiksel kumesine cozum kumesi adi verilir Bir dogrusal denklem dizgesi icin uc ve sadece alternatif mumkun sonuc ortaya cikabilir Sistemin sonsuz sayida cesitli cozumu bulunur Sistemin tek bir cozumu bulunur Sistemin hicbir cozumu bulunmaz Geometrik yorum Iki degiskenden x1 displaystyle x 1 ve x2 displaystyle x 2 olusan bir dizge icin her bir denklem x1 displaystyle x 1 ve x2 displaystyle x 2 eksenli dikdortgen koordinat sistemi grafigi icinde bir ile gosterilir Bir cozum dizgedeki tum denklemleri tatmin etmesi gerektigi icin cozum kumesi bu dogrularin kesisme noktasidir veya tek bir dogru ya tek bir nokta ya da bos kume olarak gorulur Uc degiskenli bir dizge icin her dogrusal denklem uc boyutlu bir uzayda bir olurlar ve cozum kumesi bu duzlemlerin kesismesidir Boylece cozum kumesi ya bir duzlem ya tek bir dogru ya tek bir nokta ya da bos kume olur n sayida degisken halinde her bir dogrusal denklem bir bir olarak ortaya cikar Cozum kumesi bu hiperduzlemlerin kesismeleridir ve n ye kadar herhangi bir boyutta olabilir Genel sonuc hali Uc degiskenli iki denklemden olusan bir dizgenin cozumu genellikle bir dogrudur Genel olarak bir dogrusal denklemler dizgesinin sonucunun ne olabilecegi denklemler sayisi ile bilinmeyen degiskenler sayisi arasindaki baglantilar tarafindan belirlenir Genellikle eger dizgede denklem sayisi bilinmeyen degisken sayisindan daha kucukse ise dizge icin sonsuz sayida cozum bulunur Fakat bazen tek bir seyrek cozum bulma imkani da vardir Yani kullandigimiz notasyona gore m lt n ise sonsuz cozum vardir Bu cesit dizgelere kararsiz dizge underdetermined system adi verilir Genellikle eger dizgede denklem sayisi degisken sayisi ile ayni ise tek bir tane cozum bulunur yani m n ise tek ve tek bir cozum bulunur Genellikle eger dizgede denklem sayisi degisken sayisidan daha buyuk ise hicbir scozum bulunmaz yani m gt n ise hicbir cozum bulunmaz Asagidaki gosterimler iki degiskenli halde ortaya cikabilmesi mumkun uclu sonucu gostermektedir Bir Denklem Iki Denklem Uc Denklem Verilen gosterimede birinci dizgenin sonsuz sayida cozumu bulunur yani bunun noktalari mavi renkli dogru uzerindedir Ikinci dizgede tek bir cozum bulunur yani iki dogrunun kesisme noktasi cozumdur Ucuncu sistemde bulunan uc dogrunun ortaklasa hicbir noktalari bulunmaz Fakat sunu unutmamak gerekir butun bu sonuclar sadece genellikle dogrudur Iki denklemeli ve iki degiskenli bir dizgenin hicbir cozumu olmamasi mumkundur bu hal her iki dogru birbirine paralel ise ortaya cikar Uc denklemle iki degiskenli bir dizgenin cozumu olmasi mumkundur bu hal eger uc dogru birbiriyle tek noktada kesisirlerse ortaya cikar Genel olarak bir dogrusal denklemler dizgesi beklenenden degisik davranis gostermesi eger denklemler dogrusal olarak bagimli iseler veya iki veya daha cok sayida denklemlerin tutarsiz olmalari halinde ortaya cikar NiteliklerBagimsizlik Bir dogrusal denklem dizgesinin denklemleri bagimsizlik niteligi dizgede bulunan denklem esitliklerinin hicbiri denklemden cebirsel olarak cikartilamasi halidir Eger denklemler bagimsizlarsa her bir denklem degiskenler hakkinda yeni bilgi kapsamaktadir ve bu denklemlerden herhangi birinin ortadan kaldirilmasi cozum kumesinin boyutunu artir Dogrusal denklemler icin mantiksal bagimsizlik ozelligiyle ile aynidir x1 2x2 1 displaystyle x 1 2x 2 1 3x1 5x2 8 displaystyle 3x 1 5x 2 8 ve 4x1 3x2 7 displaystyle 4x 1 3x 2 7 denklemleri dogrusal olarak bagimsiz degildirler Ornegin su denklemler 3x1 2x2 6ve6x1 4x2 12 displaystyle 3x 1 2x 2 6 text ve 6x 1 4x 2 12 bagimsiz degildirler cunku ikinci denklem birinci denklemin 2 ile carpimi ile elde edilmistir ve eger bu iki denklem icin grafik cizilirse iki dogru uste cakisip tek bir dogru goruntusu verirler Daha karmasik bir ornek icin verilen denklemler dizgesi su olsun x1 2x2 13x1 5x2 84x1 3x2 7 displaystyle begin alignedat 5 x 1 amp amp amp amp 2x 2 amp amp amp amp 1 amp 3x 1 amp amp amp amp 5x 2 amp amp amp amp 8 amp 4x 1 amp amp amp amp 3x 2 amp amp amp amp 7 amp end alignedat Bu uc denklem dizgesi bagimsiz degildir cunku ucuncu denklem ilk iki denklemin birbirine toplamindan elde edilmistir Gercekten bu uc denklemden herhangi ikisinden ucuncu denklem cikartilabilir ve bu uc denklemden herhangi tek bir tanesi ortadan kaldirilirsa cozum kumesi hic degismeden ayni kalir Bu uc dogru icin grafik ucu de tek bir noktada kesisen uc dogru seklindedir Tutarlilik Bir dogrusal denklemler dizgesi denklemleri eger bir ortak cozum varsa tutarli olur aksi halde tutarsiz olur Eger denklemler tutarli iseler denklemlerden bir ortaya cikartmak imkani bulunur ornegin 1 3 ifadesi gibi Ornegin su denklemler 3x1 2x2 6 ve 3x1 2x2 12 displaystyle 3x 1 2x 2 6 text ve 3x 1 2x 2 12 tutarsizdir Bir cozum bulmaya calismak icin soylenmeden anlasilan bir cozum vardir varsayimini yapmaktayiz Diger bir ifade ile birinci denklemmde bulunan x1 displaystyle x 1 degerinin ikinci denklemde bulunan x1 displaystyle x 1 degeri ile ayni acikca oldugunu acikca soylemeden varsaymaktayiz ve ayni sekilde ve ayni zamanda her iki denklemde de x2 displaystyle x 2 ayni varsayimi yapiyoruz 3x1 2x2 displaystyle 3x 1 2x 2 icin ikame ediliebilirlik ozelligini uyguluyarak 6 12 olarak bir denklem buluruz ve bu da yanlis bir ifadededir Bu hatali ifade dizgenin bir cozumu olduguna dair yaptimiz varsayim ile celismektedir ve bundan dolayi varsayimimizin yanlis oldugu sonucu cikmaktadir yani dogrusal denklemler dizgesinin hicbir cozumu bulunmaz Bu denklemlerin x1x2 displaystyle x 1 x 2 duzeyindeki grafikleri birbirine parallel iki dogru halindedir Uc dogrusal denklemli dizgede bu dizgedeki herhangi iki denklem birlirleriyle tutarli olmalariyla beraber denklemlerin tutarsiz olmalari mumkundur Ornegin su denklemler tutarsizdir x1 x2 12x1 x2 13x1 2x2 3 displaystyle begin alignedat 7 x 1 amp amp amp amp x 2 amp amp amp amp 1 amp 2x 1 amp amp amp amp x 2 amp amp amp amp 1 amp 3x 1 amp amp amp amp 2x 2 amp amp amp amp 3 amp end alignedat Birinci ile ikinci denklemin birbiriyle toplamalari ile 3x1 2x2 2 displaystyle 3x 1 2x 2 2 elde edilir ve bu ucuncu denkelmeden cikartilirsa sonuc 0 1 olur Dikkat edilirse bu denklemlerden herhangi bir iki denklemli dizgenin bir ortak cozumu vardir Ayni olgu her turlu sayida denkelemler dizgesinde de olusabilir Genel bir sonuc olarak eger bir dogrusal denklemler dizgesindeki denklemlerin sol tarafindaki ifadeler dogrusal olarak bagimli olursa ve sabit terimler bagimlilik baglantisini tatmin etmiyorlarsa tutarsizlik ortaya cikar Eger bir dogrusal denklemler dizgesinin sol tarafindaki ifadeler dogrusal olarak bagimsizlarsa bu dizge her zaman tutarli olur Denklik Ayni degiskenleri kullanan iki degisik dogrusal denklemler dizgesinin birbirleriye denk olmasi icin ikinci dizgede bulunan denklemlerin her birinin birinci dizgede bulunan denklemlerden cebir kullanilarak hesaplanip elde edilebilmesi gerekir ve bunun aksinin de dogru olmasi gereklidir Birbirine denk dizgeler degisken degerleri hakkinda birbirine tipatip ayni bilgileri vermektedirler Ozellikle eger iki dizgenin tipatip ayni cozum kumesi bulunuyorsa iki dogrusal denklemler dizgesi birbirlerine denktirler Dogrusal denklemler dizgesinin cozumuBir dogrusal denklem dizgesini cozumlemek icin birkac degisik algoritmasi bulunur Cozumu tanimlama Eger cozum kumesi sonsuz degilse genellikle bu kume olarak ve kume notasyonu kullanarak ifade edilir Ornegin 2 3 4 olan cozum kumesi 2 3 4 displaystyle 2 3 4 olarak yazilir Eger sonsuz sayida cozum bulunuyorsa bunu kume olarak ve kume notasyonu kullanarak ifade etmek cok guc olur Tipik olarak degiskenlerden bazilari bagimsiz veya ozgur veya parametre olarak kabul edilirler ve herhangi bir deger alabilirler Geride kalan degiskenler bagimsiz degiskenlerin degerlerine bagli olurlar Ornegin su dizgeye ele alalim x1 3x2 2x3 53x1 5x2 6x3 7 displaystyle begin alignedat 7 x 1 amp amp amp amp 3x 2 amp amp amp amp 2x 3 amp amp amp amp 5 amp 3x 1 amp amp amp amp 5x 2 amp amp amp amp 6x 3 amp amp amp amp 7 amp end alignedat Bu dizge icin cozum kumesi su denklemeler ile ifade edilebilir x1 7x3 1 ve x2 3x3 2 displaystyle x 1 7x 3 1 text ve x 2 3x 3 2 text Burada x3 displaystyle x 3 bagimsiz degiskendir x1 displaystyle x 1 ve x2 displaystyle x 2 degiskenleri x3 displaystyle x 3 ye baglidirlar Cozum kumesinde bulunan herhangi nokta once x3 displaystyle x 3 icin herhangi bir deger secmekle ve sonra da x1 displaystyle x 1 ve x2 displaystyle x 2 icin bu secilen degere tekabul eden degerleri hesaplama seklinde ortaya cikartilir Her bir bagimsiz degisken cozum kumesine bir serbestlik derecesi verir ve serbestlik derecesi sayisi cozum kumesinin boyutuna esittir Ornegin yukarida verilen denklemin cozum kumesi bir dogru olur cunku cozum kumesi uzerinde bulunan tek bir nokta x3 displaystyle x 3 parametre degiskenin degerini sahsi secime bagli olarak belirlemek suretiyle ortaya cikartilir Daha yuksek duzenli sonsuz sayida cozum bir duzlemi veya yuksek boyutlu hiperduzlemi tanimlayabilir Bagimsiz degiskenler icin degisik secim degerleri ayni cozum kumesinin degisik tanimlarini oratay cikarabilir Ornegin yukarida verilen denklemlerin cozumu alternatif olarak soyle degisik sekilde tanimlanabilir x2 37x1 117 ve x3 17x1 17 displaystyle x 2 frac 3 7 x 1 frac 11 7 text ve x 3 frac 1 7 x 1 frac 1 7 text Burada x1 displaystyle x 1 bagimsiz degisken ve x2 displaystyle x 2 ve x3 displaystyle x 3 bagli degiskenlerdir Degiskenlerin arka arkaya eliminasyonu Bir dogrusal denklemler dizgesine cozum kumesi bulmak icin en basit yontem degiskenlerin tekere teker arkaarkaya elimine edilmesidir Bu cozum yontemi soyle tanimlanabilir Birinci denklemdeki tek bir degiskeni esit isaretinin solunda diger degiskenler ve sabitle sagda ifade edilmesini saglayiniz Bu degisken icin birinci denkelmeden bulunan ifadeyi dizgenin diger denklemelerinde bulunan ifadeleri icindeki o degisken yerine konulur ve boylece yeni bir denklemler dizgesi bulunur ve bu dizgede bir once dizgeden bir degisken eksik olur Bu yeni dizgeye ayni yontemi uygulayiniz Boylece tekrar bir degisken eksik yeni bir dizge bulunuz Bu yontemi arkaarkaya uygulayiniz ve son bulunan dizge tek bir dogrusal denklem olana kadar bir yontemi uygulamaya devam ediniz Bu son tek degiskenli denklemi cozunuz ve bu son degiskenin cozum degerini bulunuz Bu degeri diger bir oneceki dizgede geriye koyup bir diger degiskenin cozum degerini bulun Bu geriye koyup cozmeyi tum degiskenler icin cozum bulana kadar tekrarlayiniz Ornegin su 3 degiskenli x y ve z dogrusal denklemeler dizgesini ele alalim x 3y 2z 53x 5y 6z 72x 4y 3z 8 displaystyle begin alignedat 7 x amp amp amp amp 3y amp amp amp amp 2z amp amp amp amp 5 amp 3x amp amp amp amp 5y amp amp amp amp 6z amp amp amp amp 7 amp 2x amp amp amp amp 4y amp amp amp amp 3z amp amp amp amp 8 amp end alignedat Birinci deklemi x icin cozelim ve su ifadeyi elde ederiz x 5 2z 3y Bu x icin ifadeyi ikinci ve ucuncu dogrusal denkleme koyup bunlari basitlestirelim ve su iki degiskenli y ve z iki denklem bulunuruz 4y 12z 8 2y 7z 2 displaystyle begin alignedat 5 4y amp amp amp amp 12z amp amp amp amp 8 amp 2y amp amp amp amp 7z amp amp amp amp 2 amp end alignedat Bu yeni iki degiskenli iki denklemli dizgenin birinci denklemini y icin cozelim ve su ifadeyi elde ederiz y 2 3z Bunu yeni dizgedeki ikinci denkleme koyalim y icin cozunce su ifade elde edilir y 2 3z Bunu ikinci denkleme y icin koyarsak z 2 ifadesini elde ederiz Simdi sadece z ifadeli tek dogrusal denklem dizge elimizde kalmistir ve bu da z icin su cozumu verir z 2 Arkaarkaya tek degisken eliminasyonu ile sonuclar bulmustuk x 5 2z 3yy 2 3zz 2 displaystyle begin alignedat 7 x amp amp amp amp 5 amp amp amp amp 2z amp amp amp amp 3y amp y amp amp amp amp 2 amp amp amp amp 3z amp amp amp amp amp z amp amp amp amp 2 amp amp amp amp amp amp amp amp amp end alignedat Simdi z 2 cozumunu ikinci denkelem koyarsak y cozumu olarak y 8 elde ederiz ve z 2 ile y 8 cozumlerini birinci denkleme koyarsak x 15 olarak x cozumu bulunur Boylece cozum kumesi olarak tek bir nokta olan x y z 15 8 2 elde edilmis olmaktadir Sira azaltma a ij katsayilari rasyonel sayilar gercek sayilar ya da karmasik sayilar ya da herhangi bir cisimden gelen sayilar olmak uzere a 11 x 1 a 12 x 2 a 1n x n b 1 a m1 x 1 a m2 x 2 a mn x n b m denklem sistemi A m satir ve n sutundan olusan ve degerlerini bir cisimden alan bir matris x n satirlik bir sutun vektoru b degerlerini ayni cisimden alan m satirlik bir sutun vektoru olmak uzere Ax b seklinde yazabiliriz Boyle bir sistemin cozumu x i degiskenlerinin hangi degerlerinin denklem sistemini sagladigini bulmak anlamina gelmektedir Gauss tipi indirgemede temel indirgeme islemleri uygulanir Temel satir indirgeme islemleri asagidakilerdir Dikkat edelim ki bu islemler denklem sisteminin cozum kumesini degistirmezler Satir Ekleme i satirin herhangi k katini j satira eklemek Bu islemi k Satir i Satir j gt Satir j ya da Satir k i j gt j ile gosterelim Not bu islem A matrisini I kE ji matrisi ile soldan carpmaya karsilik gelmektedir Burada I kosegen terimleri 1 olan m m boyutundaki matrisi E ji sadece j satir ve i sutundaki terimi 1 olan matrisi gostermektedir Boylece incelenen dogrusal sistem Ax b yerine I kE ji A x I kE ji b dogrusal sistemi olmaktadir Satir Degistirme i satirla j satiri yer degistirmek Bu islemi Degistir i j ile gosterelim Bu islem i ve j indeksleri haric diger indekslerde sadece kosegen terimleri 1 diger durumlarda i j ve j i terimleri 1 olan matris ile A matrisini soldan carpmak ile elde edilir Boylece incelenen dogrusal sistem Ax b yerine I E ii E jj E ij E ji A x I E ii E jj E ij E ji b dogrusal sistemi olmaktadir Gauss Jordan Indirgeme yontemi Serbest degisken kavrami Eger ilk sutun ya da herhangi bir j sutun sadece sifirlardan olusuyorsa o zaman ilk degisken ya da j degisken aslinda denklem sistemi tarafindan kisitlanmamaktadir Yani bu degiskenin herhangi bir degeri alabilir Herhangi degeri alabilen degiskenlere serbest degisken denir Sifir olmayan ilk sutundan baslamak uzere bu sutun j 1 sutun olsun 1 j 1 sutundaki ilk sifirdan farkli sayinn bulundugu satiri bu satir i 1 satir olsun ilk satirla degistir Bu adimdan sonra olusan matrisin 1 satir ve j1 sutunundaki sifirdan farkli sayi A olsun Matristeki bu tip terimlere pivot ya da eksen terimleri denir Cozumler bu Ikinci satirdan baslamak uzere j1 sutunda sifir olmayan ilk terim B olsun ve bu terim i 2 satirda yer alsin 2 Ilk satirin B A katini i 2 satira ekle Boylece i 2 satirin j 1 terimi sifira donusecektir 3 Bu islemi bitirdikten sonra j 1 sutunda hala incelenmemis satir varken bir sonraki satira gecerek 2 adimi tekrarla 4 j 1 sutundaki islem bittikten sonra yukaridaki adimlari degistirilmis A matrisinin j1 den buyuk sutunlari ve 1den buyuk satirlarindan olusan matrise uygula Bundan sonraki adimda A matrisi yerine A gt j1 gt 1 matrisine uygula Bu islemlerin sonunda j 1 1 j 2 2 j k k pivot konumlari olsun En son sifirdan farkli satirdan baslayip yukari cikarak dogrusal sistemin cozumune ulasabiliriz Islemleri kolaylastirmak icin j v sutunda v degerinden kucuk satirlardaki sifirdan farkli terimleri yukaridaki 2 adimdaki islemi kullanarak indirgeyebiliriz Ayrica pivot degerlerin 1 olmasi kosulunu da ekleyerek bu cozum yontemine degisiklikler yapabiliriz Cramer kurali Bu kural 1750 de Introduction a l analyse des lignes courbes algebriques Cebirsel egrilerinin analizine giris adli eserinde bu teoremi aciklayan Gabriel Cramer 1704 1752 anisina isimlendirilmistir Cramer kurali ayni sayida degisken ile denklem bulunan dogrusal denklem dizgesinin cozum kumesini bulmak icin kullanilabilen bir ifade ortaya cikaran bir dogrusal cebir teoremidir Bu teorem kullanilarak cozum tek ve tek bir cozum kumesi bulunan dogrusal denklem dizgesi icin gecerlidir Bu halde her bir degisken icin cozum iki kare determinantin orani olarak verilir bu oranda pay katsayilar matrisinden o degiskene karsit sutununun denklemin sag tarafinda olan sabitler vektoru ile ikame edilmesiyle elde edilen kare matrisin determinanti ve payda ise katsayilar kare matrisi determinantidir Genel olarak aciklamak icin ayni sayida n degiskenli ve denklemli bir dogrusal denklemler dizgesinin su matris ifadesini ele alalim Ax b displaystyle Ax b 1 displaystyle 1 Burada A displaystyle A matrisi nxn seviyeli sonsuz degeri olmayan bir determinanti bulunan bir katsayilar kare matrisi x x1 xn displaystyle x x 1 ldots x n top nx1 seviyeli bir degiskenler sutun vektoru ve b b1 bn displaystyle b b 1 ldots b n top ise nx1 seviyeli bir sabitler sutun vektoru olur xi displaystyle x i degiskeni cozumu icin Cramer Teoremi soyle ifade edilir xi det Ai det A i 1 n displaystyle x i frac det A i det A qquad i 1 ldots n Burada Ai displaystyle A i matrisi A displaystyle A kare matrisinin i inci sutununun yerine b displaystyle b sutun matrisinin konulmus oldugu matrisdir Iki degiskenli iki dogrusal denklemli dizge ornegi Bu ornekte determinantlarin icinde hangi elemanlar bulundugunun hemen anlasilmasi iccin katsayilar ai j displaystyle color blue a i j mavi renkli bilinmeyenler xi displaystyle color blue x i siyah renkli ve katsayilar bi displaystyle color OliveGreen b i yesil renkli yazilmistir 4x1 2x2 242x1 3x2 16 displaystyle begin matrix color blue 4 color black x 1 color blue 2 color black x 2 color OliveGreen 24 color blue 2 color black x 1 color blue 3 color black x 2 color OliveGreen 16 end matrix x1 det A1 det A 242163 4223 24 3 16 28 408 5 displaystyle x 1 frac det A 1 det A frac begin vmatrix color OliveGreen 24 amp color blue 2 color OliveGreen 16 amp color blue 3 end vmatrix begin vmatrix color blue 4 amp color blue 2 color blue 2 amp color blue 3 end vmatrix 24 cdot 3 16 cdot 2 over 8 40 over 8 5 x2 det A2 det A 424216 4223 4 16 2 248 168 2 displaystyle x 2 frac det A 2 det A frac begin vmatrix color blue 4 amp color OliveGreen 24 color blue 2 amp color OliveGreen 16 end vmatrix begin vmatrix color blue 4 amp color blue 2 color blue 2 amp color blue 3 end vmatrix 4 cdot 16 2 cdot 24 over 8 16 over 8 2 Uc degiskenli uc dogrusal denklemli dizge ornegi 82x1 45x2 9x3 127x1 16x2 3x3 19x1 5x2 1x3 0 displaystyle begin matrix color blue 82 color black x 1 color blue 45 color black x 2 color blue 9 color black x 3 color OliveGreen 1 color blue 27 color black x 1 color blue 16 color black x 2 color blue 3 color black x 3 color OliveGreen 1 color blue 9 color black x 1 color blue 5 color black x 2 color blue 1 color black x 3 color OliveGreen 0 end matrix x1 det A1 det A 14591163051 8245927163951 11 1 displaystyle x 1 frac det A 1 det A frac begin vmatrix color OliveGreen 1 amp color blue 45 amp color blue 9 color OliveGreen 1 amp color blue 16 amp color blue 3 color OliveGreen 0 amp color blue 5 amp color blue 1 end vmatrix begin vmatrix color blue 82 amp color blue 45 amp color blue 9 color blue 27 amp color blue 16 amp color blue 3 color blue 9 amp color blue 5 amp color blue 1 end vmatrix frac 1 1 1 qquad x2 det A2 det A 82192713901 8245927163951 11 1 displaystyle x 2 frac det A 2 det A frac begin vmatrix color blue 82 amp color OliveGreen 1 amp color blue 9 color blue 27 amp color OliveGreen 1 amp color blue 3 color blue 9 amp color OliveGreen 0 amp color blue 1 end vmatrix begin vmatrix color blue 82 amp color blue 45 amp color blue 9 color blue 27 amp color blue 16 amp color blue 3 color blue 9 amp color blue 5 amp color blue 1 end vmatrix frac 1 1 1 qquad x3 det A3 det A 8245127161950 8245927163951 141 14 displaystyle x 3 frac det A 3 det A frac begin vmatrix color blue 82 amp color blue 45 amp color OliveGreen 1 color blue 27 amp color blue 16 amp color OliveGreen 1 color blue 9 amp color blue 5 amp color OliveGreen 0 end vmatrix begin vmatrix color blue 82 amp color blue 45 amp color blue 9 color blue 27 amp color blue 16 amp color blue 3 color blue 9 amp color blue 5 amp color blue 1 end vmatrix frac 14 1 14 Diger yontemlerHomojen dizgelerTanimlama Bir dogrusal denklemler dizgesinde sabitlerin hepsi 0 iselr bu dogrsusal denklemler dizgesi homojen dizge olarak tanimlanir a11x1 a12x2 a1nxn 0a21x1 a22x2 a2nxn 0 am1x1 am2x2 amnxn 0 displaystyle begin alignedat 7 a 11 x 1 amp amp amp amp a 12 x 2 amp amp cdots amp amp a 1n x n amp amp amp amp amp 0 a 21 x 1 amp amp amp amp a 22 x 2 amp amp cdots amp amp a 2n x n amp amp amp amp amp 0 vdots amp amp amp amp vdots amp amp amp amp vdots amp amp amp amp amp vdots a m1 x 1 amp amp amp amp a m2 x 2 amp amp cdots amp amp a mn x n amp amp amp amp amp 0 end alignedat Matris ifadesiyle bir genel homojen dizge soyle ifade edilir Ax 0 displaystyle A textbf x textbf 0 Burada A mxn duzenli katsayilar matrisi x n sirali degiskenler vektoru veya sutun matrisi ve 0 m sirali veya 0 girdili sutun matris olur Cozum kumesi Her homojen dizgenin en asagi bir tane cozumu vardir bu her degiskenin 0 a esit oldugu cozum kumesidir Bu cozume sifir cozumu veya onemsiz trivial cozum adi verilir Homoojen dizgelerin onemli olan su diger nitelikleri de bulunur Eger u ve v homojen dizgenin iki cozum vektoru iseler u v displaystyle u v vektorler toplami da homojen dizgenin bir cozumu olur Eger u bir homojen dizgenin bir cozumunu ifade etmekte ise ve z herhangi bir skaler deger ise o zaman ru displaystyle ru vektor carpimi da homojen dizgenin bir cozumudur Bu cozum kumesi nitelikleri R lt sup gt n lt sup gt nin bir Euclid tipi altuzayi icin gerekli nitelikler ile tipatip aynidir Ozellikle bir homojen dizgenin cozum kumesi buna tekabul eden A matrisinin ile aynidir Homojen olmayan dizgelerle iliskilerKaynakcaIngilizce Wikipedia System of linear equations maddesi 5 Mart 2011 tarihinde Wayback Machine sitesinde arsivlendi Ingilizce Ayrica bakinizDis baglantilarITU Ninova Acik Ders Malzemeleri olu kirik baglanti Dogrusal cebir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans