Fizikte (özellikle gazların kinetik teorisinde) Einstein ilişkisi; 1904'te 'in, 1905'te Albert Einstein'ın ve 1906'da Marian Smoluchowski'ninBrown hareketi üzerine yaptıkları çalışmalarında bağımsız olarak ortaya koydukları önceden beklenmedik bir bağlantıdır. Denklemin daha genel biçimi:
burada;
- D ;
- μ, "hareketlilik" veya parçacığın terminal sürüklenme hızının uygulanan bir kuvvete oranıdır, μ = vd/F;
- kB, Boltzmann sabitidir;
- T mutlak sıcaklıktır.
Bu denklem, bir erken bir örneğidir.
İlişkinin sık kullanılan iki önemli özel biçimi şunlardır:
- (elektriksel hareketlilik denklemi, yüklü parçacıkların difüzyonu için
- (Stokes-Einstein denklemi, küresel parçacıkların düşük Reynolds sayılı bir sıvıdan difüzyonu için)
burada;
- q, bir parçacığın elektrik yüküdür;
- μq, yüklü parçacığın
- η dinamik viskozitedir;
- r, küresel parçacığın yarıçapıdır.
Özel durumlar
Elektriksel hareketlilik denklemi
Elektrik yükü q olan bir parçacık için, elektriksel hareketliliği μq, genelleştirilmiş hareketliliği μ ile μ = μq/q denklemiyle ilişkilidir. μq parametresi, parçacığın terminal sürüklenme hızının uygulanan bir elektrik alanına oranıdır. Bu nedenle, yüklü bir parçacık durumunda denklem şu şekilde verilir:
burada;
difüzyon katsayısıdır (
).
(
).
parçacığın elektrik yüküdür (C, coulomb)
plazmadaki elektron sıcaklığı veya iyon sıcaklığıdır (K).
Sıcaklık, plazma için daha yaygın olan Volt cinsinden verilirse:
burada;
parçacığın (birimsiz)
plazmadaki elektron sıcaklığı veya iyon sıcaklığıdır (V).
Stokes-Einstein denklemi
Düşük Reynolds sayısı sınırında; hareketlilik μ, sürtünme katsayısı 

burada 
Bu, sıvılarda öz-difüzyon katsayısını tahmin etmek için uzun yıllar boyunca uygulandı ve izomorf teorisi ile tutarlı bir versiyon, Lennard-Jones sisteminin bilgisayar simülasyonları ile doğrulandı.
durumunda, sürtünme 

Yarı iletken
Rastgele bir sahip bir yarı iletkende, yani deliklerin veya elektronların yoğunluğu 


burada 
burada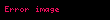
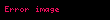
Nernst-Einstein denklemi
Bir elektrolitin ifadelerinden katyonların ve anyonların elektrik iyonik hareketlilik ifadelerindeki difüziviteleri değiştirerek, Nernst-Einstein denklemi türetilir:
Genel durumun kanıtı
Einstein ilişkisinin kanıtı birçok referansta bulunabilir, örneğin bkz. Kubo.
Bazı sabit, harici potansiyel enerji 






Sürüklenme akımı nedeniyle parçacıkların net akışı:
yani, belirli bir konumdan geçen parçacıkların sayısı, parçacık konsantrasyonu çarpı ortalama hıza eşittir.
Difüzyon akımı nedeniyle parçacıkların akışı, göre,
burada eksi işareti, parçacıkların daha yüksek derişimden daha düşük derişime aktığı anlamına gelir.
Şimdi denge durumunu düşünün. İlk olarak, net akış yoktur, yani 




Bu nedenle, dengede:
Bu ifade her 
Klasik parçacıklar için 

burada 
Bu varsayım altında, bu denklemi genel Einstein ilişkisine dahil etmek şunları verir:
ki bu klasik Einstein ilişkisine karşılık gelir.
Ayrıca bakınız
Kaynakça
- ^ World Year of Physics – William Sutherland at the University of Melbourne 29 Haziran 2021 tarihinde Wayback Machine sitesinde .. Essay by Prof. R Home (with contributions from Prof B. McKellar and A./Prof D. Jamieson) dated 2005. Accessed 2017-04-28.
- ^ Sutherland William (1905). "LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin". Philosophical Magazine. Series 6. 9 (54): 781-785. doi:10.1080/14786440509463331. 24 Haziran 2021 tarihinde kaynağından . Erişim tarihi: 24 Haziran 2021.
- ^ P. Hänggi, "Stokes–Einstein–Sutherland equation" 24 Haziran 2021 tarihinde Wayback Machine sitesinde ..
- ^ Einstein, A. (1905). "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen". Annalen der Physik (Almanca). 322 (8): 549-560. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806. 10 Mayıs 2021 tarihinde kaynağından . Erişim tarihi: 23 Haziran 2021.
- ^ von Smoluchowski, M. (1906). "Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen". Annalen der Physik (Almanca). 326 (14): 756-780. Bibcode:1906AnP...326..756V. doi:10.1002/andp.19063261405. 24 Haziran 2021 tarihinde kaynağından . Erişim tarihi: 23 Haziran 2021.
- ^ Dill, Ken A.; Bromberg, Sarina (2003). Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology (İngilizce). Garland Science. s. 327. ISBN . 24 Haziran 2021 tarihinde kaynağından . Erişim tarihi: 23 Haziran 2021.
- ^ Umberto Marini Bettolo Marconi, Andrea Puglisi, Lamberto Rondoni, Angelo Vulpiani, "Fluctuation-Dissipation: Response Theory in Statistical Physics".
- ^ Van Zeghbroeck, "Principles of Semiconductor Devices", Chapter 2.7 6 Mayıs 2021 tarihinde Wayback Machine sitesinde ..
- ^ Gas Discharge Physics. Springer. 2001. ss. 20-28. ISBN .
- ^ Costigliola, Lorenzo; Heyes, David M.; Schrøder, Thomas B.; Dyre, Jeppe C. (14 Ocak 2019). "Revisiting the Stokes-Einstein relation without a hydrodynamic diameter". The Journal of Chemical Physics (İngilizce). 150 (2). s. 021101. ISSN 0021-9606. (PMID) 30646717. 24 Haziran 2021 tarihinde kaynağından . Erişim tarihi: 24 Haziran 2021.
- ^ Ashcroft, N. W.; Mermin, N. D. (1988). Solid State Physics. New York (USA): Holt, Rineheart and Winston. s. 826.
- ^ Bonnaud, Olivier (2006). Composants à semiconducteurs (Fransızca). Paris (France): Ellipses. s. 78.
- ^ Kubo, R. (1966). "The fluctuation-dissipation theorem". 29 (1): 255-284. Bibcode:1966RPPh...29..255K. doi:10.1088/0034-4885/29/1/306.
Dış bağlantılar
- Einstein ilişki hesaplayıcıları
- İyon yayılımı 24 Haziran 2021 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte ozellikle gazlarin kinetik teorisinde Einstein iliskisi 1904 te in 1905 te Albert Einstein in ve 1906 da Marian Smoluchowski ninBrown hareketi uzerine yaptiklari calismalarinda bagimsiz olarak ortaya koyduklari onceden beklenmedik bir baglantidir Denklemin daha genel bicimi D mkBT displaystyle D mu k text B T burada D m hareketlilik veya parcacigin terminal suruklenme hizinin uygulanan bir kuvvete oranidir m vd F kB Boltzmann sabitidir T mutlak sicakliktir Bu denklem bir erken bir ornegidir Iliskinin sik kullanilan iki onemli ozel bicimi sunlardir D mqkBTq displaystyle D frac mu q k text B T q elektriksel hareketlilik denklemi yuklu parcaciklarin difuzyonu icin D kBT6phr displaystyle D frac k text B T 6 pi eta r Stokes Einstein denklemi kuresel parcaciklarin dusuk Reynolds sayili bir sividan difuzyonu icin burada q bir parcacigin elektrik yukudur mq yuklu parcacigin h dinamik viskozitedir r kuresel parcacigin yaricapidir Ozel durumlarElektriksel hareketlilik denklemi Elektrik yuku q olan bir parcacik icin elektriksel hareketliligi mq genellestirilmis hareketliligi m ile m mq q denklemiyle iliskilidir mq parametresi parcacigin terminal suruklenme hizinin uygulanan bir elektrik alanina oranidir Bu nedenle yuklu bir parcacik durumunda denklem su sekilde verilir D mqkBTq displaystyle D frac mu q k text B T q burada D displaystyle D difuzyon katsayisidir m2s 1 displaystyle mathrm m 2 s 1 mq displaystyle mu q m2V 1s 1 displaystyle mathrm m 2 V 1 s 1 q displaystyle q parcacigin elektrik yukudur C coulomb T displaystyle T plazmadaki elektron sicakligi veya iyon sicakligidir K Sicaklik plazma icin daha yaygin olan Volt cinsinden verilirse D mqTZ displaystyle D frac mu q T Z burada Z displaystyle Z parcacigin birimsiz T displaystyle T plazmadaki elektron sicakligi veya iyon sicakligidir V Stokes Einstein denklemi Dusuk Reynolds sayisi sinirinda hareketlilik m surtunme katsayisi z displaystyle zeta nin tersidir Yayilan nesnenin ters momentum gevseme suresi atalet momentumunun rastgele momente kiyasla ihmal edilebilir hale gelmesi icin gereken sure icin bir sonum sabiti g z m displaystyle gamma zeta m siklikla kullanilir Yaricapi r olan kuresel parcaciklar icin z 6phr displaystyle zeta 6 pi eta r burada h displaystyle eta ortamin viskozitesidir Boylece Einstein Smoluchowski iliskisi Stokes Einstein iliskisi ile sonuclanir D kBT6phr displaystyle D frac k text B T 6 pi eta r Bu sivilarda oz difuzyon katsayisini tahmin etmek icin uzun yillar boyunca uygulandi ve izomorf teorisi ile tutarli bir versiyon Lennard Jones sisteminin bilgisayar simulasyonlari ile dogrulandi durumunda surtunme zr 8phr3 displaystyle zeta text r 8 pi eta r 3 ve rotasyonel difuzyon sabiti Dr displaystyle D text r Dr kBT8phr3 displaystyle D text r frac k text B T 8 pi eta r 3 Yari iletken Rastgele bir sahip bir yari iletkende yani deliklerin veya elektronlarin yogunlugu p displaystyle p ve karsilik gelen veya elektrokimyasal potansiyel f displaystyle varphi arasindaki p p f displaystyle p p varphi formunun bir iliskisi Einstein iliskisi soyledir D mqpqdpdf displaystyle D frac mu q p q frac dp d varphi burada mq displaystyle mu q Durumlarin yogunlugu icin parabolik bir dagilim iliskisini varsayan bir ornek ve genellikle inorganik yari iletken malzemeleri tanimlamak icin kullanilan hesaplanabilir p f N0eqfkBT displaystyle p varphi N 0 e frac q varphi k text B T buradaN0 displaystyle N 0 N0 displaystyle N 0 basitlestirilmis iliskiyi veren mevcut enerji durumlarinin toplam yogunlugudur D mqkBTq displaystyle D mu q frac k text B T q Nernst Einstein denklemi Bir elektrolitin ifadelerinden katyonlarin ve anyonlarin elektrik iyonik hareketlilik ifadelerindeki difuziviteleri degistirerek Nernst Einstein denklemi turetilir Le zi2F2RT D D displaystyle Lambda e frac z i 2 F 2 RT D D Genel durumun kanitiEinstein iliskisinin kaniti bircok referansta bulunabilir ornegin bkz Kubo Bazi sabit harici potansiyel enerji U displaystyle U nun belirli bir x displaystyle mathbf x konumunda bulunan bir parcacik uzerinde korunumlu bir F x U x displaystyle F mathbf x nabla U mathbf x kuvveti ornegin bir elektrik kuvveti olusturdugunu varsayalim Parcacigin v x m x F x displaystyle v mathbf x mu mathbf x F mathbf x hiziyla hareket ederek tepki verecegini varsayiyoruz Simdi konumun bir fonksiyonu olarak yerel derisim r x displaystyle rho mathbf x olan cok sayida boyle parcacik oldugunu varsayalim Bir sure sonra denge kurulacaktir parcaciklar en dusuk potansiyel enerji U displaystyle U ya sahip alanlarin etrafinda yigilacaktir ancak yine de difuzyon nedeniyle bir dereceye kadar yayilacaktir Dengede parcaciklarin net akisi yoktur parcaciklarin suruklenme akimi olarak adlandirilan daha dusuk U displaystyle U ya dogru cekilme egilimi parcaciklarin difuzyon nedeniyle yayilma egilimini mukemmel bir sekilde dengeler ve buna difuzyon akimi denir bkz Suruklenme akimi nedeniyle parcaciklarin net akisi Jdrift x m x F x r x r x m x U x displaystyle mathbf J mathrm drift mathbf x mu mathbf x F mathbf x rho mathbf x rho mathbf x mu mathbf x nabla U mathbf x yani belirli bir konumdan gecen parcaciklarin sayisi parcacik konsantrasyonu carpi ortalama hiza esittir Difuzyon akimi nedeniyle parcaciklarin akisi gore Jdiffusion x D x r x displaystyle mathbf J mathrm diffusion mathbf x D mathbf x nabla rho mathbf x burada eksi isareti parcaciklarin daha yuksek derisimden daha dusuk derisime aktigi anlamina gelir Simdi denge durumunu dusunun Ilk olarak net akis yoktur yani Jdrift Jdiffusion 0 displaystyle mathbf J mathrm drift mathbf J mathrm diffusion 0 Ikincisi etkilesmeyen nokta parcaciklar icin denge yogunlugu r displaystyle rho yalnizca yerel potansiyel enerji U displaystyle U nin bir fonksiyonudur yani iki konum ayni U displaystyle U ya sahipse o zaman ayni r displaystyle rho ye de sahip olacaklardir ornegin asagida tartisildigi gibi bakiniz Bunun anlami zincir kuralinin uygulanmasi r drdU U displaystyle nabla rho frac mathrm d rho mathrm d U nabla U Bu nedenle dengede 0 Jdrift Jdiffusion mr U D r mr DdrdU U displaystyle 0 mathbf J mathrm drift mathbf J mathrm diffusion mu rho nabla U D nabla rho left mu rho D frac mathrm d rho mathrm d U right nabla U Bu ifade her x displaystyle mathbf x konumunda gecerli oldugundan Einstein iliskisinin genel bicimini ifade eder D mrdrdU displaystyle D mu frac rho frac mathrm d rho mathrm d U Klasik parcaciklar icin r displaystyle rho ve U displaystyle U arasindaki iliski modellenebilir r x Ae U x kBT displaystyle rho mathbf x Ae frac U mathbf x k rm B T burada A displaystyle A toplam parcacik sayisiyla ilgili bir sabittir Bu nedenle drdU 1kBTr displaystyle frac mathrm d rho mathrm d U frac 1 k rm B T rho Bu varsayim altinda bu denklemi genel Einstein iliskisine dahil etmek sunlari verir D mrdrdU mkBT displaystyle D mu frac rho frac mathrm d rho mathrm d U mu k rm B T ki bu klasik Einstein iliskisine karsilik gelir Ayrica bakinizKaynakca World Year of Physics William Sutherland at the University of Melbourne 29 Haziran 2021 tarihinde Wayback Machine sitesinde Essay by Prof R Home with contributions from Prof B McKellar and A Prof D Jamieson dated 2005 Accessed 2017 04 28 Sutherland William 1905 LXXV A dynamical theory of diffusion for non electrolytes and the molecular mass of albumin Philosophical Magazine Series 6 9 54 781 785 doi 10 1080 14786440509463331 24 Haziran 2021 tarihinde kaynagindan Erisim tarihi 24 Haziran 2021 P Hanggi Stokes Einstein Sutherland equation 24 Haziran 2021 tarihinde Wayback Machine sitesinde Einstein A 1905 Uber die von der molekularkinetischen Theorie der Warme geforderte Bewegung von in ruhenden Flussigkeiten suspendierten Teilchen Annalen der Physik Almanca 322 8 549 560 Bibcode 1905AnP 322 549E doi 10 1002 andp 19053220806 10 Mayis 2021 tarihinde kaynagindan Erisim tarihi 23 Haziran 2021 von Smoluchowski M 1906 Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen Annalen der Physik Almanca 326 14 756 780 Bibcode 1906AnP 326 756V doi 10 1002 andp 19063261405 24 Haziran 2021 tarihinde kaynagindan Erisim tarihi 23 Haziran 2021 Dill Ken A Bromberg Sarina 2003 Molecular Driving Forces Statistical Thermodynamics in Chemistry and Biology Ingilizce Garland Science s 327 ISBN 9780815320517 24 Haziran 2021 tarihinde kaynagindan Erisim tarihi 23 Haziran 2021 Umberto Marini Bettolo Marconi Andrea Puglisi Lamberto Rondoni Angelo Vulpiani Fluctuation Dissipation Response Theory in Statistical Physics Van Zeghbroeck Principles of Semiconductor Devices Chapter 2 7 6 Mayis 2021 tarihinde Wayback Machine sitesinde Gas Discharge Physics Springer 2001 ss 20 28 ISBN 978 3540194620 Costigliola Lorenzo Heyes David M Schroder Thomas B Dyre Jeppe C 14 Ocak 2019 Revisiting the Stokes Einstein relation without a hydrodynamic diameter The Journal of Chemical Physics Ingilizce 150 2 s 021101 ISSN 0021 9606 PMID 30646717 24 Haziran 2021 tarihinde kaynagindan Erisim tarihi 24 Haziran 2021 Ashcroft N W Mermin N D 1988 Solid State Physics New York USA Holt Rineheart and Winston s 826 Bonnaud Olivier 2006 Composants a semiconducteurs Fransizca Paris France Ellipses s 78 Kubo R 1966 The fluctuation dissipation theorem 29 1 255 284 Bibcode 1966RPPh 29 255K doi 10 1088 0034 4885 29 1 306 Dis baglantilarEinstein iliski hesaplayicilari Iyon yayilimi 24 Haziran 2021 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans

























