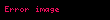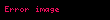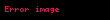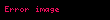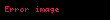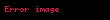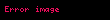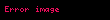Rotasyonel

${\displaystyle {\vec {F}}(x,y,z)}$ ile gösterilen bir vektör alanının rotasyoneli, nabla operatörü (${\displaystyle {\vec {\nabla }}}$) ile ${\displaystyle {\vec {F}}}$'nin vektörel çarpımına eşittir.

${\displaystyle \operatorname {rot} {\vec {F}}={\vec {\nabla }}\times {\vec {F}}=\operatorname {det} {\begin{vmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\F_{x}&F_{y}&F_{z}\end{vmatrix}}=\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right){\hat {i}}-\left({\frac {\partial F_{z}}{\partial x}}-{\frac {\partial F_{x}}{\partial z}}\right){\hat {j}}+\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right){\hat {k}}}$

Tensör gösterimi (${\displaystyle \epsilon _{ijk}\,}$, olmak üzere):

${\displaystyle \nabla \times F=\epsilon _{ijk}\partial _{j}F_{k}e_{i}=e_{i}\epsilon _{ijk}F_{k,j}}$

${\displaystyle \phi \,}$ skaler bir alan, ${\displaystyle {\vec {F}}}$ ve ${\displaystyle {\vec {G}}}$ de vektörel birer alan olmak üzere, rotasyonel alma işleminin özellikleri şöyle sıralanabilir:

${\displaystyle {\vec {\nabla }}\times ({\vec {F}}+{\vec {G}})={\vec {\nabla }}\times {\vec {F}}+{\vec {\nabla }}\times {\vec {G}}}$
${\displaystyle {\vec {\nabla }}\times (\phi {\vec {F}})=({\vec {\nabla }}\phi )\times {\vec {F}}+\phi ({\vec {\nabla }}\times {\vec {F}})}$
${\displaystyle \nabla \times (\nabla \phi )=0}$
${\displaystyle \nabla \cdot (\nabla \times {\vec {F}})=0}$
$${\displaystyle \nabla \times (\nabla \times \phi )=-\nabla ^{2}\phi +\nabla \cdot (\nabla \cdot \phi )}$$