Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Einstein senkronizasyonu (veya Poincaré–Einstein senkronizasyonu), farklı yerlerdeki saatlerin sinyal değişimleri vasıtasıyla senkronize edilmesi yöntemidir. Bu senkronizasyon yöntemi, halihazırda 19. yüzyılın ortalarında telegrafçılar tarafından kullanılmıştır; ancak ışık sinyalleri üzerine uygulayan ve görelelik teorisindeki temel rolünü fark eden Henri Poincaré ve Albert Einstein tarafından meşhur edilmiştir. Temel değeri, tek bir eylemsiz çerçevedeki saatler içindir.
Einstein
Einstein'ın 1905'teki formülüne göre,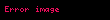 
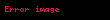
anında 1 no.lu saat'ten 2 no.lu saat'e doğru bir ışık sinyali gönderiliyor ve aynı anda geri dönüyor, mesela bir ayna vasıtasıyla, ışık sinyalinin 1 no.lu saat'e geri ulaştığındaki süre ise 
olsun. Bu senkronizasyon yöntemi 2 no.lu saat'in 1 no.lu saatle eşzamanlı yapılması (senkronizasyonu) için yapılır ve bu senkronizasyonda ışın yansımasının olduğu ana ise 
diyebiliriz.
![image]()
.
olarak tanımlanır.
Aynı senkronizasyon, taşıma hızının kaybolacağı kadar "yavaş" bir limitte, üçüncü bir saat'i, 1 no.lu saat'ten 2 no.lu saat'e taşıyarak da elde edilir. Literatürde tartışılmasına rağmen saat senkronizasyonu için pek çok fikir deneyi de aynı sonucu vermiştir.
Sorun, bu senkronizasyonun gerçekten tutarlı bir şekilde herhangi bir olaya bir zaman etiketi atamada barışılı olup olmadığıdır. Bu amaçla koşulları sağlayan bir durum bulunmalıdır.
(a) saatler bir kez senkronize edilince senkronize kalırlar,
(b1) senkronizasyon , yani her saat kendi tarafından senkronize edilir (otomatik olarak şartları yerine getirdi),
(b2) senkronizasyon , yani eğer saat A saat B ile senkronize ise, saat B de saat A ile senkronizedir,
(b3) senkronizasyon , yani eğer saat A saat B ile senkronize ve saat B de saat C ile senkronizeyse, saat A saat C ile senkronizedir.
Eğer (a) noktası tutuyorsa o zaman saatlerin senkronize olduğunu söylemek mantıklıdır. Verilen (a)da, eğer (b1)–(b3) tutuyorsa o zaman senkronizasyon küresel zaman fonksiyonu t'yi kurmamıza olanak tanır. t=sabit dilimler "eşzamanlılık dilimi" olarak adlandırılır.
Einstein (1905) (a) ve (b1)–(b3)ün ışığın ilerleyişinin fiziksel özellikleriyle kolaylıkla doğrulanabileceğine indirgenme ihtimalini fark etmedi. Onun yerine "Bu senkronizasyon tanımının çelişkilerden bağımsız olduğunu varsayalım ve her sayıdaki nokta için mümkün olduğunu; ve takip eden (b2–b3) ilişkiler evrensel olarak geçerlidir.."Bu nedenle ve yeni gelişmelerin pek de iyi bilinmemesinden dolayı, bazı fiziksel makaleler hala görelik kuramı önermeleri arasında Einstein senkronizasyonunun tutarlılığı varsayımını sunmaktadır.[]
Max Von Laue ilk kez Einstein'ın senkronizasyonunun tutarlılığı problemini çalışan kişidir). L. Silberstein, çoğu iddialarını görelik üzerine olan kitabında okuyucular için alıştırma olarak bırakmasına rağmen, benzer bir çalışma sunmuştur. Max von Laue'nin tezleri H. Reichenbach and found a final shape in a work by A. Macdonald. tarafından yeniden ele alındı ve A. MacDonald tarafından çalışmalarında son şekline kavuştu. Einstein senkronizasyonunun önceki koşulları sağlıyor oluşunun çözümü ancak ve ancak takip eden iki koşulla karşılanır.
(i) Kırmızıya kayma olmayacak: Eğer A noktasından A'daki saat tarafından kaydedilen ve Dt kadar zaman sonra iki parlama gönderilirse, B'deki bir saat tarafından kaydedilmiş Dt kadar zaman sonra ayrı ayrı B'ye ulaşırlar.
(ii) Reichenbach'ın gidiş-dönüş koşulu: Eğer bir ışık demeti A'dan başlayan ABC üçgeni üzerine gönderilirse (ve B ve C'deki aynalarca yansıtılan), bu durumda A noktasına geri dönme olayı takip edilen istikametten bağımsızdır (ABCA veya ACBA). Bir kez saatler senkronize edilince tek yönlü ışık hızını ölçebilir. Buna rağmen, Einstein'ın senkronizasyonunun uygulanabilirliğini garanti eden önceki koşullar, tek yönlü ışık hızının her karede aynı olarak ortaya çıkacağı anlamına gelmez. Düşünün
(iii)Von Laue ve Weyl's'nin gidiş-dönüş koşulu: L uzunluğundaki bir kapalı yoldan ışık ışınının geçmesi için gereken zaman L/cdir. Burada L yolun uzunluğu ve c de yoldan bağımsız bir sabittir.
Bir teori (çıkış noktası von Laue ve Weyl'ye kadar takip edilebilir) ancak ve ancak Einstein senkronizasyonunun sürekli uygulanabilir olduğunda Laue-Weyl'nin gidiş dönüş koşulunu sağlar (örneğin (a) ve (b1)–(b3) sağlar) ve senkronize saatlere göreli tek yönlü ışık hızı tüm karelerde sabittir. Laue-Weyl koşulunun önemi, bahsi geçen zamanın sadece bir saatle ölçülebileceği gerçeğinin üstüne kuruludur buna göre bu koşul senkronizasyon kurallarına dayanmaz ve deneysel olarak kontrol edilebilir. Nitekim, Laue-Weyl gidiş-dönüş koşulunun sağladığı eylemsizlik çerçevesinde deneysel olarak doğrulanmıştır.
Uzak saatlerin senkronizasyonundan önce tek yönlü hızı ölçmek anlamsız olduğundan, tek yönlü ışık hızı ölçümü iddiasındaki deneylerin genelde Laue-Weyl gidiş dönüş koşullarının yeniden yorumlanmasının doğrulanması olarak görülmesi mümkündür.
Einstein senkronizasyonu sadece böyle doğal görünür. Kolaylıkla bunun yalnızca bir anlaşma olduğu unutulabilir. Dönen çerçevelerde, özel görelilikte bile, Einstein senkronizasyonu dışı geçişlilik yararlılığını azaltır. Eğer saat 1 ve saat 2 doğrudan senkronize değilse, saatler arası bir zincir kullanılmışsa, senkronizasyon seçilen yola bağlıdır. Dönen diskin çevresindeki senkronizasyon, kullanılan yola bağlı azalmayan zaman farkını verir. Bu ve Ehrenfest paradoksunda önemlidir. Küresel konumlandırma sistemi GPS bu konudan etkilenir.
Einstein senkronizasyonunun uzlaşımcılığının somut tartışmaları Reichenbach'a dayanır. Bu senkronizasyonun alışılmışlığını inkâr girişimlerinin yalanlandığı kabul edilir, argümanlarının kayda değer bir hariç tutulması ile, nedensel bağlantının küresel ilişkisinden çıkarılabilir. Bu yerleşse de yerleşmese de konu tartışmalıdır.
Tarihçe: Poincaré
Senkronizasyonun alışılmışlığının bazı özellikleri Henri Poincaré tarafından öngörülmüştür.1898 yılında (felsefi bir makalede) ışık hızının tüm yönlerde sabit olması ilkesinin fiziksel kanunlar ile basit bir şekilde formülize edilmesinin faydasını savundu. Ayrıca farklı yerlerdeki olayların eşzamanlılığının tanımının sadece bir kuralı olduğunu gösterdi. Bu kurallara dayanarak, ama şimdilerde yürürlükten kaldırılmış çerçevesinde, 1900 yılında Poincaré saat senkronizasyonunu tanımlamak için aşağıdaki kuralı önerdi: esîr içinde hareket eden iki gözlemci A ve B, saatlerini optik sinyaller aracılığıyla senkronize eder. Görelilik ilkesinden ötürü esîrde durağan olacağına inanırlar ve ışık hızının tüm yönlerde sabit olacağını kabul ederler. Bu nedenle sinyallerin sadece iletim süresini göz önünde bulundurmanız gerekir ve daha sonra gözlemcilerin geçişlerini incelemesi gerekir, saatleri senkronize olsun veya olmasın.
Çeşitli noktalara yerleştirilecek bazı gözlemciler olduğunu varsayalım ve ışık sinyallerini kullanarak kendi saatlerini senkronize etsinler. Ölçülen sinyallerin iletim sürelerini ayarlama girişiminde bulunurlar, ancak ortak hareketlerinin farkında değillerdir ve sonuç olarak sinyallerin eşit hızla iki yönde de yolculuk edeceğini düşünelim. Geçiş sinyallerinin gözlemlerini gerçekleştirirler, biri A'dan B'ye yol alır, B'den A'ya farklı bir yolculukla takip edilir. Ayarlanmış saatler tarafından gösterilen
yerel zamandır. Eğer
ışık hızı ise,
de dünyanın hızıdır ki biz onu
eksenine paralel kabul ediyoruz ve pozitif yönde olduğunu. Böylece;
.
1904 yılında Poincaré aynı prosedürü aşağıdaki yöntemle göstermiştir:
Optik sinyallere göre kendi saatler ayarlamak isteyen iki gözlemci düşünün; sinyalleri değişsinler, ancak onların da bildiği gibi ışık iletimi anlık değildir, onlar geçmek için dikkatlidir. İstasyon B, istasyon A'nın sinyalini algıladığı zaman, istasyon A'nın saati sinyal gönderme anında saat işaretlememelidir ama bu saat iletim süresini temsil eden bir sabite göre artar. Varsayalım ki, örneğin, istasyon A saati saat 0'ı işaretlediğinde sinyalini göndersin ve istasyon B o sinyali algılasın ve 
saatini işaretlesin. Eğer t=yavaşlık iletim süresini temsil ediyorsa saatler ayarlanır ve bunu doğrulamak için istasyon B kendi sırasında bir sinyal gönderir ve saatini 0'a işaretler; sonra istasyon A algıladığında saatini t olarak işaretlemelidir. Sonra kronometreler ayarlanır. Ve aslında onlar aynı fiziksel anda aynı saati işaretler, ama bir şartla, iki istasyon sabit olduğunda. Aksi halde iletim süresi iki anlamda aynı olmaz, çünkü istasyon A, örneğin, B'den kaynaklanan optik karışıklığı karşılamak için ileri gider ancak istasyon B ise A'dan kaynaklanan karışıklık gelmeden önce kaçar. Bu şekilde ayarlanmış saatler işaretlenmez, bu nedenle, gerçek zaman; işaretleme yaparlar ve bu işarete yerel zaman denir, bu yüzden bunlardan biri diğerinden yavaş olur.
Kaynakça
- ^ Einstein, A. (1905), (PDF), Annalen der Physik, 17 (10), ss. 891-921, Bibcode:1905AnP...322..891E, doi:10.1002/andp.19053221004, 20 Şubat 2005 tarihinde kaynağından (PDF) arşivlendi, erişim tarihi: 10 Ocak 2015. See also English translation 25 Kasım 2005 tarihinde Wayback Machine sitesinde .
- ^ Laue, M. (1911), Das Relativitätsprinzip, Braunschweig: Friedr. Vieweg & Sohn.
- ^ Minguzzi, E., "The Poincaré-Einstein synchronization: historical aspects and new developments", . Phys.: Conf. Ser., cilt 306, s. 012059, Bibcode:2011JPhCS.306a2059M, doi:10.1088/1742-6596/306/1/012059
- ^ Silberstein, L. (1914), The theory of relativity, Londra: Macmillan.
- ^ Reichenbach, H. (1969), Axiomatization of the Theory of Relativity, Berkeley: University of California Press.
- ^ Macdonald, A. (1983), "Clock synchronization, a universal light speed, and the terrestrial red-shift experiment", American Journal of Physics, 51 (9), ss. 795-797, Bibcode:1983AmJPh..51..795M, doi:10.1119/1.13500
- ^ Minguzzi, E. and Macdonald, A. (2003), "Universal one-way light speed from a universal light speed over closed paths", Foundations of Physics Letters, 16 (6), ss. 593-604, arXiv:gr-qc/0211091 $2, Bibcode:2003FoPhL..16..593M, doi:10.1023/B:FOPL.0000012785.16203.52
- ^ Weyl, H. (1988), Raum Zeit Materie, New York: Springer-Verlag Seventh edition based on the fifth German edition (1923).
- ^ Galison (2002).
- ^ Darrigol (2005).
- ^ Poincaré, Henri (1898), "The Measure of Time", The foundations of science, New York: Science Press, ss. 222-234
- ^ Poincaré, Henri (1900), "La théorie de Lorentz et le principe de réaction", Archives néerlandaises des sciences exactes et naturelles, cilt 5, ss. 252-278. See also the English translation 26 Haziran 2008 tarihinde Wayback Machine sitesinde ..
- ^ Poincaré, Henri (1904), "The Principles of Mathematical Physics", Congress of arts and science, universal exposition, St. Louis, 1904, 1, Boston and New York: Houghton, Mifflin and Company, ss. 604-622
Yazılar
- Darrigol, Olivier (2005), "The Genesis of the theory of relativity" (PDF), Séminaire Poincaré, cilt 1, ss. 1-22, doi:10.1007/3-7643-7436-5_1, 8 Kasım 2018 tarihinde kaynağından (PDF), erişim tarihi: 12 Ocak 2015
- , Becoming, relativity and locality, in The Ontology of Spacetime, online 27 Haziran 2010 tarihinde Wayback Machine sitesinde .
- (ed.), The Ontology of Spacetime, Elsevier 2006,
- D. Malament, 1977. "Causal Theories of Time and the Conventionality of Simultaniety," Noûs 11, 293–300.
- Galison, P. (2003), Einstein's Clocks, Poincaré's Maps: Empires of Time, New York: W.W. Norton,
- A. Grünbaum. David Malament and the Conventionality of Simultaneity: A Reply, online 2 Temmuz 2010 tarihinde Wayback Machine sitesinde .
- S. Sarkar, J. Stachel, Did Malament Prove the Non-Conventionality of Simultaneity in the Special Theory of Relativity?, Philosophy of Science, Vol. 66, No. 2
- H. Reichenbach, Axiomatization of the theory of relativity, Berkeley University Press, 1969
- H. Reichenbach, The philosophy of space & time, Dover, New York, 1958
- H. P. Robertson, Postulate versus Observation in the Special Theory of Relativity, Reviews of Modern Physics, 1949
- R. Rynasiewicz, Definition, Convention, and Simultaneity: Malament's Result and Its Alleged Refutation by Sarkar and Stachel, Philosophy of Science, Vol. 68, No. 3, Supplement, online 29 Haziran 2010 tarihinde Wayback Machine sitesinde .
- Hanoch Ben-Yami, Causality and Temporal Order in Special Relativity, British Jnl. for the Philosophy of Sci., Volume 57, Number 3, pp. 459–479,
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Einstein senkronizasyonu veya Poincare Einstein senkronizasyonu farkli yerlerdeki saatlerin sinyal degisimleri vasitasiyla senkronize edilmesi yontemidir Bu senkronizasyon yontemi halihazirda 19 yuzyilin ortalarinda telegrafcilar tarafindan kullanilmistir ancak isik sinyalleri uzerine uygulayan ve gorelelik teorisindeki temel rolunu fark eden Henri Poincare ve Albert Einstein tarafindan meshur edilmistir Temel degeri tek bir eylemsiz cercevedeki saatler icindir EinsteinEinstein in 1905 teki formulune gore t1 displaystyle tau 1 aninda 1 no lu saat ten 2 no lu saat e dogru bir isik sinyali gonderiliyor ve ayni anda geri donuyor mesela bir ayna vasitasiyla isik sinyalinin 1 no lu saat e geri ulastigindaki sure ise t2 displaystyle tau 2 olsun Bu senkronizasyon yontemi 2 no lu saat in 1 no lu saatle eszamanli yapilmasi senkronizasyonu icin yapilir ve bu senkronizasyonda isin yansimasinin oldugu ana ise t3 displaystyle tau 3 diyebiliriz t3 t1 12 t2 t1 12 t1 t2 displaystyle tau 3 tau 1 tfrac 1 2 tau 2 tau 1 tfrac 1 2 tau 1 tau 2 olarak tanimlanir Ayni senkronizasyon tasima hizinin kaybolacagi kadar yavas bir limitte ucuncu bir saat i 1 no lu saat ten 2 no lu saat e tasiyarak da elde edilir Literaturde tartisilmasina ragmen saat senkronizasyonu icin pek cok fikir deneyi de ayni sonucu vermistir Sorun bu senkronizasyonun gercekten tutarli bir sekilde herhangi bir olaya bir zaman etiketi atamada barisili olup olmadigidir Bu amacla kosullari saglayan bir durum bulunmalidir a saatler bir kez senkronize edilince senkronize kalirlar b1 senkronizasyon yani her saat kendi tarafindan senkronize edilir otomatik olarak sartlari yerine getirdi b2 senkronizasyon yani eger saat A saat B ile senkronize ise saat B de saat A ile senkronizedir b3 senkronizasyon yani eger saat A saat B ile senkronize ve saat B de saat C ile senkronizeyse saat A saat C ile senkronizedir Eger a noktasi tutuyorsa o zaman saatlerin senkronize oldugunu soylemek mantiklidir Verilen a da eger b1 b3 tutuyorsa o zaman senkronizasyon kuresel zaman fonksiyonu t yi kurmamiza olanak tanir t sabit dilimler eszamanlilik dilimi olarak adlandirilir Einstein 1905 a ve b1 b3 un isigin ilerleyisinin fiziksel ozellikleriyle kolaylikla dogrulanabilecegine indirgenme ihtimalini fark etmedi Onun yerine Bu senkronizasyon taniminin celiskilerden bagimsiz oldugunu varsayalim ve her sayidaki nokta icin mumkun oldugunu ve takip eden b2 b3 iliskiler evrensel olarak gecerlidir Bu nedenle ve yeni gelismelerin pek de iyi bilinmemesinden dolayi bazi fiziksel makaleler hala gorelik kurami onermeleri arasinda Einstein senkronizasyonunun tutarliligi varsayimini sunmaktadir kaynak belirtilmeli Max Von Laue ilk kez Einstein in senkronizasyonunun tutarliligi problemini calisan kisidir L Silberstein cogu iddialarini gorelik uzerine olan kitabinda okuyucular icin alistirma olarak birakmasina ragmen benzer bir calisma sunmustur Max von Laue nin tezleri H Reichenbach and found a final shape in a work by A Macdonald tarafindan yeniden ele alindi ve A MacDonald tarafindan calismalarinda son sekline kavustu Einstein senkronizasyonunun onceki kosullari sagliyor olusunun cozumu ancak ve ancak takip eden iki kosulla karsilanir i Kirmiziya kayma olmayacak Eger A noktasindan A daki saat tarafindan kaydedilen ve Dt kadar zaman sonra iki parlama gonderilirse B deki bir saat tarafindan kaydedilmis Dt kadar zaman sonra ayri ayri B ye ulasirlar ii Reichenbach in gidis donus kosulu Eger bir isik demeti A dan baslayan ABC ucgeni uzerine gonderilirse ve B ve C deki aynalarca yansitilan bu durumda A noktasina geri donme olayi takip edilen istikametten bagimsizdir ABCA veya ACBA Bir kez saatler senkronize edilince tek yonlu isik hizini olcebilir Buna ragmen Einstein in senkronizasyonunun uygulanabilirligini garanti eden onceki kosullar tek yonlu isik hizinin her karede ayni olarak ortaya cikacagi anlamina gelmez Dusunun iii Von Laue ve Weyl s nin gidis donus kosulu L uzunlugundaki bir kapali yoldan isik isininin gecmesi icin gereken zaman L cdir Burada L yolun uzunlugu ve c de yoldan bagimsiz bir sabittir Bir teori cikis noktasi von Laue ve Weyl ye kadar takip edilebilir ancak ve ancak Einstein senkronizasyonunun surekli uygulanabilir oldugunda Laue Weyl nin gidis donus kosulunu saglar ornegin a ve b1 b3 saglar ve senkronize saatlere goreli tek yonlu isik hizi tum karelerde sabittir Laue Weyl kosulunun onemi bahsi gecen zamanin sadece bir saatle olculebilecegi gerceginin ustune kuruludur buna gore bu kosul senkronizasyon kurallarina dayanmaz ve deneysel olarak kontrol edilebilir Nitekim Laue Weyl gidis donus kosulunun sagladigi eylemsizlik cercevesinde deneysel olarak dogrulanmistir Uzak saatlerin senkronizasyonundan once tek yonlu hizi olcmek anlamsiz oldugundan tek yonlu isik hizi olcumu iddiasindaki deneylerin genelde Laue Weyl gidis donus kosullarinin yeniden yorumlanmasinin dogrulanmasi olarak gorulmesi mumkundur Einstein senkronizasyonu sadece boyle dogal gorunur Kolaylikla bunun yalnizca bir anlasma oldugu unutulabilir Donen cercevelerde ozel gorelilikte bile Einstein senkronizasyonu disi gecislilik yararliligini azaltir Eger saat 1 ve saat 2 dogrudan senkronize degilse saatler arasi bir zincir kullanilmissa senkronizasyon secilen yola baglidir Donen diskin cevresindeki senkronizasyon kullanilan yola bagli azalmayan zaman farkini verir Bu ve Ehrenfest paradoksunda onemlidir Kuresel konumlandirma sistemi GPS bu konudan etkilenir Einstein senkronizasyonunun uzlasimciliginin somut tartismalari Reichenbach a dayanir Bu senkronizasyonun alisilmisligini inkar girisimlerinin yalanlandigi kabul edilir argumanlarinin kayda deger bir haric tutulmasi ile nedensel baglantinin kuresel iliskisinden cikarilabilir Bu yerlesse de yerlesmese de konu tartismalidir Tarihce PoincareSenkronizasyonun alisilmisliginin bazi ozellikleri Henri Poincare tarafindan ongorulmustur 1898 yilinda felsefi bir makalede isik hizinin tum yonlerde sabit olmasi ilkesinin fiziksel kanunlar ile basit bir sekilde formulize edilmesinin faydasini savundu Ayrica farkli yerlerdeki olaylarin eszamanliliginin taniminin sadece bir kurali oldugunu gosterdi Bu kurallara dayanarak ama simdilerde yururlukten kaldirilmis cercevesinde 1900 yilinda Poincare saat senkronizasyonunu tanimlamak icin asagidaki kurali onerdi esir icinde hareket eden iki gozlemci A ve B saatlerini optik sinyaller araciligiyla senkronize eder Gorelilik ilkesinden oturu esirde duragan olacagina inanirlar ve isik hizinin tum yonlerde sabit olacagini kabul ederler Bu nedenle sinyallerin sadece iletim suresini goz onunde bulundurmaniz gerekir ve daha sonra gozlemcilerin gecislerini incelemesi gerekir saatleri senkronize olsun veya olmasin Cesitli noktalara yerlestirilecek bazi gozlemciler oldugunu varsayalim ve isik sinyallerini kullanarak kendi saatlerini senkronize etsinler Olculen sinyallerin iletim surelerini ayarlama girisiminde bulunurlar ancak ortak hareketlerinin farkinda degillerdir ve sonuc olarak sinyallerin esit hizla iki yonde de yolculuk edecegini dusunelim Gecis sinyallerinin gozlemlerini gerceklestirirler biri A dan B ye yol alir B den A ya farkli bir yolculukla takip edilir Ayarlanmis saatler tarafindan gosterilen t displaystyle t yerel zamandir Eger V 1K0 displaystyle V tfrac 1 sqrt K 0 isik hizi ise v displaystyle v de dunyanin hizidir ki biz onu x displaystyle x eksenine paralel kabul ediyoruz ve pozitif yonde oldugunu Boylece t t vxV2 displaystyle t t tfrac vx V 2 1904 yilinda Poincare ayni proseduru asagidaki yontemle gostermistir Optik sinyallere gore kendi saatler ayarlamak isteyen iki gozlemci dusunun sinyalleri degissinler ancak onlarin da bildigi gibi isik iletimi anlik degildir onlar gecmek icin dikkatlidir Istasyon B istasyon A nin sinyalini algiladigi zaman istasyon A nin saati sinyal gonderme aninda saat isaretlememelidir ama bu saat iletim suresini temsil eden bir sabite gore artar Varsayalim ki ornegin istasyon A saati saat 0 i isaretlediginde sinyalini gondersin ve istasyon B o sinyali algilasin ve t displaystyle t saatini isaretlesin Eger t yavaslik iletim suresini temsil ediyorsa saatler ayarlanir ve bunu dogrulamak icin istasyon B kendi sirasinda bir sinyal gonderir ve saatini 0 a isaretler sonra istasyon A algiladiginda saatini t t displaystyle t olarak isaretlemelidir Sonra kronometreler ayarlanir Ve aslinda onlar ayni fiziksel anda ayni saati isaretler ama bir sartla iki istasyon sabit oldugunda Aksi halde iletim suresi iki anlamda ayni olmaz cunku istasyon A ornegin B den kaynaklanan optik karisikligi karsilamak icin ileri gider ancak istasyon B ise A dan kaynaklanan karisiklik gelmeden once kacar Bu sekilde ayarlanmis saatler isaretlenmez bu nedenle gercek zaman isaretleme yaparlar ve bu isarete yerel zaman denir bu yuzden bunlardan biri digerinden yavas olur Kaynakca Einstein A 1905 PDF Annalen der Physik 17 10 ss 891 921 Bibcode 1905AnP 322 891E doi 10 1002 andp 19053221004 20 Subat 2005 tarihinde kaynagindan PDF arsivlendi erisim tarihi 10 Ocak 2015 See also English translation 25 Kasim 2005 tarihinde Wayback Machine sitesinde Laue M 1911 Das Relativitatsprinzip Braunschweig Friedr Vieweg amp Sohn Minguzzi E The Poincare Einstein synchronization historical aspects and new developments Phys Conf Ser cilt 306 s 012059 Bibcode 2011JPhCS 306a2059M doi 10 1088 1742 6596 306 1 012059 Silberstein L 1914 The theory of relativity Londra Macmillan Reichenbach H 1969 Axiomatization of the Theory of Relativity Berkeley University of California Press Macdonald A 1983 Clock synchronization a universal light speed and the terrestrial red shift experiment American Journal of Physics 51 9 ss 795 797 Bibcode 1983AmJPh 51 795M doi 10 1119 1 13500 Minguzzi E and Macdonald A 2003 Universal one way light speed from a universal light speed over closed paths Foundations of Physics Letters 16 6 ss 593 604 arXiv gr qc 0211091 2 Bibcode 2003FoPhL 16 593M doi 10 1023 B FOPL 0000012785 16203 52 KB1 bakim Birden fazla ad yazar listesi link Weyl H 1988 Raum Zeit Materie New York Springer Verlag Seventh edition based on the fifth German edition 1923 Galison 2002 Darrigol 2005 Poincare Henri 1898 The Measure of Time The foundations of science New York Science Press ss 222 234 Poincare Henri 1900 La theorie de Lorentz et le principe de reaction Archives neerlandaises des sciences exactes et naturelles cilt 5 ss 252 278 See also the English translation 26 Haziran 2008 tarihinde Wayback Machine sitesinde Poincare Henri 1904 The Principles of Mathematical Physics Congress of arts and science universal exposition St Louis 1904 1 Boston and New York Houghton Mifflin and Company ss 604 622 YazilarDarrigol Olivier 2005 The Genesis of the theory of relativity PDF Seminaire Poincare cilt 1 ss 1 22 doi 10 1007 3 7643 7436 5 1 8 Kasim 2018 tarihinde kaynagindan PDF erisim tarihi 12 Ocak 2015 Becoming relativity and locality in The Ontology of Spacetime online 27 Haziran 2010 tarihinde Wayback Machine sitesinde ed The Ontology of Spacetime Elsevier 2006 ISBN 0 444 52768 0 D Malament 1977 Causal Theories of Time and the Conventionality of Simultaniety Nous 11 293 300 Galison P 2003 Einstein s Clocks Poincare s Maps Empires of Time New York W W Norton ISBN 0 393 32604 7 A Grunbaum David Malament and the Conventionality of Simultaneity A Reply online 2 Temmuz 2010 tarihinde Wayback Machine sitesinde S Sarkar J Stachel Did Malament Prove the Non Conventionality of Simultaneity in the Special Theory of Relativity Philosophy of Science Vol 66 No 2 H Reichenbach Axiomatization of the theory of relativity Berkeley University Press 1969 H Reichenbach The philosophy of space amp time Dover New York 1958 H P Robertson Postulate versus Observation in the Special Theory of Relativity Reviews of Modern Physics 1949 R Rynasiewicz Definition Convention and Simultaneity Malament s Result and Its Alleged Refutation by Sarkar and Stachel Philosophy of Science Vol 68 No 3 Supplement online 29 Haziran 2010 tarihinde Wayback Machine sitesinde Hanoch Ben Yami Causality and Temporal Order in Special Relativity British Jnl for the Philosophy of Sci Volume 57 Number 3 pp 459 479