Elektromanyetik kuramı

Maxwell denklemleri Lorentz kuvveti yasası ile birlikte , ve elektrik devrelerine kaynak oluşturan bir dizi kısmi türevli (diferansiyel) denklemlerden oluşur. Bu alanlar modern elektrik ve haberleşme teknolojilerinin temelini oluşturmaktadır. Maxwell denklemleri elektrik ve manyetik alanların birbirileri, yükler ve akımlar tarafından nasıl değiştirildiği ve üretildiğini açıklamaktadır. Bu denklemler sonra İskoç fizikçi ve matematikçi olan ve 1861-1862 yıllarında bu denklemlerin ilk biçimini yayımlayan James Clerk Maxwell’ in ismi ile adlandırılmıştır.

Maxwell denklemleri iki ana değişkene sahiptir. Maxwell denklemlerinin mikroskobik biçimi atomik ölçekte malzemelerdeki karmaşık yükleri ve akımları kapsayan toplam yük ve toplam akımı kullanır. Bu denklem evrensel uygulanabilirliğe sahip olsa da hesaplama açısından olanaksız olabilmektedir. Maxwell denklemlerin mikroskobik kümesi atomik ölçekteki ayrıntıları dikkate almak zorunda kalmadan büyük ölçekteki davranışları açıklamada iki yeni yardımcı alan tanımlar, fakat ilgili maddenin elektromanyetik özelliklerini tanımlamada kullanılan parametrelere de ihtiyaç duymaktadır.

Maxwell denklemleri terimi genellikle bu denklemlerin diğer türleri için de kullanılır. Örneğin, uzay-zaman denklemleri ve kütleçekimi fiziğinde yaygın olarak kullanılır. Uzay ve zaman olarak ayrı ayrı tanımlanmaktansa uzay-zaman olarak tanımlanan bu denklemler özel ve genel görecelikle açıkça uyumludur. Nicem (Kuantum) mekaniğinde, elektrik ve manyetik potansiyellere bağlı olan Maxwell denklemlerinin türleri tercih edilir. 20. yüzyılın ortalarından beri, Maxwell eşitliklerinin kesin evren kuralı olmadığı, fakat nicel elektrodinamiğin doğru ve temel kuramına daha uygun klasik bir yaklaşım olduğu anlaşılmıştır. Birçok durumda, Maxwell denklemlerinden oluşan nicel sapmalar ölçülemeyecek kadar küçüktür. Işığın parçacık doğasının önemli olduğu ya da çok güçlü elektrik alanlarında istisnalar oluşabilir.

Elektrik ve manyetik alanlara göre denklemler

Bu denklemler içindeki elektromanyetizmayı anlatmak için, bu makalede yöney (vektör) hesabı dili kullanılmıştır. Aksi belirtilmedikçe, koyu renkle belirtilmiş semboller yöney miktarını ve yatık belirtilmiş semboller sayısal miktarını belirtmektedir. Denklemlerde, her biri genellikle zamana bağlı olan, bir yöney alanı olan elektriksel alan E ve bir yöney alan olan manyetik alanı B olarak tanıtılmıştır. Bu alanların kaynakları yük yoğunluğu ρ ve akım yoğunluğu J olarak adlandırılan bölgesel yoğunluklar olarak belirtilen elektrik yükleri ve akımlarıdır. Diğer bir doğa kanunu olan Lorentz’in kuvvet kanunu, elektrik ve manyetik alanların yüklü parçacıklar ve akımlar üzerinde nasıl etki ettiğini açıklamaktadır. Bu kanunun diğer bir türü Maxwell’in asıl eşitliğinde bulunmaktadır.

Elektrik-manyetik alan denklemlerinde dört adet denklem bulunmaktadır. Bunlardan iki tanesi, eğer Gauss yasasında olan elektrik yüklerinden kaynaklanan elektrik alanları ve Gauss’un manyetizma yasasının manyetik tekkutuplularına bağlı olmadan alan çizgilerine yakın oluşan manyetik alan var ise, kaynağa göre uzay içinde bu alanların nasıl değiştiğini açıklamaktadır. Diğer iki tanesi de Faraday yasasındaki zamanla değişken manyetik alanların etrafında “dolaşan” elektrik alanları sırasında Maxwell doğrulaması ile olan Ampere yasasındaki elektrik akımı ve zamanla değişen elektrik alanları etrafında “dolaşan” manyetik alanın oluşturmuş olduğu kişisel kaynakların çevresinde alanların nasıl “dolandığını” açıklamaktadır.

Maxwell eşitliğinin kesinliği içerdiği büyüklüklerin ne kadar kesin tanımlandığına bağlıdır. Kurallar birim sistemine göre değişir, çünkü ışık hızı gibi boyutsuz çarpanlar tarafından emilerek çeşitli tanımları ve boyutları değişebilmektedir.

Ölçü Birimlerindeki standart denklemler

Bu bölümdeki denklemler ölçü birimli geleneksel (konvansiyonel) kullanımlarda verilmiştir. Yaygın kullanılan diğer birimler CGS sistemine dayalı Gaussian birimleri, Lorentz-Heaviside birimleri (çoğunlukla parçacık fiziğinde kullanılan) ve Planck (kuramsal fizikte kullanılan) birimleridir.

Bakınız Gaussian birimli denklemler David J Griffiths (1999). Elektrodinamiğe giriş. Third. Prentice Hall. ss. 559-562. ISBN . 17 Haziran 2008 tarihinde kaynağından . Erişim tarihi: 12 Şubat 2014. </ref> (genelde parçacık fiziği) ve Planck birimleri (kullanıldı teorik fizik). bakınız below Gaussian birimleri ile ilgili denklemler için.

isim	İntegral (tümlev) denklemleri	Türev denklemleri
Gauss yasası	${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {1}{\varepsilon _{0}}}\iiint _{\Omega }\rho \,\mathrm {d} V}$	${\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}}$
Manyetizma için Gauss yasası	${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}$	${\displaystyle \nabla \cdot \mathbf {B} =0}$
Maxwell–Faraday denklemleri	${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {d}{dt}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S} }$	${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$
Ampère yasası (Maxwell denklemi ile)	${\displaystyle \oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\iint _{\Sigma }\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} }$	${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)}$

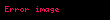
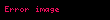
Bu denklemlerde görünen bazı evrensel sabit sayılar bulunmaktadır; boş uzayın elektrik geçirgenliği ${\displaystyle \epsilon _{0}}$, boş uzayın manyetik geçirgenliği ${\displaystyle \mu _{0}}$.

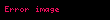
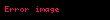
Alanların bölgesel (lokal) bir tanımı olan türev denklemlerinde, nabla sembolü ${\displaystyle \nabla }$ ile belirtilen üç boyutlu yöntürevi (gradyan) işlemcisinin ${\displaystyle \nabla \cdot }$ olanı (divergence) işlemcisini, ${\displaystyle \nabla \times }$ olanı burkulum (curl) işlemcisidir. Buradaki kaynaklar yük ve akımın bölgesel yoğunlukları olarak alınırlar.

Boş bir bölgede, alan tanımı olan tümlev denklemlerinde, ${\displaystyle \partial \Omega }$ limit yüzeyli herhangi bir sabit hacim ${\displaystyle \Omega }$, ${\displaystyle \partial \Sigma }$ limit bükeyli herhangi bir sabit açık yüzey ${\displaystyle \Sigma }$ dır. Buradaki “sabitin” anlamı zamanla değişmeyen hacim ya da yüzey demektir. Maxwell denklemi zamana bağlı hacim ve yüzeylerle denklemleştirilebilmesine rağmen, bu aslında o kadar da önemli değildir: bu denklemler zamandan bağımsız yüzeylerle tamamlanıp doğrulanmaktadır. Kaynaklar, tümlevle bulunan bu hacim ve yüzeylerin içindeki toplam yük miktarına ve akımına bağlıdır. Herhangi bir sabit hacim ${\displaystyle \Omega }$ üzerindeki toplam yük yoğunluğunun ρ hacim tümlevi, ${\displaystyle \Omega }$ içerdiği toplam elektrik yüküdür.

${\displaystyle Q=\iiint _{\Omega }\rho \,\mathrm {d} V\,,}$

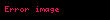
Ve herhangi bir açık sabit yüzeyden geçen elektrik akım yoğunluğunun J yüzey tümlevi net elektrik akımıdır.

${\displaystyle I=\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} \,,}$

dS yüzey alanı S türevsel yöney elementinin, yüzey Σ ye dik olarak belirtilmektedir. (yöney alanı S yerine A olarak da belirtilir, fakat bu manyetik potansiyeldeki ayırıcı yöney alanı ile çelişir.)

“Toplam yük ya da akım” serbest ve bağıl yük ya da serbest ve bağıl akım olarak da belirtilir. Bunlar aşağıda bulunan mikroskobik denklemlerde de kullanılır.

Türev ve tümlev denklemleri arasındaki ilişki

Denklemlerin türev ve tümlev denklemleri matematiksel eşitlikler olup, Gauss manyetizma kanunu ve Gauss kanunundaki (divergence teorem) ve Faraday yasası ile Ampere yasasındaki Kelvin-Stokes kuramından oluşmuştur. Hem türev hem tümlev denklemleri kullanışlıdır. Tümlev denklemleri sıkça akım ve yüklerin simetrik dağılımlarından oluşan alanların kolayca ve doğrudan hesaplanması için kullanılır. Buna karşılık, türev denklemleri, sonlu elemanlar çözümlemesindeki (analizindeki) gibi daha karmaşık (az simetrik) durumlardaki alanların hesaplanmasında daha doğal bir başlangıç noktasıdır.

Akı ve Yayılım

“Kaynaktan doğan alanlar”, sırasıyla elektrik akısı ve manyetik akı olarak tanımlanan, kapalı ${\displaystyle \partial \Omega }$ yüzeyine doğru alanın yüzey tümlevi olarak anlamlandırılabilir.

Kapalı yüzey Ω ve sınırı ∂Ω,F kuvvetini oluşturan + ve - yükü çevreler . Buradaki F kuvveti E elektrik alanından kaynaklanıyor olabilirken,herhangi bir manyetik yükü olmayan B manyetik alanından olamaz.n yüzeyden dışa doğru .

${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {E} \cdot \mathrm {d} \mathbf {S} \,,}$

${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {B} \cdot \mathrm {d} \mathbf {S} \,,}$

Kendi yayılımları gibi: ${\displaystyle \nabla \cdot \mathbf {E} ,\quad \nabla \cdot \mathbf {B} \,.}$ Bu yüzey tümlevleri ve yayılımları ile bağlantılıdır.

Dolaşım ve burkulum

Açık yüzey Σ ve sınırı ∂Σ. F kuvvetini E veya B alanı yaratıyor olabilir. n . (Bir vektör alanı aslında döngüsel görünmez,bu sezgisel bir tasvirdir).

“Alanlardaki dolaşımlar” kapalı ∂Σ eğrisi etrafındaki alanın çizgisel tümlevlerinden yorumlanabilmektedir.

${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }},\quad \oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}\,,}$

dℓ burada yol/eğriye teğet yol uzunluğunun türevsel vektör elementidir.

Aynı zamanda eğimleri,

${\displaystyle \nabla \times \mathbf {E} ,\quad \nabla \times \mathbf {B} \,.}$

Bu çizgi tümlevleri ve eğimler Stokes teoremi ile bağlantılı ve klasik sıvı dinamiklerindeki miktarlarla benzerdir.

Zaman evrimi

Dinamik ya da alanların zaman evrimi zamana bağlı alanların kısmi türevlerine göredir.

${\displaystyle {\frac {\partial \mathbf {E} }{\partial t}},\quad {\frac {\partial \mathbf {B} }{\partial t}}.}$

Bu türevler elektromanyetik dalgaların türündeki alan yayılımı tahmini çok zordur. Faraday yasasının aşağıdaki dönüşümü, yüzey zaman bağımsız olarak alındığında yapılabilmektedir.

${\displaystyle {\frac {d}{dt}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot \mathrm {d} \mathbf {S} \,,}$

İntegral işaretinin altındaki katsayının çözülmesine daha çok sonuç almak için bakınız.

Gauss yasası

Gauss yasası statik elektrik alanı ve statik elektrik alanını pozitif yükten negatif yüke doğru itilmesine neden olan elektrik yükleri arasındaki ilişkiyi tanımlamaktadır. Alan çizgisi tanımında, elektrik alan çizgileri sadece pozitif elektrik yüklerinde başlayıp, sadece negatif elektrik yüklerinde biterler. Kapalı bir alandan geçen alan çizgisi sayısını “hesaplamak”, boşluk (vakum geçirimlilikle) di-elektriksizliğinin tarafından bölünen yüzeyin çevrelediği toplam yükü (maddenin kutuplaşmasından dolayı bağıl olan yükü içeren) sağlamaktadır. Daha teknik olarak, herhangi bir farazi kapalı “Gaussian yüzeyi ”ne doğru oluşan elektrik akısı ile ilişkilidir.

manyetizma için Gauss: Manyetizma için Gauss yasası: Manyetik alan çizgilerinin başlangıcı ve sonu yoktur.Kapalı eğri şeklindedirler veya sonsuza uzarlar.

Manyetizma için Gauss yasası

Manyetizma için olan Gauss yasası elektrik yükleriyle kıyas edilebilen manyetik yükün (manyetik tek kutuplu da denilir) bulunmadığı ifade etmektedir. Bunun yerine, maddeye göre manyetik alan çift kutup denilen yapılardan oluşmuştur. Manyetik çift kutuplar en iyi akım döngüleri olarak tanımlanmaktadır, fakat net bir manyetik yüke sahip olmayan ayrılmaz bir şekilde birbirine bağlı olan pozitif ve negatif manyetik yüklere benzerler. Alan çizgilerine göre, bu eşitlik manyetik alan çizgilerinin ne başlayıp ne de bittiğini fakat döngü oluşturduğunu ya da sonsuzluğu ve geriye doğru genişlediğini belirtmektedir. Diğer bir deyişle, belirli bir hacim içine girmiş herhangi bir manyetik alan çizgisi o hacminin herhangi bir yerinden çıkmak zorundadır. Herhangi bir Gaussian yüzeyi boyunca toplam manyetik akının sıfır olduğu ya da manyetik alanın sarmal bobin gibi hareket eden yöneyli alanların eşdeğer teknik açıklamalarıdır.

Faraday yasası

In a , yüklü parçacıkların akı bir dalgalanma geçicidir, böylece elektrik elektrik şebekesi s dalgalanmalarına neden Dünya'nın atmosferindeki elektrik alanları ve Dünya'nın manyetik alanını değiştirmesidir. Sanatçının sunumu; boyutları ölçekli değildir.

Faraday yasası zamanla değişen manyetik alanların yapay elektrik alanlarını nasıl oluşturduğunu tanımlamaktadır. Bu dinamik indüksiyon elektrik alanı, durgun elektrik alanlarıyla birleştirilmediyse, manyetik alan gibi kapalı alan çizgilerine sahip olurlar. Elektromanyetik indüksiyonun bu yönü birçok elektrikli jeneratörünün çalışma prensibi olmaktadır, örneğin dönen bir mıknatıs çubuk dönme sırasında yakınındaki telde elektrik alanı oluşturabilen değişken bir manyetik alan oluşturur. (Not: Bu konuyla alakalı, Faraday yasasın olarak adlandırılan iki adet denklem vardır. Maxwell denkleminde kullanılan şekli her zaman geçerli olmasına rağmen Michael Faraday tarafından oluşturulan denklemden daha kısıtlı olmuştur.

Maxwell düzeltmeli Ampere yasası

's (1954) tarafından uygulanmıştır Ampère yasası. Each datalardan biri bit data.

Maxwell düzeltmeli Ampere yasası, manyetik alanın iki yoldan üretilebileceğini belirtmektedir: elektrik akımı yoluyla (bu gerçek “Ampere yasası ”dır) ve elektrik alanını değiştirme yoluyla (bu “Maxwell düzeltmesi” kısmıdır) Ampere yasasındaki Maxwell düzeltmesi bilhassa çok önemlidir. Bu düzeltme sadece manyetik alandaki değişimin elektrik alanının oluşmasına neden olmasını değil, elektrik alanındaki değişimin manyetik alanın oluşmasına neden olduğunu göstermektedir. Bu yüzden, bu denklemler kendini idame ettiren “elektromanyetik dalgalara” boşluk boyunca yolculuk etmelerine izin vermektedir. Akım ve yükler üzerinde yapılan çalışmalarından tahmin edilebilen elektromanyetik dalgalar için hesaplanan hız ışık hızıyla tam olarak eşleşmektedir; aslında ışık elektromanyetik yayılımın bir formudur (X-ray, radyo dalgaları gibi). Maxwell 1861 yılında elektromanyetik dalga ve ışığın arasında bir bağ olduğunu anlamış, böylelikle elektromanyetizma ve optik teorileri bir hale gelmiştir.

Boşluk Denklemleri, Elektromanyetik Dalgalar ve ışık hızı

Boşluk gibi olan yüksüz (ρ = 0) ve akımsız (J = 0) alanlarda, Maxwell denklemleri aşağıda şekilde indirgenin:

Bu 3D diyagram bir düzlem doğrusal aynı dalga denklemleri ile soldan sağa doğru dalga çoğaltım polarize olduğunu E = E₀ sin(−ωt + k ⋅ r) ve B = B₀ sin(−ωt + k ⋅ r) da gösterir.

${\displaystyle {\begin{aligned}\nabla \cdot \mathbf {E} &=0\quad &\nabla \times \mathbf {E} =\ -&{\frac {\partial \mathbf {B} }{\partial t}},\\\nabla \cdot \mathbf {B} &=0\quad &\nabla \times \mathbf {B} ={\frac {1}{c^{2}}}&{\frac {\partial \mathbf {E} }{\partial t}}.\end{aligned}}}$

Kıvrım denkleminde kıvrımı (∇×) alarak, kıvrım özdeşliğini ∇×(∇×X) = ∇(∇•X) − ∇²X alarak dalga denklemini elde ederiz:

${\displaystyle {\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}-\nabla ^{2}\mathbf {E} =0\,,\quad {\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}-\nabla ^{2}\mathbf {B} =0\,,}$

Boşluktaki ışık hızı aşağıdaki denklem ile ifade edilir:

${\displaystyle c={\frac {1}{\sqrt {\mu _{0}\varepsilon _{0}}}}=2.99792458\times 10^{8}\,\mathrm {m~s} ^{-1}}$

Göreceli elektriksel geçirgenlik εr ve geçirimlilik μr özellikleri olan maddelerde, ışığın faz hızı

${\displaystyle v_{p}={\frac {1}{\sqrt {\mu _{0}\mu _{r}\varepsilon _{0}\varepsilon _{r}}}}}$

İfade edilir ve genellikle c değerinden küçüktür.

Buna ek olarak, E ve B birbirine ve dalga yayılımı yönüne karşılıklı dik ve aynı fazdadır. Sinüzoidal düzlem dalgası bu denklemlerin özel bir çözümüdür. Maxwell denklemleri bu dalgaların fiziksel olarak boşlukta nasıl yayıldığını açıklamaktadır. Değişken manyetik alanlar Faraday yasası aracılığıyla değişken elektrik alanlarını oluşturmaktadır. Sırayla, bu elektrik alanları Maxwell düzeltmeli Ampere yasası ile değişken manyetik alanları oluşturmaktadır. Bu sonsuz döngü elektromanyetik ışınım olarak bilinen bu dalgalara c hızıyla boşluk boyunca hareket etmesine izin verir.

"Mikroskobik" ve "Makroskobik" karşılaştırması

Maxwell denklemlerinin mikroskobik değişkenleri atomsal seviyede yük ve akım içeren toplam yük ve toplam akım olarak sunulan elektrik E alanları ve manyetik B alanları olarak belirtilir. Bu kimi zaman Maxwell denkleminin genel formu ya da boşluktaki Maxwell denklemleri olarak adlandırılır. Mikroskobik değişkenleri ufak farklılıklar Maxwell denklemlerinde genellikle eşit sonuçlar çıkarttırır. "Maxwell mikroskobik denklemleri", aynı zamanda maddedeki Maxwell denklemi olarak da adlandırılır. Her iki denklem de benzer olup birbirlerini tanıtırlar.

Name	Integral (tümlev) denklemleri	Türev denklemleri
Gauss yasası	${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {D} \cdot \mathrm {d} \mathbf {S} =\iiint _{\Omega }\rho _{\mathrm {f} }\,\mathrm {d} V}$	${\displaystyle \nabla \cdot \mathbf {D} =\rho _{\mathrm {f} }}$
Manyetizma için Gauss yasası	${\displaystyle \oint _{\scriptstyle \partial \Omega }\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}$	${\displaystyle \nabla \cdot \mathbf {B} =0}$
Maxwell–Faraday denklemleri	${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {d}{dt}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S} }$	${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$
Ampère yasası (Maxwell denklemleri ile)	${\displaystyle \oint _{\partial \Sigma }\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{\Sigma }\left(\mathbf {J} _{\mathrm {f} }+{\frac {\partial \mathbf {D} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} }$	${\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{\mathrm {f} }+{\frac {\partial \mathbf {D} }{\partial t}}}$

"Mikroskobik" denklemlerin aksine, "makroskobik" denklemleri bağlı yük dışarı faktör Q_b ve akım I_b yüksüz akımları elde etmek için Q_f ve akım I_f kullanılır. Bu çarpanları aşağıdaki gibi toplam elektrik yükü ve akım bölerek yapılabilir:

${\displaystyle Q=Q_{\mathrm {f} }+Q_{\mathrm {b} }=\iiint _{\Omega }\left(\rho _{\mathrm {f} }+\rho _{\mathrm {b} }\right)\,\mathrm {d} V=\iiint _{\Omega }\rho \,\mathrm {d} V}$

${\displaystyle I=I_{\mathrm {f} }+I_{\mathrm {b} }=\iint _{\Sigma }\left(\mathbf {J} _{\mathrm {f} }+\mathbf {J} _{\mathrm {b} }\right)\cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} }$

Mikroskobik denklemlerden farklı olarak, Makroskobik denklemler bağıl yükler Qb ve akımlarının Ib serbest yük Qf ve akımlarına If bağlı eşitliklerini elde etmek için çarpanlarına ayrılırlar. Çarpanlarına ayırma işlemi toplam elektrik yük ve akımının saçılımıyla aşağıdaki gibi ifade edilir .

${\displaystyle Q=Q_{\mathrm {f} }+Q_{\mathrm {b} }=\iiint _{\Omega }\left(\rho _{\mathrm {f} }+\rho _{\mathrm {b} }\right)\,\mathrm {d} V=\iiint _{\Omega }\rho \,\mathrm {d} V}$

${\displaystyle I=I_{\mathrm {f} }+I_{\mathrm {b} }=\iint _{\Sigma }\left(\mathbf {J} _{\mathrm {f} }+\mathbf {J} _{\mathrm {b} }\right)\cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} }$

Çarpanlara ayırma işleminin yapılabilmesi için gerekli tamamlayıcı alanlar, yer değiştirme alanı D ve manyetik alan H ‘nin saptanması gerekir. Olgusal yapı denklemleri tamamlayıcı alanlar olan elektrik alanları E ve manyetik alanlar B ile doğru orantılıdır. Maxwell denklemindeki Mikroskobik ve Makroskobik değişkenlerin arasındaki farkı anlamak için yukarıdaki açıklamalara bakınız.

Bağ Yükü ve Akımı

Left: Üst ve alt kısmında gösterildiği gibi, mikroskobik dipollerin bir montaj karşı yüzey yükleri üretebildikleri şematik bir görünüşüdür. Right: Mikroskobik mevcut çevriminin bir montaj makroskopik olarak dolaşan akım döngüsünü üretmek için birlikte nasıl eklemeliyiz. Bunlar sınırları içinde, bireysel katkıları iptal etmek eğilimindedir, ancak sınırları hiçbir zaman iptal olmaz.

Elektrik alanı bir elektrik materyale uygulandığında, bu materyalin molekülleri mikroskobik elektrik dipolleri (çift kutup) oluşturarak karşılık verir – moleküllerin atomik çekirdekleri elektrik alanının yönünde ufak bir hareketlenme gösterirken, elektronlar aynı hareketlenmeyi elektrik alanının tersi yönünde yaparlar. İçerilen bütün yükler ayrı moleküllerine bağlanmış olsa da, bu hareketlilik durumu “Makroskopik bağ yükü” üretir. Örneğin, eğer her bir molekül aynı tepkiyi verirse, figürde görüldüğü gibi, yükün bu ufak hareketlenmeleri birleşerek, materyalin bir kenarında bir kat pozitif bağ yükü üretirken diğer kenarında da bir kat negatif bağ yükü üretir. Bağ yükünün en uygun tanımlaması materyalin polarizasyonu (P), bir birim hacmine düşen çift kutup momenti, olarak yapılabilir. Eğer P eşit dağılımlı (birlik) ise, yükün Makroskopik ayrılımı sadece P’nin girdiği ve ayrıldığı yüzeylerde üretilir. Düzensiz P dağılımlı ise, hacimde yük üretilir.

Benzer bir şekilde, bütün materyallerin oluşturduğu manyetik alan ile bileşenleri atom olan açısal momentum arasında ilişki vardır. Açısal hız mikroskobik döngü olan bağlantıyı öne sürer. Bu malzemenin dışında, mikroskobik döngü materyalin yüzeyindeki Makroskopik döngü farklı değildir. Özgün manyetik alan uzun mesafeler arası yol almasına rağmen, . Bu akıntı adlandırılıyor mıknatıslanma.

Bu karışık, granüllü yük ve akıntı sayesinde P M açısından Makroskopik ölçüde adlandırılır. P ve M ortalaması alınmış yüklerden ve büyük ölçüde sadece granüllü özgün atomlardan değil hatta etkili küçük çeşitli yükler çeşitli şekilde yerleştirilmiştir. Örneğin :Ortalaması hacme uygun alınmış manyetik alan ölçeğini anlamak için önemsiz olan ayrıntı Maxwell denklemleri bu ayrıntıları önemsenmemiştir.

Yardımcı alanları, polarizasyon ve mıknatıslanma

${\displaystyle \mathbf {D} (\mathbf {r} ,t)=\varepsilon _{0}\mathbf {E} (\mathbf {r} ,t)+\mathbf {P} (\mathbf {r} ,t)}$

${\displaystyle \mathbf {H} (\mathbf {r} ,t)={\frac {1}{\mu _{0}}}\mathbf {B} (\mathbf {r} ,t)-\mathbf {M} (\mathbf {r} ,t),}$

P polarizasyon alanı ve M manyetik alan mikroskobik yük ve akıntı açısından tanımlanır. Makroskopik yük yoğunluğu ρ_b ve yük yoğunluğu Jb polarizasyon ve mıknatıslanma tarafından tanımlanır.

${\displaystyle \rho _{b}=-\nabla \cdot \mathbf {P} ,}$

${\displaystyle \mathbf {J} _{b}=\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}.}$

Eğer özgür olarak nitelenirse, toplam yük ve yük yoğunluğu şu şekilde tanımlanır.

${\displaystyle \rho =\rho _{\mathrm {b} }+\rho _{\mathrm {f} },\ }$

${\displaystyle \mathbf {J} =\mathbf {J} _{\mathrm {b} }+\mathbf {J} _{\mathrm {f} },}$

D ve H olarak tanımlanan ilişki kullanılır. Bu Makroskopik Maxwell denklemi mikroskobik denklemler olarak tekrar üretilir.

Esas İlişki

Maxwell Makroskopik denklemleri kullanabilmek için, belirtilmeli yer değişimi olan D ve elektrik alanı E hatta manyetik alan H ve B. Eşit bir şekilde, ayrım yapılmalı uygulanan manyetik ve elektrik alanda bu ayrım bağlıdır polarizasyonla P ve mıknatıslanma M . Bu ayrıma esas ilişki denir. Asıl gerçek maddede, bu ilişki oldukça basit ve bu deneyi tanımlamada görevi vardır. Polarizasyon ve mıknatıslanma olmadan, bu ilişki de ve sabittir. Çünkü bağlı yük olmadığı için, toplam yük ve özgür yük eşittir

${\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} ,\quad \mathbf {H} =\mathbf {B} /\mu _{0}}$

Genellikle, doğrusal madde ile bu ilişki,

${\displaystyle \mathbf {D} =\varepsilon \mathbf {E} \,,\quad \mathbf {H} =\mu ^{-1}\mathbf {B} }$

ε geçirgen olduğu yerde vardır. Hatta bu doğrusal yük çeşitli sorunlara sahiptir. Homojen maddeler için ε ve μ madde boyunca sabitken, homojen olmayan maddeler bulunduğu maddenin yerine bağlıdır. Eş yönlü maddeler için, ε ve μ sayısalken, eş yönsüz maddeler gergidir. Maddeler genellikle ayırıcıdır bu yüzden ε ve μ EM dalga olaylarının sıklığına bağlıdır.

Genel olarak lineer olmayan malzemeler durumunda, (örneğin, doğrusal olmayan optiklere bakınız), D ve P mutlak e ile orantılı değildir. Aynı şekilde B zorunlu genel olarak, H ya da M orantılı değildir, D ve H hem E ye hem de B ye bağlıdır, yer ve zaman muhtemelen diğer fiziksel miktarları gösterir. Uygulama ayrıca serbest akım ve yük yoğunluklarının davranışlarının nasıl olduğunu E ve B muhtemel çiftinin diğer fizik miktarlarının basınç, kütle, sayı yoğunluğu ve yüklerinin hızları gibi orijinal denklemleri gösterir. Maxwell denklemlerindeki değişiklik Ohms yasasındaki formu ${\displaystyle \mathbf {J} _{f}=\sigma \mathbf {E} }$ kapsar.

Gaussian Birimlerindeki Denklemler

Gauss tane birimleri popüler bir sistem olup, bu birimler santimetre gram ikinci sisteminin bir parçasıdır. Geleneksel Cgs birimleri kullanarak değişik zaman elektrik alan olan ECGS = c-1 ESI gösterir. Bu değişen elektrik ve manyetik alanın aynı birime sahip olduğunu gösterir (SI kongresinde bu durum böyle değil: vakum EM dalgalar örn | ESI | = c | B | farklı denklemlerin boyutlu analizini yapma). Bu şekilde tanımlanan bir yük birimi kullanan vakum ε0 = 1 / (4πc), bu nedenle μ0 = 4π / C arasında geçirgenliğe izin verir. Bu değişik düzenler kullanılarak, elde edilen Maxwell denklemleri:

Littlejohn, Robert (sonbahar 2007). "Gaussian, SI ve Elektromanyetik Teorisi Birimleri içindeki diğer Sistemler" (PDF). Physics 221A, California üniversitesi, Berkeley ders notları. 11 Temmuz 2012 tarihinde kaynağından (PDF). Erişim tarihi: 6 Mayıs 2008. </ref>

Gaussian birimlerindeki denklemler

isim	Mikroskopik denklemler	Makroskopik denklemler
Gauss yasası	${\displaystyle \nabla \cdot \mathbf {E} =4\pi \rho }$	${\displaystyle \nabla \cdot \mathbf {D} =4\pi \rho _{\mathrm {f} }}$
manyetizma için Gauss yasası	${\displaystyle \nabla \cdot \mathbf {B} =0}$	mikroskopik ile aynı
Maxwell–Faraday denklemi	${\displaystyle \nabla \times \mathbf {E} =-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}}$	mikroskopik ile aynı
Ampère yasası (Maxwell uzantısı ile)	${\displaystyle \nabla \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)}$	${\displaystyle \nabla \times \mathbf {H} ={\frac {1}{c}}\left(4\pi \mathbf {J} _{\mathrm {f} }+{\frac {\partial \mathbf {D} }{\partial t}}\right)}$

Alternatif Denklemler

• Genel bir bakış için, Mathematical descriptions of the electromagnetic field. Açıklamalarına bakın.
• special relativity denklemleri için, classical electromagnetism and special relativity ve covariant formulation of classical electromagnetism bakın.
• general relativity denklemleri için Maxwell's equations in curved spacetime bakınız.
• quantum field theory, denklemleri için, quantum electrodynamics bkz.

Mikroskobik Maxwell denklemlerinin özeti değişik noktalardaki fizik gibi matematik denklemlerini acık ve kesin bir biçimde açıklamasını gösterir. Genellikle, aynı zamanda Maxwell denklemleri denir. Doğrudan bir uzay-zaman denklemleri olan Maxwell denklemleri (vektör hesabı denklemlerinde gizli simetrisini okuyan aslında görelilik teorisi için büyük bir ilham kaynağı oldu) relativistik değişmez olduğu gösterildi. Buna ek olarak, potansiyellerini kullanarak denklemlerle bağlantısal yazım başlangıç denklemlerini çözmek için uygun bir yol olarak kullanılır ama alanlarında bulunan tüm gözlemlenebilir fiziği ile tanıtılır. Nicem mekaniğinin merkezinde oynadığı olası oyun ve nicem mekaniğinin olası sonuçları zamanla kaybolur. Her denklem detayları için ana makalelere bakın. SI birimleri boyunca kullanılır.

denklemlemesi	denklem	Homojen denklemler	homojen olmayan denklemler
	Fields 3D Euclidean space + time	${\displaystyle \nabla \cdot \mathbf {B} =0}$ ${\displaystyle \nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}=0}$	${\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}}$ ${\displaystyle \nabla \times \mathbf {B} -{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}=\mu _{0}\mathbf {J} }$
	Potentials (any ) 3D Euclidean space + time	${\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} }$ ${\displaystyle \mathbf {E} =-\mathbf {\nabla } \varphi -{\frac {\partial \mathbf {A} }{\partial t}}}$	${\displaystyle \nabla ^{2}\varphi +{\frac {\partial }{\partial t}}\left(\mathbf {\nabla } \cdot \mathbf {A} \right)=-{\frac {\rho }{\varepsilon _{0}}}}$ ${\displaystyle \Box \mathbf {A} +\mathbf {\nabla } \left(\mathbf {\nabla } \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)=\mu _{0}\mathbf {J} }$
	Potentials () 3D Euclidean space + time	${\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} }$ ${\displaystyle \mathbf {E} =-\mathbf {\nabla } \varphi -{\frac {\partial \mathbf {A} }{\partial t}}}$ ${\displaystyle \mathbf {\nabla } \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}=0}$	${\displaystyle \Box \varphi ={\frac {\rho }{\varepsilon _{0}}}}$ ${\displaystyle \Box \mathbf {A} =\mu _{0}\mathbf {J} }$
		${\displaystyle \partial _{[\alpha }F_{\beta \gamma ]}=0}$	${\displaystyle \partial _{\alpha }F^{\beta \alpha }=\mu _{0}J^{\beta }}$
	Potentials (any gauge)	${\displaystyle F_{\alpha \beta }=\partial _{[\alpha }A_{\beta ]}}$	${\displaystyle \partial _{\alpha }\partial ^{[\beta }A^{\alpha ]}=\mu _{0}J^{\beta }}$
	Potentials (Lorenz gauge)	${\displaystyle F_{\alpha \beta }=\partial _{[\alpha }A_{\beta ]}}$ ${\displaystyle \partial _{\alpha }A^{\alpha }=0}$	${\displaystyle \Box A^{\alpha }=-\mu _{0}J^{\beta }}$
	Alanlar herhangi bir uzay zamanı	${\displaystyle \partial _{[\alpha }F_{\beta \gamma ]}=\nabla _{[\alpha }F_{\beta \gamma ]}=0}$	${\displaystyle \nabla _{\alpha }({\sqrt {-g}}F^{\beta \alpha })=\mu _{0}J^{\beta }}$
	Potensiyeller (any gauge) any space-time	${\displaystyle F_{\alpha \beta }=\partial _{[\alpha }A_{\beta ]}=\nabla _{[\alpha }A_{\beta ]}}$	${\displaystyle \nabla _{\alpha }({\sqrt {-g}}\nabla ^{[\beta }A^{\alpha ]})=\mu _{0}J^{\beta }}$
	Potensiyeller (Lorenz gauge) any space-time	${\displaystyle F_{\alpha \beta }=\partial _{[\alpha }A_{\beta ]}=\nabla _{[\alpha }A_{\beta ]},}$ ${\displaystyle \nabla _{\alpha }A^{\alpha }=0}$	${\displaystyle \Box A^{\alpha }-R_{\ \beta }^{\alpha }A^{\beta }=-\mu _{0}J^{\alpha }}$
	Alanlar any space-time	${\displaystyle \mathrm {d} F=0}$	${\displaystyle \mathrm {d} *F=\mu _{0}J}$
	Potensiyeller (any gauge) any space-time	${\displaystyle F=\mathrm {d} A}$	${\displaystyle \mathrm {d} *\mathrm {d} A=\mu _{0}J}$
	Potensiyeller (Lorenz gauge) any space-time	${\displaystyle F=\mathrm {d} A}$ ${\displaystyle \mathrm {d} \star A=0}$	${\displaystyle \star \Box A=\mu _{0}J}$

-Öklid uzayında + zamanında vektör denkleminde, ${\displaystyle \varphi }$ elektrik potansiyeli, ${\displaystyle \mathbf {A} }$ vektör potansiyeli ve${\displaystyle \Box ={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}}$ D'Alembert operator üdür.

• Gergi hesabı denkleminde, elektromanyetik gergi ${\displaystyle F_{\alpha \beta }}$ bir anti simetrik bildirdiğinden rütbe 2 gergi olduğunu, dört potansiyel ${\displaystyle A_{\alpha }}$ geçerli ${\displaystyle J^{\alpha }}$ bir vektör yoğunluğu, köşeli ayraç olan, bir bildirdiğinden vektör [] endeksleri anti simetrik olduğunu temsil eder. ${\displaystyle \partial _{\alpha }}$ koordinatları ${\displaystyle x^{\alpha }}$ göre türevidir. Minkowski üzerinde uzay koordinatlar bir atalet çerçeveye göre seçilir; ${\displaystyle (x^{\alpha })=(ct,x,y,z)}$, böylece yükseltmek ve alt endeksleri olan ${\displaystyle \eta _{\alpha \beta }=\mathrm {diag} (1,-1,-1,-1)}$ kullanılan metrik gergi ${\displaystyle \Box =\partial _{\alpha }\partial ^{\alpha }}$ dır. Genel uzay-zamanları, sistem ${\displaystyle x^{\alpha }}$, kovaryant türev ${\displaystyle \nabla _{\alpha }}$, Ricci gergi ${\displaystyle R_{\alpha \beta }}$ yükseltilmesi ve endeksleri düşürücü Lorentz metrik${\displaystyle g_{\alpha \beta }}$ tarafından ${\displaystyle \Box =\nabla _{\alpha }\nabla ^{\alpha }}$ olarak tanımlanır.
• Herhangi bir farklı uzay form denkleminde, ${\displaystyle F=F_{\alpha \beta }dx^{\alpha }\wedge dx^{\beta }}$ iki form, ${\displaystyle A=A_{\alpha }dx^{\alpha }}$ potansiyel elektromanyetik gergi olduğunu gösterir. 1 formu, J, 3 formu d dış türev ve ${\displaystyle J}$, yıldız Hodge yıldız uzay-zamanın Lorentz metrik tarafından tanımlanan formlar (iki formlar üzerinde hodge ${\displaystyle *,\star }$. Sadece bağlıdır olan akım (pseudo) bir yerel bir ölçek yani için metrik kadar) konfor mal değişmez olduğunu gösterir. Operatör ${\displaystyle \Box =(-\star \mathrm {d} *\mathrm {d} +\mathrm {d} \star \mathrm {d} \star )}$ 1-formları d'Alembert-Laplace-Beltrami operatörüdür.

Diğer denklemler geometrik cebir denklemlerle bağlantısal yazılımlarını ve Maxwell denklemlerinin bir matris temsilini içerir. Tarihsel olarak, kuaterniyonik denklemdir ilimleri [8] [9] kullanıldı.

Çözümler

Maxwell eşitliklerinde elektrik ve manyetik alanlarla ilgili ve giderleri ve akımları elektrikli olanlar için kısmi diferansiyel denklemler vardır. Genellikle, giderler ve akımlar kendilerini elektrik ve manyetik alanları üzerinden Lorentz kuvvet denklemine ve yapısal denklemlerine bağlıdır. Tüm bunlar birleştiğinde bir takım çözülmesi zor kısmi diferansiyel denklemleri çıkar. Aslında bu denklemlerin çözümleri klasik elektromanyetizma ve tüm sahada tüm farklı olguları kapsar. Herhangi bir diferansiyel denklemi gibi, sınır şartları ve başlangıç koşulları eşsiz bir çözüm için gerekli olanlardır. Örneğin, uzay zamanında hiçbir akım ve gider olmadığında bile Maxwell denklemleri ile çözümler mümkündür ama birçok çözüm bariz çözüm değildir E = B = 0. Diğer çözüm E=sabit, B=sabit, yine başka bir çözüm elektromanyetik uzay zamanı dalgalarına sahiptir. Bazı durumlarda, Maxwell denklemleri sonsuz boşluklar boyunca çözülür ve sınırlı denklemler sonsuzda kavuşmaz limit olarak verilmektedir. Diğer durumlarda, Maxwell denklemleri o bölgeye uygun sınır koşulları ile alanı sadece sınırlı bir bölge ile çözülüyor. Örneğin, sınır evrenin veya periodik sınır koşullarının dış dünyadan kalan küçük bir bölgeyi izole duvarları ile tarif ve temsil eden yapay bir emici sınır olurdu.

Jefimenko’nun denklemleri manyetik ve elektrik alanlarında yaratılan gider ve akım rahatsızlıklarının oluşturduğu Maxwell denklemlerine çözüm göstermiştir. Bu mevcut tek alanlar yükleri yoluyla oluşturulan olanlardır ve engelli çözelti olarak adlandırılan çözelti elde etmek için özel başlangıç şartlarını kabul edilmiştir. Yükleri ve akıntılar oluşturdukları alanların kendileri tarafından oluşturulduğu zaman Jefimenko’nun denklemleri pek işe yaramaz. Diferansiyel denklemler için sayısal yöntemler tam bir çözüm imkânsız olduğunda Maxwell denklemlerinden yararlanılabilir. Bu yöntemler genellikle bir bilgisayar gerektirmez ve sonlu elemanlar yöntemi ve sonlu fark zaman alanı yöntemini içerir. Maxwell denklemleri altı bilinmeyenli olarak belirtilmiştir. Üç bileşen E ve B oluşur ve iki denklem için Gauss yasasınu, üç vektör bileşeni için Faraday ve ampere yasasından yararlanılmıştır. (giderleri ve akımları bilinmemektedir.) bu Maxwell denklemlerindeki sınırı belli fazlalıklarla ilgilidir. Sayısal algoritma iki Gauss yasalarında göz ardı etmek mümkün olmasına rağmen, kötü tahmin hesaplamaları bu yasaların ihlallerine neden olur. Bu ihlalleri karakterize kukla değişkenleri tanıtarak, dört denklem yine de sonucu belirtememiş. Oluşan denklemler hesabına göre dört yasaları almak daha doğru algoritmalara yol açabilir.

Elektromanyetik Bir Çözüm İçin Formüller

Maxwell denklemleri olayların çeşitli açıklayan ve tahmin de olağanüstü başarılı iken, onlar için evrenin yasaları kesin değil sadece yaklaşıktır. Örnekler son derece güçlü alanları ve son derece kısa mesafeleri içerir. Ayrıca Maxwell denklemlerinin olanaksız olduğu tahmin edilmesine rağmen dünyada çeşitli görüngü oluşmuştur. Örnek olarak klasik olmayan ışık ve elektromanyetik alanın nicem engeli verilebilir. Son olarak, Maxwell denklemleri tam olarak sıfır olursa herhangi bir olağanüstü olaylar bireysel foton içeren durumlarda: örneğin fotoelektrik etti, Planc’s yasası, Duane-hunt yasası, tek foton ışık detektörü vb. açıklamak hem imkânsız ve zordur çünkü Maxwell denklemleri foton içermez. Tüm durumlarda en doğru tahminler için, Maxwell denklemleri ve nicem elektrodinamik yerini edilmiştir.

Değişimler

Elektromanyetik alanların bir klasik teorisi olarak bilinen Maxwell denklemlerinin popüler varyasyonları nispeten sınırlıdır çünkü standart denklemler oldukça iyi durumda durmaktadır.

Manyetik Tek Kutuplar

Maxwell denklemleri evrende elektrik yükünün olduğunu ama manyetik yükünün bulunmadığını varsayar. Gerçekte manyetik yük gözlenememiş ve var olmamıştır. Eğer bunlar var olmuş olsaydı Gauss ve Faraday kânununların değişmesi gerekebilirdi ve çıkan dört denklem elektrik ve manyetik alanların değişimi altında tamamen simetrik olacaktı (Ancak evren oluşurken kısa bir dönem için manyetik tek kutupların ortaya çıktığı düşünülmektedir).

Popüler Kültür

Maxwell denklemleri fizikçiler arasında popüler olan konulardan biridir. Bazı insanlar klasik fizik ve din arasında bir köprü kurar. Elektromanyetik denklemler ışık ile ilgilidir. Hristiyan inancında İncil'in yaratılış kısmında (Genesis 01:03) "Ve tanrı söyledi 'ışık olsun' ve ışık oluştu (And God said, “Let there be light,” and there was light.) sözü geçtiği için bu denklemlerin Tanrı ile ilgili olduğu düşünülmektedir. Resimde benzer bir t-shirt görüyoruz ve bu t-shirt Amerikan Sitcomun ‘After the Fire’ bölümünde ‘Alex’ tarafından giyilmiştir.

Kaynakça

1. ^ . 29 Aralık 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Ocak 2015.