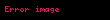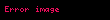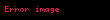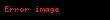Fermat ilkesi, Fermat prensibi ya da en az süre prensibi, Pierre de Fermat tarafından ışık yollarının belirlenmesi için kullanılabilen genel bir ilke. Fermat ilkesine göre bir ışık ışını herhangi iki nokta arasında ilerlerken, izlediği yol en az zamanı gerektiren yoldur.
 | |
| Optik | |
| Işığın doğası | |
|---|---|
| Işık | |
| Işık hızı | |
| Huygens-Fresnel ilkesi | |
| Fermat ilkesi | |
| Optik aygıtlar | |
| Ayna | |
| Mercek | |
| Prizma | |
| Büyüteç | |
| Kamera | |
| Mikroskop | |
| Teleskop | |
| Lazer | |
| Göz | |
| Olaylar | |
| Yansıma | |
| Tam yansıma | |
| Kırılma | |
| Saçılma | |
| Girişim | |
| Kırınım | |
| Polarizasyon | |

Bu prensip bazen ışık demetinin tanımı olarak görülür. Ancak bu tanım genel değildir, ışık demetleri yolun değişkenlerine bağlı olan sabit optikal uzunluğu kateder tanımı daha modern bir tanımdır. Bir başka deyişle, bir ışık demeti iki yanında başka yollarında olduğu neredeyse aynı sürede alabileceği bir yol tercih eder. Fermat ilkesi, aynadan yansıtılan ışığın, farklı ortamlarda kırılan ışığın ya da süregelen toplam iç yansımalardan oluşan ışığın özelliklerini tanımlamak için kullanılabilir. Fermat ilkesi, Huygen prensibi tarafından matematiksel olarak takip edilir. (küçük dalga boyları sınırında). Fermat'ın Analyse des réfractaions Snell yasası ve yansıma yasasını elde etmek için yeterlilik tekniğinden yararlanır. Fermat prensibi Hamilton prensibi ve Hamiltonian optiğiyle aynı forma sahiptir.
Modern versiyon
Elektromanyetik dalganın A ve B noktaları arasındaki yolu alması için geçen süre olan T;
“c ışık vakumdaki hızıdır”,”ds ışın üzerinde son derece küçük uzaklıktır”, v = ds/dt bir madde içindeki ışığın hızı ve n = c/v bu maddenin kırıcı dizini. Bir ışının A noktasından B noktasına olan optiksel uzunluğu şöyle tanımlanır;
Ve bu alınan yol ile ilgili S = cT' şeklinde ilgilidir'. Optiksel yol uzunluğu tamamıyla geometriksel niceliktir çünkü zaman optiksel yolun hesaplamalarında düşünülmez. A ve B noktaları arasında yol alan ışğın zamanındaki bir uç değer, bu noktalar arasındaki bir uç değerine eşittir. Fransız matematikçi Pierre de Fermat tarafından önerilen tarihsel formu tamamlanmamıştır. {{quote|İki sabit A ve B noktaları arasında ışık tarafından takip edilen yolun optiksel uzunluğu bir uç değer cümlesi varyasyonları olan Fermat prensibinin modern ve tam cümlesidir. Optiksel uzunluk fiziksel uzaklık çarpı maddenin yansıtıcı dizini olarak tanımlanır. değişkenlerin hesabının varyasyonlarının içeriğinde bu şöyle yazılabilir:
Genelde,yansıtıcı dizin uzayda bir sayısal alan pozisyonudur; 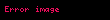
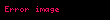
where
Bu aynı zamanda Hamilton prensibiyle aynı forma sahiptir fakat but x3 klasik mekanikte zamanın rolünü alır. Fonksiyon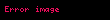
Köken
Klasik olarak Fermat’ın prensibi Huygen prensibinin matematiksel sonucu olarak düşünülebilir. Gerçekte, uç noktaları olan sabit yollara sahip bütün ikincil dalgalar (bütün muhtemelen yollar boyunca) yapıcı girişimler etkisiyle katkı sağlar. Işığın A dan B ye başta tüm muhtemel geometriksel ve fiziksel optik kurallarıyla sınırlanmamış güzergahlarda türediğini varsayalım ABj,. Çeşitli optiksel yollar ABj fazla olan dalga boyu miktarıyla birlikte değişecektir ve B ye ulaşan dalga daha fazla çeşitli aşamaya sahip olacaktır ve yıkıcı bir şekilde karışmaya daha fazla eğilimli olacaktır. Fakat eğer kısa bir yol rota varsa B AB0 ve optiksel yol bu yol üzerinde düzgünce değişiyorsa, AB0 ye yakın önemli sayıda komşu yollar AB0 densadece ikinci sıra miktarı olarak farklı optiksel yollara sahip olacaktır, bu yüzden yapıcı şekilde karışacaklardır. Bu kısa rotaya yakın ve bu rota boyunca olan dalgalar hakim olacaktır ve AB0 ışığın aldığı yol olacaktır. Herhangi parçacık (örneğin proton ya da elektron) bütün mevcut olan kapatılmış yollar üzerinde türediğini ve dalga fonksiyonun bütün bu yolar üzerinde girişimi(toplam ya da superpozisyon)(gözlemcinin ya da dedektörün noktalarında ) bu parçacığın olası doğru algılamalarını verdiğini(bu noktada) anlatan Fermat prensibi kuantum elektrodinamiğinin başlıca prensibidir. Böylece, uç yollar (en kısa,en uzun ya da sabit) bu girişime birbirlerine sıfırlamadan yapabilecekleri en çok şekilde katkı sağlarlar. Dalgaların klasik mekaniğinde Fermat prensibini mekaniğin ekstremum prensibi takip eder.
Tarihi
(Heron) (c. 60) A noktasından B noktasına giden bir ışık demeti birçok düz ayna yansımalarına uğrar ve aynı ortamda yakınındaki herhangi bir yoldan küçük bir yola sahip olduğunu anlatan yansıma prensibini tanımladı. İbni Heysem(Ibn al-Haytham-Alhacen), (1021) adlı kitabında, yansıma ve kırınım prensiplerini genişletti ve en kısa süre prensibinin ilk versiyonunu ifade etti. Onun deneyleri yunan bilim adamının Ptolemy yansıma üzerindeki çalışmalarına dayanıyordu. En az süre prensibinin genelleştirilmiş hali Fermat tarafından yazılan 1 ocak 1662 tarihli bir mektupta Cureau de la Chambre ‘ye beyan edildi. Mayıs 1662 de bu mektup optik alanında uzman olan ve o sıralar kartezyen için sözcülere öncülük eden Claude Clersselier’in itirazlarına maruz kaldı. Clerselier şunu ifade eder:
... Fermat prensibi bir neden olamaz, aksi hali olduğu halde biz bilgiyi doğaya atfetmiş olurduk ve bu durumda doğa sayesinde bizi yasallık ve dünyadaki bilgi dahilinde olmayan ve bir seçenek olmayan düzenin gerekli bir belirleme olduğunu anlıyoruz.
:
Orijinal Mahoney’den olan Fransızcası şöyledir;
Le principe que vous prenez pour fondement de votre démonstration, à savoir que la nature agit toujours par les voies les plus courtes et les plus simples, n’est qu’un principe moral et non point physique, qui n’est point et qui ne peut être la cause d’aucun effet de la nature.
Gerçekte, Fermat ilkesi tek başına var olamaz, Fermat prensibi Huygen prensibinden türetilebilir. Tarihsel olarak, Fermat ilkesi fiziksel yasaların değişken hesaplarına rehberlik eden bir prensiptir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fermat ilkesi Fermat prensibi ya da en az sure prensibi Pierre de Fermat tarafindan isik yollarinin belirlenmesi icin kullanilabilen genel bir ilke Fermat ilkesine gore bir isik isini herhangi iki nokta arasinda ilerlerken izledigi yol en az zamani gerektiren yoldur OptikIsigin dogasiIsikIsik hiziHuygens Fresnel ilkesiFermat ilkesiOptik aygitlarAynaMercekPrizmaBuyutecKameraMikroskopTeleskopLazerGozOlaylarYansimaTam yansimaKirilmaSacilmaGirisimKirinimPolarizasyon Bu prensip bazen isik demetinin tanimi olarak gorulur Ancak bu tanim genel degildir isik demetleri yolun degiskenlerine bagli olan sabit optikal uzunlugu kateder tanimi daha modern bir tanimdir Bir baska deyisle bir isik demeti iki yaninda baska yollarinda oldugu neredeyse ayni surede alabilecegi bir yol tercih eder Fermat ilkesi aynadan yansitilan isigin farkli ortamlarda kirilan isigin ya da suregelen toplam ic yansimalardan olusan isigin ozelliklerini tanimlamak icin kullanilabilir Fermat ilkesi Huygen prensibi tarafindan matematiksel olarak takip edilir kucuk dalga boylari sinirinda Fermat in Analyse des refractaions Snell yasasi ve yansima yasasini elde etmek icin yeterlilik tekniginden yararlanir Fermat prensibi Hamilton prensibi ve Hamiltonian optigiyle ayni forma sahiptir Modern versiyonElektromanyetik dalganin A ve B noktalari arasindaki yolu almasi icin gecen sure olan T T ABdt 1c ABcvdsdtdt 1c ABnds displaystyle T int mathbf A mathbf B dt frac 1 c int mathbf A mathbf B frac c v frac ds dt dt frac 1 c int mathbf A mathbf B n ds c isik vakumdaki hizidir ds isin uzerinde son derece kucuk uzakliktir v ds dt bir madde icindeki isigin hizi ve n c v bu maddenin kirici dizini Bir isinin A noktasindan B noktasina olan optiksel uzunlugu soyle tanimlanir S ABnds displaystyle S int mathbf A mathbf B n ds Ve bu alinan yol ile ilgili S cT seklinde ilgilidir Optiksel yol uzunlugu tamamiyla geometriksel niceliktir cunku zaman optiksel yolun hesaplamalarinda dusunulmez A ve B noktalari arasinda yol alan isgin zamanindaki bir uc deger bu noktalar arasindaki bir uc degerine esittir Fransiz matematikci Pierre de Fermat tarafindan onerilen tarihsel formu tamamlanmamistir quote Iki sabit A ve B noktalari arasinda isik tarafindan takip edilen yolun optiksel uzunlugu bir uc deger cumlesi varyasyonlari olan Fermat prensibinin modern ve tam cumlesidir Optiksel uzunluk fiziksel uzaklik carpi maddenin yansitici dizini olarak tanimlanir degiskenlerin hesabinin varyasyonlarinin iceriginde bu soyle yazilabilir dS d ABnds 0 displaystyle delta S delta int mathbf A mathbf B n ds 0 Genelde yansitici dizin uzayda bir sayisal alan pozisyonudur n n x1 x2 x3 displaystyle n n left x 1 x 2 x 3 right in 3D Simdi isigin x ekseni boyunca hareket eden bir bileseni oldugunu varsyalim3 bir isik demetinin yolu su sekilde parametrelerle ifade edilebilir s x1 x3 x2 x3 x3 displaystyle s left x 1 left x 3 right x 2 left x 3 right x 3 right ve nds ndx12 dx22 dx32dx3dx3 n1 x 12 x 22 dx3 displaystyle nds n frac sqrt dx 1 2 dx 2 2 dx 3 2 dx 3 dx 3 n sqrt 1 dot x 1 2 dot x 2 2 dx 3 wherex k dxk dx3 displaystyle dot x k dx k dx 3 Fermat prensibi simdi soyle yazilabilir dS d x3Ax3Bn x1 x2 x3 1 x 12 x 22dx3 displaystyle delta S delta int x 3A x 3B n left x 1 x 2 x 3 right sqrt 1 dot x 1 2 dot x 2 2 dx 3 d x3Ax3BL x1 x3 x2 x3 x 1 x3 x 2 x3 x3 dx3 0 displaystyle delta int x 3A x 3B L left x 1 left x 3 right x 2 left x 3 right dot x 1 left x 3 right dot x 2 left x 3 right x 3 right dx 3 0 Bu ayni zamanda Hamilton prensibiyle ayni forma sahiptir fakat but x3 klasik mekanikte zamanin rolunu alir FonksiyonL x1 x2 x 1 x 2 x3 displaystyle L left x 1 x 2 dot x 1 dot x 2 x 3 right Lagrangian and Hamiltonian un geometriksel optik formulasyonlarindan turetilebilen optiksel Lagrangiandir KokenKlasik olarak Fermat in prensibi Huygen prensibinin matematiksel sonucu olarak dusunulebilir Gercekte uc noktalari olan sabit yollara sahip butun ikincil dalgalar butun muhtemelen yollar boyunca yapici girisimler etkisiyle katki saglar Isigin A dan B ye basta tum muhtemel geometriksel ve fiziksel optik kurallariyla sinirlanmamis guzergahlarda turedigini varsayalim ABj Cesitli optiksel yollar ABj fazla olan dalga boyu miktariyla birlikte degisecektir ve B ye ulasan dalga daha fazla cesitli asamaya sahip olacaktir ve yikici bir sekilde karismaya daha fazla egilimli olacaktir Fakat eger kisa bir yol rota varsa B AB0 ve optiksel yol bu yol uzerinde duzgunce degisiyorsa AB0 ye yakin onemli sayida komsu yollar AB0 densadece ikinci sira miktari olarak farkli optiksel yollara sahip olacaktir bu yuzden yapici sekilde karisacaklardir Bu kisa rotaya yakin ve bu rota boyunca olan dalgalar hakim olacaktir ve AB0 isigin aldigi yol olacaktir Herhangi parcacik ornegin proton ya da elektron butun mevcut olan kapatilmis yollar uzerinde turedigini ve dalga fonksiyonun butun bu yolar uzerinde girisimi toplam ya da superpozisyon gozlemcinin ya da dedektorun noktalarinda bu parcacigin olasi dogru algilamalarini verdigini bu noktada anlatan Fermat prensibi kuantum elektrodinamiginin baslica prensibidir Boylece uc yollar en kisa en uzun ya da sabit bu girisime birbirlerine sifirlamadan yapabilecekleri en cok sekilde katki saglarlar Dalgalarin klasik mekaniginde Fermat prensibini mekanigin ekstremum prensibi takip eder Tarihi Heron c 60 A noktasindan B noktasina giden bir isik demeti bircok duz ayna yansimalarina ugrar ve ayni ortamda yakinindaki herhangi bir yoldan kucuk bir yola sahip oldugunu anlatan yansima prensibini tanimladi Ibni Heysem Ibn al Haytham Alhacen 1021 adli kitabinda yansima ve kirinim prensiplerini genisletti ve en kisa sure prensibinin ilk versiyonunu ifade etti Onun deneyleri yunan bilim adaminin Ptolemy yansima uzerindeki calismalarina dayaniyordu En az sure prensibinin genellestirilmis hali Fermat tarafindan yazilan 1 ocak 1662 tarihli bir mektupta Cureau de la Chambre ye beyan edildi Mayis 1662 de bu mektup optik alaninda uzman olan ve o siralar kartezyen icin sozculere onculuk eden Claude Clersselier in itirazlarina maruz kaldi Clerselier sunu ifade eder Fermat prensibi bir neden olamaz aksi hali oldugu halde biz bilgiyi dogaya atfetmis olurduk ve bu durumda doga sayesinde bizi yasallik ve dunyadaki bilgi dahilinde olmayan ve bir secenek olmayan duzenin gerekli bir belirleme oldugunu anliyoruz Orijinal Mahoney den olan Fransizcasi soyledir Le principe que vous prenez pour fondement de votre demonstration a savoir que la nature agit toujours par les voies les plus courtes et les plus simples n est qu un principe moral et non point physique qui n est point et qui ne peut etre la cause d aucun effet de la nature Gercekte Fermat ilkesi tek basina var olamaz Fermat prensibi Huygen prensibinden turetilebilir Tarihsel olarak Fermat ilkesi fiziksel yasalarin degisken hesaplarina rehberlik eden bir prensiptir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans