Bu madde, uygun değildir. (Ekim 2018) |
Teorik fizikte Feynman diagramları, bir Feynman diyagramının davranışını düzenleyen matematiksel ifadelerin resimsel sunumlar katılarak diyagram tarafından açıklandığı gibi atomaltı parçacıklarların davranışları gösterilmiştir. Bu şemalar bunları bulan adınadır, Amerikan fizikçisi Richard Feynman Nobel Ödülü kazandı ve 1948 yılında tanıttı. Atomaltı parçacıkların ilişkileri sezgisel anlamak karışık ve zor olabilir ve Feynman diagramları oldukça gizemli soyut formülün basit bir gösterimine izin verir. yazdı ki, "yüzyılın ortasından bu yana, bu diagramlar teorik fizikçiler için giderek zorlaşan kritik hesaplamalar uygulamasına yardım araçlarıdır," ve "Feynman diagramları Teorik fizikte her yönüyle neredeyse devrimdir.".kuantum alan teorisi diyagramların ilk uygulamasıdır, ayrıca, gibi diğer alanlardada kullanılabilir.
 |
Feynman Zamanda bir elektronun hareketi geriye doğru imiş gibi bir pozitron yorumu önerdi. ve böylece antiparçacıklar Feynman diyagramları ile hem uzay eksenli ve hem de bir zaman eksenli ama zaman içinde geriye doğru uzayda ileriye doğru hareket eden parçacıklar olarak yorumlanır. Teorik parçacıklar fiziği için olasılık genliği hesaplamaları gereklidir ve çok sayıda değişken üzerinde büyük kesirler ve karışık integraller kullanılabilir. Bununla birlikte düzgün bir yapıda bu integraller belki de grafik gösterimle Feynman diyagramları ile olabilir. Bir Feynman diagramı bir parçacık yolunun bir parçacık sınıfının bir katkısıdır,bu katkı ve şemada tanımlanarak bölünmüş. Daha kesin bir ifadeyle ve teknik olarak, Bir Feynman diyagramı bir katkının bir grafik temsilidir veya bir kuantum mekaniksel veya istatistiksel alan teorisinin korelasyon fonksiyonudur. Bununla birlikte kuantum alan teorisinin formülasyonunda,bir Feynman diyagramında perturbative içindeki terimler ile temsil eder .Alternatif olarak, kuantum alan teorisinin geçiş genliği sistem sınırından son duruma kadar parçacıklar veya alanlar içindeki terimler bütün olası geçmişlerin bir ağırlık toplamının gösterimidir.burada geçiş genliği sınırlar arası bir S-matrix matris elemanı ile verilir ve bu kuantum sistemin son durumudur.
Kanonik nicemleme formülasyonu
Olasılık genliği başlangıç durumu bir kuantum sisteminin bir geçişi için 
tarafından verilir.
burada 
burada 

burada 

Feynman kuralları
Diyagramlar etkileşimi Lagrange bağlıdır ve Feynman kurallarına göre çizilir. Lagrangian etkileşimi için , 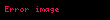


- Her entegrasyonu koordine
bir nokta tarafından gösteriliyor (bazen tepe denir);
- bozonik bir yayıcı iki noktayı birleştiren bir salınan çizgi ile temsil edilir;
- fermiyonik bir propagator iki noktayı birleştiren bir düz çizgi ile temsil edilir;
- bozonik bir alan
noktasına bağlanmış bir salınan çizgiyle temsil edilir
;
- fermiyonik bir alan
noktaya bağlı düz bir çizgi ile temsil
noktasına doğru bir ok ile;
- fermionik bir alan
noktaya bağlı düz bir çizgi
;
Örnek: QED ikinci derece süreçler
S-matris içinde ikinci dereceden pertürbasyon terimidir
Fermiyonların saçılması
Integrandı verilen Wick's açılımı (diğerleri boyunca) aşağıdaki terimler 
burada 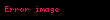
Feynman gauge içindeki elektromanyetik büzüşmedir (yayıcı). Bu terimler sağda Feynman diyagramı tarafından gösteriliyor büzülme diyagramı verilmiştir. sağdaki:
saçılma (sağdski sınır durum, son durum diyagramın solu);
saçılma (soldakisınır durum, son durum diyagramın sağı);
saçılma (alttaki sınır durum/üst, son durum diyagramda üst/alt ).
Compton saçılması ve and imha![image]() çiftini üretme
çiftini üretme
açılımdaki diğer önemli bir terim
burada
fermiyonik büzülmedir (propagator).
Elektron-pozitron imha örnekleri

The elektron-pozitron imha etkileşimi:

ikinci dereceden Feynman diyagramı amacıyla bitişik gösterilmiştir:
In the sınır durum(altındaki; yakın zaman) burada bir elektrondur(e−) ve bir positron (e+) ve final durumu(üstteki;geç zaman) burada iki foton(γ)dur.
Ayrıca bakınız
- Yayıcılar
- –Jython / Python kullanarak Feynman diyagramları çizimi için bir Java programı
- Feynman diyagramları listesi
Notlar
- ^ ""Physics and Feynman's Diagrams" by David Kaiser, American Scientist, Volume 93, p. 156" (PDF). 31 Ekim 2017 tarihinde kaynağından (PDF). Erişim tarihi: 6 Ekim 2013.
- ^ Feynman, Richard (1949). "The Theory of Positrons". Physical Review. 76 (76). s. 749. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
Kaynakça
- Gerardus 't Hooft, Martinus Veltman, Diagrammar, CERN Yellow Report 1973, online19 Mart 2005 tarihinde Wayback Machine sitesinde .
- David Kaiser, Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics, Chicago: University of Chicago Press, 2005.
- Martinus Veltman, Diagrammatica: The Path to Feynman Diagrams, Cambridge Lecture Notes in Physics, (expanded, updated version of above)
- Mark Srednicki, Quantum Field Theory, online25 Temmuz 2011 tarihinde Wayback Machine sitesinde . Script (2006)
Dış bağlantılar
| Wikimedia Commons'ta Feynman diyagramı ile ilgili ortam dosyaları bulunmaktadır. |
- AMS article: "What's New in Mathematics: Finite-dimensional Feynman Diagrams" 13 Şubat 2009 tarihinde Wayback Machine sitesinde .
- supports editing Feynman diagrams directly in Wiki articles.
- Drawing Feynman diagrams with FeynDiagram 15 Ekim 2013 tarihinde Wayback Machine sitesinde . C++ library that produces PostScript output.
- using Thorsten Ohl's Feynmf LaTeX package.
- JaxoDraw15 Eylül 2007 tarihinde Wayback Machine sitesinde . A Java program for drawing Feynman diagrams.
- Bowley, Roger (2010). "Feynman Diagrams". Sixty Symbols. - University of Nottingham. 8 Mayıs 2015 tarihinde kaynağından . Erişim tarihi: 7 Ekim 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Ekim 2018 Teorik fizikte Feynman diagramlari bir Feynman diyagraminin davranisini duzenleyen matematiksel ifadelerin resimsel sunumlar katilarak diyagram tarafindan aciklandigi gibi atomalti parcaciklarlarin davranislari gosterilmistir Bu semalar bunlari bulan adinadir Amerikan fizikcisi Richard Feynman Nobel Odulu kazandi ve 1948 yilinda tanitti Atomalti parcaciklarin iliskileri sezgisel anlamak karisik ve zor olabilir ve Feynman diagramlari oldukca gizemli soyut formulun basit bir gosterimine izin verir yazdi ki yuzyilin ortasindan bu yana bu diagramlar teorik fizikciler icin giderek zorlasan kritik hesaplamalar uygulamasina yardim araclaridir ve Feynman diagramlari Teorik fizikte her yonuyle neredeyse devrimdir kuantum alan teorisi diyagramlarin ilk uygulamasidir ayrica gibi diger alanlardada kullanilabilir Bu Feynman diyagraminda bir elektron ve bir pozitron bir foton un uretilmesi mavi sine dalgasi tarafindan gosterilebilir aliyor bir kuark antikuark cifti sonrasinda antiquark isimasi bir gluon yesil helis ile gosterilebilir Feynman Zamanda bir elektronun hareketi geriye dogru imis gibi bir pozitron yorumu onerdi ve boylece antiparcaciklar Feynman diyagramlari ile hem uzay eksenli ve hem de bir zaman eksenli ama zaman icinde geriye dogru uzayda ileriye dogru hareket eden parcaciklar olarak yorumlanir Teorik parcaciklar fizigi icin olasilik genligi hesaplamalari gereklidir ve cok sayida degisken uzerinde buyuk kesirler ve karisik integraller kullanilabilir Bununla birlikte duzgun bir yapida bu integraller belki de grafik gosterimle Feynman diyagramlari ile olabilir Bir Feynman diagrami bir parcacik yolunun bir parcacik sinifinin bir katkisidir bu katki ve semada tanimlanarak bolunmus Daha kesin bir ifadeyle ve teknik olarak Bir Feynman diyagrami bir katkinin bir grafik temsilidir veya bir kuantum mekaniksel veya istatistiksel alan teorisinin korelasyon fonksiyonudur Bununla birlikte kuantum alan teorisinin formulasyonunda bir Feynman diyagraminda perturbative icindeki terimler ile temsil eder Alternatif olarak kuantum alan teorisinin gecis genligi sistem sinirindan son duruma kadar parcaciklar veya alanlar icindeki terimler butun olasi gecmislerin bir agirlik toplaminin gosterimidir burada gecis genligi sinirlar arasi bir S matrix matris elemani ile verilir ve bu kuantum sistemin son durumudur Kanonik nicemleme formulasyonuOlasilik genligi baslangic durumu bir kuantum sisteminin bir gecisi icin i displaystyle i rangle son durumuna matris elemani f displaystyle f rangle tarafindan verilir Sfi f S i displaystyle S fi langle f S i rangle burada S displaystyle S tir kanonik kuantum alan teorisinde Lagrangian etkilesimin kuvveti bir perturbasyon serisi tarafindan S matris ile gosterilir S n 0 inn j 1nd4xjT j 1nLv xj n 0 S n displaystyle S sum n 0 infty i n over n int prod j 1 n d 4 x j T prod j 1 n L v x j equiv sum n 0 infty S n burada Lv displaystyle L v Lagrangian etkilesimdir ve T displaystyle T operatorler zaman sirali urun anlamina gelir T j 1nLv xj allpossiblecontractions N j 1nLv xj displaystyle T prod j 1 n L v x j sum mathrm all possible contractions pm N prod j 1 n L v x j burada N displaystyle N operatorler normal urun anlamina gelir ve displaystyle pm olasi isaret degisikligi fermiyonik operatorlerin gidip gelmesi icin bir buzulme biryayici bir araya getirmekle ilgilenir Feynman kurallari Diyagramlar etkilesimi Lagrange baglidir ve Feynman kurallarina gore cizilir Lagrangian etkilesimi icin Lv gps gmpsAm displaystyle L v g bar psi gamma mu psi A mu Bir fermiyonik alaninin etkilesimini tarif etmektedir ps displaystyle psi Bir bozonik gauge alani ile Am displaystyle A mu Feynman kurallari asagidaki koordinat uzayinda formule edilebilir Her entegrasyonu koordinexj displaystyle x j bir nokta tarafindan gosteriliyor bazen tepe denir bozonik bir yayici iki noktayi birlestiren bir salinan cizgi ile temsil edilir fermiyonik bir propagator iki noktayi birlestiren bir duz cizgi ile temsil edilir bozonik bir alan Am xi displaystyle A mu x i noktasina baglanmis bir salinan cizgiyle temsil edilir xi displaystyle x i fermiyonik bir alan ps xi displaystyle psi x i noktaya bagli duz bir cizgi ile temsil xi displaystyle x i noktasina dogru bir ok ile fermionik bir alan ps xi displaystyle bar psi x i noktaya bagli duz bir cizgi xi displaystyle x i Ornek QED ikinci derece surecler S matris icinde ikinci dereceden perturbasyon terimidir S 2 ie 22 d4xd4x Tps x gmps x Am x ps x gnps x An x displaystyle S 2 ie 2 over 2 int d 4 x d 4 x T bar psi x gamma mu psi x A mu x bar psi x gamma nu psi x A nu x Fermiyonlarin sacilmasi Integrandi verilen Wick s acilimi digerleri boyunca asagidaki terimler Nps x gmps x ps x gnps x Am x An x displaystyle N bar psi x gamma mu psi x bar psi x gamma nu psi x underline A mu x A nu x burada Am x An x d4k 2p 4 igmnk2 i0e ik x x displaystyle underline A mu x A nu x int d 4 k over 2 pi 4 ig mu nu over k 2 i0 e ik x x Feynman gauge icindeki elektromanyetik buzusmedir yayici Bu terimler sagda Feynman diyagrami tarafindan gosteriliyor buzulme diyagrami verilmistir sagdaki e e displaystyle e e sacilma sagdski sinir durum son durum diyagramin solu e e displaystyle e e sacilma soldakisinir durum son durum diyagramin sagi e e displaystyle e e sacilma alttaki sinir durum ust son durum diyagramda ust alt Compton sacilmasi ve and imhae e displaystyle e e ciftini uretme acilimdaki diger onemli bir terim Nps x gmps x ps x gnps x Am x An x displaystyle N bar psi x gamma mu underline psi x bar psi x gamma nu psi x A mu x A nu x burada ps x ps x d4p 2p 4igp m i0e ip x x displaystyle underline psi x bar psi x int d 4 p over 2 pi 4 i over gamma p m i0 e ip x x fermiyonik buzulmedir propagator Elektron pozitron imha ornekleri Elektron Pozitron imhasinda Feynman Diagrami The elektron pozitron imha etkilesimi e e 2g displaystyle e e to 2 gamma ikinci dereceden Feynman diyagrami amaciyla bitisik gosterilmistir In the sinir durum altindaki yakin zaman burada bir elektrondur e ve bir positron e ve final durumu ustteki gec zaman burada iki foton g dur Ayrica bakinizYayicilar Jython Python kullanarak Feynman diyagramlari cizimi icin bir Java programi Feynman diyagramlari listesiNotlar Physics and Feynman s Diagrams by David Kaiser American Scientist Volume 93 p 156 PDF 31 Ekim 2017 tarihinde kaynagindan PDF Erisim tarihi 6 Ekim 2013 Feynman Richard 1949 The Theory of Positrons Physical Review 76 76 s 749 Bibcode 1949PhRv 76 749F doi 10 1103 PhysRev 76 749 KaynakcaGerardus t Hooft Martinus Veltman Diagrammar CERN Yellow Report 1973 online19 Mart 2005 tarihinde Wayback Machine sitesinde David Kaiser Drawing Theories Apart The Dispersion of Feynman Diagrams in Postwar Physics Chicago University of Chicago Press 2005 ISBN 0 226 42266 6 Martinus Veltman Diagrammatica The Path to Feynman Diagrams Cambridge Lecture Notes in Physics ISBN 0 521 45692 4 expanded updated version of above Mark Srednicki Quantum Field Theory online25 Temmuz 2011 tarihinde Wayback Machine sitesinde Script 2006 Dis baglantilarWikimedia Commons ta Feynman diyagrami ile ilgili ortam dosyalari bulunmaktadir AMS article What s New in Mathematics Finite dimensional Feynman Diagrams 13 Subat 2009 tarihinde Wayback Machine sitesinde supports editing Feynman diagrams directly in Wiki articles Drawing Feynman diagrams with FeynDiagram 15 Ekim 2013 tarihinde Wayback Machine sitesinde C library that produces PostScript output using Thorsten Ohl s Feynmf LaTeX package JaxoDraw15 Eylul 2007 tarihinde Wayback Machine sitesinde A Java program for drawing Feynman diagrams Bowley Roger 2010 Feynman Diagrams Sixty Symbols University of Nottingham 8 Mayis 2015 tarihinde kaynagindan Erisim tarihi 7 Ekim 2013
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State