Graham sayısı, adını 'dan alan, Ramsey teorisindeki problemlerin çözümü için üst sınır getiren büyük bir sayıdır.
Martin Gardner, Kasım 1977'de Matematiksel Oyunlar bölümünün Bilimsel Amerikan kısmında bu sayıyı açıkladığında popülaritesi hızla arttı.
1980 Guinness Rekorlar Kitabı, Graham'ın talebini tekrarladı ve onu en çok ilgi çekenler listesine ekledi. Graham sayısı, googol, googolplex gibi diğer bilinen tüm sayılardan düşünülemeyecek kadar büyüktür. Ayrıca Skewes sayısı ve da büyüktür. Gerçekten de, gözlemlenebilir evren, Graham sayısının dijital ifadesini kapsamakta çok aciz kalır. Üstelik her dijitin en az bir kadar yer kapladığı varsayılırsa bile. formunun üslü kuleleri bile bunu ifade etmekten acizdir. Hem de bu kuleler Knuth yukarı ok gösterimi kullanılarak kolayca ifade edilebilirken. Graham sayısının son on rakamları ...2464195387'dir.
Ciddi matematik ispatlarında ortaya çıkan özel tam sayılar, Graham sayısından daha büyük olarak bilinir. .
Graham problemi
Graham sayısı, matematiğin bir kolu ve Ramsey teorisi olarak bilinen şu problemle ilişkilidir:
- n boyutlu ve her köşe çiftinin bağlı olduğu
köşeli elde etmeyi hayal edin. Sonra sadece kırmızı ve siyah renkleri kullanarak bu grafiğin her bir köşesini renklendirin. Bir düzlemde bulunan 4 köşeli alt grafiğin tek renkli olması gereken renklendirmenin mümkün olan en küçük n değeri nedir?
Graham & Rothschild (1971), bu problemin bir çözümü olabileceğini gösterdi. Bilinen, açıkça tanımlanan ve çok büyük sayı olan N ile üst sınır belirlensin. N* 'ye de şöyle bir sınırlama getirelim; 6 ≤ N* ≤ N. (Knuth yukarı ok gösteriminde, 

N'den daha büyük olan G üst sınırı, 

Graham sayısını açıklama
Knuth yukarı ok gösterimi kullanılarak Graham sayısı olan G (Gardner'in Bilimsel Amerikan makalesinde açıkladığı gibi) şöyle ifade edilir:
Burada, en üst dereceden başlayarak her bir derecedeki ok sayısı, onun altındaki derecenin değeriyle şöyle ifade edilir:
Yukarı oktaki üstindis kaç tane ok olduğunu belirtir. Diğer yöntemde G 64 adımda hesaplanır: İlk adım, 3'lerin arasında dört tane yukarı ok olan g1'i hesaplamaktır. İkinci adım, 3'lerin arasında g1 tane yukarı ok olan g2'yi hesaplamaktır. Üçüncü adım, 3'lerin arasında g2 tane yukarı ok olan g3'ü hesaplamaktır ve böylece devam eder. En sonuncusu, 3'lerin arasında g63 tane yukarı ok olan G = g64'ü hesaplamaktır.
Eşdeğerlilik,
f'nin üstindisi, belirtir. Örn, f 4(n) = f(f(f(f(n)))). f fonksiyonu, fonksiyon ailesinin özel bir durumudur. 


Graham sayısının büyüklüğü
Graham sayısının muazzam boyutunun zorluğunu ifade etmek için, 64 terimden meydana gelen dizinin sadece ilkini (g1) üstel olarak ifade etmek bize birazcık yardımcı olabilir. Önce tetrasyon (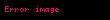
Sağdaki ifadede bulunan 3'lerin sayısı,
'dür.
Şimdi her tetrasyon (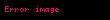

Buradan,
olur. Sadece tekrarlı "üslü kuleler" şunlardır;
ve her bir kuledeki 3'lerin sayısı, tam solundaki kuleden başlar ve sağdaki kulenin değerine eşittir.
Diğer bir yöntemler, g1 şöyle hesaplanır: Öncelikle kulelerin sayısı bulunur. n = 3^3^3^...^3 (buradaki 3'lerin sayısı 3^3^3 = 7625597484987 tanedir) Sonra n. kule şu seriye göre hesaplanır:
1. kule: 3
2. kule: 3^3^3 (3'lerin sayısı 3'dür) = 7625597484987
3. kule: 3^3^3^3...^3 (3'lerin sayısı 7625597484987'dir) = ...
. . .
g1 = n. kule: 3^3^3^3^3^3^3^...^3 (3'lerin sayısı n-1. kulenin değeri kadardır)
Ardışık her bir kuledeki 3'lerin sayısı, bir önceki kulenin değeri kadardır. Daha henüz üçüncü kulenin değeri bile n oldu.
Bu ilk g1 teriminin büyüklüğü, her ne kadar yukarıdaki gösterimlerle basitleştirilmiş olsa bile, akıl almaz derecede büyüktür. g1 için n kule sayısı Planck uzunluğundan (yaklaşık olarak 10^185 tane) bile çok büyüktür. Bu ilk terimden sonra geriye, g nin değerleri aşırı şekilde artarak çoğalan 63 tane daha terim kaldı. Graham sayısı G = g64'dir.
Graham sayısının en sağındaki rakamlar
Graham sayısı, 3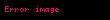
Aşağıdaki tablo d'nin birkaç değerini gösteriyor.
| Rakam sayısı (d) | 3 x x | 3 3 3 x x | 3 3 3 3 3 x x | 3 3 3 3 3 3 3 x x | 3 3 3 3 3 3 3 3 3 x x |
|---|---|---|---|---|---|
| 1 | 4 (1,3,9,7) | 2 (3,7) | 1 (7) | 1 (7) | 1 (7) |
| 2 | 20 (01,03,...,87,...,67) | 4 (03,27,83,87) | 2 (27,87) | 1 (87) | 1 (87) |
| 3 | 100 (001,003,...,387,...,667) | 20 (003,027,...387,...,587) | 4 (027,987,227,387) | 2 (987,387) | 1 (387) |
Aşağıdaki algoritma, Graham sayısının (veya 500'den daha fazla 3 içeren kulenin) en sağındaki 500 tane rakamı gösteriyor:
...02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387.
Ayrıca bakınız
Kaynakça
Dış bağlantılar
- "Geoff Exoo'nun Hiperküplerdeki bir Ramsey Problemi 20 Nisan 2010 tarihinde Wayback Machine sitesinde ."
- Mathworld maddesinde Graham sayısı 16 Şubat 2010 tarihinde Wayback Machine sitesinde .
- Graham sayısı nasıl hesaplanır 13 Şubat 2010 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Graham sayisi adini dan alan Ramsey teorisindeki problemlerin cozumu icin ust sinir getiren buyuk bir sayidir Martin Gardner Kasim 1977 de Matematiksel Oyunlar bolumunun Bilimsel Amerikan kisminda bu sayiyi acikladiginda popularitesi hizla artti 1980 Guinness Rekorlar Kitabi Graham in talebini tekrarladi ve onu en cok ilgi cekenler listesine ekledi Graham sayisi googol googolplex gibi diger bilinen tum sayilardan dusunulemeyecek kadar buyuktur Ayrica Skewes sayisi ve da buyuktur Gercekten de gozlemlenebilir evren Graham sayisinin dijital ifadesini kapsamakta cok aciz kalir Ustelik her dijitin en az bir kadar yer kapladigi varsayilirsa bile abc displaystyle a b c cdot cdot cdot formunun uslu kuleleri bile bunu ifade etmekten acizdir Hem de bu kuleler Knuth yukari ok gosterimi kullanilarak kolayca ifade edilebilirken Graham sayisinin son on rakamlari 2464195387 dir Ciddi matematik ispatlarinda ortaya cikan ozel tam sayilar Graham sayisindan daha buyuk olarak bilinir Graham problemiGraham sayisi matematigin bir kolu ve Ramsey teorisi olarak bilinen su problemle iliskilidir nboyutlu ve her kose ciftinin bagli oldugu 2n displaystyle 2 n koseli elde etmeyi hayal edin Sonra sadece kirmizi ve siyah renkleri kullanarak bu grafigin her bir kosesini renklendirin Bir duzlemde bulunan 4 koseli alt grafigin tek renkli olmasi gereken renklendirmenin mumkun olan en kucukndegeri nedir Graham amp Rothschild 1971 bu problemin bir cozumu olabilecegini gosterdi Bilinen acikca tanimlanan ve cok buyuk sayi olan N ile ust sinir belirlensin N ye de soyle bir sinirlama getirelim 6 N N Knuth yukari ok gosteriminde N F7 12 displaystyle N F 7 12 buradaki F n 2 n3 displaystyle F n 2 uparrow n 3 dur Alt sinir olan 6 Hindistan Devlet Universitesinden Geoff Exoo tarafindan 2003 yilinda 11 e yukseltildi N nin cozumu icin en iyi bilinen belirli sinir yaklasimi simdi 11 N N oldu N den daha buyuk olan G ust siniri G f64 4 displaystyle G f 64 4 olarak ifade edilir Burada f n 3 n3 displaystyle f n 3 uparrow n 3 dur Graham sayisini aciklamaKnuth yukari ok gosterimi kullanilarak Graham sayisi olan G Gardner in Bilimsel Amerikan makalesinde acikladigi gibi soyle ifade edilir G 3 33 3 3 33 3 64 derece veya seviye displaystyle left begin matrix G amp amp 3 underbrace uparrow uparrow cdots cdots cdots cdots cdots uparrow 3 amp amp 3 underbrace uparrow uparrow cdots cdots cdots cdots uparrow 3 amp amp underbrace qquad vdots qquad amp amp 3 underbrace uparrow uparrow cdots cdot cdot uparrow 3 amp amp 3 uparrow uparrow uparrow uparrow 3 end matrix right text 64 derece veya seviye Burada en ust dereceden baslayarak her bir derecedeki ok sayisi onun altindaki derecenin degeriyle soyle ifade edilir G g64 burada g1 3 3 gn 3 gn 13 displaystyle G g 64 text burada g 1 3 uparrow uparrow uparrow uparrow 3 g n 3 uparrow g n 1 3 Yukari oktaki ustindis kac tane ok oldugunu belirtir Diger yontemde G 64 adimda hesaplanir Ilk adim 3 lerin arasinda dort tane yukari ok olan g1 i hesaplamaktir Ikinci adim 3 lerin arasinda g1 tane yukari ok olan g2 yi hesaplamaktir Ucuncu adim 3 lerin arasinda g2 tane yukari ok olan g3 u hesaplamaktir ve boylece devam eder En sonuncusu 3 lerin arasinda g63 tane yukari ok olan G g64 u hesaplamaktir Esdegerlilik G f64 4 burada f n 3 n3 displaystyle G f 64 4 text burada f n 3 uparrow n 3 f nin ustindisi belirtir Orn f 4 n f f f f n f fonksiyonu fonksiyon ailesinin ozel bir durumudur f n hiper 3 n 2 3 displaystyle f n text hiper 3 n 2 3 ve Conway dizisi ok gosteriminde soyle ifade edilebilir f n 3 3 n displaystyle f n 3 rightarrow 3 rightarrow n Sonraki gosterim de G ile soyle sinirlanir 3 3 64 2 lt G lt 3 3 65 2 displaystyle 3 rightarrow 3 rightarrow 64 rightarrow 2 lt G lt 3 rightarrow 3 rightarrow 65 rightarrow 2 Graham sayisinin buyuklugu Graham sayisinin muazzam boyutunun zorlugunu ifade etmek icin 64 terimden meydana gelen dizinin sadece ilkini g1 ustel olarak ifade etmek bize birazcik yardimci olabilir Once tetrasyon displaystyle uparrow uparrow gosterimi g1 3 3 3 3 3 3 3 3 3 3 displaystyle g 1 3 uparrow uparrow uparrow uparrow 3 3 uparrow uparrow uparrow 3 uparrow uparrow uparrow 3 3 uparrow uparrow 3 uparrow uparrow 3 uparrow uparrow dots 3 uparrow uparrow 3 dots Sagdaki ifadede bulunan 3 lerin sayisi 3 3 3 3 3 displaystyle 3 uparrow uparrow uparrow 3 3 uparrow uparrow 3 uparrow uparrow 3 dur Simdi her tetrasyon displaystyle uparrow uparrow islemi bir ustel kule displaystyle uparrow azalir ve soyle olur 3 X 3 3 3 3 3 33 3burada X tane 3 var displaystyle 3 uparrow uparrow X 3 uparrow 3 uparrow 3 uparrow dots 3 uparrow 3 dots 3 3 cdot cdot cdot 3 quad text burada X tane 3 var Buradan g1 3 3 3 3 3 3lerin sayisi 3 3 3 displaystyle g 1 3 uparrow uparrow 3 uparrow uparrow 3 uparrow uparrow dots 3 uparrow uparrow 3 dots quad text 3lerin sayisi quad 3 uparrow uparrow 3 uparrow uparrow 3 olur Sadece tekrarli uslu kuleler sunlardir g1 33 3 33 3 333 3buradaki kulelerin sayisi 33 3 333 3 displaystyle g 1 left begin matrix 3 3 cdot cdot cdot cdot 3 end matrix right left begin matrix 3 3 cdot cdot cdot 3 end matrix right dots left begin matrix 3 3 3 end matrix right 3 quad text buradaki kulelerin sayisi quad left begin matrix 3 3 cdot cdot cdot 3 end matrix right left begin matrix 3 3 3 end matrix right 3 ve her bir kuledeki 3 lerin sayisi tam solundaki kuleden baslar ve sagdaki kulenin degerine esittir Diger bir yontemler g1 soyle hesaplanir Oncelikle kulelerin sayisi bulunur n 3 3 3 3 buradaki 3 lerin sayisi 3 3 3 7625597484987 tanedir Sonra n kule su seriye gore hesaplanir 1 kule 3 2 kule 3 3 3 3 lerin sayisi 3 dur 7625597484987 3 kule 3 3 3 3 3 3 lerin sayisi 7625597484987 dir g1 n kule 3 3 3 3 3 3 3 3 3 lerin sayisi n 1 kulenin degeri kadardir Ardisik her bir kuledeki 3 lerin sayisi bir onceki kulenin degeri kadardir Daha henuz ucuncu kulenin degeri bile n oldu Bu ilk g1 teriminin buyuklugu her ne kadar yukaridaki gosterimlerle basitlestirilmis olsa bile akil almaz derecede buyuktur g1 icin n kule sayisi Planck uzunlugundan yaklasik olarak 10 185 tane bile cok buyuktur Bu ilk terimden sonra geriye g nin degerleri asiri sekilde artarak cogalan 63 tane daha terim kaldi Graham sayisi G g64 dir Graham sayisinin en sagindaki rakamlarGraham sayisi 3 displaystyle uparrow uparrow formunun uslu kule sidir En sagindaki rakamlar tum benzer kuleler icin bazi ozellikler gosterir Bu ozelliklerden biri tum kulelerin yuksekligi d den daha buyuktur ve en sagdaki rakamlar ayni seriye sahiptir Bu en genel ozelliktir Tum kulelerin yuksekligi d en sagindaki rakamlar d 2 den daha buyuktur Kulenin en tepesindeki 3 bagimsizdir Ornegin en ustteki 3 en sagdaki d rakamlarini etkisinde kalmaksizin diger negatif olmayan tam sayilarla degistirilebilir Asagidaki tablo d nin birkac degerini gosteriyor 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow x degerlerinin mumkun olan farkli sayilari En sagdaki d rakamlari goz ardi edildi Rakam sayisi d 3 displaystyle uparrow x 3 displaystyle uparrow 3 displaystyle uparrow x 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow x 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow x 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow 3 displaystyle uparrow x1 4 1 3 9 7 2 3 7 1 7 1 7 1 7 2 20 01 03 87 67 4 03 27 83 87 2 27 87 1 87 1 87 3 100 001 003 387 667 20 003 027 387 587 4 027 987 227 387 2 987 387 1 387 Asagidaki algoritma Graham sayisinin veya 500 den daha fazla 3 iceren kulenin en sagindaki 500 tane rakami gosteriyor 02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387 Ayrica bakinizAckermann isleviKaynakcaDis baglantilar Geoff Exoo nun Hiperkuplerdeki bir Ramsey Problemi 20 Nisan 2010 tarihinde Wayback Machine sitesinde Mathworld maddesinde Graham sayisi 16 Subat 2010 tarihinde Wayback Machine sitesinde Graham sayisi nasil hesaplanir 13 Subat 2010 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State









