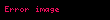Knuth yukarı ok gösterimi, matematikte, çok büyük tam sayıların gösterim yöntemidir. 1976'da Donald Knuth tarafından geliştirildi. Ackermann işlevi ve özel hiperişlem serisi ile oldukça bağlantılıdır. Çarpmanın, tekrarlı hiperişlem olarak tekrarlı toplama ve üs alma gibi görülebilmesi fikrine dayanır. Bu durumu devam ettirme tekrarlı üssü (tetrasyonu) ve çoğunlukla Knuth ok gösterimi kullanılarak ifade edilen aşırı seri üretiminin geri kalanını meydana getirir.
Tanıtım

Toplama, çarpma, üs alma gibi sıradan aritmetiksel işlemler, hiperişlem serisinde doğal olarak şöyle ifade edilir.
Bir doğal sayıyı çarpma, tekrarlı toplama olarak şöyle ifade edilebilir:
Örneğin,

Örneğin,
İşlemlerin serisini üslü gösterimden daha fazla genişleterek, tekrarlı üsleri (tetrasyonu) ifade etmek için Knuth, bir “çift ok” (operatörü) tanımladı, şöyle ki:
Örneğin,
Burada ve aşağıdaki değerlendirmede, Knuth ok işleçlerini soldan sağa doğru yerleştirme (üslü sayılarda olduğu gibi), işleçleri birleştirme olarak tanımlanır.
Bu açıklamadan,
- etc.
Bu zaten epeyce büyük bazı sayıları ifade eder. Fakat Knuth bunu gösterimle (notasyon) yaptı. Şimdi de “iki ok” işleçli (pentasyon olarak da bilinir) tekrarlı uygulamalar için “üç ok” işlecini tanıyalım:
ardından 'dört ok' işleci:
ve böyle devam eder. Genel kural, bir 

Örnekler:
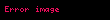


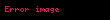
Gösterim
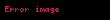


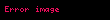
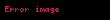
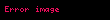
Yukarı ok gösterimini kuvvet terimleriyle yazma
Bilinen üslü gösterimi kullanarak 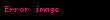
- Örneğin:
Eğer b bir değişken (veya çok büyük sayı) ise üslü kule, şu örnekte olduğu gibi, noktalar kullanarak yazılır ve kulenin yüksekliği belirtilir:
Bu gösterime devam edersek, 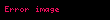
Tekrar eğer b bir değişken veya çok büyük sayı ise, yığın, nokta kullanılarak ve onun yüksekliğini belirtilerek yazılır.
Daha da arttırırsak, 
Daha genel bir ifadeyle:
Bu, 
Tetrasyonu kullanma

Son olarak dordüncü Ackermann sayısı 
Genelleştirmeler
Çok büyük sayılarda Knuth yukarı ok gösteriminin çarpım okları elverişsiz kalır. Bunun yerine n ok işleci olan 
Bazı sayılar öyle büyüktür ki gösterimler bile onları ifade etmekte aciz kalır. Graham sayısını buna örnek gösterebiliriz. Bunlar için Conway dizisi ok gösterimi kullanılabilir. Üç elemanlı bir dizi, diğer gösterimlerle eşdeğerdir. Fakat dört veya daha fazla elemanlı diziler daha kuvvetlidir.
Küçük sayılar için Knuth ok gösterimi, büyükleri için de Conway dizisi veya hiperişlemlerin kullanılması tavsiye edilir.
Açıklama


Tüm yukarı ok işleçleri (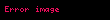


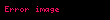


Görüldüğü gibi işlemleri sağdan sola doğru yapmanın geçerli bir nedeni vardır. Eğer soldan sağa doğru işlem yapsaydık, 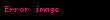

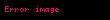
Değerler tabloları


| m\n | 1 | 2 | 3 | 4 | 5 | 6 | formül |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 16 | 32 | 64 |  |
| 2 | 2 | 4 | 16 | 65536 |  |  | 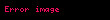 |
| 3 | 2 | 4 | 65536 |  |  | ||
| 4 | 2 | 4 |  |  |
Yukarıdaki tablo (Ackermann işlevi) ile hemen hemen aynıdır.


| m\n | 1 | 2 | 3 | 4 | 5 | formül |
|---|---|---|---|---|---|---|
| 1 | 3 | 9 | 27 | 81 | 243 |  |
| 2 | 3 | 27 | 7.625.597.484.987 |  |  | |
| 3 | 3 | 7.625.597.484.987 |  | 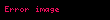 | ||
| 4 | 3 |  |  |
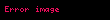

| m\n | 1 | 2 | 3 | 4 | 5 | formula |
|---|---|---|---|---|---|---|
| 1 | 10 | 100 | 1,000 | 10,000 | 100,000 |  |
| 2 | 10 | 10,000,000,000 |  |  | 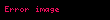 | 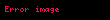 |
| 3 | 10 |  |  |  |  | |
| 4 | 10 |  |  |  |
2 ≤ n ≤ 9 için 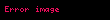
Hiperişlem dizisindeki sayısal sistemler
Knuth oklarından farklı olan Goodstein [1947] gösterim sisteminde hiperişlem dizisini kullandı. Bu gösterimde, negatif olmayan tam sayılar sistemini oluşturmak için 


- 0 ≤ n ≤ b-1 için, dijit yerine geçen n ile basitçe ifade edilebilir.
- n > b-1 için n ifade tekrarlanarak bulunabilir. Formdaki ilk n ifadesi;
dir.
- Burada xk, ..., x1, tahmini en büyük sayılardır.
- ...
.
- Daha sonra b-1'i aşan her xi, aynı şekilde ifade edilir ve böylece devam eder. Sadece 0, 1, ..., b-1 dijitleri içeren form sonuçlanana kadar bu işlem devam eder.
Bu bölümün kalan kısmında, hiperişlemleri ifade etmek için üstindislerin yerine 
Yüksel seviye işleçler kullanılarak gereksiz parantezlerden sakınılabilinir.
seviye-1 ifadeleri 
seviye-2 ifadeleri 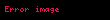
seviye-3 ifadeleri 
seviye-4 ifadeleri 
ve böylece devam eder.



Örnekler: 266 sayısının 1, 2, 3, 4 ve 5 seviyelerindeki eşsiz taban-2 ifadesi şöyledir:
.
Ayrıca bakınız
Alıntılar
- Knuth, Donald E., "Coping With Finiteness", Science vol. 194 n. 4271 (Aralık 1976), pp. 1235–1242.
- Eric W. Weisstein, Knuth yukarı ok gösterimi (MathWorld)
- Robert Munafo, Büyük Sayılar16 Mayıs 2017 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Knuth yukari ok gosterimi matematikte cok buyuk tam sayilarin gosterim yontemidir 1976 da Donald Knuth tarafindan gelistirildi Ackermann islevi ve ozel hiperislem serisi ile oldukca baglantilidir Carpmanin tekrarli hiperislem olarak tekrarli toplama ve us alma gibi gorulebilmesi fikrine dayanir Bu durumu devam ettirme tekrarli ussu tetrasyonu ve cogunlukla Knuth ok gosterimi kullanilarak ifade edilen asiri seri uretiminin geri kalanini meydana getirir TanitimDomino etkisi Tumevarim 3 boyutlu bilgisayar grafigi Toplama carpma us alma gibi siradan aritmetiksel islemler hiperislem serisinde dogal olarak soyle ifade edilir Bir dogal sayiyi carpma tekrarli toplama olarak soyle ifade edilebilir a b a a a b tane a displaystyle begin matrix a times b amp amp underbrace a a dots a amp amp b mbox tane a end matrix Ornegin 4 3 4 4 4 123 tane 4 displaystyle begin matrix 4 times 3 amp amp underbrace 4 4 4 amp amp 12 amp amp 3 mbox tane 4 end matrix b displaystyle b nin dogal kuvveti tekrarli carpma olarak ifade edilebilir ki Knuth onu tek bir yukari ok ile ifade etti a b ab a a a b tane a displaystyle begin matrix a uparrow b a b amp underbrace a times a times dots times a amp b mbox tane a end matrix Ornegin 4 3 43 4 4 4 643 tane 4 displaystyle begin matrix 4 uparrow 3 4 3 amp underbrace 4 times 4 times 4 amp amp 64 amp 3 mbox tane 4 end matrix Islemlerin serisini uslu gosterimden daha fazla genisleterek tekrarli usleri tetrasyonu ifade etmek icin Knuth bir cift ok operatoru tanimladi soyle ki a b ba aa a a a a b tane ab tane a displaystyle begin matrix a uparrow uparrow b amp b a amp underbrace a a a amp amp underbrace a uparrow a uparrow dots uparrow a amp amp b mbox tane a amp amp b mbox tane a end matrix Ornegin 4 3 34 444 4 4 4 4256 1 3 101543 tane 43 tane 4 displaystyle begin matrix 4 uparrow uparrow 3 amp 3 4 amp underbrace 4 4 4 amp amp underbrace 4 uparrow 4 uparrow 4 amp amp 4 256 approx 1 3 times 10 154 amp amp 3 mbox tane 4 amp amp 3 mbox tane 4 end matrix Burada ve asagidaki degerlendirmede Knuth ok isleclerini soldan saga dogru yerlestirme uslu sayilarda oldugu gibi islecleri birlestirme olarak tanimlanir Bu aciklamadan 3 2 33 27 displaystyle 3 uparrow uparrow 2 3 3 27 3 3 333 327 7 625 597 484 987 displaystyle 3 uparrow uparrow 3 3 3 3 3 27 7 625 597 484 987 3 4 3333 37625597484987 displaystyle 3 uparrow uparrow 4 3 3 3 3 3 7625597484987 3 5 33333 337625597484987 displaystyle 3 uparrow uparrow 5 3 3 3 3 3 3 3 7625597484987 etc Bu zaten epeyce buyuk bazi sayilari ifade eder Fakat Knuth bunu gosterimle notasyon yapti Simdi de iki ok islecli pentasyon olarak da bilinir tekrarli uygulamalar icin uc ok islecini taniyalim a b a a a b tane a displaystyle begin matrix a uparrow uparrow uparrow b amp underbrace a uparrow uparrow a uparrow uparrow dots uparrow uparrow a amp b mbox tane a end matrix ardindan dort ok isleci a b a a a b tane a displaystyle begin matrix a uparrow uparrow uparrow uparrow b amp underbrace a uparrow uparrow uparrow a uparrow uparrow uparrow dots uparrow uparrow uparrow a amp b mbox tane a end matrix ve boyle devam eder Genel kural bir n displaystyle n ok isleci n 1 displaystyle n 1 ok islec serisinin sagina dogru yayilarak gider Sembolik olarak a b a a a a a n n 1 n 1 n 1 b tane a displaystyle begin matrix a underbrace uparrow uparrow dots uparrow b a underbrace uparrow dots uparrow a underbrace uparrow dots uparrow a dots a underbrace uparrow dots uparrow a quad n qquad underbrace quad n 1 quad n 1 qquad quad n 1 qquad qquad quad b mbox tane a end matrix Ornekler 3 2 3 3 333 327 7 625 597 484 987 displaystyle 3 uparrow uparrow uparrow 2 3 uparrow uparrow 3 3 3 3 3 27 7 625 597 484 987 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 tane 3 3 3 3 7 625 597 484 987 tane 3 displaystyle begin matrix 3 uparrow uparrow uparrow 3 3 uparrow uparrow 3 uparrow uparrow 3 3 uparrow uparrow 3 uparrow 3 uparrow 3 amp underbrace 3 uparrow 3 uparrow dots uparrow 3 amp 3 uparrow 3 uparrow 3 mbox tane 3 end matrix begin matrix amp underbrace 3 uparrow 3 uparrow dots uparrow 3 amp mbox 7 625 597 484 987 tane 3 end matrix a nb displaystyle a uparrow n b gosterimi n tane ok kullanarak a b displaystyle a uparrow uparrow dots uparrow b seklinde ifade etmek yaygin bir sekilde kullanilir Gosterimab displaystyle a b gibi bir ifadede us olan b displaystyle b yi taban sayisi olan a displaystyle a nin ustindisi olarak yazmak ustel gosterim olarak bilinir Fakat programlama dilleri ve e posta gibi bircok ortam iki boyut duzeni desteklemez Bu tur ortamlar icin insanlar a b displaystyle a uparrow b seklinde lineer gosterim gelistirdi Yukari ok kuvvetin artisidir Eger karakter yukari ok icermezse onun yerine duzeltme isareti kullanilir ab displaystyle a b seklindeki ustindis gosterimi genellestirme icin kendini iyi ifade etmez Bundan dolayidir ki Knuth cizgisel gosterim olan a b displaystyle a uparrow b seklinde bir gosterim uretti Yukari ok gosterimini kuvvet terimleriyle yazma Bilinen uslu gosterimi kullanarak a b displaystyle a uparrow uparrow b yazmaya kalkismak uslu kule olusturur Ornegin a 4 a a a a aaaa displaystyle a uparrow uparrow 4 a uparrow a uparrow a uparrow a a a a a Eger b bir degisken veya cok buyuk sayi ise uslu kule su ornekte oldugu gibi noktalar kullanarak yazilir ve kulenin yuksekligi belirtilir a b aa a b displaystyle a uparrow uparrow b underbrace a a a b Bu gosterime devam edersek a b displaystyle a uparrow uparrow uparrow b ifadesi uslu kule yiginlari ile yazilabilir Her birinin aciklamasi bir digerinin uzerine yazilir a 4 a a a a aa a aa a aa a a displaystyle a uparrow uparrow uparrow 4 a uparrow uparrow a uparrow uparrow a uparrow uparrow a underbrace a a a underbrace a a a underbrace a a a a Tekrar eger b bir degisken veya cok buyuk sayi ise yigin nokta kullanilarak ve onun yuksekligini belirtilerek yazilir a b aa a aa a a b displaystyle a uparrow uparrow uparrow b left underbrace a a a underbrace a a a underbrace vdots a right b Daha da arttirirsak a b displaystyle a uparrow uparrow uparrow uparrow b ifadesi uslu kule yiginlarindan olusan birkac sutun olarak yazilir Her bir sutun yigindaki uslu kulenin sayisini aciklar a 3 a a a aa a aa a a aa a aa a a aa a aa a a a displaystyle a uparrow uparrow uparrow uparrow 3 a uparrow uparrow uparrow a uparrow uparrow uparrow a left left left underbrace a a a underbrace a a a underbrace vdots a right underbrace a a a underbrace a a a underbrace vdots a right underbrace a a a underbrace a a a underbrace vdots a right a Daha genel bir ifadeyle a b aa a aa a a aa a aa a a a b displaystyle a uparrow uparrow uparrow uparrow b underbrace left left left underbrace a a a underbrace a a a underbrace vdots a right underbrace a a a underbrace a a a underbrace vdots a right cdots right a b Bu a nb displaystyle a uparrow n b yi herhangi bir a n ve bnin tekrarli ussunun tekrarli ussu olarak ifade eder Tetrasyonu kullanma ba displaystyle b a seklindeki tetrasyon gosterimi bu diyagramlari daha basit yapmamizi saglarken diger yandan geometriksel ifadede calisabiliriz bu tetrasyon kuleleri olarak adlandirilir a b ba displaystyle a uparrow uparrow b b a a b a aa b displaystyle a uparrow uparrow uparrow b underbrace a a a b a b a aa a aa a b displaystyle a uparrow uparrow uparrow uparrow b left underbrace a a a underbrace a a a underbrace vdots a right b Son olarak dorduncu Ackermann sayisi 4 44 displaystyle 4 uparrow 4 4 soyle ifade edilebilir 4 44 4 44 4 44 4 4 44 4 44 4444 displaystyle underbrace 4 4 4 underbrace 4 4 4 underbrace 4 4 4 4 underbrace 4 4 4 underbrace 4 4 4 4 4 4 4 GenellestirmelerCok buyuk sayilarda Knuth yukari ok gosteriminin carpim oklari elverissiz kalir Bunun yerine n ok isleci olan n displaystyle uparrow n ve oklarin degisken sayisini aciklamak icin veya esdegeri olan hiperislemler kullanilir Bazi sayilar oyle buyuktur ki gosterimler bile onlari ifade etmekte aciz kalir Graham sayisini buna ornek gosterebiliriz Bunlar icin Conway dizisi ok gosterimi kullanilabilir Uc elemanli bir dizi diger gosterimlerle esdegerdir Fakat dort veya daha fazla elemanli diziler daha kuvvetlidir a nb hiper a n 2 b a b n Knuth islec Conway displaystyle begin matrix a uparrow n b amp amp mbox hiper a n 2 b amp amp a to b to n mbox Knuth amp amp mbox islec amp amp mbox Conway end matrix Kucuk sayilar icin Knuth ok gosterimi buyukleri icin de Conway dizisi veya hiperislemlerin kullanilmasi tavsiye edilir Aciklamaa b n displaystyle a b n tam sayi ve b 0 n 1 displaystyle b geq 0 n geq 1 olmasi sartiyla yukari ok gosterimi normalde soyle tanimlanir a nb ab eger n 1 1 eger b 0 a n 1 a n b 1 aksi takdirde displaystyle a uparrow n b left begin matrix a b amp mbox eger n 1 1 amp mbox eger b 0 a uparrow n 1 a uparrow n b 1 amp mbox aksi takdirde end matrix right Tum yukari ok islecleri a b displaystyle a uparrow b seklindeki normal ustel gosterim de dahil saga birlesmedir Ornegin iki veya daha fazla isleci iceren ifadede islem sagdan sola dogru yapilir Ornegin a b c a b c displaystyle a uparrow b uparrow c a uparrow b uparrow c a b c displaystyle neq a uparrow b uparrow c ornegin 3 3 333 displaystyle 3 uparrow uparrow 3 3 3 3 burada 3 33 327 7625597484987 displaystyle 3 3 3 3 27 7625597484987 iken diger tarafta 33 3 273 19683 displaystyle left 3 3 right 3 27 3 19683 Goruldugu gibi islemleri sagdan sola dogru yapmanin gecerli bir nedeni vardir Eger soldan saga dogru islem yapsaydik a b displaystyle a uparrow uparrow b soyle olurdu a a b 1 displaystyle a uparrow a uparrow b 1 Boylece displaystyle uparrow uparrow gerekli yeni bir islem olmazdi Degerler tablolari2 mn displaystyle 2 uparrow m n i hesaplama sonsuz bir tablodaki terimleri yeniden belirleyebiliriz 2n displaystyle 2 n sayilarini en ust satira koyduk 1 2 4 8 16 seklinde devam eden satir Tablodaki bir sayiyi tanimlamak icin tam solundaki sayiyi alin ardindan onceki satirdaki istenen sayiyi bulun Bulundugunuz yer size sayinin degerini verecektir 2 mn displaystyle 2 uparrow m n hiper asiri 2 m 2 n 2 n m degerleri m n 1 2 3 4 5 6 formul1 2 4 8 16 32 64 2n displaystyle 2 n 2 2 4 16 65536 265536 2 0 1019 729 displaystyle 2 65536 approx 2 0 times 10 19 729 2265536 106 0 1019 728 displaystyle 2 2 65536 approx 10 6 0 times 10 19 728 2 n displaystyle 2 uparrow uparrow n 3 2 4 65536 22 2 65536 tane 2 displaystyle begin matrix underbrace 2 2 2 65536 mbox tane 2 end matrix 2 n displaystyle 2 uparrow uparrow uparrow n 4 2 4 22 2 65536 tane 2 displaystyle begin matrix underbrace 2 2 2 65536 mbox tane 2 end matrix 2 n displaystyle 2 uparrow uparrow uparrow uparrow n Yukaridaki tablo Ackermann islevi ile hemen hemen aynidir 3 mn displaystyle 3 uparrow m n ni hesaplama 3n displaystyle 3 n sayilarini en ust satira koyduk ablodaki bir sayiyi tanimlamak icin tam solundaki sayiyi alin ardindan onceki satirdaki istenen sayiyi bulun Bulundugunuz yer size sayinin degerini verecektir 3 mn displaystyle 3 uparrow m n hiper 3 m 2 n 3 n m degerleri m n 1 2 3 4 5 formul1 3 9 27 81 243 3n displaystyle 3 n 2 3 27 7 625 597 484 987 37 625 597 484 987 displaystyle 3 7 625 597 484 987 3 n displaystyle 3 uparrow uparrow n 3 3 7 625 597 484 987 33 3 7 625 597 484 987 tane 3 displaystyle begin matrix underbrace 3 3 3 7 625 597 484 987 mbox tane 3 end matrix 3 n displaystyle 3 uparrow uparrow uparrow n 4 3 33 3 7 625 597 484 987 tane 3 displaystyle begin matrix underbrace 3 3 3 7 625 597 484 987 mbox tane 3 end matrix 3 n displaystyle 3 uparrow uparrow uparrow uparrow n 10 mn displaystyle 10 uparrow m n yi hesaplama 10n displaystyle 10 n sayilarini en ust satira koyduk Tablodaki bir sayiyi tanimlamak icin tam solundaki sayiyi alin ardindan onceki satirdaki istenen sayiyi bulun Bulundugunuz yer size sayinin degerini verecektir 10 mn displaystyle 10 uparrow m n hiper 10 m 2 n 10 n m degerleri m n 1 2 3 4 5 formula1 10 100 1 000 10 000 100 000 10n displaystyle 10 n 2 10 10 000 000 000 1010 000 000 000 displaystyle 10 10 000 000 000 101010 000 000 000 displaystyle 10 10 10 000 000 000 10101010 000 000 000 displaystyle 10 10 10 10 000 000 000 10 n displaystyle 10 uparrow uparrow n 3 10 1010 10 10 copies of 10 displaystyle begin matrix underbrace 10 10 10 10 mbox copies of 10 end matrix 1010 10 1010 copies of 10 displaystyle begin matrix underbrace 10 10 10 10 10 mbox copies of 10 end matrix 1010 10 101010 tane 10 displaystyle begin matrix underbrace 10 10 10 10 10 10 mbox tane 10 end matrix 10 n displaystyle 10 uparrow uparrow uparrow n 4 10 10 1010 10 copies of 10 displaystyle begin matrix underbrace 10 10 10 10 mbox copies of 10 end matrix 10 1010 1010 tane 10 displaystyle begin matrix underbrace 10 10 10 10 10 mbox tane 10 end matrix 10 n displaystyle 10 uparrow uparrow uparrow uparrow n 2 n 9 icin 10 mn displaystyle 10 uparrow m n sayilarinin sayisal sirasi m nin en belirgin sayi oldugu Boylece bu 8 sutunluk sayilar icin sayisal siralama basit satirdan satiradir 97 sutunluk sayilar icin ayni uygulama 3 n 99 dir ve ve eger m 1 den baslarsak 3 n 9 999 999 999 olurHiperislem dizisindeki sayisal sistemlerKnuth oklarindan farkli olan Goodstein 1947 gosterim sisteminde hiperislem dizisini kullandi Bu gosterimde negatif olmayan tam sayilar sistemini olusturmak icin displaystyle times uparrow uparrow uparrow dots kullandi 1 2 3 4 displaystyle quad 1 2 3 4 dots gibi ustindisleri displaystyle times uparrow uparrow uparrow dots gibi super isleclerle iliskilendirdi Bunu n tam sayisinin kesin kalitsal temsili olarak adlandirdi k seviyesi ve b tabani sadece k hiperislemleri ve sadece 0 1 b 1 dijitlerini kullanarak ifade edilebilir 0 n b 1 icin dijit yerine gecen n ile basitce ifade edilebilir n gt b 1 icin n ifade tekrarlanarak bulunabilir Formdaki ilk n ifadesi b k xk k 1 xk 1 k 2 x2 1 x1 displaystyle b k x k k 1 x k 1 k 2 dots x 2 1 x 1 dir Burada xk x1 tahmini en buyuk sayilardir b k xk n displaystyle b k x k leq n b k xk k 1 xk 1 n displaystyle b k x k k 1 x k 1 leq n b k xk k 1 xk 1 k 2 x2 1 x1 n displaystyle b k x k k 1 x k 1 k 2 dots x 2 1 x 1 leq n Daha sonra b 1 i asan her xi ayni sekilde ifade edilir ve boylece devam eder Sadece 0 1 b 1 dijitleri iceren form sonuclanana kadar bu islem devam eder Bu bolumun kalan kisminda hiperislemleri ifade etmek icin ustindislerin yerine displaystyle times uparrow uparrow uparrow uparrow uparrow uparrow dots gibi ifadeler kullanilacak Yuksel seviye islecler kullanilarak gereksiz parantezlerden sakinilabilinir seviye 1 ifadeleri b X displaystyle b X seklinde forma sahiptir seviye 2 ifadeleri b X Y displaystyle b times X Y seklinde forma sahiptir seviye 3 ifadeleri b X Y Z displaystyle b uparrow X times Y Z seklinde forma sahiptir seviye 4 ifadeleri b X Y Z T displaystyle b uparrow uparrow X uparrow Y times Z T seklinde forma sahiptir ve boylece devam eder 0 1 1 1 displaystyle 0 times 1 uparrow 1 uparrow uparrow 1 gibi ornekler cikartilarak ifadeler kisaltilabilir Ornegin 6 sayisinin seviye 3 taban 2 ifadesi 2 2 1 1 0 1 2 1 1 0 displaystyle 2 uparrow 2 uparrow 1 times 1 0 times 1 2 uparrow 1 times 1 0 dir Bunun kisaltilmis hali 2 2 2 displaystyle 2 uparrow 2 2 olur Ornekler 266 sayisinin 1 2 3 4 ve 5 seviyelerindeki essiz taban 2 ifadesi soyledir Seviye 1 266 2 2 2 133 2s ile displaystyle text Seviye 1 266 2 2 dots 2 text 133 2s ile Seviye 2 266 2 2 2 2 2 2 2 2 1 1 displaystyle text Seviye 2 266 2 times 2 times 2 times 2 times 2 times 2 times 2 times 2 1 1 Seviye 3 266 2 2 2 1 2 2 1 2 displaystyle text Seviye 3 266 2 uparrow 2 uparrow 2 1 2 uparrow 2 1 2 Seviye 4 266 2 2 1 2 2 2 2 2 displaystyle text Seviye 4 266 2 uparrow uparrow 2 1 uparrow 2 2 uparrow uparrow 2 times 2 2 Seviye 5 266 2 2 2 2 2 2 2 displaystyle text Seviye 5 266 2 uparrow uparrow uparrow 2 uparrow uparrow 2 2 uparrow uparrow uparrow 2 times 2 2 Ayrica bakinizHiperislem TetrasyonAlintilarKnuth Donald E Coping With Finiteness Science vol 194 n 4271 Aralik 1976 pp 1235 1242 Eric W Weisstein Knuth yukari ok gosterimi MathWorld Robert Munafo Buyuk Sayilar16 Mayis 2017 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State