Hayat Çizgisi

Fizikte, hayat çizgisi bir objenin 4 boyutlu uzayda işlediği yola denir. Objenin geçmiş mekanını her an takip etmeye de bu ad verilir. Hayat çizgisi yörüngeden ayrı bir kavramdır. Bu kavramlar zaman boyutuyla ayrılır. Ve genelde yörüngelerden daha geniş bir alanı temsil ederler, diğerlerine oranla özel göreliliğin gerçek doğasını ortaya çıkarırlar. Bu fikir Hermann Minkowski tarafından ortaya atılmıştır.Bu terim, genelde Görelilik Teorisinde kullanılır (özel görelilik ve genel görelilik).

Dünya çizgileri olayların oluşunu temsil ederler. Bu terimin kullanılması herhangi bir teoriyle bağlı olmamasına rağmen, çoğunlukla insanların zaman ve mekan bazında yaptıklarını temsil etmekte kullanılır. İnsanların geçmişini anlatır. Bir insanın doğumundan ölümüne kadar olan zamanı konu alabilir. Bir geminin günlüğü, geminin hayat çizgisi olarak tanımlanır. Bunun için günlükte zaman ve mekan etiketlerinin olması gerekmektedir. Geminin hayat çizgisi geminin hızını hesaplamakta ve Dünya üzerinde konumunu belirlemekte kullanılabilir.

Fizikte Kullanımı

Fizikte, hayat çizgileri herhangi bir objenin uzay-zaman içerisinde objenin geçmişini tanımlamak için kullanılır. Hayat çizgileri uzay zaman içinde özel bir eğridir. Zamansal bir uzay-zaman eğrisidir. Hayat çizgisinin her bir noktası zamansal ve uzaysal düzlemde o objenin verilen zamanda nerede olduğunu temsil eder.

Örnek vermek gerekirse, Dünya'nın yörüngesi neredeyse elipstir, üç boyutlu, kapalı uzayda bir eğridir. Dünya her yıl yörüngesel bazda aynı yere gelmektedir. Ancak hayat çizgisi açısından bakılacak olursa, aynı yere farklı bir zamanda varacağı için, asla aynı noktaya dönemeyecektir.

Uzay-zaman, olay denilen noktaların birleşiminden oluşur, birlikte olayların tanımlandığı bir koordinat sistemi oluştururlar. Her bir olay dört adet numarayla tanımlanır. Zaman koordinatı ve üç ayrı mekan koordinatı. Bu yüzden uzay-zaman dört boyutlu bir uzaydır. Uzay-zamanın matematikteki karşılığı manifold'dur. Bu konsept daha yüksek boyutlara da uygulanabilir. Dört boyutun görselleştirilebilmesi için en az iki koordinat gereklidir. Olaylar Minkowski Diyagramı ile tarif edilir. Uçaklar da bunu kullanır. Zaman koordinatlarıyla, yatay ve dikey koordinatlarını söylerler.

Hayat çizgisi uzay-zamanda tek bir noktayı takip eder. ise analog halde iki boyutlu bir yüzeyde tek boyut gibi (çizgi) uzay-zaman yolculuğunu ifade eder. Bir ucu açık çizgidir. (Işın gibi.) Sabit kısım ise kütledir. Bu açıdan dünya çizgileri olayları tanımlamak için bir araçtır.

Bir tek boyutlu eğri ya da çizgi tek fonksiyonlu koordinatla tanımlanabilir. Bu parametrelerin her biri bu çizgi üzerinde belli bir zamanda olan yerini temsil eder. Matematiksel manada eğri dört koordinat fonksiyonuyla tanımlanır fakat bir parametreye dayandırılır. Uzay zamanın grafiği dört koordinatın üçünün sabit ve sürekli olduğu fonksiyonlardır.

Bazen dünya çizgileri terimi uzay zamandaki tüm eğriler için kullanılır, bu da kafa karışıklığına yol açar. Daha net anlatmak gerekirse, dünya çizgileri bir parçacığın uzay zamandaki geçmişini takip etmeye denir. Bu gözlemi yapana gözlemci denir. Gözlemci belli bir zaman için parçacığı eğimde gözler, hayat çizgisi boyunca izler.

Uzay-Zaman Eğrilerinin Örnekleri

Üç farklı hayat çizgisi sabit hızla hareket etmektedir. T zamanı, x ise mesafeyi temsil etmektedir. Yatay çizgiden oluşan eğim, bir dal olabilir ve bu normal bir hayat çizgisi tanımına uymayabilir. Parametreler dalın uzunluğunu temsil eder. Uzay koordinatında sabit dikey bir çizgi dinlenen bir objeyi temsil edebilir. Eğilmiş bir çizgi sabit hızlı bir parçacığı gösteriyor olabilir. Çizginin dikey eğimi ne kadar fazlaysa, hız o kadar yüksektir.

İki bağımsız çizginin buluşmasına “kesişme” denir. İki objenin kesişik başlayıp ayrılması, parçacıkların birleşmesi, çarpışması ya da birinin diğerini yutması anlamına gelebilir.

Hayat Çizgisinin Tanjant Vektörü

Hayat çizgisini tanımlayan dört koordinat reel fonksiyonlardır ve kalkülüste değiştirilerek kullanılabilir. Metrik sistemin olmadığı bir yerde, parametredeki değerin eğim noktasındaki farklılığından bahsedilebilir. Limitte, bu farklılık bir vektörü ifade eder. Bu vektör, bir noktanın hayat çizgisinin tanjant vektörüdür. Bu üç boyutlu objenin hızıyla ilişkilendirilmiştir. Bu bir dört boyutlu vektördür, noktayla tanımlanır.

Özel Görelilikte Hayat Çizgileri

Şu ana kadar hayat çizgisi olayların arası ilişkilendirilmeden anlatıldı. Fakat özel görelilik olası dünya çizgilerine bazı sınırlamalar koyar. Özel görelilik uzay zamanın tanımına bazı sınırlamalar getirir. Bunlar hızlanmayan özel koordinat sistemleri ile incelenir. Bunlara eylemsiz koordinat sistemleri denir. Böyle sistemlerde, ışığın hızı sabittir. Uzay zamanın yapısı belirlenir. Bu da tüm olaylar için gerçek bir sayı verir. Bu bazen uzay zaman metriği olarak tanımlanır, ama bazen ayrı olaylarda sonuç sıfır çıkar.

Sabit hızlı obje ve parçacıkların dünya çizgilerine adı verilir. Minkowski uzayında bunlar düz çizgilerdir. Çoğunlukla zaman birimleri ışığın hızının sabit olduğu çizgilerle temsil edilir. Bunlar çoğunlukla 45 derecelik sabit açılıdırlar ve zaman ekseninde bir koni oluştururlar.

Genelde uzay zamanda kullanışlı olan üç eğri vardır; -Işık benzeri eğriler: Her noktada ışık hızındadırlar. Uzay zamanda koni oluştururlar. Bunlar uzay zamanı ikiye böler. Koni uzay zamanda iki boyutludur, çizimlerde iki boyutlu görünür. Işık konisine örnek vermek gerekirse, üç boyutlu yüzeyde tüm olası ışınların uzay zamanda vardığı ve ayrıldığı ortak nokta düşünülebilir. Burada bir boyut yok sayılmıştır. -Zaman benzeri eğriler: Işık hızından az bir hıza sahip olan objelerindir bu eğimler ışık benzeri konilere düşerler. Yukarıdaki tanım gibi, dünya çizgileri uzay zamanda zaman benzeri eğrilerdir. -Uzay benzeri eğriler: Işık konisinin dışına düşer. Bu tarz eğriler, bir nesnenin uzunluğunu tarif edebilirler. Silindirin çevresi ve bir dalın uzunluğu uzay benzeri eğrilerdir.

Hayat çizgisinde olan bir olay, uzay zamanı üç parçaya ayırır (Minkowski uzayı). -Olayın geleceği, zaman benzeri eğrilerin gelecek ışık konisi içinde duranları tarafından gerçekleştirilir. -Olayın geçmişi, olayı etkileyebilecek/etkilemiş olaylardır (Geçmişte dünya çizgileri kesişmiş olabilir). -Olayın ışık konisi, olayla kesişen ışınların olayla kesiştiği noktalardır. Geceleri gökyüzüne baktığımızda tüm uzay zamanın geçmiş konisini görebilmemiz gibi.

İki ışık konisinin arasında kalan alan başka her yerdir. Gözlemci için bu yerler ulaşılmazdır. Sadece geçmişi gözlemciye geçmişten etki edebilir. Bu, Güneşe baktığımızda sekiz dakika öncesini görmemiz gibidir. Bize "şu an", Güneşe sekiz dakika öncesidir. Galileo'cu ve Newton'cu teorilerin aksine, diğer yerler kalındır ve dört boyutlu uzay zamandır. Şimdi, genelde uzay zamanda tek bir olaydır.

Simultane Hiperdüzlem

Hayat çizgisi ${\displaystyle \scriptstyle w(\tau )\in R^{4}}$ 4 boyutlu ${\displaystyle \scriptstyle v={\frac {dw}{d\tau }}}$ zaman benzeri bir vektörü temsil ettiğinden, Minkowski formu ${\displaystyle \scriptstyle \eta (v,x)}$ bu ${\displaystyle \scriptstyle R^{4}\rightarrow R}$ by ${\displaystyle \scriptstyle x\mapsto \eta (v,x).}$ boş olan uzay kısmını belirler. "N" bu boş uzayı temsil eder.

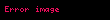
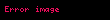
Bu boş uzaya da denir. Bu düzlemin göreleliği N'ye ya da V'ye göre değişir. Hatta N ortogonaldir. İki hayat çizgisi alakalı olduğunda bunlar aynı simultane hiperdüzlemi paylaşır. Bu hiperdüzlem matematiksel olarak var olsa da, fiziksel manada, ışığın hareketine bağlıdır. Örnek olarak Coulomb'un elektrostatik gücü simultane hiperdüzlem aracılığıyla resmedilebilir, ama güç ve yükün göreli ilişkileri aptalca sonuçlara yol açabilir.

Genel Görelilikte Hayat Çizgileri

Kullanımı özel görelilikle aynıdır. Ayrıldığı nokta ise . Bir metriğin var olması Einstein'ın alan denklemleri tarafından belirlenir ve uzay zamanın kütle enerji dağılımına bağlıdır. Metriklerin ışık benzeri (boş), uzay benzeri ve zaman benzeri eğrileri vardır. Ayrıca genel görelilikte dünya çizgileri genellikle uzay zamanda zaman benzeri eğrilerdir. Buna rağmen ışık konisinin açısı 45 derece olmayabilir. Serbest düşüşteki objeler ya da parçacıkların dünya çizgilerine (Güneş etrafındaki gezegenler ya da uzaydaki astronot) jeodezik denir.

Edebiyatta Hayat Çizgileri

1884'te "Dördüncü Boyut Nedir?" adlı bir makale yazdı ve bunu romantik bilimsel bir hikâye olarak yayımladı. Hinton der ki; "Neden dördüncü boyutlu benliklerimiz, üçüncü boyuttaki benliklerimizin bilinçleriyle birleşmiyor olmasın?"

İnsani dünya çizgilerinin genel tanımı Toronto Üniversitesi'nden tarafından yapıldı. "Bir Cumartesi günü verilen bir dersi hatırlıyorum. Adı matematiksel fantezi idi ve öyleydi de! Her insanın doğumundan ölümüne uzanan, ruhsal bir aura ile bağlı olduğu bir yoldan bahsedildi. Gençlikte kurulan küçük bağlardan, hayatın ilerisinde kurulan sıkı bağlara kadar her şey anlatıldı."

Hayat çizgilerini basitleştirdikleri için, ki bu dört boyutu üç boyuta indirgemek oluyor, zaman yolculuğu içeren yazılmış tüm bilimkurgu hikâyeleri maalesef hayalden ibarettir. Normalde zaman makinaları ya da süper yetenekli bir insan zamanda sıçramalar yapar. O sıçrama sonrası hiçbir şey değişmez ama gerçekte bu gerçekleşebilseydi Güneş Sistemi hatta tüm galaksi varılan noktada bambaşka bir yerde olacaktı. Bu yüzden zamanda sıçrama yapılabilmesi için, ayrıca ışınlanmak da gereklidir. Gidilecek yerin 3 boyutlu konumu, lineer ve açısal momentumu da lazımdır.

Hayat Çizgileri, J'ın adlı çizgiromanında uzayda sihirli maceralar adlı hikâyede geçer. Bu hikâyede Patates Topates ve Şerif Pony yanlışlıkla dünyayı astroitlerle çarpışmaktan kurtaran bir hayat çizgisini siler. Hikâyeye göre, spesifik bir hayat çizgisini hesaplamak "utanç verici düzeyde" kolaydır ve silmek için yapılması gereken tek şey bir arama yapıp koordinatları girmek, ardından 3'e basmaktır.

Bir kısa hikâyesinde yazar Robert Heinlein bir insanın hayat çizgisini şöyle anlatır; -Gazetecilerden birine yaklaştı: "Hadi seni örnek alalım. Adın Rogers değil mi? Çok iyi Rogers sen 4 yönde gerçekleşen bir uzay zaman olayısın. 1.80m boy, 60cm en, zaman boyutun ve genişliğin bir hediye kadar. Bir çizgisin, bir ucunda süt emen bir bebek, bir ucunda seksenlik bir moruk! Bu uzay zaman olayını şöyle düşün. Uzun pembe bir solucan var, adı Rogers. Yıllar geçiyor ve o solucanın bir kısmı mezarda, bir kısmı ise henüz doğmamış!"

Kaynakça

1. ^ George Gamow (1970) My World Line: An Informal Autobiography, ,
2. ^ (1884) What is the fourth dimension, Scientific Romances, link from Internet Archive
3. ^ (1979) The Mathematics Department in the University of Toronto, p. 19, University of Toronto Press
4. ^ Day 6 (The Multiverse, The Pool, and Elves). . 28 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Ocak 2016.