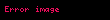| × | 1 | j |
|---|---|---|
| 1 | 1 | j |
| j | j | 1 |
Gerçel sayılarda olmayan ve karesi 1 olan bir sayının kümeye katılmasıyla kümeye hiperbolik sayılar kümesi denir. Tıpkı karmaşık sayılarda olduğu gibi, hiperbolik sayılar şeklinde yazılabilen sayılardır, ancak karmaşık sayılardan tek farkı denilen sayının

olarak tanımlanmasıdır. Bu sayılar fizikte, özellikle Özel görelilikte sıkça kullanılmaktadır. Daha anlaşılır bir tanımını şöyle yapabiliriz.
- olduğuna göre,
- neden olmasın varsayımı ile açıklayabiliriz.
Buradan geriye dönük tüm tanımlanan sayıların aslında bir varsayımdan ibaret olabileceği çıkarımını yapabiliriz. Yani alınan matematiksel modele göre çözümler üretiyoruz. Eğer h gibi bir sayı varsa bu fiziksel bir olayı açıklamak içindir. Buradan şu anlaşılır fiziksel olayları açıklamak için matematiğe ihtiyaç vardır veya fizik matematiğin görüntülerinden ibarettir. Buradan doğadaki olayların hepsinin matematikten ibaret olduğunu anlarız. Matematik soyuttur ama fizik gibi somut bir yansıması vardır. Eğer matematik bir fiziksel olayı açıklayamıyorsa bu olay fiziksel değildir.
Resmî tanım

polinomunun kökleri 1 ve -1 iken, bunların dışında başka bir 
bölüm halkasına hiperbolik sayılar kümesi denir ve genelde 
Böyle bir sayının polinom halkasının katsayılar kümesi olan gerçel sayılar kümesi 
Tanım
Bir bölünmüş-karmaşık sayı gerçek sayıların sıralı bir çifti formunda burada x ve y gerçek sayılar ve j niceli uygundur
seçilirse karmaşık sayı içindeki sonuçlardır. Bu sıradan karmaşık olanlardan bölünmüş karmaşık sayılar ayıran bu işareti değişimdir. Miktar j burada bir gerçek sayı değildir ancak bağımsız bir miktardır, bu ± 1'e eşit değildir.
Tüm bu z koleksiyonuna bölünmüş-karmaşık düzlem denir. Bölünmüş karmaşık sayıların Toplama ve çarpması aşağıdaki ile tanımlanır.
- (x + j y) + (u + j v) = (x + u) + j(y + v)
- (x + j y)(u + j v) = (xu + yv) + j(xv + yu).
Bu çarpma toplama üzerinde , ve .
Eşlenik, modül ve çift doğrusal form
Sadece karmaşık sayılar için, bölünmüş karmaşık eşlenik kavramını tanımlayabilirsiniz. Eğer
- z = x + j y
znin eşleniği olarak tanımlanır
- z∗ = x − j y.
Eşlenik olağan kompleks eşleniği ile benzer özelliklere taşır. Yani,
- (z + w)∗ = z∗ + w∗
- (zw)∗ = z∗w∗
- (z∗)∗ = z.
Bu üç özellik bölünmüş karmaşık eşleniğe işaret etmektedir 2.nin bir 'sıdır
Bir bölünmüş karmaşık sayının z = x + j y tarafından verilen modülü
önemli bir özelliği vardır, bu bölünmüş karmaşık çarpma tarafından korunmaktadır :
Bununla beraber, bu karesel form değildir ama oldukça yerine geçecek bir 'sıdır (1, −1), bu modül bir değildir.
Birleşimli ile verilir:
- 〈z, w〉 = Re(zw∗) = Re(z∗w) = xu − yv,
burada z = x + j y ve w = u + j v. modül için bir başka ifade ise
Pozitif-tanım olmadığından, bu çiftdoğrusal form bir değildir; yine de çift doğrusal form sık sık bir belirsiz iç çarpım olarak adlandırılır. Dil kötüye benzer bir norm olarak modül ifade eder. Bölünmüş-karmaşık sayının tersi olan ancak ve ancak onun modül sıfırda farklı (
Split-karmaşık sayılar boş elemanların tersi değildir. Burada bütün (a ± j a) formunun bazı a gerçek sayıları içindir.
Köşegen taban
Burada iki önemsiz olmayan ile verilen e = (1 − j)/2 ve e∗ = (1 + j)/2. Bu idempotent demektir hatırlayın ee = e ve e∗e∗ = e∗. Bu öğelerin her ikisi de null(boş):
Sıklıkla kullanmak için e ve e∗ ye bir alternatif olarak bölünmüş karmaşık düzlemde . Bu taban köşegen taban veya null taban olarak adlandırılır,bölünmüş-karmaşık sayı z taban içinde aşağıdaki gibi yazılabilir.
- z = x + j y = (x − y)e + (x + y)e∗.
Eğer z = ae + be∗ sayısını göstermek istiyorsak gerçek sayılar a ve b ile (a, b), ise bölünmüş-karmaşık çarpma ile verilir
- (a1, b1)(a2, b2) = (a1a2, b1b2).
Bu baz olarak, toplama ve çarpma ile tanımlanan ikili R ⊕ R direkt toplamı 'ya bölünmüş karmaşık sayılar için açıkça uyar.
köşegen bazında bölünmüş kompleks eşleniği aşağıdaki ile verilir
- (a, b)∗ = (b, a)
ve modülü aşağıdaki ile
aynı eşbiçimsel sınıfta uzanan olsa da içinde yerleşmiş kendi içinde farklı iki çizginin doğrudan toplamıdır. Bir düzlemsel haritalama olarak eşbiçimsel,,45 ° bir saat yönünün tersine bir √2 ile dönme oluşur ve ile bağlantı bölgesinin içinde özellikle bazen karışıklığa neden olmuştur . gerçekten, 



Geometri

eşlenik hiperbol ile ||z||=−1 (yeşil),
ve asimtotları ||z||=0 (kırmızı)
Minkowski iç çarpımı ile iki boyutlu gerçek vektör uzayı denen sıklıkla (1 + 1)-boyutlu ifade edilen Minkowski uzayıdır, R1,1 Öklid düzlemi R2geometrisi gibi çok karmaşık numaraları ile tarif edilebilir, Minkowski'nin düzlemi,R1,1 geometrisi bölünmüş kompleks numaraları ile tarif edilebilir. Noktaların kümesidir
R içindeki a her sıfırdan farklı bir hiperbol bir sağ ve sol dalı (a, 0) ve (−a, 0) den geçerek oluşur. Durum a = 1 birim hiperbol denir. Eşlenik hiperbol ile verilir
Noktaları seti ile bir üst ve alt geçen dalı (0, a) ve (0, −a). Hiperbol ve eşlenik hiperbol boş elemanlarının kümesini oluşturan iki köşegen asimptot'lara ayrılır
Bu iki hat (bazen boş koni olarak adlandırılır)R2 içinde dik olan ve eğimli ± 1 var. bölünmüş-karmaşık sayılar z ve w ise hiperbolik-dik olduğu söylenmektedir z, w = 0 dır. Sıradan diklik benzer olsa da, sıradan bir karmaşık sayı aritmetik ile bilinen özellikle de, bu durum daha güç algılanır. Bu uzay içinde aynı anda kavramının temelini oluşturur. Bölünmüş karmaşık sayılar için Euler formülü analogu olan
Bu için varken sadece çift güçler olduğu gerçeğini kullanarak bir güç seri açılımı elde edilebilir için tüm gerçek değerleri için θ bölünmüş karmaşık sayıλ = exp(jθ) norm 1'e sahiptir ve birim hiperbol sağ kolu yatıyor. Bu λ gibi Numaraları 'ler. olarak adlandırılabilir. λ tarafından çarpılan geometrik yapı korunur,.
Λ katsayısı 1, sahip olduğu herhangi bir λ ile herhangi bir bölünmüş karmaşık sayı z çarparak z ve modülü korunur ve bir hiperbolik dönme alarak, geometrik yapısını korur, kendilerini ve kendisi için boş koni hiperbolas alarak (bir veya bir gibi adlandırılır). Modülü (veya eşdeğer, iç çarpım) O(1, 1) adlı bir grup oluşturan korumak bölünmüş karmaşık düzlemde tüm dönüşümlerin kümesi SO+(1, 1) formu tarafından verilen dört ile birlikte bu grup hiperbolik dönme oluşturur
ve
Üstel harita
exp(jθ) tarafından θ ya gönderilen bir ile kullanılan üstel formül uygulaması:
Eğer bir çift-karmaşık sayı z köşegenin bir yatık şekli değil, ise z bir 'dır.
Matris gösterimleri
Bölünmüş-karmaşık sayılar
- z = x + j y
'i tarafından kolayca gösterilebilir
bölünmüş-karmaşık sayıların toplama ve çarpımı toplama ve çarpım matrisleri tarafından verilebilir.znin modülü mukabil matrisin determinantı tarafından verilir. Bu gösterim içinde,iki yüz olarak bölünmüş-karmaşık eşlenik matris tarafından çarparak karşılık gelir
herhangi bir gerçek sayı a, bir tarafından hiperbolik rotasyon a çarpımına karşılık gelen matris ile

Bölünmüş karmaşık sayı düzlemi diagonal bazında 
Şimdi ikinci dereceden formu 
böylece iki hiperboller Sile karşıkarşıya getirilir. 
Burada 'in konusunu bu bağlamda unutmayın Aslında bölünmüş kompleks sayıların farklı temsillerinin büyük bir sayıdadır. bölünmüş karmaşık sayının matris gösterimini yukarıdaki köşegen gösterim temsil etmektedir. Bölünmüş-karmaşık sayılar aşağıdaki matris gösterimi için z = (x, y) tarafından verilir:
Bu Jordan kurallı formu ile verilen:
burada 
Tarihçe
Bölünmüş karmaşık sayılar kullanılması 1848 uzanır 'yı ortaya çıkardı. spinlerin toplamını gösteren temsil bölünmüş karmaşık sayılar kullanır . Clifford şimdi adı verilen bir kuaterniyon cebir katsayıları olarak bölünmüş-karmaşık sayılar kullanımı tanıttı . O ögelere "motorlar" dendi,'tan alınan sıradan bir karmaşık sayının "rotor" eylemine paralel bir terimle çağrıldı. Benzerlik sıradan bir fonksiyonlar için bir kontrast fonksiyonlarına uzatılabilir . Yirminci yüzyıldan beri,bölünmüş-karmaşık çarpma yaygın bir uzayzaman - planının bir 'a destek olarak görülmüştür . Bu modelde, sayı z = x + y j içindeki y nanosaniye içindeki x burada ve y ölçülür bir uzay-zamansal planda, bir olay temsil eder. Gelecekteki olayların kadrandaki karşılığı {z : İfade hatası: Tanınmayan "'" noktalama karakteri.<x}, bölünmüş karmaşık polar ayrışma sahip olduğu 
birim hiperbol üzerinde çarpım ifadesi doğrudaş hızları için hızların toplanırlığını göstermektedir . Olayların eşzamanlılık hız a 'ya bağlıdır ;
a hızlı referans çerçevesinde orijin eşzamanlı olayların hattıdır. Iki olay z ve w olduğunda z∗w + zw∗ = 0. Kanonik olaylar exp(aj) vej exp(aj) orijini ile eşzamanlı olayları j exp(aj) ile orantılı olduğu referans çerçevesinin eksende dik hiperbolik ve Lie'dir . 1.935 J.C. Vignaux ve A.Durañona y Vedia Contribución bir las Ciencias Físicas y Matemáticas, , República Argentina (in Spanish) dört makalelerde bölünmüş Geometrik cebir ve fonksiyonlar teorisi geliştirdi. Bu açıklayıcı ve pedagojik denemeleri geniş takdir için konu sundu.
1941 yılında EF Allen zz∗ = 1 içinde yazılı bir üçgenin dokuz-nokta bir hiperbol kurmak için bölünmüş Geometrik aritmetik kullanılır .
1956 yılında Mieczyslaw Warmus Bulletin de l’Academie Polanaise des Sciences te "Yaklaşıklıklar Hesabı" (Referanslar bağlantıya bakınız) yayınladı. O bölünmüş karmaşık sayı ile bir [a, A] tespit
ve bir "yaklaşık sayı" olarak nitelendirdi. Matematiksel Yorumlar Mathematical Reviews..
1961 yılında Warmus aralığının orta noktası ve yarıçapı ifade olarak yaklaşık sayıda bileşenleri atıfta bulunarak, onun fuar devam etti.
Eşanlamlılar
Farklı otörler çift-kompleks sayılar için isimlerin büyük bir çeşitliliğini kullandı. Bunlardan bazıları şunlardır:
- (gerçek) tessarines, James Cockle (1848)
- (cebrik) motorlar, W.K. Clifford (1882)
- hiperbolik kompleks sayılar, J.C. Vignaux (1935)
- çiftgerçek sayılar, U. Bencivenga (1946)
- yaklaşık sayılar, Warmus (1956), for use in
- countercomplex veya hyperbolic numbers from
- ikikat sayılar, (1968) and (1990)
- anormal-kompleks sayılar, W. Benz (1973)
- kafakarıştırıcı sayılar, P. Fjelstad (1986) and Poodiack & LeClair (2009)
- Lorentz sayıları, F.R. Harvey (1990)
- hiperbolik sayılar, G. Sobczyk (1995)
- yarı-karmaşık sayılar, F. Antonuccio (1994)
- bölünmüş-karmaşık sayılar, B. Rosenfeld (1997)
- uzayzaman sayıları, N. Borota (2000)
- ikizkarmaşık sayılar, S. Olariu (2002)
Bölünmüş-karmaşık sayılar ve yüksek-boyutlu ilişkiler ('ler / eşdördeyler ve ) zaman zaman "Musean Sayılar" olarak adlandırılmıştır, öyle ki 'in geliştirdiği 'ın bir alt kümesidir.
Ayrıca bakınız
Bir modifiye ile elde edilen bölünmüş karmaşık sayılar daha yüksek mertebeden türevler, :
- (veya eş-dördey)
Lie Teorik olarak, daha soyut bir genelleme oluşur:
Cebir ve sayılar programları zarfı:
Kaynaklar ve Dış bağlantılar
- Francesco Antonuccio (1994) Semi-complex analysis and mathematical physics22 Ağustos 2016 tarihinde Wayback Machine sitesinde .
- Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica della algebra doppie dotate di modulo", Atti della real academie della scienze e belle-lettre di Napoli, Ser (3) v.2 No7. MR0021123.
- Benz, W. (1973)Vorlesungen uber Geometrie der Algebren, Springer
- N. A. Borota, E. Flores, and T. J. Osler (2000) "Spacetime numbers the easy way", 34: 159-168.
- N. A. Borota and T. J. Osler (2002) "Functions of a spacetime variable", Mathematics and Computer Education 36: 231-239.
- K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions, and sedenions", Appl. Math. Comput. 28:47–72.
- K. Carmody, (1997) "Circular and hyperbolic quaternions, octonions, and sedenions – further results", Appl. Math. Comput. 84:27–48.
- F. Catoni, D. Boccaletti, R. Cannata, V. Catoni, E. Nichelatti, P. Zampetti. (2008) The Mathematics of Minkowski Space-Time, , Basel. Chapter 4: Trigonometry in the Minkowski plane. .
- Cockle, James (1848) "A New Imaginary in Algebra", London-Edinburgh-Dublin Philosophical Magazine (3) 33:435–9.
- Clifford, W.K.,Mathematical Works (1882) edited by A.W.Tucker,pp. 392,"Further Notes on "
- De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
- Fjelstadt, P. (1986) "Extending Special Relativity with Perplex Numbers", American Journal of Physics 54:416.
- F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. . Contains a description of normed algebras in indefinite signature, including the Lorentz numbers.
- Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics, Soviet/AMS/Kluwer, Dordrect.
- (1985) "Transformations in Special Relativity", International Journal of Theoretical Physics 24:223–36.
- C. Musès, "Applied hypernumbers: Computational concepts", Appl. Math. Comput. 3 (1977) 211–226.
- C. Musès, "Hypernumbers II—Further concepts and computational applications", Appl. Math. Comput. 4 (1978) 45–66.
- Olariu, Silviu (2002) Complex Numbers in N Dimensions, Chapter 1: Hyperbolic Complex Numbers in Two Dimensions, pages 1–16, North-Holland Mathematics Studies #190, Elsevier .
- Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", 40(5):322–35.
- Rosenfeld, B. (1997) Geometry of Lie Groups Kluwer Academic Pub.
- Sobczyk, G.(1995) Hyperbolic Number Plane13 Kasım 2013 tarihinde Wayback Machine sitesinde ., also published in 26:268–80.
- Vignaux, J.(1935) "Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel", Contribucion al Estudio de las Ciencias Fisicas y Matematicas, Universidad Nacional de la Plata, Republica Argentina.
- M. Warmus (1956) "Calculus of Approximations"9 Mart 2012 tarihinde Wayback Machine sitesinde ., Bulletin de l'Academie Polonaise de Sciences, Vol. 4, No. 5, pp. 253–257;
- Yaglom, I. (1968) Complex Numbers in Geometry, translated by E. Primrose from 1963 Russian original, Academic Press, N.Y., pp. 18–20.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
bolunmus karmasik carpim 1 j1 1 jj j 1 Gercel sayilarda olmayan ve karesi 1 olan bir sayinin kumeye katilmasiyla kumeye hiperbolik sayilar kumesi denir Tipki karmasik sayilarda oldugu gibi hiperbolik sayilar a hb displaystyle a mathbf h b seklinde yazilabilen sayilardir ancak karmasik sayilardan tek farki denilen sayininBir modulu sifir kirmizi bir mavi ile altkumelerini gosteren bolunmus karmasik sayi duzleminin bir kismi ve bir eksigi olan yesil h2 1 displaystyle mathbf h 2 1 olarak tanimlanmasidir Bu sayilar fizikte ozellikle Ozel gorelilikte sikca kullanilmaktadir Daha anlasilir bir tanimini soyle yapabiliriz j2 1 displaystyle j 2 1 olduguna gore j2 1 displaystyle j 2 1 neden olmasin varsayimi ile aciklayabiliriz Buradan geriye donuk tum tanimlanan sayilarin aslinda bir varsayimdan ibaret olabilecegi cikarimini yapabiliriz Yani alinan matematiksel modele gore cozumler uretiyoruz Eger h gibi bir sayi varsa bu fiziksel bir olayi aciklamak icindir Buradan su anlasilir fiziksel olaylari aciklamak icin matematige ihtiyac vardir veya fizik matematigin goruntulerinden ibarettir Buradan dogadaki olaylarin hepsinin matematikten ibaret oldugunu anlariz Matematik soyuttur ama fizik gibi somut bir yansimasi vardir Eger matematik bir fiziksel olayi aciklayamiyorsa bu olay fiziksel degildir Resmi tanimR X displaystyle mathbb R X X2 1 displaystyle X 2 1 polinomunun kokleri 1 ve 1 iken bunlarin disinda baska bir h displaystyle mathbf h sayisinin da bu polinomun bir koku oldugunun varsayilmasiyla olusan R X X2 1 displaystyle mathbb R X X 2 1 bolum halkasina hiperbolik sayilar kumesi denir ve genelde H displaystyle mathbb H ya da H ile gosterilir Boyle bir sayinin polinom halkasinin katsayilar kumesi olan gercel sayilar kumesi R displaystyle mathbb R de de olmadigi gorulebilir ya da bu sayi yine 1 ya da 1 sayilardan birine esit olmak zorunda kalir Boylece bu sayi kumesi cebirin temel teoremi geregi bir cisim olamaz degismeli bir halka olur TanimBir bolunmus karmasik sayi gercek sayilarin sirali bir cifti formunda burada x ve y gercek sayilar ve j niceli uygundur ȷ2 1 displaystyle jmath 2 1 ȷ2 1 displaystyle jmath 2 1 secilirse karmasik sayi icindeki sonuclardir Bu siradan karmasik olanlardan bolunmus karmasik sayilar ayiran bu isareti degisimdir Miktar j burada bir gercek sayi degildir ancak bagimsiz bir miktardir bu 1 e esit degildir Tum bu z koleksiyonuna bolunmus karmasik duzlem denir Bolunmus karmasik sayilarin Toplama ve carpmasi asagidaki ile tanimlanir x j y u j v x u j y v x j y u j v xu yv j xv yu Bu carpma toplama uzerinde ve Eslenik modul ve cift dogrusal form Sadece karmasik sayilar icin bolunmus karmasik eslenik kavramini tanimlayabilirsiniz Eger z x j y znin eslenigi olarak tanimlanir z x j y Eslenik olagan kompleks eslenigi ile benzer ozelliklere tasir Yani z w z w zw z w z z Bu uc ozellik bolunmus karmasik eslenige isaret etmektedir 2 nin bir sidir Bir bolunmus karmasik sayinin z x j y tarafindan verilen modulu z zz z z x2 y2 displaystyle lVert z rVert zz z z x 2 y 2 onemli bir ozelligi vardir bu bolunmus karmasik carpma tarafindan korunmaktadir zw z w displaystyle lVert zw rVert lVert z rVert lVert w rVert Bununla beraber bu karesel form degildir ama oldukca yerine gececek bir sidir 1 1 bu modul bir degildir Birlesimli ile verilir z w Re zw Re z w xu yv burada z x j y ve w u j v modul icin bir baska ifade ise z z z displaystyle lVert z rVert langle z z rangle Pozitif tanim olmadigindan bu ciftdogrusal form bir degildir yine de cift dogrusal form sik sik birbelirsiz ic carpim olarak adlandirilir Dil kotuye benzer bir norm olarak modul ifade eder Bolunmus karmasik sayinin tersi olan ancak ve ancak onun modul sifirda farkli z 0 displaystyle lVert z rVert neq 0 Bir ogenin asagidaki ile verilir z 1 z z displaystyle z 1 z lVert z rVert Split karmasik sayilar bos elemanlarin tersi degildir Burada butun a j a formunun bazi a gercek sayilari icindir Kosegen taban Burada iki onemsiz olmayan ile verilen e 1 j 2 ve e 1 j 2 Bu idempotent demektir hatirlayin ee e ve e e e Bu ogelerin her ikisi de null bos e e e e 0 displaystyle lVert e rVert lVert e rVert e e 0 Siklikla kullanmak icin e ve e ye bir alternatif olarak bolunmus karmasik duzlemde Bu taban kosegen taban veya null taban olarak adlandirilir bolunmus karmasik sayi z taban icinde asagidaki gibi yazilabilir z x j y x y e x y e Eger z ae be sayisini gostermek istiyorsak gercek sayilar a ve b ile a b ise bolunmus karmasik carpma ile verilir a1 b1 a2 b2 a1a2 b1b2 Bu baz olarak toplama ve carpma ile tanimlanan ikili R R direkt toplami ya bolunmus karmasik sayilar icin acikca uyar kosegen bazinda bolunmus kompleks eslenigi asagidaki ile verilir a b b a ve modulu asagidaki ile a b ab displaystyle lVert a b rVert ab ayni esbicimsel sinifta uzanan olsa da icinde yerlesmis kendi icinde farkli iki cizginin dogrudan toplamidir Bir duzlemsel haritalama olarak esbicimsel 45 bir saat yonunun tersine bir 2 ile donme olusur ve ile baglanti bolgesinin icinde ozellikle bazen karisikliga neden olmustur gercekten R R displaystyle R oplus R icindeki sektorlerin bolge ye karsilik gelen duzlemi ile bu birim cember asagida verilmistir a b R R ab 1 displaystyle lbrace a b in R oplus R ab 1 rbrace birim cember anlasilir cosh a j sinh a a R displaystyle lbrace cosh a j sinh a a in R rbrace bolunmus karmasik duzlemde karsilik gelen bir hiperbolik sektorun dilimi icinde sadeceyari alaninda vardir Bolunmus karmasik duzlem geometrisi R R displaystyle R oplus R de ayirt olmadiginda boyle karisiklik surduruluyor olabilir GeometriUnit hyperbola with z 1 mavi eslenik hiperbol ile z 1 yesil ve asimtotlari z 0 kirmizi Minkowski ic carpimi ile iki boyutlu gercek vektor uzayi denen siklikla 1 1 boyutlu ifade edilen Minkowski uzayidir R1 1 Oklid duzlemi R2geometrisi gibi cok karmasik numaralari ile tarif edilebilir Minkowski nin duzlemi R1 1 geometrisi bolunmus kompleks numaralari ile tarif edilebilir Noktalarin kumesidir z z a2 displaystyle z lVert z rVert a 2 R icindeki a her sifirdan farkli bir hiperbol bir sag ve sol dali a 0 ve a 0 den gecerek olusur Durum a 1 birim hiperbol denir Eslenik hiperbol ile verilir z z a2 displaystyle z lVert z rVert a 2 Noktalari seti ile bir ust ve alt gecen dali 0 a ve 0 a Hiperbol ve eslenik hiperbol bos elemanlarinin kumesini olusturan iki kosegen asimptot lara ayrilir z z 0 displaystyle z lVert z rVert 0 Bu iki hat bazen bos koni olarak adlandirilir R2 icinde dik olan ve egimli 1 var bolunmus karmasik sayilar z ve w ise hiperbolik dik oldugu soylenmektedir z w 0 dir Siradan diklik benzer olsa da siradan bir karmasik sayi aritmetik ile bilinen ozellikle de bu durum daha guc algilanir Bu uzay icinde ayni anda kavraminin temelini olusturur Bolunmus karmasik sayilar icin Euler formulu analogu olan exp j8 cosh 8 jsinh 8 displaystyle exp j theta cosh theta j sinh theta Bu icin varken sadece cift gucler oldugu gercegini kullanarak bir guc seri acilimi elde edilebilir icin tum gercek degerleri icin 8 bolunmus karmasik sayil exp j8 norm 1 e sahiptir ve birim hiperbol sag kolu yatiyor Bu l gibi Numaralari ler olarak adlandirilabilir l tarafindan carpilan geometrik yapi korunur L katsayisi 1 sahip oldugu herhangi bir l ile herhangi bir bolunmus karmasik sayi z carparak z ve modulu korunur ve bir hiperbolik donme alarak geometrik yapisini korur kendilerini ve kendisi icin bos koni hiperbolas alarak bir veya bir gibi adlandirilir Modulu veya esdeger ic carpim O 1 1 adli bir grup olusturan korumak bolunmus karmasik duzlemde tum donusumlerin kumesi SO 1 1 formu tarafindan verilen dort ile birlikte bu grup hiperbolik donme olusturur z z displaystyle z mapsto pm z ve z z displaystyle z mapsto pm z Ustel harita exp R SO 1 1 displaystyle exp colon mathbb R to mathrm SO 1 1 exp j8 tarafindan 8 ya gonderilen bir ile kullanilan ustel formul uygulamasi ej 8 ϕ ej8ejϕ displaystyle e j theta phi e j theta e j phi Eger bir cift karmasik sayi z kosegenin bir yatik sekli degil ise z bir dir Matris gosterimleriBolunmus karmasik sayilar z x j y i tarafindan kolayca gosterilebilir z xyyx displaystyle z mapsto begin pmatrix x amp y y amp x end pmatrix bolunmus karmasik sayilarin toplama ve carpimi toplama ve carpim matrisleri tarafindan verilebilir znin modulu mukabil matrisin determinanti tarafindan verilir Bu gosterim icinde iki yuz olarak bolunmus karmasik eslenik matris tarafindan carparak karsilik gelir C 100 1 displaystyle C begin pmatrix 1 amp 0 0 amp 1 end pmatrix herhangi bir gercek sayi a bir tarafindan hiperbolik rotasyon a carpimina karsilik gelen matris ile cosh asinh asinh acosh a displaystyle begin pmatrix cosh a amp sinh a sinh a amp cosh a end pmatrix Dyi sikarak haritalama olarak hiperbolik versorun hareketi Bu ile ilgilidir R2 ye uygulanan s Bolunmus karmasik sayi duzlemi diagonal bazinda z x yȷ displaystyle z x y jmath icin sirali bir x y cifti kullanilarak cagrilabilir ve haritalama yapiyor u v x y 111 1 x y S displaystyle u v x y begin pmatrix 1 amp 1 1 amp 1 end pmatrix x y S Simdi ikinci dereceden formu uv x y x y x2 y2 displaystyle uv x y x y x 2 y 2 dir Ayrica cosh a sinh a 111 1 ea e a displaystyle cosh a sinh a begin pmatrix 1 amp 1 1 amp 1 end pmatrix e a e a boylece iki hiperboller Sile karsikarsiya getirilir ebj displaystyle e bj nin ise bir nin dogrusal donusumu altinda karsilik gelen s u v ru v r r eb displaystyle sigma u v mapsto ru v r quad r e b Burada in konusunu bu baglamda unutmayin Aslinda bolunmus kompleks sayilarin farkli temsillerinin buyuk bir sayidadir bolunmus karmasik sayinin matris gosterimini yukaridaki kosegen gosterim temsil etmektedir Bolunmus karmasik sayilar asagidaki matris gosterimi icin z x y tarafindan verilir Z xyyx displaystyle Z begin pmatrix x amp y y amp x end pmatrix Bu Jordan kuralli formu ile verilen Jz x y00x y displaystyle J z begin pmatrix x y amp 0 0 amp x y end pmatrix burada Z SJzS 1 displaystyle Z SJ z S 1 ve S 1 111 displaystyle S begin pmatrix 1 amp 1 1 amp 1 end pmatrix TarihceBolunmus karmasik sayilar kullanilmasi 1848 uzanir yi ortaya cikardi spinlerin toplamini gosteren temsil bolunmus karmasik sayilar kullanir Clifford simdi adi verilen bir kuaterniyon cebir katsayilari olarak bolunmus karmasik sayilar kullanimi tanitti O ogelere motorlar dendi tan alinan siradan bir karmasik sayinin rotor eylemine paralel bir terimle cagrildi Benzerlik siradan bir fonksiyonlar icin bir kontrast fonksiyonlarina uzatilabilir Yirminci yuzyildan beri bolunmus karmasik carpma yaygin bir uzayzaman planinin bir a destek olarak gorulmustur Bu modelde sayi z x y j icindeki y nanosaniye icindeki x burada ve y olculur bir uzay zamansal planda bir olay temsil eder Gelecekteki olaylarin kadrandaki karsiligi z Ifade hatasi Taninmayan noktalama karakteri lt x bolunmus karmasik polar ayrisma sahip oldugu z reaj displaystyle z rho e aj Model z a bir referans cercevesi ne girerken ve r nanosaniye bekleyerek orijine ulasilabilecegini soyluyor Bolunmus karmasik denklemi eaj ebj e a b j displaystyle e aj e bj e a b j birim hiperbol uzerinde carpim ifadesi dogrudas hizlari icin hizlarin toplanirligini gostermektedir Olaylarin eszamanlilik hiz a ya baglidir z sjeaj s R displaystyle lbrace z sigma je aj sigma in R rbrace a hizli referans cercevesinde orijin eszamanli olaylarin hattidir Iki olay z ve w oldugunda z w zw 0 Kanonik olaylar exp aj vej exp aj orijini ile eszamanli olaylari j exp aj ile orantili oldugu referans cercevesinin eksende dik hiperbolik ve Lie dir 1 935 J C Vignaux ve A Duranona y Vedia Contribucion bir las Ciencias Fisicas y Matematicas Republica Argentina in Spanish dort makalelerde bolunmus Geometrik cebir ve fonksiyonlar teorisi gelistirdi Bu aciklayici ve pedagojik denemeleri genis takdir icin konu sundu 1941 yilinda EF Allen zz 1 icinde yazili bir ucgenin dokuz nokta bir hiperbol kurmak icin bolunmus Geometrik aritmetik kullanilir 1956 yilinda Mieczyslaw Warmus Bulletin de l Academie Polanaise des Sciences te Yaklasikliklar Hesabi Referanslar baglantiya bakiniz yayinladi O bolunmus karmasik sayi ile bir a A tespit z A a2 ȷ A a2 displaystyle z frac A a 2 jmath frac A a 2 ve bir yaklasik sayi olarak nitelendirdi Matematiksel Yorumlar Mathematical Reviews 1961 yilinda Warmus araliginin orta noktasi ve yaricapi ifade olarak yaklasik sayida bilesenleri atifta bulunarak onun fuar devam etti EsanlamlilarFarkli otorler cift kompleks sayilar icin isimlerin buyuk bir cesitliligini kullandi Bunlardan bazilari sunlardir gercek tessarines James Cockle 1848 cebrik motorlar W K Clifford 1882 hiperbolik kompleks sayilar J C Vignaux 1935 ciftgercek sayilar U Bencivenga 1946 yaklasik sayilar Warmus 1956 for use in countercomplex veya hyperbolic numbers from ikikat sayilar 1968 and 1990 anormal kompleks sayilar W Benz 1973 kafakaristirici sayilar P Fjelstad 1986 and Poodiack amp LeClair 2009 Lorentz sayilari F R Harvey 1990 hiperbolik sayilar G Sobczyk 1995 yari karmasik sayilar F Antonuccio 1994 bolunmus karmasik sayilar B Rosenfeld 1997 uzayzaman sayilari N Borota 2000 ikizkarmasik sayilar S Olariu 2002 Bolunmus karmasik sayilar ve yuksek boyutlu iliskiler ler esdordeyler ve zaman zaman Musean Sayilar olarak adlandirilmistir oyle ki in gelistirdigi in bir alt kumesidir Ayrica bakinizMinkowski uzayi Bir modifiye ile elde edilen bolunmus karmasik sayilar daha yuksek mertebeden turevler veya es dordey Lie Teorik olarak daha soyut bir genelleme olusur Cebir ve sayilar programlari zarfi Lie cebiri Ozel gorelilikKaynaklar ve Dis baglantilarFrancesco Antonuccio 1994 Semi complex analysis and mathematical physics22 Agustos 2016 tarihinde Wayback Machine sitesinde Bencivenga Uldrico 1946 Sulla rappresentazione geometrica della algebra doppie dotate di modulo Atti della real academie della scienze e belle lettre di Napoli Ser 3 v 2 No7 MR0021123 Benz W 1973 Vorlesungen uber Geometrie der Algebren Springer N A Borota E Flores and T J Osler 2000 Spacetime numbers the easy way 34 159 168 N A Borota and T J Osler 2002 Functions of a spacetime variable Mathematics and Computer Education 36 231 239 K Carmody 1988 Circular and hyperbolic quaternions octonions and sedenions Appl Math Comput 28 47 72 K Carmody 1997 Circular and hyperbolic quaternions octonions and sedenions further results Appl Math Comput 84 27 48 F Catoni D Boccaletti R Cannata V Catoni E Nichelatti P Zampetti 2008 The Mathematics of Minkowski Space Time Basel Chapter 4 Trigonometry in the Minkowski plane ISBN 978 3 7643 8613 9 Cockle James 1848 A New Imaginary in Algebra London Edinburgh Dublin Philosophical Magazine 3 33 435 9 Clifford W K Mathematical Works 1882 edited by A W Tucker pp 392 Further Notes on De Boer R 1987 An also known as list for perplex numbers American Journal of Physics 55 4 296 Fjelstadt P 1986 Extending Special Relativity with Perplex Numbers American Journal of Physics 54 416 F Reese Harvey Spinors and calibrations Academic Press San Diego 1990 ISBN 0 12 329650 1 Contains a description of normed algebras in indefinite signature including the Lorentz numbers Hazewinkle M 1994 Double and dual numbers Encyclopaedia of Mathematics Soviet AMS Kluwer Dordrect 1985 Transformations in Special Relativity International Journal of Theoretical Physics 24 223 36 C Muses Applied hypernumbers Computational concepts Appl Math Comput 3 1977 211 226 C Muses Hypernumbers II Further concepts and computational applications Appl Math Comput 4 1978 45 66 Olariu Silviu 2002 Complex Numbers in N Dimensions Chapter 1 Hyperbolic Complex Numbers in Two Dimensions pages 1 16 North Holland Mathematics Studies 190 Elsevier ISBN 0 444 51123 7 Poodiack Robert D amp Kevin J LeClair 2009 Fundamental theorems of algebra for the perplexes 40 5 322 35 Rosenfeld B 1997 Geometry of Lie Groups Kluwer Academic Pub Sobczyk G 1995 Hyperbolic Number Plane13 Kasim 2013 tarihinde Wayback Machine sitesinde also published in 26 268 80 Vignaux J 1935 Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel Contribucion al Estudio de las Ciencias Fisicas y Matematicas Universidad Nacional de la Plata Republica Argentina M Warmus 1956 Calculus of Approximations 9 Mart 2012 tarihinde Wayback Machine sitesinde Bulletin de l Academie Polonaise de Sciences Vol 4 No 5 pp 253 257 Yaglom I 1968 Complex Numbers in Geometry translated by E Primrose from 1963 Russian original Academic Press N Y pp 18 20
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State