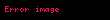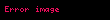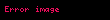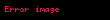İstatistik bilim dalında Kruskal-Wallis sıralamalı tek yönlü varyans analizi, bağımsız gruplar arası anakütle medyanlarının eşitliğini sınamak amacı ile kullanılan bir parametrik olmayan istatistik sınamasıdır. Adı bu yöntemi ilk defa ortaya koyan ve atıfla konmuştur. Matematiksel olarak ayrı olmakla beraber, tek yönlü varyans analizinin bir değişik şekli olarak görülebilir. Diğer bir görüşe göre Mann-Whitney U sınamasının 3 veya daha çoklu gruplara genişletilmesidir.
Kruskal-Wallis sıralamalı tek yönlü varyans analizinin amacı içinde tane grup bulunan bir anakütlenin grup medyanlarının eşit olup olmadığını araştırmaktır. Parametrik olmayan istatistik oladuğu için Kruskal-Wallis sınaması anakütlenin normal dağılım gösterdiğini varsaymamaktadır ve bu nedenle şeklen benzeri olan tek yönlü varyans analizinden değişiktir.
Ama bu sınama için yapılan ana varsayım incelenen her anakütle grubunun, grup medyan değerlerindeki farklılık dışında, ayni dağılım gösterdiğidir.
Sıfır ve karşıt hipotezler
Problem için sıfır hipotezi
- H0 : g grup medyanları birbirine eşittir.
Bu sıfır hipotezi kullanılan analizi yani hipotez sınama kuralları kullanılarak kabul veya red edilecektir. Kruskal-Walis sınaması bir tek yönlü varyans analizinin analogu olduğu için, biraz karmaşıktır. Karşıt hipotez '
- H1: Bazı grup medyanları birbirine eşit değildir
şeklinde ifade edilir. Bu demektir ki sıfır hipotez red edilince kesin anlamlı bir sonuç ortaya çıkmamaktadır. Ya bütün grup medyanları birbirine eşit değildir yahut da bazı grup medyanları eşit değildir yani bazıları birbirine eşittir. Hangilerinin birbirlerine eşit olduğunu bulmak için varyanslar analizinde çoklu karşılaştırmalar analizi adı altında bir sıra istatistiksel yöntem geliştirilmiştir.
Örneklem verileri ve sıralama düzeni
Örneklem ham verileri şunlardır:
bütün grupları kapsayan toplam gözlem sayısı;
sayıda grup bulunur ve veriler gruplara göre belirtilmiştir;
her bir grup i için toplam gözlem sayısı i=1,...g.
i=1...
j=1,...,g,. Her grup için ayrılmış toplam N tane veri.
Bu ham örneklem verilerinin dönüştürülüp genel sıralama düzeni verileri haline getirilmesi gereklidir. Grup üyeliğini bir kenara bırakarak tüm grupları birlikte alarak bütün veri değerlerini, yani 1 ile N sayıda veri değeri, sıralama düzenine konulur. Burada beraberlik gösteren veri değerlerine uygulanan en uygun strateji beraberlik gösterenlerin ortalama sıra numarasının kullanılmasıdır ve bu bazen kesirli sıralama numarası ortaya çıkartabilir. Her bir grup verileri için bu genel sıralama numaraları ayrılır ve bunlar analize veri olur.

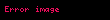
Kruskal-Wallis sınama istatistiği için hesaplar
Önce tüm sıralama düzeni sıralama numaraları (yani tüm 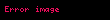

.
Sonra her bir grup (i=1,..g) için sıralama numaraları ayrı ayrı alınarak grup sıralama numaraları ortalamaları (yani 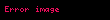
.
Genel Kruskal-Wallis sınama istatistiği (K) şöyle verilir:
Bu genel sınama formülü daha da geliştirilebilir:
Eğer, genel sıralama düzeni beraberlik halinde kullanılan strateji ortalama sıra numaralarını kullanma değilse, bu genel sınama formülü kullanılır. Bu halde beraberlik için bir düzeltme faktörü bulunup kullanılır. Bu beraberlik düzeltme faktörü (BDF) şudur:
.
Burada
- G değişik beraberlikler sayısı;
- ti her beraberlikte bulunan sıralama düzenli veri sayısıdır.
Bu halde beraberlikler için düzeltilmiş genel Kruskal-Wallis test istatistiği
- K* = K / BDF
olur. Ancak pratikten bilinmektedir ki eğer beraberlikler sayısı ve her beraberlikte bulunan sıralama numara sayısı küçükse, bu beraberlik düzeltmesi sınama sonuçlarına çok az etkide bulunur.
Eğer sıralama düzeni kurulurken hiç beraberlik bulunmuyorsa veya beraberlik halinde kullanılan strateji beraberlik sıralamaların ortalaması ise, 
olur. Bu, genel sınama formülüne konulursa Kruskal-Wallis genel sınama istatistiği şöyle ifade edilir:
.
Anlamlılık düzeyi, p-değeri ve sonuç
En son aşama olarak ya bir g-1 serbestlik değerli ki-kare dağılımı icin p-değeri bulmak veya yine g-1 serbestlik değerli ki-kare tablo değerlerini bulmak; bunları anlamlılik değeri ile karşılaştırıp sıfır hipotez hakkında sonuç çıkartamak ve bu sonucu açıklamak gerekir:
Küçük grup veri sayıları
Eğer bazı gruplar için veri sayısı ni küçükse, yani 5 veya 5in altında ise, kullanılacak anlamlılık değerleri Kruskal-Wallis tarafından özel bir tabloda verilmiştir.
Büyük grup veri sayıları
Eğer grup veri sayıları büyük ise, yani hepsi 5den fazla ise, p-değeri yaklaşık olarak
dağılımı gösterir.
Kruskal-Wallis sınama istatistiği K (veya K*) kullanılarak (g-1) serbestlik derecesi için ki-kare dağılımı kullanılarak bir p-değeri bulunabilir. Genellikle p-degeri bulmak için özel bir kompüter ki-kare değer simulasyon programı veya özel bir istatistik paket programı kullanılmasi gerekir.
- Bulunan p-değeri anlamlılık düzeyi yüzdeleri olan %5 veya %1 den daha büyük ise sıfır hipotez olan grup medyanlarinin birbirine eşit olması kabul edilir.
- p-degeri %5den daha küçük fakat %1den büyükse, sonuç pek kesin olmayabilir, ama yine de %5 anlamlılık düzeyinde sıfır hipotez kabul edilir.
- p-değeri %1den küçükse, sıfır hipotezi rededilir.
Diğer bir yaklaşım, p-değeri bulmadan her bir serbestlik derecesi için özel ki-kare dağılımı yukarı kuyruk alanları veren özel ki-kare tablosu kullanma ile ortaya çıkartılır. Bu halde (g-1) serbestlik değeri için %5 ve %1 tablo değerlerine bakılır. Bu tablo degerleri hesaplanmış K değeri ile karşılaştırılır:
- Hesaplanmış K değeri tablo değerinden küçükse, sıfır hipotez kabul edilir.
- Hesaplanmış K değeri tablo değerinden büyükse, sıfır hipotez red edilir.
Sonuç açıklaması
Eğer sıfır hipotez kabul edilirse problem için sonuçlar çok kesin ve anlamlı sayılır. Bu problem için ana varsayım
- 'Anakütlede grup medyanlardan başka her türlü grup özelliği aynıdır.'
olduğu için sıfır hipotez kabul edilmesi daha pratik bir sonuç olarak
- 'anakütledeki gruplar her bakımdan aynıdır veya görülen gruplar aralarında anakütlede hiç fark yoktur.'
sonucu çıkartılabilir.
Eğer sıfır hipotez rededilirse (yani karşıt hipotez kabul edilirse) sonuçlar çok kesin değildir. Aynı parametrik tek yönlü varyans analizi sonucu gibi, bu halde grup medyanlarının hepsi birbirine eşit olmamakla beraber, grup medyanlarının bazılarının birbirine eşit olmaları mümkündür. Bu halde varyanslar analizinde analizi kullanılır.
Ayrıca bakınız
Kaynakça
- ^ William H. Kruskal ve W. Allen Wallis (1952) "Use of ranks in one-criterion variance analysis Journal of the American Statistical Association Cilt 47 No.26 Say. 583–621, [1] 1 Nisan 2010 tarihinde Wayback Machine sitesinde .
- ^ William H. Kruskal ve W. Allen Wallis (1952) "Use of ranks in one-criterion variance analysis Journal of the American Statistical Association Cilt 47 No.26 Say. 614–617, [2] 1 Nisan 2010 tarihinde Wayback Machine sitesinde .
Dışsal kaynaklar
- Sidney Siegel and N. John Castellan, Jr. (1988). Nonparametric Statistics for the Behavioral Sciences (second edition). New York: McGraw-Hill.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Istatistik bilim dalinda Kruskal Wallis siralamali tek yonlu varyans analizi bagimsiz gruplar arasi anakutle medyanlarinin esitligini sinamak amaci ile kullanilan bir parametrik olmayan istatistik sinamasidir Adi bu yontemi ilk defa ortaya koyan ve atifla konmustur Matematiksel olarak ayri olmakla beraber tek yonlu varyans analizinin bir degisik sekli olarak gorulebilir Diger bir goruse gore Mann Whitney U sinamasinin 3 veya daha coklu gruplara genisletilmesidir Kruskal Wallis siralamali tek yonlu varyans analizinin amaci icinde g displaystyle g tane grup bulunan bir anakutlenin grup medyanlarinin esit olup olmadigini arastirmaktir Parametrik olmayan istatistik oladugu icin Kruskal Wallis sinamasi anakutlenin normal dagilim gosterdigini varsaymamaktadir ve bu nedenle seklen benzeri olan tek yonlu varyans analizinden degisiktir Ama bu sinama icin yapilan ana varsayim incelenen her anakutle grubunun grup medyan degerlerindeki farklilik disinda ayni dagilim gosterdigidir Sifir ve karsit hipotezlerProblem icin sifir hipotezi H0 g grup medyanlari birbirine esittir Bu sifir hipotezi kullanilan analizi yani hipotez sinama kurallari kullanilarak kabul veya red edilecektir Kruskal Walis sinamasi bir tek yonlu varyans analizinin analogu oldugu icin biraz karmasiktir Karsit hipotez H1 Bazi grup medyanlari birbirine esit degildir seklinde ifade edilir Bu demektir ki sifir hipotez red edilince kesin anlamli bir sonuc ortaya cikmamaktadir Ya butun grup medyanlari birbirine esit degildir yahut da bazi grup medyanlari esit degildir yani bazilari birbirine esittir Hangilerinin birbirlerine esit oldugunu bulmak icin varyanslar analizinde coklu karsilastirmalar analizi adi altinda bir sira istatistiksel yontem gelistirilmistir Orneklem verileri ve siralama duzeniOrneklem ham verileri sunlardir N displaystyle N butun gruplari kapsayan toplam gozlem sayisi g displaystyle g sayida grup bulunur ve veriler gruplara gore belirtilmistir ni displaystyle n i her bir grup i icin toplam gozlem sayisi i 1 g X ij displaystyle X ij i 1 ni displaystyle n i j 1 g Her grup icin ayrilmis toplam N tane veri Bu ham orneklem verilerinin donusturulup genel siralama duzeni verileri haline getirilmesi gereklidir Grup uyeligini bir kenara birakarak tum gruplari birlikte alarak butun veri degerlerini yani 1 ile N sayida veri degeri siralama duzenine konulur Burada beraberlik gosteren veri degerlerine uygulanan en uygun strateji beraberlik gosterenlerin ortalama sira numarasinin kullanilmasidir ve bu bazen kesirli siralama numarasi ortaya cikartabilir Her bir grup verileri icin bu genel siralama numaralari ayrilir ve bunlar analize veri olur rij displaystyle r ij tum gruplari birlikte alarak tum gozlemler icin verilen siralama numaralari olup her bir i displaystyle i grup icin j displaystyle j sayili siralama numarasidir Kruskal Wallis sinama istatistigi icin hesaplarOnce tum siralama duzeni siralama numaralari yani tum rij displaystyle r ij icin tum siralama numaralari ortalamasi r displaystyle bar r alinir Formul su olur r N 1 2 displaystyle bar r N 1 2 Sonra her bir grup i 1 g icin siralama numaralari ayri ayri alinarak grup siralama numaralari ortalamalari yani r i displaystyle bar r i cdot i 1 g bulunur Her bir grup icin formul sudur r i j 1nirijni displaystyle bar r i cdot frac sum j 1 n i r ij n i Genel Kruskal Wallis sinama istatistigi K soyle verilir K N 1 i 1gni r i r 2 i 1g j 1ni rij r 2 displaystyle K N 1 frac sum i 1 g n i bar r i cdot bar r 2 sum i 1 g sum j 1 n i r ij bar r 2 Bu genel sinama formulu daha da gelistirilebilir Eger genel siralama duzeni beraberlik halinde kullanilan strateji ortalama sira numaralarini kullanma degilse bu genel sinama formulu kullanilir Bu halde beraberlik icin bir duzeltme faktoru bulunup kullanilir Bu beraberlik duzeltme faktoru BDF sudur BDF 1 i 1G ti3 ti N3 N displaystyle BDF 1 frac sum i 1 G t i 3 t i N 3 N Burada G degisik beraberlikler sayisi ti her beraberlikte bulunan siralama duzenli veri sayisidir Bu halde beraberlikler icin duzeltilmis genel Kruskal Wallis test istatistigi K K BDF olur Ancak pratikten bilinmektedir ki eger beraberlikler sayisi ve her beraberlikte bulunan siralama numara sayisi kucukse bu beraberlik duzeltmesi sinama sonuclarina cok az etkide bulunur Eger siralama duzeni kurulurken hic beraberlik bulunmuyorsa veya beraberlik halinde kullanilan strateji beraberlik siralamalarin ortalamasi ise K displaystyle K genel formulu icin paydayi basitlestirebilme imkani vardir Dikkat edilirse payda 1 N tam sayilarinin toplamina esit olur ve bu toplam icin bir ozel formule gore bu toplam hesaplanabilir Boylece formul paydasi i 1g j 1ni rij r 2 N 1 N N 1 12 displaystyle sum i 1 g sum j 1 n i r ij bar r 2 N 1 N N 1 12 olur Bu genel sinama formulune konulursa Kruskal Wallis genel sinama istatistigi soyle ifade edilir K 12N N 1 i 1gni r i r 2 displaystyle K frac 12 N N 1 sum i 1 g n i bar r i cdot bar r 2 Anlamlilik duzeyi p degeri ve sonucEn son asama olarak ya bir g 1 serbestlik degerli ki kare dagilimi icin p degeri bulmak veya yine g 1 serbestlik degerli ki kare tablo degerlerini bulmak bunlari anlamlilik degeri ile karsilastirip sifir hipotez hakkinda sonuc cikartamak ve bu sonucu aciklamak gerekir Kucuk grup veri sayilari Eger bazi gruplar icin veri sayisi ni kucukse yani 5 veya 5in altinda ise kullanilacak anlamlilik degerleri Kruskal Wallis tarafindan ozel bir tabloda verilmistir Buyuk grup veri sayilari Eger grup veri sayilari buyuk ise yani hepsi 5den fazla ise p degeri yaklasik olarak Pr xg 12 K displaystyle Pr chi g 1 2 geq K dagilimi gosterir Kruskal Wallis sinama istatistigi K veya K kullanilarak g 1 serbestlik derecesi icin ki kare dagilimi kullanilarak bir p degeri bulunabilir Genellikle p degeri bulmak icin ozel bir komputer ki kare deger simulasyon programi veya ozel bir istatistik paket programi kullanilmasi gerekir Bulunan p degeri anlamlilik duzeyi yuzdeleri olan 5 veya 1 den daha buyuk ise sifir hipotez olan grup medyanlarinin birbirine esit olmasi kabul edilir p degeri 5den daha kucuk fakat 1den buyukse sonuc pek kesin olmayabilir ama yine de 5 anlamlilik duzeyinde sifir hipotez kabul edilir p degeri 1den kucukse sifir hipotezi rededilir Diger bir yaklasim p degeri bulmadan her bir serbestlik derecesi icin ozel ki kare dagilimi yukari kuyruk alanlari veren ozel ki kare tablosu kullanma ile ortaya cikartilir Bu halde g 1 serbestlik degeri icin 5 ve 1 tablo degerlerine bakilir Bu tablo degerleri hesaplanmis K degeri ile karsilastirilir Hesaplanmis K degeri tablo degerinden kucukse sifir hipotez kabul edilir Hesaplanmis K degeri tablo degerinden buyukse sifir hipotez red edilir Sonuc aciklamasi Eger sifir hipotez kabul edilirse problem icin sonuclar cok kesin ve anlamli sayilir Bu problem icin ana varsayim Anakutlede grup medyanlardan baska her turlu grup ozelligi aynidir oldugu icin sifir hipotez kabul edilmesi daha pratik bir sonuc olarak anakutledeki gruplar her bakimdan aynidir veya gorulen gruplar aralarinda anakutlede hic fark yoktur sonucu cikartilabilir Eger sifir hipotez rededilirse yani karsit hipotez kabul edilirse sonuclar cok kesin degildir Ayni parametrik tek yonlu varyans analizi sonucu gibi bu halde grup medyanlarinin hepsi birbirine esit olmamakla beraber grup medyanlarinin bazilarinin birbirine esit olmalari mumkundur Bu halde varyanslar analizinde analizi kullanilir Ayrica bakinizMann Whitney U sinamasiKaynakca William H Kruskal ve W Allen Wallis 1952 Use of ranks in one criterion variance analysisJournal of the American Statistical Association Cilt 47 No 26 Say 583 621 1 1 Nisan 2010 tarihinde Wayback Machine sitesinde William H Kruskal ve W Allen Wallis 1952 Use of ranks in one criterion variance analysisJournal of the American Statistical Association Cilt 47 No 26 Say 614 617 2 1 Nisan 2010 tarihinde Wayback Machine sitesinde Dissal kaynaklarSidney Siegel and N John Castellan Jr 1988 Nonparametric Statistics for the Behavioral Sciences second edition New York McGraw Hill
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans