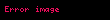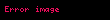Olasılık kuramı ve istatistik bilim dallarında ki-kare dağılım (x2 dağılımı) özellikle çıkarımsal istatistik analizde çok geniş bir pratik kullanım alanı bulmuştur.
Olasılık yoğunluk fonksiyonu | |
Yığmalı dağılım fonksiyonu | |
| Parametreler | serbestlik derecesi |
|---|---|
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | yaklaşık olarak |
| Mod | eğer |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | eğer |
| Karakteristik fonksiyon | |
Bu dağılım, gamma dağılımından elde edilir.
x, ve n parametreleri ile gamma dağılımına sahip olsun:
olur.
Burada ve alınırsa, elde edilen yeni dağılıma, serbestlik derecesiyle ki-kare dağılımı denir ve ile gösterilir.
x, serbestlik derecesiyle ki-kare dağılımına sahip ise:
ki-kare 1 n(0.1)'e eşittir olur.
Teorem 1
ise olur.
Teorem 2
rassal değişkenler N(0,1) dağılımına sahip olsun.
ise olur.
Teorem 3
varyansı bilinen, dağılımına sahip rastgele örneklem ve örneklem varyansı olmak üzere:
olur.
Karakteristikleri
Olasılık yoğunluk fonksiyonu
Ki-kare dağılım için olasılık yoğunluk fonksiyonu şu olur:
Burada 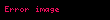
Yığmalı dağılım fonksiyonu
Ki-kare dağılımının yığmalı dağılım fonksiyonu şudur:
burada 

Ki-karenin için verilen tablolar (biri aşağıda verilmiştir) yığmalı dağılim fonksiyonundan elde edilmektedir. Bu tablolar birçok değişik kaynaklardan bulunabilir. Örneğin bu fonksiyon için tablolar spreadsheet ve bulunmaktadır.
Karakteristik fonksiyonu
Ki-kare dağılımının karakteristik fonksiyonu şöyle yazılır:
Özellikleri
- Ki-kare dağılımı analizde epeyce kullanış alanı bulmuştur. Parametrik istatistik olarak varyans değeri güvenlik aralığı ve hipotez testi, parametrik olamayan uygunluk iyiliği testi, olumsallık tablosu üzerinde bağımsızlık testi ve ki-kareye bağlı ortaklılık katsayıları, uzaklık ölçüleri vb.
- iki ki-kare dağılımının oranından ortaya çıkması dolayışıyla önemli rol oynamaktadır.
Normal yaklaşım
Eğer 




Fisher ispat etmiştir ki 

Aynı normal yaklaşım sonucuna moment karşılaştırması yapılarak da erişilebilir. Bunu görmek için ki-dağılım gösteren rassal değişken 
ve
Burada 



Sonra basitleşen moment karşılaştırılması sonuçları şu yaklaşık 
,
Bundan da şu ifade hemen çıkartılabilir\:
.
Wilson ve Hilferty [1931] göstermiştir ki 




Eğer serbestlik derecesi 2 ise üstel dağılım ile aynı dağılımdır.
Enformasyon entropisi
ifadesi şöyle verilir:
Burada 
İlişkili dağılımlar
- Serbestlik derecesi 2ye eşit olan
için
bir üstel dağılım olur.
- Normal dağılım gösteren ve birbirinden bağımsız olan
değişkenleri için
ise,
bir ki-kare dağılımı gösterir.
- Eğer
dağılımlarının sıfır olmayan ortalamaları varsa, o halde
bir çıkartılmıştır.
olduğundan dolayı, ki-kare dağılımı
bir gamma dağılımının özel halidir.
- Eğer verilmiş serbestlik dereceleri ile
ve
birbirinden bağımsız iken
ise,
bir F-dağılımı gösterir.
ifadesi için
değişkenleri bağımsız ve
ise, o halde
ifadesi bir ki-kare dağılımı gösterir.
- Eğer
ki-kare dağılımı gösterirse, o halde
ifadesi de ki-kare dağılımı gösterir.
- Özellikle, eğer
(yani 2 serbestlik derecesi gösteren ki-kare ise), o halde
ifadesi Rayleigh dağılımı gösterir.
- Eğer
, yani hepsi
normal dağılım gösteren, rassal değişkenlerse, o halde
olur; burada 
- Eğer
, ise, o halde
olur.
| İsim | İstatistik |
|---|---|
| Ki-kare dağılımı |  |
 | |
 | |
 |
Ki kare kritik değerler tablosu
g serbestlik derecesi için yukarı kuyruk alanının (olasılığın) α olmasına karşıt olan ki2 kritik değeri
+-----+-----------------------------------------------------------------------+ | \ α| | | \ | 0.995 0.91 0.925 0.95 0.90 0.10 0.05 0.025 0.01 0.005 | |g \ | | +-----+-----------------------------------------------------------------------+ | 1 | 0.00 0.00 0.00 0.00 0.02 2.71 3.84 5.02 6.63 7.88 | | 2 | 0.01 0.02 0.05 0.10 0.21 4.61 5.99 7.38 9.21 10.60 | | 3 | 0.07 0.11 0.22 0.35 0.58 6.25 7.81 9.35 11.34 12.84 | | 4 | 0.21 0.30 0.48 0.71 1.06 7.78 9.49 11.14 13.28 14.86 | | 5 | 0.41 0.55 0.83 1.15 1.61 9.24 11.07 12.83 15.09 16.75 | | 6 | 0.68 0.87 1.24 1.64 2.20 10.64 12.59 14.45 16.81 18.55 | | 7 | 0.99 1.24 1.69 2.17 2.83 12.02 14.07 16.01 18.48 20.28 | | 8 | 1.34 1.65 2.18 2.73 3.49 13.36 15.51 17.53 20.09 21.95 | | 9 | 1.73 2.09 2.70 3.33 4.17 14.68 16.92 19.02 21.67 23.59 | | 10 | 2.16 2.56 3.25 3.94 4.87 15.99 18.31 20.48 23.21 25.19 | | 11 | 2.60 3.05 3.82 4.57 5.58 17.28 19.68 21.92 24.72 26.76 | | 12 | 3.07 3.57 4.40 5.23 6.30 18.55 21.03 23.34 26.22 28.30 | | 13 | 3.57 4.11 5.01 5.89 7.04 19.81 22.36 24.74 27.69 29.82 | | 14 | 4.07 4.66 5.63 6.57 7.79 21.06 23.68 26.12 29.14 31.32 | | 15 | 4.60 5.23 6.26 7.26 8.55 22.31 25.00 27.49 30.58 32.80 | | 16 | 5.14 5.81 6.91 7.96 9.31 23.54 26.30 28.85 32.00 34.27 | | 17 | 5.70 6.41 7.56 8.67 10.09 24.77 27.59 30.19 33.41 35.72 | | 18 | 6.26 7.01 8.23 9.39 10.86 25.99 28.87 31.53 34.81 37.16 | | 19 | 6.84 7.63 8.91 10.12 11.65 27.20 30.14 32.85 36.19 38.58 | | 20 | 7.43 8.26 9.59 10.85 12.44 28.41 31.41 34.17 37.57 40.00 | | 21 | 8.03 8.90 10.28 11.59 13.24 29.62 32.67 35.48 38.93 41.40 | | 22 | 8.64 9.54 10.98 12.34 14.04 30.81 33.92 36.78 40.29 42.80 | | 23 | 9.26 10.20 11.69 13.09 14.85 32.01 35.17 38.08 41.64 44.18 | | 24 | 9.89 10.86 12.40 13.85 15.66 33.20 36.42 39.36 42.98 45.56 | | 25 | 10.52 11.52 13.12 14.61 16.47 34.38 37.65 40.65 44.31 46.93 | | 26 | 11.16 12.20 13.84 15.38 17.29 35.56 38.89 41.92 45.64 48.29 | | 27 | 11.81 12.88 14.57 16.15 18.11 36.74 40.11 43.19 46.96 49.64 | | 28 | 12.46 13.56 15.31 16.93 18.94 37.92 41.34 44.46 48.28 50.99 | | 29 | 13.12 14.26 16.05 17.71 19.77 39.09 42.56 45.72 49.59 52.34 | | 30 | 13.79 14.95 16.79 18.49 20.60 40.26 43.77 46.98 50.89 53.67 | +-----+-----------------------------------------------------------------------+
Kaynak: Kritik değerler İtalyanca Wikipedia için serbest programının qchisq(,1:30) fonksiyonu kullanılarak bulunmuştur.
Serbestlik derecesi g>30 olursa kritik değerleri bulmak için şu ifadeyi kullanmak yeterli olacaktır.
- χ²α,g = 1/2 ( zα + √(2g-1) )²
Burada zα Standart Normal N(0,1) için kritik değerdir (örneğin z0,95 = 1,645 olur.)
Ayrıca bakınız
- Serbestlik derecesi (istatistik)
- birleştirmek için
Kaynakça
- ^ (PDF). 15 Ekim 2008 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 6 Nisan 2008.
Dış bağlantılar
- Ki-kare uyum-iyiliği sınaması ders notları 3 Mart 2008 tarihinde Wayback Machine sitesinde .
Yale University Stats 101 kodlu ders için ornekler hipotez sinamasi ve parametre tahminleri konularini kapsar.
- , Richard Lowry'nin istatistik web sitesinde.
- Dağılımlar hesaplayıcısı29 Ocak 2007 tarihinde Wayback Machine sitesinde . Normal, Student'in t, ki-kare ve F dağılımları için olasılıkları ve kritik değerleri hesaplar.
- Ki-kare kritik değerleri için Ki-kare hesaplayıcısı 24 Şubat 2008 tarihinde Wayback Machine sitesinde . South Carolina Universitesi'nde R.Webster West'in Java applet deposunda
- GraphPad tarafından hazırlanmış Ki-kare hesaplayıcısı 3 Aralık 2008 tarihinde Wayback Machine sitesinde .
- Ki-kare dağılımı için tablo 3 Aralık 2007 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve istatistik bilim dallarinda ki kare dagilim x2 dagilimi ozellikle cikarimsal istatistik analizde cok genis bir pratik kullanim alani bulmustur ki kare Olasilik yogunluk fonksiyonuYigmali dagilim fonksiyonuParametreler k gt 0 displaystyle k gt 0 serbestlik derecesix 0 displaystyle x in 0 infty Olasilik yogunluk fonksiyonu OYF 1 2 k 2G k 2 xk 2 1e x 2 displaystyle frac 1 2 k 2 Gamma k 2 x k 2 1 e x 2 Birikimli dagilim fonksiyonu YDF g k 2 x 2 G k 2 displaystyle frac gamma k 2 x 2 Gamma k 2 Ortalama k displaystyle k Medyan yaklasik olarak k 2 3 displaystyle k 2 3 Mod k 2 displaystyle k 2 eger k 2 displaystyle k geq 2 Varyans 2k displaystyle 2 k Carpiklik 8 k displaystyle sqrt 8 k Fazladan basiklik 12 k displaystyle 12 k Entropi k2 ln 2G k 2 1 k 2 ps k 2 displaystyle frac k 2 ln 2 Gamma k 2 1 k 2 psi k 2 Moment ureten fonksiyon mf 1 2t k 2 displaystyle 1 2 t k 2 eger 2t lt 1 displaystyle 2 t lt 1 Karakteristik fonksiyon 1 2it k 2 displaystyle 1 2 i t k 2 Bu dagilim gamma dagilimindan elde edilir x l displaystyle lambda ve n parametreleri ile gamma dagilimina sahip olsun f x 1lnG n xn 1e xl x gt 0 displaystyle f x frac 1 lambda n Gamma n x n 1 e frac x lambda qquad x gt 0 olur Burada l 2 displaystyle lambda 2 ve n n 2 displaystyle n nu 2 alinirsa elde edilen yeni dagilima n displaystyle nu serbestlik derecesiyle ki kare dagilimi denir ve Xn2 displaystyle mathrm X nu 2 ile gosterilir x n displaystyle nu serbestlik derecesiyle ki kare dagilimina sahip ise ki kare 1 n 0 1 e esittir f x 12n2G n2 xn2 1e x 2 x gt 0 displaystyle f x frac 1 2 frac nu 2 Gamma frac nu 2 x frac nu 2 1 e x 2 qquad x gt 0 olur Teorem 1 x N 0 1 displaystyle x sim N 0 1 ise x2 X12 displaystyle x 2 sim mathrm X 1 2 olur Teorem 2 x1 x2 xn displaystyle x 1 x 2 cdots x n rassal degiskenler N 0 1 dagilimina sahip olsun y i 1nxi2 displaystyle y sum i 1 n x i 2 ise y Xn2 displaystyle y sim mathrm X n 2 olur Teorem 3 s2 displaystyle sigma 2 varyansi bilinen N m s2 displaystyle N mu sigma 2 dagilimina sahip rastgele orneklem x1 x2 xn displaystyle x 1 x 2 cdots x n ve s2 displaystyle s 2 orneklem varyansi olmak uzere n 1 s2s2 Xn 12 displaystyle frac n 1 s 2 sigma 2 sim mathrm X n 1 2 olur KarakteristikleriOlasilik yogunluk fonksiyonu Ki kare dagilim icin olasilik yogunluk fonksiyonu su olur f x k 12k 2G k 2 x k 2 1e x 2eger x gt 0 0eger x 0 displaystyle f x k begin cases displaystyle frac 1 2 k 2 Gamma k 2 x k 2 1 e x 2 amp text eger x gt 0 0 amp text eger x leq 0 end cases Burada G displaystyle Gamma bir bulundugunu gosterir ve bu gosterir Yigmali dagilim fonksiyonu Ki kare dagiliminin yigmali dagilim fonksiyonu sudur F x k g k 2 x 2 G k 2 P k 2 x 2 displaystyle F x k frac gamma k 2 x 2 Gamma k 2 P k 2 x 2 burada g k z displaystyle gamma k z ve P k z displaystyle P k z ise olur Ki karenin icin verilen tablolar biri asagida verilmistir yigmali dagilim fonksiyonundan elde edilmektedir Bu tablolar bircok degisik kaynaklardan bulunabilir Ornegin bu fonksiyon icin tablolar spreadsheet ve bulunmaktadir Karakteristik fonksiyonu Ki kare dagiliminin karakteristik fonksiyonu soyle yazilir x t k 1 2it k 2 displaystyle chi t k 1 2it k 2 OzellikleriKi kare dagilimi analizde epeyce kullanis alani bulmustur Parametrik istatistik olarak varyans degeri guvenlik araligi ve hipotez testi parametrik olamayan uygunluk iyiligi testi olumsallik tablosu uzerinde bagimsizlik testi ve ki kareye bagli ortaklilik katsayilari uzaklik olculeri vb iki ki kare dagiliminin oranindan ortaya cikmasi dolayisiyla onemli rol oynamaktadir Normal yaklasim Eger X xk2 displaystyle X sim chi k 2 ise limitte k displaystyle k sonsuzluga yaklastikca X displaystyle X normal dagilima yaklasir Ancak bu egilim carpiklik 8 k displaystyle sqrt 8 k ve basiklik fazlaligi 12 k displaystyle 12 k oldugundan dolayi yavas gelismektedir Ki kare dagiliminin iki degisik donusum fonksiyonu normallige cok daha hizla yaklasma gostermektedir Fisher ispat etmistir ki 2X displaystyle sqrt 2X ifadesi yaklasik olarak ortalamasi 2k 1 displaystyle sqrt 2k 1 olan ve varyans degeri 1 olan bir normal dagilim gosterir Ayni normal yaklasim sonucuna moment karsilastirmasi yapilarak da erisilebilir Bunu gormek icin ki dagilim gosteren rassal degisken z X displaystyle z sqrt X in ortalamasi ve varyansi izlensin Bunlar sirasiyla soyle verilir mz 2G k 2 1 2 G k 2 displaystyle mu z sqrt 2 frac Gamma left k 2 1 2 right Gamma left k 2 right ve sz2 k mz2 displaystyle sigma z 2 k mu z 2 Burada G displaystyle Gamma cdot bir Gamma fonksiyonudur mz displaystyle mu z ifadeli gamma fonksiyonunun ozel orani particular ratio su seri halinde acilabilir G N 1 2 G N N 1 18N 1128N2 51024N3 2132768N4 displaystyle frac Gamma left N 1 2 right Gamma left N right sqrt N left 1 frac 1 8N frac 1 128N 2 frac 5 1024N 3 frac 21 32768N 4 ldots right N 1 displaystyle N gg 1 oldugu halde bu oran icin soyle yaklasim bulunur G N 1 2 G N N 1 18N N 1 14N 0 5 N 1 4 displaystyle frac Gamma left N 1 2 right Gamma left N right approx sqrt N left 1 frac 1 8N right approx sqrt N left 1 frac 1 4N right 0 5 sqrt N 1 4 Sonra basitlesen moment karsilastirilmasi sonuclari su yaklasik z displaystyle z dagilimi verirler z N k 1 2 12 displaystyle z sim mathcal N left sqrt k 1 2 frac 1 2 right Bundan da su ifade hemen cikartilabilir 2X N 2k 1 1 displaystyle sqrt 2X sim mathcal N left sqrt 2k 1 1 right Wilson ve Hilferty 1931 gostermistir ki X k3 displaystyle sqrt 3 X k ifadesi ortalamasi 1 2 9k displaystyle 1 2 9k ve varyansi 2 9k displaystyle 2 9k olan bir normal dagilima yaklasiktir k displaystyle k serbestlik derecesi olan bir ki kare dagilimi gosteren bir rassal degisken icin beklenen deger k displaystyle k olur Ayni dagilimin medyan degeri yaklasik olarak su ifade ile verilir k 23 427k 8729k2 displaystyle k frac 2 3 frac 4 27k frac 8 729k 2 Eger serbestlik derecesi 2 ise ustel dagilim ile ayni dagilimdir Enformasyon entropisi ifadesi soyle verilir H f x k ln f x k dx k2 ln 2G k2 1 k2 ps k 2 displaystyle H int infty infty f x k ln f x k dx frac k 2 ln left 2 Gamma left frac k 2 right right left 1 frac k 2 right psi k 2 Burada ps x displaystyle psi x bir Iliskili dagilimlarSerbestlik derecesi 2ye esit olan X x22 displaystyle X sim chi 2 2 icin X Ustel l 12 displaystyle X sim operatorname Ustel left lambda tfrac 1 2 right bir ustel dagilim olur Normal dagilim gosteren ve birbirinden bagimsiz olan Xi N 0 1 displaystyle X i sim N 0 1 degiskenleri icin Y m 1kXm2 displaystyle Y sum m 1 k X m 2 ise Y xk2 displaystyle Y sim chi k 2 bir ki kare dagilimi gosterir Eger Xi N mi 1 displaystyle X i sim N mu i 1 dagilimlarinin sifir olmayan ortalamalari varsa o halde Y m 1kXm2 displaystyle Y sum m 1 k X m 2 bir cikartilmistir X Gamma n2 2 displaystyle X sim operatorname Gamma left tfrac nu 2 2 right oldugundan dolayi ki kare dagilimi X xn2 displaystyle X sim chi nu 2 bir gamma dagiliminin ozel halidir Eger verilmis serbestlik dereceleri ile X1 xn12 displaystyle X 1 sim chi nu 1 2 ve X2 xn22 displaystyle X 2 sim chi nu 2 2 birbirinden bagimsiz iken Y X1 n1X2 n2 displaystyle Y frac X 1 nu 1 X 2 nu 2 ise Y F n1 n2 displaystyle Y sim mathrm F nu 1 nu 2 bir F dagilimi gosterir Y m 1NXm displaystyle Y sum m 1 N X m ifadesi icin Xm x2 nm displaystyle X m sim chi 2 nu m degiskenleri bagimsiz ve n m 1Nnm displaystyle bar nu sum m 1 N nu m ise o halde Y x2 n displaystyle Y sim chi 2 bar nu ifadesi bir ki kare dagilimi gosterir Eger X displaystyle X ki kare dagilimi gosterirse o halde X displaystyle sqrt X ifadesi de ki kare dagilimi gosterir Ozellikle eger X x22 displaystyle X sim chi 2 2 yani 2 serbestlik derecesi gosteren ki kare ise o halde X displaystyle sqrt X ifadesi Rayleigh dagilimi gosterir Eger X1 Xn displaystyle X 1 dots X n yani hepsi N m s2 displaystyle N mu sigma 2 normal dagilim gosteren rassal degiskenlerse o halde i 1n Xi X 2 s2xn 12 displaystyle sum i 1 n X i bar X 2 sim sigma 2 chi n 1 2 olur burada X 1n i 1nXi displaystyle bar X frac 1 n sum i 1 n X i dir Eger X CarpikLogistik 12 displaystyle X sim operatorname CarpikLogistik left tfrac 1 2 right ise o halde log 1 e X x22 displaystyle log 1 e X sim chi 2 2 olur Cesitli ki ve ki kare dagilimlari Isim IstatistikKi kare dagilimi i 1k Xi mi 2si2 displaystyle sum i 1 k frac left X i mu i right 2 sigma i 2 i 1k Xisi 2 displaystyle sum i 1 k left frac X i sigma i right 2 i 1k Xi misi 2 displaystyle sqrt sum i 1 k left frac X i mu i sigma i right 2 i 1k Xisi 2 displaystyle sqrt sum i 1 k left frac X i sigma i right 2 Ki kare kritik degerler tablosug serbestlik derecesi icin yukari kuyruk alaninin olasiligin a olmasina karsit olan ki2 kritik degeri a 0 995 0 91 0 925 0 95 0 90 0 10 0 05 0 025 0 01 0 005 g 1 0 00 0 00 0 00 0 00 0 02 2 71 3 84 5 02 6 63 7 88 2 0 01 0 02 0 05 0 10 0 21 4 61 5 99 7 38 9 21 10 60 3 0 07 0 11 0 22 0 35 0 58 6 25 7 81 9 35 11 34 12 84 4 0 21 0 30 0 48 0 71 1 06 7 78 9 49 11 14 13 28 14 86 5 0 41 0 55 0 83 1 15 1 61 9 24 11 07 12 83 15 09 16 75 6 0 68 0 87 1 24 1 64 2 20 10 64 12 59 14 45 16 81 18 55 7 0 99 1 24 1 69 2 17 2 83 12 02 14 07 16 01 18 48 20 28 8 1 34 1 65 2 18 2 73 3 49 13 36 15 51 17 53 20 09 21 95 9 1 73 2 09 2 70 3 33 4 17 14 68 16 92 19 02 21 67 23 59 10 2 16 2 56 3 25 3 94 4 87 15 99 18 31 20 48 23 21 25 19 11 2 60 3 05 3 82 4 57 5 58 17 28 19 68 21 92 24 72 26 76 12 3 07 3 57 4 40 5 23 6 30 18 55 21 03 23 34 26 22 28 30 13 3 57 4 11 5 01 5 89 7 04 19 81 22 36 24 74 27 69 29 82 14 4 07 4 66 5 63 6 57 7 79 21 06 23 68 26 12 29 14 31 32 15 4 60 5 23 6 26 7 26 8 55 22 31 25 00 27 49 30 58 32 80 16 5 14 5 81 6 91 7 96 9 31 23 54 26 30 28 85 32 00 34 27 17 5 70 6 41 7 56 8 67 10 09 24 77 27 59 30 19 33 41 35 72 18 6 26 7 01 8 23 9 39 10 86 25 99 28 87 31 53 34 81 37 16 19 6 84 7 63 8 91 10 12 11 65 27 20 30 14 32 85 36 19 38 58 20 7 43 8 26 9 59 10 85 12 44 28 41 31 41 34 17 37 57 40 00 21 8 03 8 90 10 28 11 59 13 24 29 62 32 67 35 48 38 93 41 40 22 8 64 9 54 10 98 12 34 14 04 30 81 33 92 36 78 40 29 42 80 23 9 26 10 20 11 69 13 09 14 85 32 01 35 17 38 08 41 64 44 18 24 9 89 10 86 12 40 13 85 15 66 33 20 36 42 39 36 42 98 45 56 25 10 52 11 52 13 12 14 61 16 47 34 38 37 65 40 65 44 31 46 93 26 11 16 12 20 13 84 15 38 17 29 35 56 38 89 41 92 45 64 48 29 27 11 81 12 88 14 57 16 15 18 11 36 74 40 11 43 19 46 96 49 64 28 12 46 13 56 15 31 16 93 18 94 37 92 41 34 44 46 48 28 50 99 29 13 12 14 26 16 05 17 71 19 77 39 09 42 56 45 72 49 59 52 34 30 13 79 14 95 16 79 18 49 20 60 40 26 43 77 46 98 50 89 53 67 Kaynak Kritik degerler Italyanca Wikipedia icin serbest programinin qchisq 1 30 fonksiyonu kullanilarak bulunmustur Serbestlik derecesi g gt 30 olursa kritik degerleri bulmak icin su ifadeyi kullanmak yeterli olacaktir x a g 1 2 za 2g 1 Burada za Standart Normal N 0 1 icin kritik degerdir ornegin z0 95 1 645 olur Ayrica bakinizSerbestlik derecesi istatistik birlestirmek icinKaynakca PDF 15 Ekim 2008 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 6 Nisan 2008 Dis baglantilarKi kare uyum iyiligi sinamasi ders notlari 3 Mart 2008 tarihinde Wayback Machine sitesinde Yale University Stats 101 kodlu ders icin ornekler hipotez sinamasi ve parametre tahminleri konularini kapsar Richard Lowry nin istatistik web sitesinde Dagilimlar hesaplayicisi29 Ocak 2007 tarihinde Wayback Machine sitesinde Normal Student in t ki kare ve F dagilimlari icin olasiliklari ve kritik degerleri hesaplar Ki kare kritik degerleri icin Ki kare hesaplayicisi 24 Subat 2008 tarihinde Wayback Machine sitesinde South Carolina Universitesi nde R Webster West in Java applet deposunda GraphPad tarafindan hazirlanmis Ki kare hesaplayicisi 3 Aralik 2008 tarihinde Wayback Machine sitesinde Ki kare dagilimi icin tablo 3 Aralik 2007 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State