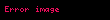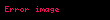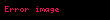Liénard-Wiechert potansiyelleri yüklü bir noktasal parçacığın hareketi esnasında oluşan klasik elektromanyetik etkiyi bir vektör potansiyeli ve bir skaler potansiyel cinsinden ifade eder. Maxwell denklemlerinin doğrudan bir sonucu olarak bu potansiyel relativistik olarak doğru, tam, zamana bağlı etkileri de içeren, noktasal parçacığın hareketine herhangi bir sınır konulmaksızın en genel durum için geçerli olan fakat kuantum mekaniğinin öngördüğü etkileri açıklayamayan elektromanyetik bir alan tanımlar. Dalga hareketi formunda yayılan elektromanyetik ışıma bu potansiyellerden elde edilebilir.
Bu potansiyelin ifadesi kısmî olarak 1898 yılında , bundan bağımsız olarak da 1900 yılında Emil Wiechert tarafından geliştirilmiştir. Potansiyelin genelleştirilmesi göre yapılır.
Hareket eden ve oluşturduğu potansiyellerin açık ifadesi Lienard-Wiechert potansiyelinin noktasal yük ile olan ilişkisiyle aynı ilişki içinde olacak şekilde 1995 yılında Ribarič and Šušteršič tarafından hesaplanmıştır.
Sonuçları
Klasik elektrodinamik Einstein'ın relativite teorisinin gelişmesinde önemli bir rol oynar. Elektromanyetik dalgaların yayılış hareketinin analizi uzay-zamanın özel relativite tarafından açıklanan hâlinin keşfiyle sonuçlanmıştır. Lienard-Wiechert formülasyonunun relativistik hızlarda hareket eden parçacıkların karmaşık analizi açısından önemi büyüktür.
Lienard-Wiechert potansiyelinin çizdiği tablo büyük ölçeklerde doğru olmakla beraber kuantum seviyesindeki deneylerle örtüşmez. Kuantum mekaniği parçacıkların ışımasıyla ilgili kayda değer kısıtlamalar getirir. Lienard-Wiechert formülleriyle belirtilen klasik denklemler gözlemlerle desteklenmiş kuantum mekaniksel fenomenleri açıklayamaz. Örneğin, atomun çevresinde dönen bir elektron bu denklemlere göre ışıma yapması gerekir fakat yapmazlar (bkz. Rydberg formülü). Atomik seviyedeki bu olay enerji durumunun kuantize olmasıyla anlaşılır. 20. yy.ın ileriki onyıllarında kuantum elektrodinamiği kuantum mekaniksel kısıtlamalarla ışıma yapma özelliklerini birleştirmiştir.
Evrensel hız limiti
Elektromanyetik bilginin yayılma hızı olan c (bkz. ışık hızı) sabitinin sonlu olmasından dolayı, belirli bir r noktasında ve t zamanındaki bir parçacığa etki eden kuvvet, kuvvetin kaynağı olan parçacığın t zamanından daha önceki bir tr zamanındaki konumuna bağlıdır. Örneğin, Dünya üzerindeki yüklü bir parçacık Ay'daki parçacığın 1,5 saniye önceki hâlini görür. Bu zaman farkı Güneş ile Dünya arasında yaklaşık 500 saniyedir. Bu önceki tr zamanına denir. Geciktirilmiş zaman pozisyona bağlıdır. Dünya üzerindeki bir parçacık için Ay'ın geciktirilmiş zamanı 1,5 saniye öncesi olurken Güneşinkinin 500 saniye öncesi olması bunu gösterir. Geciktirilmiş zaman, R parçacıkla kaynak arasındaki uzaklık olmak üzere matematiksel olarak aşağıdaki gibi ifade edilir.
Denklemler
Potansiyellerin matematiksel ifadesi
göre A vektörel, 
and
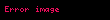

Potansiyellere karşılık gelen elektrik ve manyetik alanlar
Lienard-Wiechert potansiyelleriyle elektrik ve manyetik alanlar doğrudan hesaplanabilir.
Bu hesap birkaç adım gerektirir ve çoğu zaman oldukça karmaşıktır. formunda elektrik ve manyetik alan aşağıdaki gibi yazılabilir.


Formüllerin elde edilişi

Formüllerde
Dirac delta fonksiyonu iken akım ve yük yoğunluklarının ifadesi sırasıyla aşağıdaki gibidir.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Lienard Wiechert potansiyelleri yuklu bir noktasal parcacigin hareketi esnasinda olusan klasik elektromanyetik etkiyi bir vektor potansiyeli ve bir skaler potansiyel cinsinden ifade eder Maxwell denklemlerinin dogrudan bir sonucu olarak bu potansiyel relativistik olarak dogru tam zamana bagli etkileri de iceren noktasal parcacigin hareketine herhangi bir sinir konulmaksizin en genel durum icin gecerli olan fakat kuantum mekaniginin ongordugu etkileri aciklayamayan elektromanyetik bir alan tanimlar Dalga hareketi formunda yayilan elektromanyetik isima bu potansiyellerden elde edilebilir Bu potansiyelin ifadesi kismi olarak 1898 yilinda bundan bagimsiz olarak da 1900 yilinda Emil Wiechert tarafindan gelistirilmistir Potansiyelin genellestirilmesi gore yapilir Hareket eden ve olusturdugu potansiyellerin acik ifadesi Lienard Wiechert potansiyelinin noktasal yuk ile olan iliskisiyle ayni iliski icinde olacak sekilde 1995 yilinda Ribaric and Sustersic tarafindan hesaplanmistir SonuclariKlasik elektrodinamik Einstein in relativite teorisinin gelismesinde onemli bir rol oynar Elektromanyetik dalgalarin yayilis hareketinin analizi uzay zamanin ozel relativite tarafindan aciklanan halinin kesfiyle sonuclanmistir Lienard Wiechert formulasyonunun relativistik hizlarda hareket eden parcaciklarin karmasik analizi acisindan onemi buyuktur Lienard Wiechert potansiyelinin cizdigi tablo buyuk olceklerde dogru olmakla beraber kuantum seviyesindeki deneylerle ortusmez Kuantum mekanigi parcaciklarin isimasiyla ilgili kayda deger kisitlamalar getirir Lienard Wiechert formulleriyle belirtilen klasik denklemler gozlemlerle desteklenmis kuantum mekaniksel fenomenleri aciklayamaz Ornegin atomun cevresinde donen bir elektron bu denklemlere gore isima yapmasi gerekir fakat yapmazlar bkz Rydberg formulu Atomik seviyedeki bu olay enerji durumunun kuantize olmasiyla anlasilir 20 yy in ileriki onyillarinda kuantum elektrodinamigi kuantum mekaniksel kisitlamalarla isima yapma ozelliklerini birlestirmistir Evrensel hiz limitiElektromanyetik bilginin yayilma hizi olan c bkz isik hizi sabitinin sonlu olmasindan dolayi belirli bir r noktasinda ve t zamanindaki bir parcaciga etki eden kuvvet kuvvetin kaynagi olan parcacigin t zamanindan daha onceki bir tr zamanindaki konumuna baglidir Ornegin Dunya uzerindeki yuklu bir parcacik Ay daki parcacigin 1 5 saniye onceki halini gorur Bu zaman farki Gunes ile Dunya arasinda yaklasik 500 saniyedir Bu onceki tr zamanina denir Geciktirilmis zaman pozisyona baglidir Dunya uzerindeki bir parcacik icin Ay in geciktirilmis zamani 1 5 saniye oncesi olurken Gunesinkinin 500 saniye oncesi olmasi bunu gosterir Geciktirilmis zaman R parcacikla kaynak arasindaki uzaklik olmak uzere matematiksel olarak asagidaki gibi ifade edilir tr t Rc displaystyle t r t frac mathcal R c DenklemlerPotansiyellerin matematiksel ifadesi gore A vektorel F displaystyle Phi skaler potansiyel alani belirtmek uzere asagidaki denklemler q yukune sahip hareketli bir noktasal parcacigin Lienard Wiechert potansiyellerini gosterir F x t q R b R ret displaystyle Phi vec x t left frac q R vec beta cdot vec R right rm ret and A x t qb R b R ret displaystyle vec A vec x t left frac q vec beta R vec beta cdot vec R right rm ret b displaystyle vec beta beta parcacigin hizinin c ye bolunmus hali R displaystyle vec R parcacigin pozisyon vektoru ret ifadesi geciktirilmis cozumleri goz onunde bulundurdugumuzu belirtiyor Potansiyellere karsilik gelen elektrik ve manyetik alanlar Lienard Wiechert potansiyelleriyle elektrik ve manyetik alanlar dogrudan hesaplanabilir E F A t displaystyle vec E nabla Phi dfrac partial vec A partial t B A displaystyle vec B nabla times vec A Bu hesap birkac adim gerektirir ve cogu zaman oldukca karmasiktir formunda elektrik ve manyetik alan asagidaki gibi yazilabilir E x t q n b g2 1 b n 3R2 ret qc n n b b 1 b n 3R ret displaystyle vec E vec x t q left frac vec n vec beta gamma 2 1 vec beta cdot vec n 3 R 2 right rm ret frac q c left frac vec n times vec n vec beta times vec dot beta 1 vec beta cdot vec n 3 R right rm ret B n E displaystyle vec B vec n times vec E g displaystyle gamma Lorentz faktoru n displaystyle vec n yukun geciktirilmis pozisyonundan gozlemciye dogru olan birim vektor Formullerin elde edilisir0 t displaystyle mathbf r 0 t pozisyonunda v0 t displaystyle mathbf v 0 t hizinda hareket eden bir parcacik icin yukleri cevreleyen hicbir sinir olmadiginda skaler ve vektorel potansiyellerin geciktirilmis cozumune hareketle ulasilir f r t d t r r c t r r r r t d3r dt displaystyle varphi mathbf r t int delta left t left mathbf r mathbf r right over c t right over left mathbf r mathbf r right rho mathbf r t d 3 r dt A r t d t r r c t r r J r t cd3r dt displaystyle mathbf A mathbf r t int delta left t left mathbf r mathbf r right over c t right over left mathbf r mathbf r right mathbf J mathbf r t over c d 3 r dt Formullerde d t r r c t displaystyle delta left t left mathbf r mathbf r right over c t right Dirac delta fonksiyonu iken akim ve yuk yogunluklarinin ifadesi sirasiyla asagidaki gibidir J r t ev0 t d r r0 t displaystyle mathbf J mathbf r t e mathbf v 0 t delta left mathbf r mathbf r 0 t right r r t ed r r0 t displaystyle rho mathbf r t e delta left mathbf r mathbf r 0 t right Ayrica bakinizKlasik elektromanyetizma Ozel relativite Rydberg formulu Larmor formulu Abraham Lorentz kuvveti
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State