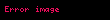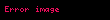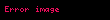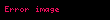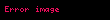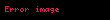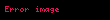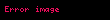Bu madde, uygun değildir. (Ekim 2021) |
Matematikte, Markov Zinciri (Andrey Markov'un adına atfen), sahip bir stokastik süreçtir. Markov özelliğine sahip olmak, mevcut durum verildiğinde, gelecek durumların geçmiş durumlardan bağımsız olması anlamına gelir. Bir başka deyişle, mevcut durumun açıklaması, sürecin gelecekteki evrimini etkileyebilecek tüm bilgiyi kapsar. Gelecek durumlara belirli bir şekilde değil, olasılıksal bir süreçle ulaşılacaktır.
Her bir anda sistem belirli bir olasılık dağılımına bağlı olarak kendi durumunundan başka bir duruma geçebilir yahut aynı durumda kalabilir. Durumda olan değişiklikler geçiş olarak bilinir ve çeşitli durum değişmeleriyle ilişkili olasılıklar da geçiş olasılıkları olarak adlandırılır.
Markov zincirine bir örnek olur. Basit rastgele yürüyüş için durum uzayı bir gösterim üstünde bir grup köşeler halindedir. Geçiş aşamaları ise (yürüyüşün geçmişinde ne olmuş olursa olsun) cari köşeden herhangi bir komşu köşeye gitmeyi kapsar. Cari köşeden herhangi bir komşu köşeye gitme olasılığı hep aynı olup birbirine eşittir.
Tanımı
Markov zincir taşıyan, yani mevcut durum verilmiş olursa geçmiş ve gelecek durumların bağımsız olduğu, ardı ardına gelen, X1, X2, X3, ... ile ifade edilen, bir seri rassal değişkendir. Matematiksel biçimle
Xi'in mümkün değerleri, S olarak ifade edilen ve zincirin durum uzayı adı verilen oluşturur.
Çok kere Markov zincirleri bir ile tanımlanmaktadır ve bu gösterimde kenar doğrular bir durumdan diğer bir duruma geçiş olasılıkları ile tanıtılmaktadır.
Çeşitlemeleri
sürekli bir endeksi bulunur.
Zaman içinde homojen Markov zincirleri zamana göre homojen olan geçiş olasılıkları bulunan Markov zincirleridir ve tüm n değerleri için
olan süreçlerdir.
m sonlu bir sayı ise, bir m dereceli bir Markov zinciri (yani m bellekli bir Markov zinciri) için tüm n değerleri için şu ifadeler verilebilir:
'Klasik' olan (Xn)den yeni bir (Yn) zincirinin şöyle kurulması mümkündür: Yn sıralamalı m-boyutlu X değerlerinden şöyle kurulsun:
- Yn = (Xn, Xn-1, ..., Xn-m+1)
O zaman Yn, durum uzayı Sm olan ve klasik bulunan bir Markov zinciri olur.
Örnek
Markov zincirlerinin özellikleri
İndirgenebilirlik
Dönemsellik
Tekrarlama
Eğer i durumdan başladığımız bilindiği halde, i durumuna hiçbir zaman dönme imkânı yaratmayan bir sıfıra eşit olamayan olasılık bulunuyorsa i durumu geçiş durum olarak nitelendirilir. Daha matematik biçimle ve notasyonla bir rassal değişken olan Ti i durumuna ilk geri dönüş zamanı (vurma zamanı') olsun; yani
Bu halde i durumu geçişli olması için ancak ve ancak
olmalıdır. Eğer bir durum i geçişli değilse (yani 1 olasılıkla bir sonlu olan vurma zamanına sahipse), o halde i durumu yinelenen veya ısrarlı durum olarak adlandırılır. Vurma zamanı sonlu olmakla beraber bir sonlu beklenen değeri bulunması gerekmez. Mi beklenen geri dönüş zamanı, yani
olsun. O halde eğer Mi sonlu ise i durumu da pozitif yinelenen olur; aksi halde i durumu sıfır yinelenen olacaktır; bu durumlara aynı sırayla sıfır olmayan ısrarlı veya sıfır ısrarlı durum adları da verilir.
Bir durumun yinelenen olması
ifadesi gerçekse ortaya çıkacağı ispatlanamıştır.
Eger durum i yi girdikten sonra hiçbir zaman o durumdan çıkmak mümkün değilse, i durumu yutan durum olarak adlandırılır. Bu halde i durumu yutan durum olması için şu koşulu sağlaması gerekir;
and
for
Ergodiklik
P geçiş matrisinde tüm durumlar birbirleri arasında geçiş sağlayabiliyorsa bu zincire ergodik markov zinciri denir.
| 0 | 1 | 0 | 0 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
üstteki P matrisi ergodik bir markov zinciridir.
| 0 | 1 | 0 | 0 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
üstteki P matrisi ise ergodik bir markov zinciri değildir. Sebebi ise 4. duruma hiçbir şekilde varılamamaktadır.
Sonlu durum uzayında Markov zincirleri
Tersinebilir Markov zincirleri
Bernoulli şeması
Genel durum uzayında Markov zincirleri
Uygulamalar
Fizik
Sınama
Kuyruk kuramı
İnternet uygulamaları
Google'in kullandığı internet sayfalarının PageRank'i Markov zinciri ile tanımlanmaktadır. Markov zincirinde durağan dağılımda tüm bilinen internet sayfaları arasından 


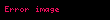
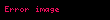


Markov modelleri aynı zamanda kullanıcıların internet gezinti davranışlarını analiz etmek için de kullanılmıştır. Bir kullanıcının bir internet sayfasından web bağlantısı ile geçişi, birincil ya da ikincil Markov modelleri ile modellenebilir ve gelecekteki hareketleri öngörmede ve dolayısıyla internet sayfasını kullanıcı için kişiselleştirme de kullanılabilir.
İstatistik
İktisat
Matematiksel biyoloji
Müzik
Beyzbol
Markov parodi üreticileri
Tarihçe
Ayrıca bakınız
Kaynakça
- ^ ABD patent 6.285.999
- A.A. Markov. "Rasprostranenie zakona bol'shih chisel na velichiny, zavisyaschie drug ot druga". Izvestiya Fiziko-matematicheskogo obschestva pri Kazanskom universitete, 2-ya seriya, tom 15, pp 135–156, 1906.
- A.A. Markov. "Extension of the limit theorems of probability theory to a sum of variables connected in a chain". Yeni basım Appendiks B: R. Howard. Dynamic Probabilistic Systems, volume 1: Markov Chains. John Wiley and Sons, 1971.
- Classical Text in Translation: A. A. Markov, An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains, trans. David Link. Science in Context 19.4 (2006): 591-600. Online: http://journals.cambridge.org/production/action/cjoGetFulltext?fulltextid=637500
- Leo Breiman. Probability. Original edition published by Addison-Wesley, 1968; reprinted by Society for Industrial and Applied Mathematics, 1992. . (See Chapter 7.)
- J.L. Doob. Stochastic Processes. New York: John Wiley and Sons, 1953. .
- S. P. Meyn and R. L. Tweedie. Markov Chains and Stochastic Stability. London: Springer-Verlag, 1993. . online: . Second edition to appear, Cambridge University Press, 2009.
- S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, 2007. . Appendix contains abridged Meyn & Tweedie. online:
- Booth, Taylor L. (1967). Sequential Machines and Automata Theory (1.1 yayıncı = John Wiley and Sons, Inc. bas.). New York. Library of Congress Card Catalog Number 67-25924. Extensive, wide-ranging book meant for specialists, written for both theoretical computer scientists as well as electrical engineers. With detailed explanations of state minimization techniques, FSMs, Turing machines, Markov processes, and undecidability. Excellent treatment of Markov processes pp. 449ff. Discusses Z-transforms, D transforms in their context.
- Kemeny, John G.; Mirkil, Hazleton; Snell, J. Laurie; Thompson, Gerald L. (1959). Finite Mathematical Structures (1.1 yayıncı = Prentice-Hall, Inc. bas.). Englewood Cliffs, N.J. Library of Congress Card Catalog Number 59-12841. Classical text. cf Chapter 6 Finite Markov Chains pp. 384ff.
Dış bağlantılar
- (pdf) Markov Chains chapter in American Mathematical Society's introductory probability book 22 Mayıs 2008 tarihinde Wayback Machine sitesinde .
- Generates random parodies in the style of another body of text using a Markov chain algorithm 4 Haziran 2008 tarihinde Wayback Machine sitesinde .
- A generator that uses Markov Chains to create random words 9 Mayıs 2008 tarihinde Wayback Machine sitesinde .
- Markov zinciri, PlanetMath.org.
- (About generating random text using a Markov chain.)
- The World's Largest Matrix Computation 9 Mayıs 2008 tarihinde Wayback Machine sitesinde . (Google's PageRank as the stationary distribution of a random walk through the Web.)
- Dissociated Press20 Mayıs 2012 tarihinde Wayback Machine sitesinde . in Emacs approximates a Markov process
- nth order Markov Chain implementation in Ruby 13 Mayıs 2008 tarihinde Wayback Machine sitesinde .
- Baseball Run Modeler using Markov Chains 27 Mart 2008 tarihinde Wayback Machine sitesinde .
- Theory of Markov chains in baseball9 Aralık 2007 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Ekim 2021 Matematikte Markov Zinciri Andrey Markov un adina atfen sahip bir stokastik surectir Markov ozelligine sahip olmak mevcut durum verildiginde gelecek durumlarin gecmis durumlardan bagimsiz olmasi anlamina gelir Bir baska deyisle mevcut durumun aciklamasi surecin gelecekteki evrimini etkileyebilecek tum bilgiyi kapsar Gelecek durumlara belirli bir sekilde degil olasiliksal bir surecle ulasilacaktir Her bir anda sistem belirli bir olasilik dagilimina bagli olarak kendi durumunundan baska bir duruma gecebilir yahut ayni durumda kalabilir Durumda olan degisiklikler gecis olarak bilinir ve cesitli durum degismeleriyle iliskili olasiliklar da gecis olasiliklari olarak adlandirilir Markov zincirine bir ornek olur Basit rastgele yuruyus icin durum uzayi bir gosterim ustunde bir grup koseler halindedir Gecis asamalari ise yuruyusun gecmisinde ne olmus olursa olsun cari koseden herhangi bir komsu koseye gitmeyi kapsar Cari koseden herhangi bir komsu koseye gitme olasiligi hep ayni olup birbirine esittir TanimiMarkov zincir tasiyan yani mevcut durum verilmis olursa gecmis ve gelecek durumlarin bagimsiz oldugu ardi ardina gelen X1 X2 X3 ile ifade edilen bir seri rassal degiskendir Matematiksel bicimle Pr Xn 1 x Xn xn X1 x1 Pr Xn 1 x Xn xn displaystyle Pr X n 1 x X n x n ldots X 1 x 1 Pr X n 1 x X n x n Xi in mumkun degerleri S olarak ifade edilen ve zincirin durum uzayi adi verilen olusturur Cok kere Markov zincirleri bir ile tanimlanmaktadir ve bu gosterimde kenar dogrular bir durumdan diger bir duruma gecis olasiliklari ile tanitilmaktadir Cesitlemeleri surekli bir endeksi bulunur Zaman icinde homojen Markov zincirleri zamana gore homojen olan gecis olasiliklari bulunan Markov zincirleridir ve tum n degerleri icin Pr Xn 1 x Xn y Pr Xn x Xn 1 y displaystyle Pr X n 1 x X n y Pr X n x X n 1 y olan sureclerdir m sonlu bir sayi ise bir m dereceli bir Markov zinciri yani m bellekli bir Markov zinciri icin tum n degerleri icin su ifadeler verilebilir Pr Xn xn Xn 1 xn 1 Xn 2 xn 2 X1 x1 displaystyle Pr X n x n X n 1 x n 1 X n 2 x n 2 dots X 1 x 1 Pr Xn xn Xn 1 xn 1 Xn 2 xn 2 Xn m xn m displaystyle Pr X n x n X n 1 x n 1 X n 2 x n 2 dots X n m x n m Klasik olan Xn den yeni bir Yn zincirinin soyle kurulmasi mumkundur Yn siralamali m boyutlu X degerlerinden soyle kurulsun Yn Xn Xn 1 Xn m 1 O zaman Yn durum uzayi Sm olan ve klasik bulunan bir Markov zinciri olur OrnekMarkov zincirlerinin ozellikleriIndirgenebilirlik Donemsellik Tekrarlama Eger i durumdan basladigimiz bilindigi halde i durumuna hicbir zaman donme imkani yaratmayan bir sifira esit olamayan olasilik bulunuyorsa i durumu gecis durum olarak nitelendirilir Daha matematik bicimle ve notasyonla bir rassal degisken olan Ti i durumuna ilk geri donus zamani vurma zamani olsun yani Ti inf n Xn i X0 i displaystyle T i inf n X n i X 0 i Bu halde i durumu gecisli olmasi icin ancak ve ancak Pr Ti gt 0 displaystyle Pr T i infty gt 0 olmalidir Eger bir durum i gecisli degilse yani 1 olasilikla bir sonlu olan vurma zamanina sahipse o halde i durumu yinelenen veya israrli durum olarak adlandirilir Vurma zamani sonlu olmakla beraber bir sonlu beklenen degeri bulunmasi gerekmez Mi beklenen geri donus zamani yani Mi E Ti displaystyle M i E T i olsun O halde eger Mi sonlu ise i durumu da pozitif yinelenen olur aksi halde i durumu sifir yinelenen olacaktir bu durumlara ayni sirayla sifir olmayan israrli veya sifir israrli durum adlari da verilir Bir durumun yinelenen olmasi n 0 pii n displaystyle sum n 0 infty p ii n infty ifadesi gercekse ortaya cikacagi ispatlanamistir Eger durum i yi girdikten sonra hicbir zaman o durumdan cikmak mumkun degilse i durumu yutan durum olarak adlandirilir Bu halde i durumu yutan durum olmasi icin su kosulu saglamasi gerekir pii 1 displaystyle p ii 1 and pij 0 displaystyle p ij 0 for i j displaystyle i not j Ergodiklik P gecis matrisinde tum durumlar birbirleri arasinda gecis saglayabiliyorsa bu zincire ergodik markov zinciri denir 0 1 0 00 0 1 00 0 0 11 0 0 0 ustteki P matrisi ergodik bir markov zinciridir 0 1 0 00 0 1 00 1 0 01 0 0 0 ustteki P matrisi ise ergodik bir markov zinciri degildir Sebebi ise 4 duruma hicbir sekilde varilamamaktadir Sonlu durum uzayinda Markov zincirleriTersinebilir Markov zincirleriBernoulli semasiGenel durum uzayinda Markov zincirleriUygulamalarFizik Sinama Kuyruk kurami Internet uygulamalari Google in kullandigi internet sayfalarinin PageRank i Markov zinciri ile tanimlanmaktadir Markov zincirinde duragan dagilimda tum bilinen internet sayfalari arasindan i displaystyle i sayfasinda bulunma olasiligidir Eger N displaystyle N bilinen internet sayfalari ise ve i displaystyle i sayfasi ki displaystyle ki baglantisina sahip ise o zaman baglantili oldugu tum sayfalar icin 1 qki qN displaystyle frac 1 q ki frac q N ve baglantisi olmadigi tum sayfalar icin qN displaystyle frac q N gecis olasiligina sahiptir q displaystyle q parametresi yaklasik 0 15 olarak alinmistir Markov modelleri ayni zamanda kullanicilarin internet gezinti davranislarini analiz etmek icin de kullanilmistir Bir kullanicinin bir internet sayfasindan web baglantisi ile gecisi birincil ya da ikincil Markov modelleri ile modellenebilir ve gelecekteki hareketleri ongormede ve dolayisiyla internet sayfasini kullanici icin kisisellestirme de kullanilabilir Istatistik Iktisat Matematiksel biyoloji Muzik Beyzbol Markov parodi ureticileriTarihceAyrica bakinizMarkov karar sureciKaynakca ABD patent 6 285 999 A A Markov Rasprostranenie zakona bol shih chisel na velichiny zavisyaschie drug ot druga Izvestiya Fiziko matematicheskogo obschestva pri Kazanskom universitete 2 ya seriya tom 15 pp 135 156 1906 A A Markov Extension of the limit theorems of probability theory to a sum of variables connected in a chain Yeni basim Appendiks B R Howard Dynamic Probabilistic Systems volume 1 Markov Chains John Wiley and Sons 1971 Classical Text in Translation A A Markov An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains trans David Link Science in Context 19 4 2006 591 600 Online http journals cambridge org production action cjoGetFulltext fulltextid 637500 Leo Breiman Probability Original edition published by Addison Wesley 1968 reprinted by Society for Industrial and Applied Mathematics 1992 ISBN 0 89871 296 3 See Chapter 7 J L Doob Stochastic Processes New York John Wiley and Sons 1953 ISBN 0 471 52369 0 S P Meyn and R L Tweedie Markov Chains and Stochastic Stability London Springer Verlag 1993 ISBN 0 387 19832 6 online Second edition to appear Cambridge University Press 2009 S P Meyn Control Techniques for Complex Networks Cambridge University Press 2007 ISBN 9780521884419 Appendix contains abridged Meyn amp Tweedie online Booth Taylor L 1967 Sequential Machines and Automata Theory 1 1 yayinci John Wiley and Sons Inc bas New York Library of Congress Card Catalog Number 67 25924 Extensive wide ranging book meant for specialists written for both theoretical computer scientists as well as electrical engineers With detailed explanations of state minimization techniques FSMs Turing machines Markov processes and undecidability Excellent treatment of Markov processes pp 449ff Discusses Z transforms D transforms in their context Kemeny John G Mirkil Hazleton Snell J Laurie Thompson Gerald L 1959 Finite Mathematical Structures 1 1 yayinci Prentice Hall Inc bas Englewood Cliffs N J Library of Congress Card Catalog Number 59 12841 Classical text cf Chapter 6 Finite Markov Chains pp 384ff Dis baglantilar pdf Markov Chains chapter in American Mathematical Society s introductory probability book 22 Mayis 2008 tarihinde Wayback Machine sitesinde Generates random parodies in the style of another body of text using a Markov chain algorithm 4 Haziran 2008 tarihinde Wayback Machine sitesinde A generator that uses Markov Chains to create random words 9 Mayis 2008 tarihinde Wayback Machine sitesinde Markov zinciri PlanetMath org About generating random text using a Markov chain The World s Largest Matrix Computation 9 Mayis 2008 tarihinde Wayback Machine sitesinde Google s PageRank as the stationary distribution of a random walk through the Web Dissociated Press20 Mayis 2012 tarihinde Wayback Machine sitesinde in Emacs approximates a Markov process nth order Markov Chain implementation in Ruby 13 Mayis 2008 tarihinde Wayback Machine sitesinde Baseball Run Modeler using Markov Chains 27 Mart 2008 tarihinde Wayback Machine sitesinde Theory of Markov chains in baseball9 Aralik 2007 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State