Merkezi limit teoremi büyük bir sayıda olan bağımsız ve aynı dağılım gösteren rassal değişkenlerin (eğer sonlu varyans değerleri bulunuyorsa) aritmetik ortalamasının, yaklaşık olarak normal dağılım (yani Gauss dağılımı) göstereceğini ifade eden bir teoremdir. Matematiksel bir ifadeyle, bir merkezi limit teoremi olasılık kuramı içinde bulunan bir sonucu setidir. Bunların hepsi, birçok bağımsız aynı dağılım gösteren rassal değişkenlerin herhangi bir toplam değerinin limitte belirli bir "çekim gücü gösteren dağılıma" göre dağılım gösterme eğiliminde olduğu gerçeğini önerir.
Pratik gerçekte birçok anakütle, sonlu varyans gösteren dağılımlar ortaya çıkardıkları için, bu teorem normal olasılık dağılımının önemini açığa çıkartır.
Bu teoreminin kapsamını genişletip sonuçlarını genelleştiren eklere göre (, , durumu ve durumu) sonlu varyans gösterme için mutlaka aynı dağılım gerekmemektedir.
Tarihçe
Tijms'in yazdığına göre:
| “ | Merkezi limit teoreminin tarihi gelişmesi çok enterasandır. Bu teoremin ilk şekli Fransız matematikçi Abraham de Moivre tarafından 1733'te yayınlanarak gayet dikkati çeken bir yazıda bulunmakta ve bu yazıda bir yansız madeni paranın yazı-tura atış sonuçların da kaç defa yazı gelme sayısının dağılımının bir normal dağılım ile yaklaşık olarak açıklanabileceğini ortaya çıkartmıştır. Bu gelişme zamanı için çok zor görünüp neredeyse unutulmuştur. Bu unutulmuş konu tanınmış Fransız matematikçisi Pierre-Simon Laplace'ın 1812'de yayınladığı çok tanınmış eseri Thoerie Analytique des Probabilites (Olasılıklar İçin Analitik Kuram)'da yeniden ortaya çıkarılmıştır; Laplace, De Moivre'in buluşunu daha da geliştirerek binom dağılımlarının yaklaşık olarak normal dağılım ile ifade edilip hesaplanabileceği sonucunu ortaya atmıştır. Ancak De Moivre gibi Laplace gelişmeleri de yaşadığı çağda çok az dikkati çekmiştir. Sonunda 19. yüzyılın içinde merkezi limit teoreminin önemi anlaşılmış ve 1901 Rus matematikçisi Aleksandr Lyapunov bu teoremi genel bir şekilde açıklamış ve matematik olarak nasıl ortaya çıktığını çok kesin bir şekilde ispatlamıştır. Bugün merkezi limit teoremi olasılık kuramının en önemli ögesi, gayriresmî kralı, olduğu kabul edilmektedir." | „ |
Klasik merkezi limit teoremi
Merkezi limit teoremi olasılık kuramı için ikinci temel teorem olarak kabul edilmektedir. (Birinci temel teorem büyük sayılar yasasıdır.) 




Rassal değişkenlerin 
ve
bir standart normal 
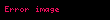
Bu göre limitte 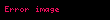

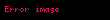
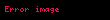
Bu demektir ki; eğer 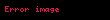
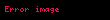

veya,
olur. Burada
örneklem ortalaması olur.
Yillarca, büyük örneklem hacmi pratik olarak 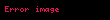

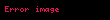
Merkezi limit teoreminin ispatı
Olasılık kuramı ve istatistik bilimleri için temel önem taşıyan merkezi limit teoremi'nin ispatı karakteristik fonksiyonu kullanarak kolayca yapılabilir. Bu ispat zayıf büyük sayılar yasasını ispat etmek için kullanılan yönteme çok benzemektedir.
Sıfır ortalamaya ve birim varyansa sahip herhangi bir rassal değişken 
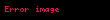
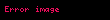

Burada 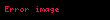

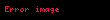
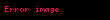
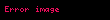
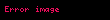

olur. Karakteristik fonksiyonun basit niteliklerine dayanarak, 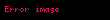
olduğu çıkartılır. Bu limit ise açıkça 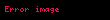
Limite yakınsama
Eğer üçüncü merkezsel moment E((X1 − μ)3) bulunuyorsa ve sonlu ise, yukarıda açıklanan yakınsalaşma ile yakınsalaşma hızı asgari 1/n½ olur. Yakınsalaşma normali monotoniktir yani 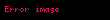
Bir dağılımın toplama ile "düzgünleştirilmesi" için grafikler orijinal olasılık dağılım fonksiyonu ve diğer üç (dağılım fonksiyonların konvolusyonu ile elde edilen) toplama için şu grafiklerde görülür:




Merkezi limit teoreminin bir grafiksel temsili bir anakütlenin rassal ortalamalarının grafiği ile gösterilebilir. Bir An alalım ve bu bir rassal örneklem için örneklem ortalaması ve her bir örneklemden tek bir rassal değişken de Xn olsun:
An = (X1 + ... + Xn) / n
1den verilen bir örneklem hacmine kadar An ifadesini bulalım:
A1 = (X1) / 1
A2 = (X1 + X2)/ 2
A3 = (X1 + X2 + X3)/3
Merkezi limit teoremi için ortalamaları örneklem hacmi 90a kadar yani 30 nokta olarak gösterilmesi gerekir. Eğer An
Zn = (An − μ) / (σ / n½)
kullanılarak standartize edilirse, yukarıda verilen Zn değişkeninin aynısı ortaya çıkar ve bu bir standart normal dağılımına yakınsanır.
Merkezi Limit teoremi sonlu sayıda gözlemler için bir tahmin olarak kullanılması gerek bu sayılar normal dağılımın zirvesi etrafında toplanırsa iyi sonucdur; dağılımın kuyruklarında olan gözlemler için bu tahminin yeterince doğru olması için çok sayıda gözlem elde edilmesi gerekir.
Merkezi Limit Teoremi özellikle bağımsız ve aynen dağılım gösteren için uygulanır. Ayrık rassal değişken için bir toplama ile elde edilen değerde bir ayrık rassal değişkendir ve böylece bir seri ayrık rassal değişken için tek tek yığmalı olasılık dağılım fonksiyonu bir sürekli değişken için bir yığmalı olasılık dağılım fonksiyonua (yani normal dağılıma) yakınsalaşır.
Bu demektir ki eğer n sayıda bağımsız ve özdeş ayrık değişkenlerin toplamının gerçekleşmelerinin bir histogramını kurarsak, histogramı şekillendiren dikdörtgenlerin yukarı yüzlerinin merkezlerini birleştiren eğri, n' 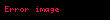
Büyük sayılar yasasına ilişkisi
Hem büyük sayılar yasası hem de Merkezi Limit Teoremi daha genel bir problemin kısmı çözümleri olmaları çok olasıdır. Bu genel problem şöyle ifade edilebilir: "Eğer n sonsuz değere yakınsamaktaysa Sn ifadesinin yakınsama davranışı ne olur?". Matematik analizde bu çeşit sorulara yaklaşmak için en popüler matematik araç konumuna dayanır.
f(n) fonsksiyonunun asimtotik genişletilmesin şu olduğunu kabul edelim:
Bu ifadenin her iki tarafını da 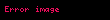
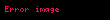
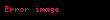
Formel olmadan bu şöyle açıklanabilir: "fonksiyon ile onu yakalsık olarak ifadenin arasındaki fark 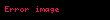
Sn ifadesinin klasik olasılık teoride incelenmesinde de aynı usulde açıklama yapılmaktadır. Belirli düzenleme koşulları altında, eğer 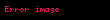
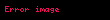
hem de Merkezi Limit Teoremi yani
şu formel olmayan ifadenin ilk iki sabitlerinin değerlerini verirler:
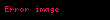
Eğer X1, X2, X3, ... bağımsız ve özdeş ifadeler ise ve belli bir 
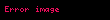
olur ve böylece 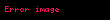
Teoremin alternatif şekillerde ifade edilmesi
Yoğunluk fonksiyonları
Pozitif rassal değişkenlerinin çarpımları
Lyapunov koşulu
Main: .
Lindeberg koşulu
Uygulamalar ve örneğinler
Sinyal işleme
Ayrıca bakınız
Notlar
- ^ Henk Tijms, Understanding Probability: Chance Rules in Everyday Life 6 Mayıs 2021 tarihinde Wayback Machine sitesinde ., (s. 169), Cambridge: Cambridge University Press, 2004.
- ^ Merkezi limit teoreminin gelişmesinin çok geniş ayrıntıları ile açıklanması, özellikle Laplace'in teoreminin temelleri hakkındaki çalışmaları ve Cauchy, ve 'un katkıları Hald tarafından incelemektedir. Bakınız: Andreas Hald, History of Mathematical Statistics from 1750 to 1930 18 Temmuz 2011 tarihinde Wayback Machine sitesinde ., Ch.17.
- ^ Bakın "Identification of Misconceptions in the Central Limit Theorem and Related Concepts and Evaluation of Computer Media as a Remedial Tool" Yu, Chong Ho ve Dr. John T. Behrens, Arizona State University ve Spencer Anthony, Univ. of Oklahoma: "American Educational Research Association" Yıllık Toplantısı için makale. Sunma tarihi: 19 Nisan, 1995 ve revizyon: 12 Şubat, 1997, CWisdom-rtf 5 Aralık 2008 tarihinde Wayback Machine sitesinde .(Erişme:25.10.2007).
- ^ Marasinghe, M., Meeker, W., Cook, D. & Shin, T.S.(1994 August), "Using graphics and simulation to teach statistical concepts", American Statistician Association'un, Toronto, Kanada 1994 yılı için yıllık konferansına sunulan bir makale.
Kaynakça
- Henk Tijms (2004), Understanding Probability: Chance Rules in Everyday Life 6 Mayıs 2021 tarihinde Wayback Machine sitesinde ., Cambridge: Cambridge University Press.
- S. Artstein, K. Ball, F. Barthe ve A. Naor, (2004) "Solution of Shannon's Problem on the Monotonicity of Entropy", Journal of the American Mathematical Society C.17, say. 975-982 .
- S.N.Bernstein (1945), On the work of P.L.Chebyshev in Probability Theory, Nauchnoe Nasledie P.L.Chebysheva. Vypusk Pervyi: Matematika. (Rusca) [The Scientific Legacy of P. L. Chebyshev. First Part: Mathematics] Editor S. N. Bernstein.] Academiya Nauk SSSR, Moscow-Leningrad, 174 say.
- G. Rempala ve J. Wesolowski, (2002) "Asymptotics of products of sums and U-statistics", Electronic Communications in Probability, C. 7, say. 47-54.
Dış bağlantılar
- Çizimlerle Merkezi Limit Teoremi 5 Nisan 2011 tarihinde Wayback Machine sitesinde .
- Merkezi Limit Teoremi için örnekler13 Eylül 2008 tarihinde Wayback Machine sitesinde .
- Merkezi Limit Teoremi 27 Nisan 2008 tarihinde Wayback Machine sitesinde . Değişik parametre değerleri için deneysel etkileşimli simülasyon.
- CLT in NetLogo (Connected Probability - ProbLab)22 Mart 2006 tarihinde Wayback Machine sitesinde . Değiştirilebilen parametre değerleri ile etkileşimli simülasyon
- Genel Merkezi Limit Teoremi Aktivitesi 29 Nisan 2008 tarihinde Wayback Machine sitesinde . & corresponding (Select the Sampling Distribution CLT Experiment from the drop-down list of SOCR Experiments 29 Nisan 2008 tarihinde Wayback Machine sitesinde .)
- Generate sampling distributions in Excel 17 Mayıs 2008 tarihinde Wayback Machine sitesinde . Specify arbitrary population, , and sample statistic.
- [1] 30 Mart 2007 tarihinde Wayback Machine sitesinde . Diğer bir ispat.
- CAUSEweb.org 5 Mart 2016 tarihinde Wayback Machine sitesinde . Merkezi Limit Teoremi dahil çeşitli istatistik yöntemi öğretmesi için çeşitli öğretme kaynakları bulunan bir web sitesi
- Merkezi Limit Teoremi 5 Mayıs 2008 tarihinde Wayback Machine sitesinde . Chris Boucher, .
- Eric W. Weisstein, Central Limit Theorem (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Merkezi limit teoremi buyuk bir sayida olan bagimsiz ve ayni dagilim gosteren rassal degiskenlerin eger sonlu varyans degerleri bulunuyorsa aritmetik ortalamasinin yaklasik olarak normal dagilim yani Gauss dagilimi gosterecegini ifade eden bir teoremdir Matematiksel bir ifadeyle bir merkezi limit teoremi olasilik kurami icinde bulunan bir sonucu setidir Bunlarin hepsi bircok bagimsiz ayni dagilim gosteren rassal degiskenlerin herhangi bir toplam degerinin limitte belirli bir cekim gucu gosteren dagilima gore dagilim gosterme egiliminde oldugu gercegini onerir Pratik gercekte bircok anakutle sonlu varyans gosteren dagilimlar ortaya cikardiklari icin bu teorem normal olasilik dagiliminin onemini aciga cikartir Bu teoreminin kapsamini genisletip sonuclarini genellestiren eklere gore durumu ve durumu sonlu varyans gosterme icin mutlaka ayni dagilim gerekmemektedir TarihceTijms in yazdigina gore Merkezi limit teoreminin tarihi gelismesi cok enterasandir Bu teoremin ilk sekli Fransiz matematikci Abraham de Moivre tarafindan 1733 te yayinlanarak gayet dikkati ceken bir yazida bulunmakta ve bu yazida bir yansiz madeni paranin yazi tura atis sonuclarin da kac defa yazi gelme sayisinin dagiliminin bir normal dagilim ile yaklasik olarak aciklanabilecegini ortaya cikartmistir Bu gelisme zamani icin cok zor gorunup neredeyse unutulmustur Bu unutulmus konu taninmis Fransiz matematikcisi Pierre Simon Laplace in 1812 de yayinladigi cok taninmis eseri Thoerie Analytique des Probabilites Olasiliklar Icin Analitik Kuram da yeniden ortaya cikarilmistir Laplace De Moivre in bulusunu daha da gelistirerek binom dagilimlarinin yaklasik olarak normal dagilim ile ifade edilip hesaplanabilecegi sonucunu ortaya atmistir Ancak De Moivre gibi Laplace gelismeleri de yasadigi cagda cok az dikkati cekmistir Sonunda 19 yuzyilin icinde merkezi limit teoreminin onemi anlasilmis ve 1901 Rus matematikcisi Aleksandr Lyapunov bu teoremi genel bir sekilde aciklamis ve matematik olarak nasil ortaya ciktigini cok kesin bir sekilde ispatlamistir Bugun merkezi limit teoremi olasilik kuraminin en onemli ogesi gayriresmi krali oldugu kabul edilmektedir Klasik merkezi limit teoremiMerkezi limit teoremi olasilik kurami icin ikinci temel teorem olarak kabul edilmektedir Birinci temel teorem buyuk sayilar yasasidir X1 X2 Xn displaystyle X 1 X 2 X n n displaystyle n tane bagimsiz ve ayni sekilde sonlu sayida ve m displaystyle mu ortalamasiyla ve s2 displaystyle sigma 2 varyansiyla dagilim gosteren rassal degiskenler olsun Merkezi limit teoremine gore degisken sayisi n displaystyle n artarak sonsuza yaklastikca orijinal dagilim her ne sekilde olursa olsun ortalamasi m displaystyle mu ve varyansi s2 displaystyle sigma 2 olan bir normal dagilima yakinsama gosterir Rassal degiskenlerin Sn displaystyle S n ile ifade edilen toplami soyle verilsin Sn X1 Xn displaystyle S n X 1 X n ve Zn Sn nmsn displaystyle Z n frac S n n mu sigma sqrt n bir standart normal m displaystyle mu ortalamali ve sn displaystyle sigma sqrt n varyansli standart normal dagilim olsun Bu gore limitte n displaystyle n rightarrow infty Sn displaystyle S n nin dagilimi olan Zn displaystyle Z n dagilimi N 0 1 displaystyle N 0 1 standart normal dagilimina yaklasir Bu demektir ki eger F z displaystyle Phi z N 0 1 displaystyle N 0 1 dagiliminin yigmali dagilim fonksiyonu ise o halde her z displaystyle z reel sayisi icin limn P Zn z F z displaystyle lim n to infty mbox P Z n leq z Phi z veya limn P X n ms n z F z displaystyle lim n rightarrow infty mbox P left frac overline X n mu sigma sqrt n leq z right Phi z olur Burada X n Snn X1 Xn n displaystyle overline X n S n over n X 1 cdots X n over n orneklem ortalamasi olur Yillarca buyuk orneklem hacmi pratik olarak n gt 29 displaystyle n gt 29 olarak kabul edilmekteydi Fakat 1990 li yillarda yapilan arastirmalar ortaya cikarmistir ki bu pratik kural her zaman gecerli degildir Anakutle ne kadar cok carpiklik gosterirse gereken buyuk orneklem hacminin gittikce daha buyuk olmasi gerekmektedir Bu sekilde carpiklik gosteren anakutleler pratikte cok nadir bulunabilirler Bu pratik kurala dayanan ve cikarimsal istatistik icin kullanilan Student in t dagilimi tablolarina ancak n 30 displaystyle n 30 verilmektedir ama simulasyon ve bilgisayar animasyonu ile gosterilmistir ki Student in t dagilimi tablolari icin secilen en yuksek orneklem hacmi olan n gt 29 displaystyle n gt 29 yeterli buyuklukte degildir Merkezi limit teoreminin ispati Olasilik kurami ve istatistik bilimleri icin temel onem tasiyan merkezi limit teoremi nin ispati karakteristik fonksiyonu kullanarak kolayca yapilabilir Bu ispat zayif buyuk sayilar yasasini ispat etmek icin kullanilan yonteme cok benzemektedir Sifir ortalamaya ve birim varyansa sahip herhangi bir rassal degisken Y displaystyle Y alalim yani E Y 0 displaystyle E Y 0 var Y 1 displaystyle var Y 1 Taylor teoremi kullanilarak Y displaystyle Y icin karakteristik fonksiyonun su oldugu bilinir fY t 1 t22 o t2 t 0 displaystyle varphi Y t 1 t 2 over 2 o t 2 quad t rightarrow 0 Burada t2 displaystyle t 2 ifadesinden daha hizli sifira yaklasan herhangi bir t2 displaystyle t 2 icin o t2 0 displaystyle o t 2 rightarrow 0 olur Yi displaystyle Y i ifadesini Xi textstyle X i standardize edilmis degeri yani Xi m s textstyle X i mu sigma olarak koyalim Bu halde X1 X2 Xn displaystyle X 1 X 2 X n gozlem noktalarinin standardize edilmis ortalamasi Zn nX n nmsn i 1nYin displaystyle Z n frac n overline X n n mu sigma sqrt n sum i 1 n Y i over sqrt n olur Karakteristik fonksiyonun basit niteliklerine dayanarak Zn displaystyle Z n icin karakteristik fonksiyonun fY tn n 1 t22n o t2n n e t2 2 n displaystyle left varphi Y left t over sqrt n right right n left 1 t 2 over 2n o left t 2 over n right right n rightarrow e t 2 2 quad n rightarrow infty oldugu cikartilir Bu limit ise acikca N 0 1 displaystyle N 0 1 standart normal dagilimi icin karakteristik fonksiyondur ve merkezi limit teoremi karakteristik fonksiyonlarin yakinsamasinin dagilimin yakinsamasina esit oldugunu bildiren kullanarak ispat edilmis olur Limite yakinsama Eger ucuncu merkezsel moment E X1 m 3 bulunuyorsa ve sonlu ise yukarida aciklanan yakinsalasma ile yakinsalasma hizi asgari 1 n olur Yakinsalasma normali monotoniktir yani Zn displaystyle Z n nin bir normal dagilim entropisine monotonik olarak yakinsalasir Bir dagilimin toplama ile duzgunlestirilmesi icin grafikler orijinal olasilik dagilim fonksiyonu ve diger uc dagilim fonksiyonlarin konvolusyonu ile elde edilen toplama icin su grafiklerde gorulur Merkezi limit teoreminin bir grafiksel temsili bir anakutlenin rassal ortalamalarinin grafigi ile gosterilebilir Bir An alalim ve bu bir rassal orneklem icin orneklem ortalamasi ve her bir orneklemden tek bir rassal degisken de Xn olsun An X1 Xn n 1den verilen bir orneklem hacmine kadar An ifadesini bulalim A1 X1 1 A2 X1 X2 2 A3 X1 X2 X3 3 Merkezi limit teoremi icin ortalamalari orneklem hacmi 90a kadar yani 30 nokta olarak gosterilmesi gerekir Eger An Zn An m s n kullanilarak standartize edilirse yukarida verilen Zn degiskeninin aynisi ortaya cikar ve bu bir standart normal dagilimina yakinsanir Merkezi Limit teoremi sonlu sayida gozlemler icin bir tahmin olarak kullanilmasi gerek bu sayilar normal dagilimin zirvesi etrafinda toplanirsa iyi sonucdur dagilimin kuyruklarinda olan gozlemler icin bu tahminin yeterince dogru olmasi icin cok sayida gozlem elde edilmesi gerekir Merkezi Limit Teoremi ozellikle bagimsiz ve aynen dagilim gosteren icin uygulanir Ayrik rassal degisken icin bir toplama ile elde edilen degerde bir ayrik rassal degiskendir ve boylece bir seri ayrik rassal degisken icin tek tek yigmali olasilik dagilim fonksiyonu bir surekli degisken icin bir yigmali olasilik dagilim fonksiyonua yani normal dagilima yakinsalasir Bu demektir ki eger n sayida bagimsiz ve ozdes ayrik degiskenlerin toplaminin gerceklesmelerinin bir histogramini kurarsak histogrami sekillendiren dikdortgenlerin yukari yuzlerinin merkezlerini birlestiren egri n displaystyle infty degerine yakinsalastikca bir Gauss tipi can egrisine gittikce benzemeye baslar Basit sadece iki deger alan bir ayrik degiskeni iceren binom dagilimi gosterdigi simule edilen bir halde bile bu merkezi limit teoremi uygulandigi gorulebilir Buyuk sayilar yasasina iliskisi Hem buyuk sayilar yasasi hem de Merkezi Limit Teoremi daha genel bir problemin kismi cozumleri olmalari cok olasidir Bu genel problem soyle ifade edilebilir Eger n sonsuz degere yakinsamaktaysa Sn ifadesinin yakinsama davranisi ne olur Matematik analizde bu cesit sorulara yaklasmak icin en populer matematik arac konumuna dayanir f n fonsksiyonunun asimtotik genisletilmesin su oldugunu kabul edelim f n a1f1 n a2f2 n O f3 n n displaystyle f n a 1 varphi 1 n a 2 varphi 2 n O varphi 3 n n rightarrow infty Bu ifadenin her iki tarafini da f1 n displaystyle varphi 1 n ile bolersek ve limit alirsak en f n displaystyle f n fonksiyonunun en bastaki terimin degisme haddini temsil eden genisletilmenin en yuksek siradaki katsayisi olan a1 displaystyle a 1 ifadesini uretiriz limn f n f1 n a1 displaystyle lim n to infty frac f n varphi 1 n a 1 Formel olmadan bu soyle aciklanabilir fonksiyon ile onu yakalsik olarak ifadenin arasindaki fark a2f2 n displaystyle a 2 varphi 2 n haddinde buyur Bu kavramin ana sonucu soyledir fonksiyonu uygun bir yaklasik veren normalize eden fonksiyonlar ile bolersek ve bu sonucun limitteki davranisina bakarsak bu netice orijinal fonksiyonun limitteki davranisi hakkinda epeyce cok aciklama yapar Sn ifadesinin klasik olasilik teoride incelenmesinde de ayni usulde aciklama yapilmaktadir Belirli duzenleme kosullari altinda eger 3 displaystyle xi ifadesi N 0 s2 displaystyle N 0 sigma 2 olarak dagilim gosterirse hem Buyuk Sayilar Yasasi yani Snn m displaystyle frac S n n rightarrow mu hem de Merkezi Limit Teoremi yani Sn nmn 3 displaystyle frac S n n mu sqrt n rightarrow xi su formel olmayan ifadenin ilk iki sabitlerinin degerlerini verirler Sn mn 3n displaystyle S n approx mu n xi sqrt n Eger X1 X2 X3 bagimsiz ve ozdes ifadeler ise ve belli bir 1 b lt 2 displaystyle 1 leq beta lt 2 icin E X1 b lt displaystyle E X 1 beta lt infty ifadesi gecerli ise o zaman Sn nmn1b 0 displaystyle frac S n n mu n frac 1 beta to 0 olur ve boylece n displaystyle sqrt n sifir olmayan limitleyici davranisi temin eden bir normalize etme fonksiyonu hizmetini goren n nin en yuksek ussu olur Takrarlanan logaritma yasasi ise cok ilgi cekici olarak nlog log n displaystyle sqrt n log log n normalize edici fonksiyonun Buyuk Sayilar Yasasi icin n ile Merkezi Limit Teoremi icin n displaystyle sqrt n ifadeleri arasinda oldugunu bildirir ve bu iki teorem ifadesi de bu degerin iki tarafinda bulunan limitleri gosterir demektedir Teoremin alternatif sekillerde ifade edilmesiYogunluk fonksiyonlari Pozitif rassal degiskenlerinin carpimlariLyapunov kosuluMain Lindeberg kosuluUygulamalar ve orneginlerSinyal islemeAyrica bakinizBuyuk sayilar yasasiNotlar Henk Tijms Understanding Probability Chance Rules in Everyday Life 6 Mayis 2021 tarihinde Wayback Machine sitesinde s 169 Cambridge Cambridge University Press 2004 Merkezi limit teoreminin gelismesinin cok genis ayrintilari ile aciklanmasi ozellikle Laplace in teoreminin temelleri hakkindaki calismalari ve Cauchy ve un katkilari Hald tarafindan incelemektedir Bakiniz Andreas Hald History of Mathematical Statistics from 1750 to 1930 18 Temmuz 2011 tarihinde Wayback Machine sitesinde Ch 17 Bakin Identification of Misconceptions in the Central Limit Theorem and Related Concepts and Evaluation of Computer Media as a Remedial Tool Yu Chong Ho ve Dr John T Behrens Arizona State University ve Spencer Anthony Univ of Oklahoma American Educational Research Association Yillik Toplantisi icin makale Sunma tarihi 19 Nisan 1995 ve revizyon 12 Subat 1997 CWisdom rtf 5 Aralik 2008 tarihinde Wayback Machine sitesinde Erisme 25 10 2007 Marasinghe M Meeker W Cook D amp Shin T S 1994 August Using graphics and simulation to teach statistical concepts American Statistician Association un Toronto Kanada 1994 yili icin yillik konferansina sunulan bir makale KaynakcaHenk Tijms 2004 Understanding Probability Chance Rules in Everyday Life 6 Mayis 2021 tarihinde Wayback Machine sitesinde Cambridge Cambridge University Press S Artstein K Ball F Barthe ve A Naor 2004 Solution of Shannon s Problem on the Monotonicity of Entropy Journal of the American Mathematical Society C 17 say 975 982 S N Bernstein 1945 On the work of P L Chebyshev in Probability Theory Nauchnoe Nasledie P L Chebysheva Vypusk Pervyi Matematika Rusca The Scientific Legacy of P L Chebyshev First Part Mathematics Editor S N Bernstein Academiya Nauk SSSR Moscow Leningrad 174 say G Rempala ve J Wesolowski 2002 Asymptotics of products of sums and U statistics Electronic Communications in Probability C 7 say 47 54 Dis baglantilarCizimlerle Merkezi Limit Teoremi 5 Nisan 2011 tarihinde Wayback Machine sitesinde Merkezi Limit Teoremi icin ornekler13 Eylul 2008 tarihinde Wayback Machine sitesinde Merkezi Limit Teoremi 27 Nisan 2008 tarihinde Wayback Machine sitesinde Degisik parametre degerleri icin deneysel etkilesimli simulasyon CLT in NetLogo Connected Probability ProbLab 22 Mart 2006 tarihinde Wayback Machine sitesinde Degistirilebilen parametre degerleri ile etkilesimli simulasyon Genel Merkezi Limit Teoremi Aktivitesi 29 Nisan 2008 tarihinde Wayback Machine sitesinde amp corresponding Select the Sampling Distribution CLT Experiment from the drop down list of SOCR Experiments 29 Nisan 2008 tarihinde Wayback Machine sitesinde Generate sampling distributions in Excel 17 Mayis 2008 tarihinde Wayback Machine sitesinde Specify arbitrary population and sample statistic 1 30 Mart 2007 tarihinde Wayback Machine sitesinde Diger bir ispat CAUSEweb org 5 Mart 2016 tarihinde Wayback Machine sitesinde Merkezi Limit Teoremi dahil cesitli istatistik yontemi ogretmesi icin cesitli ogretme kaynaklari bulunan bir web sitesi Merkezi Limit Teoremi 5 Mayis 2008 tarihinde Wayback Machine sitesinde Chris Boucher Eric W Weisstein Central Limit Theorem MathWorld
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans