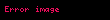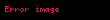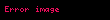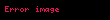Moment (fizik)

Fizikte moment, fiziksel niceliğin mesafe ile bileşimidir. Momentler, genellikle sabit bir referans noktasına ya da eksene göre tanımlanırlar, ilgili referans noktasından ya da ekseninden belirli bir mesafede ölçülen fiziksel nicelikleri ele alırlar. Mesela bir kuvvetin momenti, o kuvvetin kendisinin ve bir eksenden uzaklığının çarpımıdır ve ilgili eksenin etrafında dönmeye sebep olur. Prensip olarak herhangi bir fiziksel nicelik, moment oluşturmak üzere bir mesafe ile bileşebilir. Sıkça kullanılan nicelikler içinde kuvvetler, kütleler ve elektrik yük dağılımları bulunmaktadır.

Detaylı anlatımı

En basit ve temel biçimiyle moment, belirli bir noktaya olan mesafenin belirli bir üst alma işlemine tabii tutulmasından sonra kuvvet, yük gibi fiziksel bir nicelikle çarpımıdır. Bu hâliyle

${\displaystyle \mu _{n}=r^{n}\,Q(r)}$

olur. Burada ${\displaystyle Q}$, fiziksel niceliği göstermektedir – belirli noktaya, nokta yüke ya da nokta kütleye uygulanan kuvvet gibi. Eğer nicelik sadece tek bir noktaya yoğunlaşmamışsa moment niceliğin uzaydaki yoğunluğunun integralidir:

${\displaystyle \mu _{n}=\int r^{n}\,\rho (r)\,dr}$

Burada ${\displaystyle \rho }$ yükü, kütle ya da seçilen herhangi bir niceliğin yoğunluğunun dağılımıdır.

Daha karmaşık biçimler, mesafe ve fiziksel nicelik arasındaki açısal ilişkiyi de dikkate alır, ancak yukarıdaki denklemler bir momentin temel özelliğini, kısacası esas olan ${\displaystyle r^{n}\,\rho (r)}$ terimini veya eşleniğini, ifade etmektedirler.Bu da demektir ki, (her n değeri için) birden çok moment vardır ve moment genellikle,${\displaystyle r}$ mesafesinin ölçüldüğü, referans noktasına bağımlıdır. Gerçi bâzı momentler için (teknik olarak, en düşük sıfır-olmayan moment), bu bağımlılık yok olur ve moment referans noktasında bağımsız hâle gelir.

n'in sahip olduğu her değer farklı momente denk gelmektedir: birinci moment, n=1 'e denk gelmektedir;ikinci moment, n=2 'e denk gelmektedir, vs. Özellikle elektrik yük dağılımları konusunda; sıfırıncı moment'e(n=0), bazen monopol(tek kutuplu) moment denir; birinci moment'e(n=1), bazen dipol(çift kutuplu) moment denir ve ikinci moment'e (n=2), bazen quadrupol(dört kutuplu) moment denir.

Örnekler

• Elektrik dipol momenti yine "birinci moment" türündedir: birbirine zıt iki nokta yükü için ${\displaystyle \mathbf {p} =q\,\mathbf {d} }$ veya ${\displaystyle \rho (\mathbf {r} )}$ yük yoğunluğuna sahip dağıtık bir yük için ${\displaystyle \int \mathbf {r} \,\rho (\mathbf {r} )\,d^{3}r}$ şeklinde ifade edilir.
• Eylemsizlik momenti "ikinci moment" türündedir: bir nokta yükü için ${\displaystyle I=r^{2}m}$,nokta yükü dizisi için ${\displaystyle \sum _{i}r_{i}^{2}m_{i}}$ veya yük dağılımı ${\displaystyle \rho (\mathbf {r} )}$ olan bir nesne için ${\displaystyle \int r^{2}\rho (\mathbf {r} )\,d^{3}r}$ şeklinde ifade edilir.
• Kuvvetin momenti veya tork, "birinci moment" türündedir: ${\displaystyle \mathbf {\tau } =rF}$, veya, daha genel hâliyle ${\displaystyle \mathbf {r} \times \mathbf {F} }$ şeklinde ifade edilir.

Çoklu momentler

Sonlu ve belirli bölge ile sınırlandırılmış bir yoğunluk fonksiyonu üzerinden örneklenecek olursa, o bölgenin dışında 1/r bir küresel harmonikler dizisi olarak ifade edilebilir:

${\displaystyle \Phi (\mathbf {r} )=\int {\frac {\rho (\mathbf {r'} )}{|\mathbf {r} -\mathbf {r'} |}}d^{3}r'=\sum _{l=0}^{\infty }\sum _{m=-l}^{l}\left({\frac {4\pi }{2l+1}}\right)q_{lm}\,{\frac {Y_{lm}(\theta ,\phi )}{r^{l+1}}}}$

${\displaystyle q_{lm}}$ katsayıları 'multipol momentler' olarak bilinirler ve şu biçimi alırlar:

${\displaystyle q_{lm}=\int (r')^{l}\,\rho (\mathbf {r'} )\,Y_{lm}^{*}(\theta ',\phi ')\,d^{3}r'}$

Burada ${\displaystyle \mathbf {r} '}$ küresel koordinatlar olarak ifade edilirken, ${\displaystyle (r',\phi ',\theta ')}$ ise integrasyon değişkenidir. (Note: yukarıdaki denklemlerdeki işlem düzeni Jackson'ın kitabından alınmıştır.)

Burada ${\displaystyle \rho }$ elektrik yük yoğunluğunu ifade ederken, ${\displaystyle q_{lm}}$ ise, bir anlamda, elektrik yükü momentinin : ${\displaystyle q_{00}}$ monopol moment'tir; ${\displaystyle q_{1m}}$ dipol moment'in projeksiyonlarıdır, ${\displaystyle q_{2m}}$ quadrupol moment'in projeksiyonlarıdır, vb.

Çoklu momentlerin uygulamaları

Multipol genişlemesi 1/r skaler potansiyelleri için de geçerlidir, örnekleri ise elektrik potansiyeli ve yerçekimi potansiyeli'dir. Bu potansiyeller için, denklem, ilk birkaç momentin hesaplanması yoluyla; yüklerin(veya kütlelerin) sınırlandırılmış dağıtımı ile üretilmiş olan alanın gücüne yaklaşmak/yakınsamak için kullanılabilir. Yeterince büyük r değeri için, sadece monopol ve dipol momentleri ile kabul edilebilir bir yaklaşık değer elde edilebilir.Daha üst düzeyden moment hesaplanarak daha kesin bir sonuca ulaşılabilir.

Bu yöntem ayrıca ${\displaystyle \rho }$'nun bilinmeyen dağılımının özelliklerini belirlemek için de kullanılabilir. Multipol(çok kutuplu) momentlere ait ölçümler alınabilir ve esas teşkil eden dağılımın özelliklerinin çıkarılmasında kullanılabilir. Bu yöntem moleküller gibi küçük nesnelere de uygulanabilir, ama ayrıca evrenin kendisine de uygulanmıştır, buna örnek olarakyöntemin, WMAP ve deneylerinde Kozmik mikrodalga arka plan ışımasını çözümlemek için kullanılması gösterilebilir.

Diğer momentler

• , bir nesnenin, kayma gerilmesine karşı olan direnci ile ilgili özelliği.
• , bir nesnenin, eğilmeye ve sekmeye karşı olan direnci ile ilgili özelliği.
• , (kiriş,kolon vs.) eğilmesi ile sonuçlanan bir moment'tir.
• Elektrik dipol momenti – İki veya daha fazla yük arasındaki yük farkını ve yönünü ölçen bir dipol moment'tir. Mesela aralarında d mesafesi bulunan –q ve q yükleri arasındaki elektrik dipol momenti şu şekilde belirtilir: ${\displaystyle (\mathbf {p} =q\mathbf {d} )}$
• Eylemsizlik momenti – ${\displaystyle (I=\Sigma mr^{2})}$ Dönme hareketi ile ilgili tartışmalarda kütle ile benzerdir. Nesnenin dönme oranındaki değişimlere karşı nesnenin gösterdiği direncin ölçümüdür.
  • , bir nesnenin, burulmaya(torsiyon) karşı olan direnci ile ilgili özelliği.
• Manyetik moment – ${\displaystyle (\mathbf {\mu } =I\mathbf {A} )}$ manyetik bir kaynağın yönünü ve kuvvetini ölçen bir dipol moment'tir.
• , bir depremin büyüklüğünü ölçmek için kullanılan nicelik.
• Tork: Kuvvetin momenti

Tarihi

Fizikteki moment kavramı, matematik kavramı olan momentler'den türetilmiştir. Momentler prensibi, Arşimet'in keşfetmiş olduğu kaldıraçın çalışma prensibinden türetilmiştir. Arşimet nesneye uygulanan kuvvetinin momentinin, M = rF olduğunu belirtmiştir, burada F uygulanan kuvvet ve r ise uygulanan kuvvetin nesneye olan mesafesidir.

Ancak moment teriminin tarihsel evrimi ve bu terimin matematik, fizik ve mühendislik gibi bilim dallarındaki kullanımnın ne zaman başladığı belirsizdir.

Kaynakça

1. ^ J. D. Jackson, Classical Electrodynamics, 2. baskı, Wiley, New York, (1975). p. 137
2. ^ M.A. Spackman, "Molecular Electric Moments from X-Ray Diffraction Data", Chemical Reviews, 92 (1992), s. 1769
3. ^ Dittrich and Jayatilaka, Reliable Measurements of Dipole Moments from Single-Crystal Diffraction Data and Assessment of an In-Crystal Enhancement, Electron Density and Chemical Bonding II, Theoretical Charge Density Studies, Stalke, D. (Ed), 2012, http://www.springer.com/978-3-642-30807-9
4. ^ Baumann, D., TASI Lectures on Inflation, 2009, ArXiv e-prints, arXiv:0907.5424 8 Aralık 2018 tarihinde Wayback Machine sitesinde .
5. ^ Robertson, D.G.E.; Caldwell, G.E.; Hamill, J.; Kamen, G.; and Whittlesey, S.N. (2004) Research Methods in Biomechanics. Champaign, IL: Human Kinetics Publ., p. 285.

Ayrıca bakınız

• Momentumun momenti – ${\displaystyle (\mathbf {L} =\mathbf {r} \times m\mathbf {v} )}$ çizgisel momentum'un dönme ile ilgili benzeri/eşleniğidir.
• Mekanik denge durumu – bir nesnenin belirli bir noktaya (pivot nokta) göre, saat yönündeki momentlerinin toplamı ile saat yönünün tersine olan momentlerinin toplamı eşit olacak şekilde ilgili nesne dengelendiğinde geçerlidir.