Montgomery Eğrisi Peter L. Montgomery tarafından 1987’de tanımlanmış, klasik farklı bir formudur. Belirli hesaplamalar için ve özellikle farklı kriptografi uygulamalarında kullanılır.
Tanımı


K cismi üzerinde Montgomery egrisi, belirli A, B ∈ K değerleri için ve B(A2 − 4) ≠ 0 eşitsizliği sağlanıyorken, aşağıdaki eşitsizlikle tanımlanır:
Bu eğri genellikle bir K sonlu cismi üzerinde tanımlı olur. (örnek olarak q elemanın oluşturduğu bir sonlu cisim, K = Fq) Bu sonlu cismin karakteristiği 2'den farklı ve A ∈ K ∖ {−2, 2}, B ∈ K ∖ {0}, olması gerektiğine dikkat edelim. Aynı zamanda A ve B için aynı kısıtlamalara sahip rasyoneller üzerinde de düşünülür.
Montgomery Aritmetiği
Bir eliptik eğri üzerinde noktaları arasında, nokta toplama ve nokta ikileme işlemleri gerçekleştirilebilmektedir. Nokta Toplama; 









Bir nokta için bu tür bir temsilin(dönüşümün) bilgi kaybettiğine dikkat edin: gerçekten 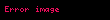




Şimdi, iki nokta dikkate alalım; 

Bu iki noktanın toplamları aşağıdaki şekilde ifade edilir;
bu toplamın koordinatları:
Eğerise bu işlem "nokta ikileme" işlemine dönüşür;
Koordinatları ise aşağıdaki eşitsizliklerle belirlenir;
Yukarıdaki ilk işlemin(toplama işleminin) maliyeti: (3M+2S) (Burada M, tanımlı eliptik eğrideki herhangi iki elemanın çarpımını, S ise tanımlı cisimdeki bir elemanın karesini ifade ediyor)
İkinci işlemin(ikileme) maliyeti : 2M + 2S + 1D, (Burada D herhangi bir elemanın bir 
Algoritma ve Örnek
Montgomery formunda bir eliptik eğrininin bir noktasının 
![image]() varsayıldığı durumda bu implementasyonun maliyeti; 1 + 2 + *1 + 3add + 1*4. (Burada M gerekli çarpma işlemlerini, S ise kare alma işelemlerini, a ise A ile çarpma işlemlerini belirtir.)
varsayıldığı durumda bu implementasyonun maliyeti; 1 + 2 + *1 + 3add + 1*4. (Burada M gerekli çarpma işlemlerini, S ise kare alma işelemlerini, a ise A ile çarpma işlemlerini belirtir.) Örnek
Kabul edelim ki 




Sonuç olarak bulduğumuz nokta; 

Nokta Toplama
afin koordinatlarda Montgomery eğrisi
üzerinde iki nokta olmak üzere,





1) 2 boyutlu afin uzayda, 




2) Doğru ile 


Daha önce gözlemlenebildiği gibi, bu denklem 


şeklinde yazılır.
3) Yukarıda verilen iki özdeş denklemin katsayılarının, özellikle de ikinci mertebeden olanın terimlerinin katsayılarının karşılaştırılmasıyla aşağıdaki denklem elde edilir:
.
Böylelikle,

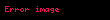


4) 















Öyleyse 

Nokta İkileme








Doğrunun eğimini temsil eden l değeri aşağıdaki gibi verilir:
'ne göre yazılabilir.
Yani 


Bükülmüş Edwards eğrileri ile denkliği
Kabul edelim ki 
Yine kabul edelim ki 
,
![image]()
ve kabul edelim ki 
![image]()
Aşağıdaki teoremi Mongomery eğrileri ile bükülmüş Edwards eğrileri arasındaki gösterir:
Teorem (i) 






:
Dikkat edilirse, iki eğri arasındaki bu denklik her yerde geçerli değildir: gerçekten de 



Weierstrass eğrileri ile denkliği
Tüm eliptik eğriler Weierstrass formunda yazılabilir. Özellikle, Montgomery formundaki eliptik eğriyi ele alalım;
:
aşağıdaki şekilde dönüştürülebilir:
'nin her bir terimini
'e bölüp ve x,y değerlerine,
,
dönüşümü uygulanırsa,
Bir kısa Weierstrass formu elde edebilmek için burada u'yu 
Sonuç olarak:
Dolayısıyla eşleme şöyle verilir:
:
aksine,
:
Montgomery formuna ancak ve ancak 
en az bir
köküne sahip; ve
'de bir ikinci dereceden rezidü.
Bu şartlar sağlandığında, 
:
.
Ayrıca bakınız
Notlar
- ^ (1987). "Speeding the Pollard and Elliptic Curve Methods of Factorization". Mathematics of Computation. 48 (177). ss. 243-264. doi:10.2307/2007888. JSTOR 2007888.
- ^ , Peter Birkner, Marc Joye, Tanja Lange and Christiane Peters (2008). Twisted Edwards Curves (PDF). Springer-Verlag Berlin Heidelberg. ISBN .[]
- ^ Katsuyuki Okeya, Hiroyuki Kurumatani, and Kouichi Sakurai (2000). Elliptic Curves with the Montgomery-Form and Their Cryptographic Applications. Public Key Cryptography (PKC2000). 8 Mart 2018 tarihinde kaynağından . Erişim tarihi: 11 Nisan 2018.
Kaynakça
- (1987). "Speeding the Pollard and Elliptic Curve Methods of Factorization". Mathematics of Computation. 48 (177). ss. 243-264. doi:10.2307/2007888. JSTOR 2007888.
- , Peter Birkner, Marc Joye, Tanja Lange and Christiane Peters (2008). Twisted Edwards Curves (PDF). Springer-Verlag Berlin Heidelberg. ISBN .[]
- Wouter Castryck; Steven Galbraith; Reza Rezaeian Farashahi (2008). (PDF). 29 Temmuz 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 11 Nisan 2018.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Montgomery Egrisi Peter L Montgomery tarafindan 1987 de tanimlanmis klasik farkli bir formudur Belirli hesaplamalar icin ve ozellikle farkli kriptografi uygulamalarinda kullanilir TanimiMontgomery egrisinin denklemi 14y2 x3 2 5x2 x textstyle frac 1 4 y 2 x 3 2 5x 2 x K cismi uzerinde Montgomery egrisi belirli A B K degerleri icin ve B A2 4 0 esitsizligi saglaniyorken asagidaki esitsizlikle tanimlanir MA B By2 x3 Ax2 x displaystyle M A B By 2 x 3 Ax 2 x Bu egri genellikle bir K sonlu cismi uzerinde tanimli olur ornek olarak q elemanin olusturdugu bir sonlu cisim K Fq Bu sonlu cismin karakteristigi 2 den farkli ve A K 2 2 B K 0 olmasi gerektigine dikkat edelim Ayni zamanda A ve B icin ayni kisitlamalara sahip rasyoneller uzerinde de dusunulur Montgomery AritmetigiBir eliptik egri uzerinde noktalari arasinda nokta toplama ve nokta ikileme islemleri gerceklestirilebilmektedir Nokta Toplama P Q displaystyle P Q eliptik egrisi uzerinde tanimli iki nokta olmak uzere R P Q displaystyle R P Q olacak sekilde R displaystyle R noktasi bulmak islemidir Nokta Ikileme ise 2 P P P displaystyle 2 P P P islemidir Kullanilan islemler hakkinda detayli bilgi icin bkz elliptic egri grup kurallari eng the group law P x y displaystyle P x y noktasi Montgomery formundaki By2 x3 Ax2 x displaystyle By 2 x 3 Ax 2 x eliptik egrisi uzerinde bir nokta olmak uzere bu noktanin Montgomery koordinatlari P X Z displaystyle P X Z Burada P X Z displaystyle P X Z x X Z displaystyle x X Z ve Z 0 displaystyle Z neq 0 Bir nokta icin bu tur bir temsilin donusumun bilgi kaybettigine dikkat edin gercekten x y displaystyle x y ve x y displaystyle x y kullaniminda bir ayrim gozetilmez cunku her iki noktanin kullanimi da bize X Z displaystyle X Z sonucunu verecektir Ancak bu gosterim donusum ile bir P X Z displaystyle P X Z noktanin n sayisi ile carpilmasini elde etmek mumkundur n P Xn Zn displaystyle n P X n Z n Simdi iki nokta dikkate alalim Pn n P Xn Zn displaystyle P n n P X n Z n ve Pm m P Xm Zm displaystyle P m m P X m Z m Bu iki noktanin toplamlari asagidaki sekilde ifade edilir Pm n Pm Pn Xm n Zm n displaystyle P m n P m P n X m n Z m n bu toplamin koordinatlari Xm n Zm n Xm Zm Xn Zn Xm Zm Xn Zn 2 displaystyle X m n Z m n X m Z m X n Z n X m Z m X n Z n 2 Zm n Xm n Xm Zm Xn Zn Xm Zm Xn Zn 2 displaystyle Z m n X m n X m Z m X n Z n X m Z m X n Z n 2 Eger m n displaystyle m n ise bu islem nokta ikileme islemine donusur 2 Pn Pn Pn P2n X2n Z2n displaystyle 2 P n P n P n P 2n X 2n Z 2n Koordinatlari ise asagidaki esitsizliklerle belirlenir 4XnZn Xn Zn 2 Xn Zn 2 displaystyle 4X n Z n X n Z n 2 X n Z n 2 X2n Xn Zn 2 Xn Zn 2 displaystyle X 2n X n Z n 2 X n Z n 2 Z2n 4XnZn Xn Zn 2 A 2 4 4XnZn displaystyle Z 2n 4X n Z n X n Z n 2 A 2 4 4X n Z n Yukaridaki ilk islemin toplama isleminin maliyeti 3M 2S Burada M tanimli eliptik egrideki herhangi iki elemanin carpimini S ise tanimli cisimdeki bir elemanin karesini ifade ediyor Ikinci islemin ikileme maliyeti 2M 2S 1D Burada D herhangi bir elemanin bir A 2 4 displaystyle A 2 4 degeri secilebilir Algoritma ve OrnekMontgomery formunda bir eliptik egrininin bir noktasinin P1 X1 Z1 displaystyle P 1 X 1 Z 1 nokta ikilemesi asagidaki algoritma ile gosterilebilir Z1 1 displaystyle Z 1 1 varsayildigi durumda bu implementasyonun maliyeti 1 2 1 3add 1 4 Burada M gerekli carpma islemlerini S ise kare alma iselemlerini a ise A ile carpma islemlerini belirtir XX1 X12 displaystyle XX 1 X 1 2 X3 XX1 1 2 displaystyle X 3 XX 1 1 2 Z3 4X1 XX1 aX1 1 displaystyle Z 3 4X 1 XX 1 aX 1 1 Ornek Kabul edelim ki P1 2 3 displaystyle P 1 2 sqrt 3 noktasi 2y2 x3 x2 x displaystyle 2y 2 x 3 x 2 x egrisi uzerinde bir nokta olsun Koordinatlari X1 Z1 displaystyle X 1 Z 1 x1 X1 Z1 displaystyle x 1 X 1 Z 1 P1 2 1 displaystyle P 1 2 1 O halde XX1 X12 4 displaystyle XX 1 X 1 2 4 X3 XX1 1 2 9 displaystyle X 3 XX 1 1 2 9 Z3 4X1 XX1 AX1 1 24 displaystyle Z 3 4X 1 XX 1 AX 1 1 24 Sonuc olarak buldugumuz nokta P3 X3 Z3 9 24 displaystyle P 3 X 3 Z 3 9 24 dikkat edilirse P3 2P1 displaystyle P 3 2P 1 Nokta ToplamaP1 x1 y1 displaystyle P 1 x 1 y 1 P2 x2 y2 displaystyle P 2 x 2 y 2 afin koordinatlarda Montgomery egrisi MA B displaystyle M A B uzerinde iki nokta olmak uzere P3 P1 P2 displaystyle P 3 P 1 P 2 seklinde belirlenen nokta geometrik olarak MA B displaystyle M A B ile P1 displaystyle P 1 ve P2 displaystyle P 2 noktalarini birlestiren dogrunun kesimini ifade eden ucuncu bir noktadir Bu noktanin koordinatlari x3 y3 displaystyle x 3 y 3 asagidaki sekilde belirlenir 1 2 boyutlu afin uzayda y lx m displaystyle y lx m dogrusunun P1 displaystyle P 1 ve P2 displaystyle P 2 noktalarindan gectigini varsayalim bu varsayimdan yararlanarak l y2 y1x2 x1 displaystyle l frac y 2 y 1 x 2 x 1 ve m y1 y2 y1x2 x1 x1 displaystyle m y 1 left frac y 2 y 1 x 2 x 1 right x 1 elde edilir 2 Dogru ile MA B displaystyle M A B egri denklemindeki y displaystyle y degiskeni y lx m displaystyle y lx m ile degistirilirse asagidaki 3 dereceden denklem elde edilir x3 A Bl2 x2 1 2Blm x Bm2 0 displaystyle x 3 A Bl 2 x 2 1 2Blm x Bm 2 0 Daha once gozlemlenebildigi gibi bu denklem P1 displaystyle P 1 P2 displaystyle P 2 ve P3 displaystyle P 3 noktalarinin x koordinatlarina gore uc koke sahiptir Oyleyse denklem x x1 x x2 x x3 0 displaystyle x x 1 x x 2 x x 3 0 seklinde yazilir 3 Yukarida verilen iki ozdes denklemin katsayilarinin ozellikle de ikinci mertebeden olanin terimlerinin katsayilarinin karsilastirilmasiyla asagidaki denklem elde edilir x1 x2 x3 A Bl2 displaystyle x 1 x 2 x 3 A Bl 2 Boylelikle x3 displaystyle x 3 terimi x1 displaystyle x 1 y1 displaystyle y 1 x2 displaystyle x 2 y2 displaystyle y 2 terimleri cinsinden asagidaki bicimde yazilabilir x3 B y2 y1x2 x1 2 A x1 x2 displaystyle x 3 B left frac y 2 y 1 x 2 x 1 right 2 A x 1 x 2 4 P3 displaystyle P 3 noktasinin y displaystyle y koordinatini bulabilmek icin x3 displaystyle x 3 degerini y lx m displaystyle y lx m dogrusunda yerine koymak yeterlidir Bunun dogrudan P3 displaystyle P 3 noktasini vermeyecegine dikkat edin Gercekten bu yontemle R P1 P2 P displaystyle R P 1 P 2 P infty saglayan R displaystyle R noktasinin koordinatlari bulunur Eger P1 displaystyle P 1 ve P2 displaystyle P 2 nokta ekleme isleminin sonuc noktasina ihtiyac duyulursa R P1 P2 P displaystyle R P 1 P 2 P infty ancak ve ancak R P1 P2 displaystyle R P 1 P 2 olmasi durumunu goz onune almak gereklidir Bu yuzden verilen R displaystyle R noktasi icin R displaystyle R noktasini bulmak gereklidir Bu islem verilen R displaystyle R nin y koordinatinin isaretini degistirerek kolaylikla yapilabilir Baska bir deyisle dogru denkleminde x3 displaystyle x 3 un yerine konulmasiyla elde edilen y displaystyle y koordinatinin isaretini degistirmek yeterli olacaktir Oyleyse P3 x3 y3 displaystyle P 3 x 3 y 3 noktasinin koordinatlari P3 P1 P2 displaystyle P 3 P 1 P 2 sunlardir x3 B y2 y1 2 x2 x1 2 A x1 x2 B x2y1 x1y2 2x1x2 x2 x1 2 displaystyle x 3 frac B y 2 y 1 2 x 2 x 1 2 A x 1 x 2 frac B x 2 y 1 x 1 y 2 2 x 1 x 2 x 2 x 1 2 y3 2x1 x2 A y2 y1 x2 x1 B y2 y1 3 x2 x1 3 y1 displaystyle y 3 frac 2x 1 x 2 A y 2 y 1 x 2 x 1 frac B y 2 y 1 3 x 2 x 1 3 y 1 Nokta Ikileme MA B displaystyle M A B Montgomery Egrisi uzerinde verilen bir P1 displaystyle P 1 noktasi icin 2 P1 displaystyle 2 P 1 Geometrik olarak egri ile P1 displaystyle P 1 eget olan dogru arasindaki kesisimi ifade eden ucuncu noktasini temsil eder P3 2P1 displaystyle P 3 2P 1 saglayan P3 displaystyle P 3 noktasinin koordinatlarini bulabilmek icin nokta toplama metodundakine benzer bir yol izlenir ancak bu durumda y lx m dogrusu P1 displaystyle P 1 egrisine teget olmalidir Bu yuzden eger MA B f x y 0 displaystyle M A B f x y 0 ile f x y x3 Ax2 x By2 displaystyle f x y x 3 Ax 2 x By 2 Dogrunun egimini temsil eden l degeri asagidaki gibi verilir l f x f y displaystyle l left frac partial f partial x right frac partial f partial y ne gore yazilabilir Yani l 3x12 2Ax1 12By1 displaystyle l frac 3x 1 2 2Ax 1 1 2By 1 ve P3 displaystyle P 3 P3 2P1 displaystyle P 3 2P 1 x3 Bl2 A x1 x1 B 3x12 2Ax1 1 2 2By1 2 A x1 x1 x12 1 24By12 x12 1 24x1 x12 Ax1 1 y3 2x1 x1 A l Bl3 y1 2x1 x1 A 3x12 2Ax1 1 2By1 B 3x12 2Ax1 1 3 2By1 3 y1 displaystyle begin aligned x 3 amp Bl 2 A x 1 x 1 frac B 3x 1 2 2Ax 1 1 2 2By 1 2 A x 1 x 1 amp frac x 1 2 1 2 4By 1 2 frac x 1 2 1 2 4x 1 x 1 2 Ax 1 1 8pt y 3 amp 2x 1 x 1 A l Bl 3 y 1 amp frac 2x 1 x 1 A 3 x 1 2 2Ax 1 1 2By 1 frac B 3 x 1 2 2Ax 1 1 3 2By 1 3 y 1 end aligned Bukulmus Edwards egrileri ile denkligiKabul edelim ki K displaystyle K karakteristigi 2 den farkli bir cisim olsun Yine kabul edelim ki MA B displaystyle M A B Montgomery formunda bir eliptik egri olsun MA B Bv2 u3 Au2 u displaystyle M A B Bv 2 u 3 Au 2 u A K 2 2 displaystyle A in K smallsetminus 2 2 B K 0 displaystyle B in K smallsetminus 0 ve kabul edelim ki Ea d displaystyle E a d bukulmus Edwards formunda bir eliptik egri olsun Ea d ax2 y2 1 dx2y2 displaystyle E a d ax 2 y 2 1 dx 2 y 2 a d K 0 a d displaystyle a d in K smallsetminus 0 quad a neq d Asagidaki teoremi Mongomery egrileri ile bukulmus Edwards egrileri arasindaki gosterir Teorem i K displaystyle K uzerinde her bukulmus Edwards egrisi bir Montgomery egrisine birasyonel denktir Ozellikle Ea d displaystyle E a d bukulmus Edwards egrisi MA B displaystyle M A B Montgomery egrisine A 2 a d a d displaystyle A frac 2 a d a d ve B 4a d displaystyle B frac 4 a d saglaniyorken birasyonel denktir Esleme ps Ea d MA B displaystyle psi E a d rightarrow M A B x y u v 1 y1 y 1 y 1 y x displaystyle x y mapsto u v left frac 1 y 1 y frac 1 y 1 y x right Ea d displaystyle E a d den MA B displaystyle M A B ye birasyonel denklik tersi ps 1 displaystyle psi 1 MA B Ea d displaystyle M A B rightarrow E a d u v x y uv u 1u 1 a A 2B d A 2B displaystyle u v mapsto x y left frac u v frac u 1 u 1 right a frac A 2 B d frac A 2 B Dikkat edilirse iki egri arasindaki bu denklik her yerde gecerli degildir gercekten de ps displaystyle psi eslemesi MA B displaystyle M A B de v 0 displaystyle v 0 ya da u 1 0 displaystyle u 1 0 noktalarinda tanimli degildir Weierstrass egrileri ile denkligiTum eliptik egriler Weierstrass formunda yazilabilir Ozellikle Montgomery formundaki eliptik egriyi ele alalim MA B displaystyle M A B By2 x3 Ax2 x displaystyle By 2 x 3 Ax 2 x asagidaki sekilde donusturulebilir MA B displaystyle M A B nin her bir terimini B3 displaystyle B 3 e bolup ve x y degerlerine u xB displaystyle u frac x B v yB displaystyle v frac y B donusumu uygulanirsa v2 u3 ABu2 1B2u displaystyle v 2 u 3 frac A B u 2 frac 1 B 2 u Bir kisa Weierstrass formu elde edebilmek icin burada u yu t A3B displaystyle t frac A 3B degeri ile degistirtirmek gerekir v2 t A3B 3 AB t A3B 2 1B2 t A3B displaystyle v 2 left t frac A 3B right 3 frac A B left t frac A 3B right 2 frac 1 B 2 left t frac A 3B right Sonuc olarak v2 t3 3 A23B2 t 2A3 9A27B3 displaystyle v 2 t 3 left frac 3 A 2 3B 2 right t left frac 2A 3 9A 27B 3 right Dolayisiyla esleme soyle verilir ps displaystyle psi MA B Ea b displaystyle M A B rightarrow E a b x y t v xB A3B yB a 3 A23B2 b 2A3 9A27B3 displaystyle x y mapsto t v left frac x B frac A 3B frac y B right a frac 3 A 2 3B 2 b frac 2A 3 9A 27B 3 aksine F displaystyle mathbb F baz cismi uzerinde Weierstrass formunda bir eliptik egri Ea b displaystyle E a b v2 t3 at b displaystyle v 2 t 3 at b Montgomery formuna ancak ve ancak Ea b displaystyle E a b mertebesi 4 e bolunebilirse ve asagidaki kosullari saglarsa donusturulebilir z3 az b 0 displaystyle z 3 az b 0 en az bir a F displaystyle alpha in mathbb F kokune sahip ve 3a2 a displaystyle 3 alpha 2 a F displaystyle mathbb F de bir ikinci dereceden rezidu Bu sartlar saglandiginda s 3a2 a 1 displaystyle s sqrt 3 alpha 2 a 1 icin asagidaki eslemeye sahip olunur ps 1 displaystyle psi 1 Ea b MA B displaystyle E a b rightarrow M A B t v x y s t a sv A 3as B s displaystyle t v mapsto x y left s t alpha sv right A 3 alpha s B s Ayrica bakinizCurve25519 Curve25519 Eliptik egri kriptografisiNotlar 1987 Speeding the Pollard and Elliptic Curve Methods of Factorization Mathematics of Computation 48 177 ss 243 264 doi 10 2307 2007888 JSTOR 2007888 Peter Birkner Marc Joye Tanja Lange and Christiane Peters 2008 Twisted Edwards Curves PDF Springer Verlag Berlin Heidelberg ISBN 978 3 540 68159 5 KB1 bakim Birden fazla ad yazar listesi link olu kirik baglanti Katsuyuki Okeya Hiroyuki Kurumatani and Kouichi Sakurai 2000 Elliptic Curves with the Montgomery Form and Their Cryptographic Applications Public Key Cryptography PKC2000 8 Mart 2018 tarihinde kaynagindan Erisim tarihi 11 Nisan 2018 KB1 bakim Birden fazla ad yazar listesi link Kaynakca 1987 Speeding the Pollard and Elliptic Curve Methods of Factorization Mathematics of Computation 48 177 ss 243 264 doi 10 2307 2007888 JSTOR 2007888 Peter Birkner Marc Joye Tanja Lange and Christiane Peters 2008 Twisted Edwards Curves PDF Springer Verlag Berlin Heidelberg ISBN 978 3 540 68159 5 KB1 bakim Birden fazla ad yazar listesi link olu kirik baglanti Wouter Castryck Steven Galbraith Reza Rezaeian Farashahi 2008 PDF 29 Temmuz 2016 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 11 Nisan 2018
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans



















































