Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Fizikte Net Kuvvet, bir cisim üzerine etkiyen kuvvetlerin toplamına eşittir. Net kuvvetin hesaplanması için serbest cisim diyagramı oluşturulur ve ortamdan izole edilerek cisme etkiyen kuvvetler vektörel olarak yazılır. Net kuvvetin cisme olan etkisi net kuvvetin yönüyle aynı olmak zorunda değildir. Bu etkiyi hesaplamak için bileşke kuvvet'in ve tork'un hesaplanması gerekir. Çünkü cisme uygulanan kuvvet tek bir nokta olarak düşünülmeyen cisimlerde bir tork yaratabilir ve bu da bileşke kuvvetin net kuvvetten farklı olmasına sebep olabilir. Kuvvetin cisme etki ettiği nokta göz önünde bulundurularak hesaplanan tork ile beraber net kuvvet bize bileşke kuvveti verir. Ve cisim bileşke kuvvetin öne sürdüğü doğrultuda hareket eder.
Toplam Kuvvet
Toplam kuvvet, ki aynı zamanda net kuvvet ile aynı anlama gelir, cisme etki eden tüm kuvvetlerin toplamına eşittir. Newton’un ikinci yasası'ndan yola çıkarak, bu toplam kuvvetin cisme verdiği ivme kuvvetlerin verdiği toplam ivmelenmeye eşittir.
Kuvvet, vektörel bir büyüklüktür. Bu sebeple bir doğrultusu ve büyüklüğü vardır. Bu özelliği belirtmek için kuvvetin sembolü 
olarak gösterilir. Bir vektör yazılırken kuvvetin etkidiği bir A noktası belirtilir ve bir B noktasına kadar ok işareti şeklinde çizilir. Bu ok işareti vektörün yönünü A B noktaları arası mesafe de vektörün büyüklüğünü verir.
Vektör hesaplamaları 1800'lerin sonları ve 1900'lerin başları arasında geliştirilmiştir fakat birazdan bahsedeceğimiz paralelkenar yöntemi'nin Antik Yunanistan'dan kalma olduğu hem Newton hem de Galileo tarafından belirtilmiştir.
Buradaki diyagramda da görüldüğü üzere vektörel olarak belirtilmiş F1 ve F2 kuvvetleri paralelkenar yöntemiyle toplanmıştır. Bunun için kuvvetler paralelkenarın farklı iki kenarı olarak düşünülmüş ve bu paralelkenarın bu iki kuvvetin başlangıç noktasından çıkan kirişi toplam kuvveti vermiştir.
Fakat iki vektörü toplamak veya çıkartmak için bu vektörlerin aynı noktaya uygulanıyor olması gerekir. Kuvvetler de birer vektör olduğu için farklı noktalarına kuvvet uygulanan bir cismin hareketini incelemek için bir nokta belirlenir (genelde kütle merkezi seçilir) ve bu noktaya göre tork alınarak bileşke kuvvet bulunur.
Paralelkenar Kenar Yöntemi
Kuvvet bir vektör olduğu için yönü, büyüklüğü ve bir uygulanma noktası bulunur. Bu kuvvet vektörünü (F) tanımlamak için şu açıklamayı yapabiliriz. Bir A ve B noktası belirleyelim ve bu vektörümüzü Adan B ye bir ok şeklinde çizelim. Ayrıca iki noktayı da uzayda A=(Ax,Ay,Az) ve B=(Bx, By, Bz) olarak tanımlarsak
bize F vektörümüzü verir. Bu vektörün büyüklüğü de
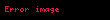
şeklindedir.
Bu aşamadan sonra yapmamız gereken F1=B-A ve F2=D-A olarak tanımladığımız kuvvet vektörlerimizde yukarıdaki mantığı uygulamaktır. F1+F2 işlemini yapmak için
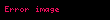
yazılabilir ki bu da ayrıca
Şeklinde yazılabilir. Burada B ve D noktalarının orta noktası E noktası olduğu için (B+D)/2 işlemi E şeklinde yazılabilir. Ayrıca iki tane E-A bize C-A’yı verir ki bu da bizim vektörlerimizin toplamıdır. Bu uzun işlemleri yapmaktansa düzgünce çizilen iki vektörü, aynılarından karşıya ekleyerek bir paralelkenar oluşturmak ve sonra da bir uçtan diğer uca bir CA doğrusu çizmek bize toplama işlemini yaptıracaktır. İşte bu yönteme paralelkenar yöntemi denir.
Doğrusal ve Dairesel Hareket
Noktasal kuvvet
Bir kuvvet cisme etki ettiğinde, bu tek bir noktadan olur. Bu aşamada kuvvetin etkidiği alan hacimsiz sayılır ve buna noktasal kuvvet denir. Etki ettiği yüzeye de etkime noktası. Fakat gerçek hayatta hacim yok sayılamaz ve kuvvet birkaç farklı noktaya dağılmış şekilde etki eder. Fakat bu cismin dönme hareketini incelerken sorunlara yol açabilir ve bunun giderilmesi için aşağıdaki maddelerle çözümlenir.
Genellikle kuvvetin uygulandığı alan cisme göre ufak kalır ve bu nedenle yaklaşık bir nokta belirlenir ve bu varsayım üzerinden işlemler yapılır. Hata payının yüksek çıkıp çıkmadığı kolaylıkla saptanabilir.
Eğer kuvvetin uygulandığı alan bir varsayım yapacak kadar küçük değilse veya bütün parçacıklara uygulanıyorsa(yerçekimi kuvveti gibi), o zaman işlem bütün parçacıklar için tek tek yapılır. Bunun için diferansiyel denklemler ve integral matematiği kullanılır. Düzgün yerçekimsel kuvvet gibi çok nadir durumlarda ise cisim tek bir noktaya indirgenerek işlem yapılabilir. Her hangi işlemler uygulanacak olursa olsun, katı cisimlerdeki problemlere yaklaşımda ilk olarak kuvvetlerin gösterildiği bir model, noktasal kuvvet modeli, çizilir.
Katı Cisimler
Bu örnekte sahip olduğumuz bir F kuvveti H noktasından cisme etki ediyor. C noktasını cismin merkezi farz edersek ve cismin m kütlesinde olduğunu var sayarsak buradan cismin merkezinin ivmesi
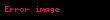
Ve cismin açısal ivmesi de
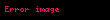
olarak karşımıza çıkar. Buradaki 
, tork ve I ise eylemsizlik momentidir. Buradaki torkun kuvvetle olan bağıntısı ise
şeklindedir. Buradaki 
pozisyon vektörü olup şekilde de gözüktüğü gibi cismin merkezinden kuvvetin uygulandığı etkileşim noktasınadır.
Tork vektörü uygulanan kuvvete ve aynı zamanda da pozisyon vektörüne diktir. Ancak hangi yöne olduğunu bulmak için sağ el kuralı uygulanmalıdır. Bu örnekte tork vektörü kâğıttan dışarı, gözlemciye doğrudur.
Eylemsizlik momenti de cismin merkezinden geçen ve aynı zamanda da tork vektörüne paralel olan bir doğru çizilerek bulunur. Cisimlerin şekilleri ve kütleleriyle doğrudan alakalıdır.
Bileşke Kuvvet
Katı cisimlerin hareketini incelerken bakılması gereken iki şey bileşke kuvvet ve tork'tur. Ama nadiren de olsa tork sıfır olabilir. Buna torksuz bileşke denir.
1.Şekilde bileşke kuvvet bulmak için bu iki kuvvettin birleşme noktaları hesaba katılır. Örnekte olduğu gibi birleşebilen bu kuvvetin bileşkesi paralelkenar yöntemiyle rahatlıkla bulunabilir. Bu yöntemdeki amaç ortak kesişim noktasını gözlem noktası almaktır. Bu sayede tork her zaman sıfırdır ve bu sayede bileşke kuvvet net kuvvete eşittir.
2.Şekilde ise birbirine paralel iki kuvvetin bileşkesi alınmakta. Bu iki kuvvet paralel oldukları için direkt olarak birbirlerinin üzerine eklenerek işlem yapılabilir. Buradaki tork sorunu ise kuvvetlerin paralel ve aynı yönlü olması sayesinde kendiliğinden çözülür. Gözlem noktası farkı olmadan tork sıfıra eşittir.
3. Şekilde ise kuvvetler farklı zıt yönlü ve eşit büyüklükte olduğu için net kuvvet sıfıra eşittir. Fakat bu örnekte tork mevcuttur ve 
formülü ile bulunabilir.
Kullanım
Genel olarak bir sisteme etki eden kuvvet bir net kuvvet ve ona bağlı bir tork ile ifade edilebilir. Bunun için yukarıda bahsedilen çözümler uygulanabilir. Burada açıklanmış durumun aksine bazı yazılarda net kuvvet ve bileşke kuvvetin eş anlamlı olarak kullanıldığının da altından geçmek gerekir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte Net Kuvvet bir cisim uzerine etkiyen kuvvetlerin toplamina esittir Net kuvvetin hesaplanmasi icin serbest cisim diyagrami olusturulur ve ortamdan izole edilerek cisme etkiyen kuvvetler vektorel olarak yazilir Net kuvvetin cisme olan etkisi net kuvvetin yonuyle ayni olmak zorunda degildir Bu etkiyi hesaplamak icin bileske kuvvet in ve tork un hesaplanmasi gerekir Cunku cisme uygulanan kuvvet tek bir nokta olarak dusunulmeyen cisimlerde bir tork yaratabilir ve bu da bileske kuvvetin net kuvvetten farkli olmasina sebep olabilir Kuvvetin cisme etki ettigi nokta goz onunde bulundurularak hesaplanan tork ile beraber net kuvvet bize bileske kuvveti verir Ve cisim bileske kuvvetin one surdugu dogrultuda hareket eder Toplam KuvvetToplam kuvvet ki ayni zamanda net kuvvet ile ayni anlama gelir cisme etki eden tum kuvvetlerin toplamina esittir Newton un ikinci yasasi ndan yola cikarak bu toplam kuvvetin cisme verdigi ivme kuvvetlerin verdigi toplam ivmelenmeye esittir Kuvvet vektorel bir buyukluktur Bu sebeple bir dogrultusu ve buyuklugu vardir Bu ozelligi belirtmek icin kuvvetin sembolu F displaystyle vec F olarak gosterilir Bir vektor yazilirken kuvvetin etkidigi bir A noktasi belirtilir ve bir B noktasina kadar ok isareti seklinde cizilir Bu ok isareti vektorun yonunu A B noktalari arasi mesafe de vektorun buyuklugunu verir Vektor hesaplamalari 1800 lerin sonlari ve 1900 lerin baslari arasinda gelistirilmistir fakat birazdan bahsedecegimiz paralelkenar yontemi nin Antik Yunanistan dan kalma oldugu hem Newton hem de Galileo tarafindan belirtilmistir Addition of forces Buradaki diyagramda da goruldugu uzere vektorel olarak belirtilmis F1 ve F2 kuvvetleri paralelkenar yontemiyle toplanmistir Bunun icin kuvvetler paralelkenarin farkli iki kenari olarak dusunulmus ve bu paralelkenarin bu iki kuvvetin baslangic noktasindan cikan kirisi toplam kuvveti vermistir Fakat iki vektoru toplamak veya cikartmak icin bu vektorlerin ayni noktaya uygulaniyor olmasi gerekir Kuvvetler de birer vektor oldugu icin farkli noktalarina kuvvet uygulanan bir cismin hareketini incelemek icin bir nokta belirlenir genelde kutle merkezi secilir ve bu noktaya gore tork alinarak bileske kuvvet bulunur Paralelkenar Kenar YontemiParallelogram1 Kuvvet bir vektor oldugu icin yonu buyuklugu ve bir uygulanma noktasi bulunur Bu kuvvet vektorunu F tanimlamak icin su aciklamayi yapabiliriz Bir A ve B noktasi belirleyelim ve bu vektorumuzu Adan B ye bir ok seklinde cizelim Ayrica iki noktayi da uzayda A Ax Ay Az ve B Bx By Bz olarak tanimlarsak F B A Bx Ax By Ay Bz Az displaystyle F B A B x A x B y A y B z A z bize F vektorumuzu verir Bu vektorun buyuklugu de F Bx Ax 2 By Ay 2 Bz Az 2 displaystyle left F right sqrt B x A x 2 B y A y 2 B z A z 2 seklindedir Bu asamadan sonra yapmamiz gereken F1 B A ve F2 D A olarak tanimladigimiz kuvvet vektorlerimizde yukaridaki mantigi uygulamaktir F1 F2 islemini yapmak icin F F1 F2 B A D A displaystyle F F 1 F 2 B A D A yazilabilir ki bu da ayrica F F1 F2 2 B D2 A 2 E A displaystyle F F 1 F 2 2 left frac B D 2 A right 2 left E A right Seklinde yazilabilir Burada B ve D noktalarinin orta noktasi E noktasi oldugu icin B D 2 islemi E seklinde yazilabilir Ayrica iki tane E A bize C A yi verir ki bu da bizim vektorlerimizin toplamidir Bu uzun islemleri yapmaktansa duzgunce cizilen iki vektoru aynilarindan karsiya ekleyerek bir paralelkenar olusturmak ve sonra da bir uctan diger uca bir CA dogrusu cizmek bize toplama islemini yaptiracaktir Iste bu yonteme paralelkenar yontemi denir Dogrusal ve Dairesel HareketNoktasal kuvvet Bir kuvvet cisme etki ettiginde bu tek bir noktadan olur Bu asamada kuvvetin etkidigi alan hacimsiz sayilir ve buna noktasal kuvvet denir Etki ettigi yuzeye de etkime noktasi Fakat gercek hayatta hacim yok sayilamaz ve kuvvet birkac farkli noktaya dagilmis sekilde etki eder Fakat bu cismin donme hareketini incelerken sorunlara yol acabilir ve bunun giderilmesi icin asagidaki maddelerle cozumlenir Genellikle kuvvetin uygulandigi alan cisme gore ufak kalir ve bu nedenle yaklasik bir nokta belirlenir ve bu varsayim uzerinden islemler yapilir Hata payinin yuksek cikip cikmadigi kolaylikla saptanabilir Eger kuvvetin uygulandigi alan bir varsayim yapacak kadar kucuk degilse veya butun parcaciklara uygulaniyorsa yercekimi kuvveti gibi o zaman islem butun parcaciklar icin tek tek yapilir Bunun icin diferansiyel denklemler ve integral matematigi kullanilir Duzgun yercekimsel kuvvet gibi cok nadir durumlarda ise cisim tek bir noktaya indirgenerek islem yapilabilir Her hangi islemler uygulanacak olursa olsun kati cisimlerdeki problemlere yaklasimda ilk olarak kuvvetlerin gosterildigi bir model noktasal kuvvet modeli cizilir Kati Cisimler Free body acceleration Bu ornekte sahip oldugumuz bir F kuvveti H noktasindan cisme etki ediyor C noktasini cismin merkezi farz edersek ve cismin m kutlesinde oldugunu var sayarsak buradan cismin merkezinin ivmesi a F m displaystyle vec a frac vec F m Ve cismin acisal ivmesi de a T I displaystyle vec alpha frac vec T I olarak karsimiza cikar Buradaki T displaystyle vec T tork ve I ise eylemsizlik momentidir Buradaki torkun kuvvetle olan bagintisi ise T r xF displaystyle vec T vec r x vec F seklindedir Buradaki r displaystyle vec r pozisyon vektoru olup sekilde de gozuktugu gibi cismin merkezinden kuvvetin uygulandigi etkilesim noktasinadir Tork vektoru uygulanan kuvvete ve ayni zamanda da pozisyon vektorune diktir Ancak hangi yone oldugunu bulmak icin sag el kurali uygulanmalidir Bu ornekte tork vektoru kagittan disari gozlemciye dogrudur Eylemsizlik momenti de cismin merkezinden gecen ve ayni zamanda da tork vektorune paralel olan bir dogru cizilerek bulunur Cisimlerin sekilleri ve kutleleriyle dogrudan alakalidir Bileske KuvvetKati cisimlerin hareketini incelerken bakilmasi gereken iki sey bileske kuvvet ve tork tur Ama nadiren de olsa tork sifir olabilir Buna torksuz bileske denir Rezultanta 1 Sekilde bileske kuvvet bulmak icin bu iki kuvvettin birlesme noktalari hesaba katilir Ornekte oldugu gibi birlesebilen bu kuvvetin bileskesi paralelkenar yontemiyle rahatlikla bulunabilir Bu yontemdeki amac ortak kesisim noktasini gozlem noktasi almaktir Bu sayede tork her zaman sifirdir ve bu sayede bileske kuvvet net kuvvete esittir 2 Sekilde ise birbirine paralel iki kuvvetin bileskesi alinmakta Bu iki kuvvet paralel olduklari icin direkt olarak birbirlerinin uzerine eklenerek islem yapilabilir Buradaki tork sorunu ise kuvvetlerin paralel ve ayni yonlu olmasi sayesinde kendiliginden cozulur Gozlem noktasi farki olmadan tork sifira esittir 3 Sekilde ise kuvvetler farkli zit yonlu ve esit buyuklukte oldugu icin net kuvvet sifira esittir Fakat bu ornekte tork mevcuttur ve T Fd displaystyle T Fd formulu ile bulunabilir KullanimGenel olarak bir sisteme etki eden kuvvet bir net kuvvet ve ona bagli bir tork ile ifade edilebilir Bunun icin yukarida bahsedilen cozumler uygulanabilir Burada aciklanmis durumun aksine bazi yazilarda net kuvvet ve bileske kuvvetin es anlamli olarak kullanildiginin da altindan gecmek gerekir