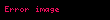Newton'un evrensel çekim yasası (klâsik mekaniğin bir parçasıdır) aşağıdaki gibi ifade edilir;

Her bir noktasal kütle diğer noktasal kütleyi, ikisini birleştiren bir çizgi doğrultusundaki bir kuvvet ile çeker. Bu kuvvet bu iki kütlenin çarpımıyla doğru orantılı, aralarındaki mesafenin karesi ile ters orantılıdır:
Burada:
- F iki kütle arasındaki çekim kuvvetinin büyüklüğü,
- G Evrensel çekim sabiti 6.67 × 10-11 N m2 kg-2 ,
- m1 birinci kütlenin büyüklüğü,
- m2 ikinci kütlenin büyüklüğü,
- r ise iki kütle arasındaki mesafedir.
SI birimlerinde, F Newton (N), m1 ve m2 kilogram(kg), r Metre (m) dir ve G sabiti yaklaşık olarak 6.67×10−11 N m2 kg−2’a eşittir. G ilk kez İngiliz bilim insanı Henry Cavendish tarafından, "Philosophiae Naturalis Principia Mathematica"nın basımından 111 ve Newton’un ölümünden 71 yıl sonra ölçülmüştür; bu yüzden Newton’un hesaplamalarının hiçbirinde “G” sabiti kullanılmamış, bunun yerine bir kuvvete bağıl başka bir kuvvet hesaplamıştır.
Newton’un çekim yasası Coulomb yasası’na benzer. Newton’un yasası iki kütle arasındaki çekim kuvvetini hesaplamak için kullanılırken, benzer şekilde, Coulomb yasası yüklü iki iletkenin arasındaki elektriksel kuvvetin büyüklüğünü hesaplamak için kullanılır. Coulomb yasası’nun denkleminde Newton’un denklemindeki kütlelerin yerine yüklerin çarpımını içerir. Böylece Coulomb yasası’na göre elektriksel kuvvet yüklerin çarpımının aralarındaki mesafeye bölümüyle doğru orantılıdır.
Yerçekimi ivmesi
a1’e birinci kütleye etkiyen yerçekimi ivmesi diyelim. Newton’un ikinci yasasına göre F = m1a1, a1 = F / m1’dır. Fi önceki denklemden yerine koyarsak:
olur.
Aynı şekilde a2’de buna benzerdir.
SI birimlerinde, yerçekimi ivmesi (veya genel olarak ivme), metrenin saniyenin karesine oranıdır (m/s2 or m s−2). SI olmayan birimlerde ise birimi Galileo (Gal), g-kuvveti (İng. İngilizce: g-force), ayak bölü saniyenin karesidir.
Bir kütleyi Dünya'ya çeken kuvvet, aynı zamanda Dünya'yı da kütleye doğru çeker. Bunların ivmeleri ise aşağıdaki gibi hesaplanır:
Eğer m1m2’ye göre göz ardı edilebilirse, küçük kütleler yaklaşık olarak aynı ivmeye sahip olur. Bununla beraber m1 epeyce büyükse birleşik ivme göz önüne alınmalıdır.
Eğer r bir objenin yörüngesi boyunca oransal olarak çok az değişirse – bir objenin Dünya'nın yüzeyine yakın bir yerde düşmesi gibi – yerçekimi ivmesi sabite oldukça yakın olur. Büyük bir kitle boyunca, “r”deki değişiklikler ve yer çekimi kuvvetindeki ardı ardına değişiklikler gözle görülür bir gel-git kuvveti oluşturabilir. Örneğin, Dünya'nın yakın ve uzak yüzleri ile Ay arasındaki mesafe farkı 6.350 km dir. 385.000 km ortalama mesafeye göre küçük bir fark olsa da bu, Ay'ın Dünya'nın okyanusları üzerinde bir çekim kuvveti oluşturmasını ve böylece gelgit oluşumuna sebep olur.
Uzaysal boyutu olan kütleler
Eğer ilgilenilen kütlelerin uzaysal boyutu varsa (teorik olarak noktasal olmaktan ziyade) o zaman aralarındaki çekim kuvveti, bu kütleleri oluşturan kavramsal noktaların katkılarının toplanmasıyla hesaplanır. Limitte bileşen nokta kütleler sonsuz derecede küçüldükçe, kuvvetin (aşağıda vektör formu görülüyor) iki fiziksel kütlenin boyutlarına oranlarının integrali gerekir.
Bu yolla kütlesi küresel olarak simetrik dağılmış kütle, haricî kütlelere tüm objelerin kütleleri merkezindeki bir nokta etrafında toplanmış gibi aynı çekim etkisini uygular. (Bu, genellikle küresel simetrik olmayan kütleler için geçerli değildir.)
Küresel simetrik dağılımlı bir malzemenin içindeki kütlelerin çekimsel kuvvetini bulmak için Newton’un kabuk teoremi (İng. İngilizce: Shell’s theorem) kullanılabilir. Bu teorem, bize kütle dağılımının farklı parçalarının kütle dağılım merkezinden r0 kadar uzaktaki bir parçayı nasıl etkilediklerini açıklar:
- r < r0 yarıçapında bulunan kütle, r0’da sanki kütlenin tamamı bu yarıçapta bir küredeki tüm kütlenin kütle dağılımı merkezinde toplanmış gibi aynı kuvvete sebep olur (yukarıda yazıldığı gibi).
- r > r0 yarıçapında bulunan kütle r0’ da net çekim kuvveti oluşturmaz. Örneğin, r0 noktasındaki kürenin elementleri tarafından etkilenen münferit kuvvetler birbirlerini götürürler.
Örneğin, bir sonuç olarak, eşit dağılan bir kalınlık ve yoğunluğa sahip olan bir kabuk boyunca net çekim kuvveti sıfırdır.
Vektör formu


Newton’un evrensel çekim yasası, hem çekim kuvvetinin büyüklüğünü hem de doğrultusunu gösteren bir vektör olarak yazılabilir. Bu formülde kalın yazılar vektörleri göstermektedir:
Burada
1 numaralı cismin 2 numaralıya uyguladığı kuvvet,
: çekim sabiti (yerçekimi sabiti olan g ile karıştırılmamalı),
ve
sırasıyla birinci ve ikinci objelerin kütleleri,
1 ve 2 objeleri arasındaki mesafe,
ise 1’inci objeden 2.’ye olan birim vektördür.
Eşitliğin vektörel formunun, F nin artık vektörel bir değer olması ve sağ tarafın uygun birim vektörle çarpılmış olması haricinde, daha önceden verilen skaler formla aynı olduğu görülebilir. Ayrıca buradan şu da görülebilir: F12 = - F21.
Çekim Alanı
Çekim alanı uzayda verilen herhangi bir noktadaki objeye, birim kütle başına uygulanan çekim kuvvetini tanımlayan vektör alanıdır. Aslında bu o noktadaki çekim ivmesine eşittir.
Eğer birden fazla obje varsa(dünya ve ay arasındaki bir roket gibi) kullanışlı hale gelen bir genelleştirmedir. İki obje için(örneğin obje 2 bir roket ve obje 1 de dünya olsun) basitçe 

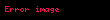

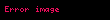
Böylece:
olur.
Bu formül alana sebep olan objelerden bağımsızdır. Bu alan ivme birimlerine sahiptir ve bu da SI birimlerinde m/s2’dir.
Çekim alanları aynı zamanda korunumlu alanlardır, yani, bir pozisyondan öbürüne çekim tarafından yapılan iş yoldan bağımsızdır. Bunun sonucunda potansiyel aşağıdaki gibi potansiyel V(r) alanı oluşur:
.
Eğer m1 noktasal bir kuvvet ise veya homojen dağılmış bir kütle ise, kürenin dışındaki kuvvet alanı g(r) izotropiktir (yönden bağımsızdır), örneğin, sadece kürenin merkezinden olan r mesafesine bağlıdır. Bu durumda;
Newton’un teorisinin problemleri
Newton'un tanımı birçok pratik amaç için yeterli şekilde doğrudur ve bu yüzden geniş şekilde kullanılır. Boyutsuz değerler φ/c2 ve (v/c)’nin ikisi de küçük olduğunda kullanılabilir, burada φ çekimsel potansiyel, v incelenen objelerin hızı ve c ışık hızıdır. Örnek olarak, Newtonien çekim Dünya/Güneş sisteminin doğru bir tanımını sağlar, çünkü;
burada rorbit dünyanın güneş etrafındaki yörüngesinin yarıçapıdır.
Boyutsuz değişkenlerden biri büyük olduğu durumlarda, sistemi tanımlamak için genel görelilik kullanılmalıdır. Genel görelilik, küçük potansiyel ve düşük hız sınırlarında Newton'un çekime dönüşür bu yüzden, Newton’un çekim yasası için sıklıkla genel göreliliğin düşük çekim limiti denir.
Teorik kaygılar
- Çekim arabulucusunu hemen bulma gibi bir ihtimal yoktur. Çekimsel kuvvet ile bilinen diğer temel kuvvetler arasındaki ilişkiyi tanımlamak için teorisyenler tarafından yapılan teşebbüsler, 50 yıldır gözle görülür bir ilerleme kaydedilmiş olsa da, henüz sonuca ulaşmamıştır. Newton bile açıklanamaz uzaktan etkileşim konusunda kendini yetersiz hissetmiştir.
- Newton’un teorisi çekimsel kuvvetin ani iletimini gerektirir. Genel göreliliğin geliştirilmesinden önce uzay ve zamanın doğası ile ilgili yapılan klasik varsayımlar, yayılım gecikmesi kararsız yörüngelere sebep olur.
Gözlemle uyuşmazlıklar
- Newton'un teorisi gezegenlerin, özellikle Merkür’ün, yörüngelerinin güneşe en yakın noktalarının(günberi) yalpalamalarını tam olarak açıklamaz. Newton'un tahminlerle, gözlenen yalpalama arasında, diğer gezegenlerin çekimsel sürüklemelerinden kaynaklanan, 43/3600 derecelik(43 arcsecond) bir uyumsuzluk bulunmaktadır.
- Newton’un teorisi kullanılarak tahmin edilen sapma gözlenenin sadece yarısıdır. Genel görelilik ise gözlemlere daha yakındır.
Çekimsel ve ataletsel kütlelerin tüm kütleler için aynı olmasıyla ilgili gözlenen gerçek, Newton’un sisteminde açıklanamamaktadır. Genel görelilik bunu bir varsayım olarak alır.
Newton'un şüpheleri
Newton kendi anıtsal çalışmasında çekim yasasını formüle edebiliyorken, kendi eşitliklerinin öne sürdüğü uzaktan etkileşim(action at a distance) kavramı yüzünden kendini derin şekilde rahatsız hissediyordu. Kendi sözleriyle “ bu gücün sebebini hiçbir zaman tespit edememişti”. Tüm diğer durumlarda, kütleler üzerine etkiyen çeşitli kuvvetlerin sebebini açıklamak için hareket olgusunu kullanmıştır, fakat, çekimle ilgili durumda, çekim kuvvetini üreten hareketi deneysel olarak tanımlayamamıştı. Dahası, yer üzerindeki bu kuvvetin sebebine gelince bir hipotez önermeyi dahi reddediyordu.
“Filozoflar şimdiye kadar çekim kuvvetinin kaynağı için boşuna doğa araştırmasına girişmişlerdir” diye pişman olmuştur, çünkü “birçok sebepten dolayı”, doğa olgusunun temeli olan, “şimdiye kadar bilinmeyen sebepler”in varlığına ikna olmuştur. Bu temel olgular hala araştırılmaktadır ve hipotezler çok olsa da tanımlayıcı yanıt henüz bulunamamıştır. Newton’un 1713 tarihli ve “Principia”nın ikinci baskısı olan “General Scholium”unda:
- "Daha henüz çekimle ilgili bu özelliklerinin sebeplerini olgudan keşfedebilmiş değilim,ve yalandan hipotez uydurmadım…Çekimin varlığı ve açıkladığım yasalara göre işlemesi ve uzaysal kütlelerin(yıldız, gezegen gibi) hesaplamasına yaptığı hizmetler yeterlidir. Bir kütle bir başkasını bir vakum içinde, başka hiçbir şeyin arabuluculuğu olmadan etkiler, etkileri ve kuvvetleri tarafından ve onların içine diğerine taşınabilmesi bence büyük bir garabettir ve bence bu yüzden, felsefi malzemelerde düşünmenin bileşen yetisine sahip hiç kimse, onun içine düşmez."
Kaynakça
- ^ - Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: . Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999
- ^ - Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)
- ^ - The Construction of Modern Science: Mechanisms and Mechanics, by Richard S. Westfall. Cambridge University Press 1978
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Newton un evrensel cekim yasasi klasik mekanigin bir parcasidir asagidaki gibi ifade edilir Newton in evrensel kutlecekimi yasasinin mekanizmasi bir nokta kutle m1 diger bir nokta kutleyi m2 iki kutlenin carpimi ile dogru aralarindaki r uzakliginin karesi ile ters orantili olacak buyuklukteki bir F2 kuvveti ile ceker Kutlelerden ve bu kutlelerin aralarindaki uzakliktan bagimsiz olarak F1 ve F2 kuvvetlerinin buyuklukleri her zaman birbirine esittir G kutlecekim sabitidir Her bir noktasal kutle diger noktasal kutleyi ikisini birlestiren bir cizgi dogrultusundaki bir kuvvet ile ceker Bu kuvvet bu iki kutlenin carpimiyla dogru orantili aralarindaki mesafenin karesi ile ters orantilidir F Gm1m2r2 displaystyle F G frac m 1 m 2 r 2 Burada F iki kutle arasindaki cekim kuvvetinin buyuklugu G Evrensel cekim sabiti 6 67 10 11 N m2 kg 2 m1 birinci kutlenin buyuklugu m2 ikinci kutlenin buyuklugu r ise iki kutle arasindaki mesafedir SI birimlerinde F Newton N m1 ve m2 kilogram kg r Metre m dir ve G sabiti yaklasik olarak 6 67 10 11 N m2 kg 2 a esittir G ilk kez Ingiliz bilim insani Henry Cavendish tarafindan Philosophiae Naturalis Principia Mathematica nin basimindan 111 ve Newton un olumunden 71 yil sonra olculmustur bu yuzden Newton un hesaplamalarinin hicbirinde G sabiti kullanilmamis bunun yerine bir kuvvete bagil baska bir kuvvet hesaplamistir Newton un cekim yasasi Coulomb yasasi na benzer Newton un yasasi iki kutle arasindaki cekim kuvvetini hesaplamak icin kullanilirken benzer sekilde Coulomb yasasi yuklu iki iletkenin arasindaki elektriksel kuvvetin buyuklugunu hesaplamak icin kullanilir Coulomb yasasi nun denkleminde Newton un denklemindeki kutlelerin yerine yuklerin carpimini icerir Boylece Coulomb yasasi na gore elektriksel kuvvet yuklerin carpiminin aralarindaki mesafeye bolumuyle dogru orantilidir Yercekimi ivmesia1 e birinci kutleye etkiyen yercekimi ivmesi diyelim Newton un ikinci yasasina gore F m1a1 a1 F m1 dir Fi onceki denklemden yerine koyarsak a1 Gm2r2 displaystyle a 1 G frac m 2 r 2 olur Ayni sekilde a2 de buna benzerdir SI birimlerinde yercekimi ivmesi veya genel olarak ivme metrenin saniyenin karesine oranidir m s2 or m s 2 SI olmayan birimlerde ise birimi Galileo Gal g kuvveti Ing Ingilizce g force ayak bolu saniyenin karesidir Bir kutleyi Dunya ya ceken kuvvet ayni zamanda Dunya yi da kutleye dogru ceker Bunlarin ivmeleri ise asagidaki gibi hesaplanir a1 a2 Gm1 m2r2 displaystyle a 1 a 2 G frac m 1 m 2 r 2 Eger m1m2 ye gore goz ardi edilebilirse kucuk kutleler yaklasik olarak ayni ivmeye sahip olur Bununla beraber m1 epeyce buyukse birlesik ivme goz onune alinmalidir Eger r bir objenin yorungesi boyunca oransal olarak cok az degisirse bir objenin Dunya nin yuzeyine yakin bir yerde dusmesi gibi yercekimi ivmesi sabite oldukca yakin olur Buyuk bir kitle boyunca r deki degisiklikler ve yer cekimi kuvvetindeki ardi ardina degisiklikler gozle gorulur bir gel git kuvveti olusturabilir Ornegin Dunya nin yakin ve uzak yuzleri ile Ay arasindaki mesafe farki 6 350 km dir 385 000 km ortalama mesafeye gore kucuk bir fark olsa da bu Ay in Dunya nin okyanuslari uzerinde bir cekim kuvveti olusturmasini ve boylece gelgit olusumuna sebep olur Uzaysal boyutu olan kutlelerEger ilgilenilen kutlelerin uzaysal boyutu varsa teorik olarak noktasal olmaktan ziyade o zaman aralarindaki cekim kuvveti bu kutleleri olusturan kavramsal noktalarin katkilarinin toplanmasiyla hesaplanir Limitte bilesen nokta kutleler sonsuz derecede kuculdukce kuvvetin asagida vektor formu goruluyor iki fiziksel kutlenin boyutlarina oranlarinin integrali gerekir Bu yolla kutlesi kuresel olarak simetrik dagilmis kutle harici kutlelere tum objelerin kutleleri merkezindeki bir nokta etrafinda toplanmis gibi ayni cekim etkisini uygular Bu genellikle kuresel simetrik olmayan kutleler icin gecerli degildir Kuresel simetrik dagilimli bir malzemenin icindeki kutlelerin cekimsel kuvvetini bulmak icin Newton un kabuk teoremi Ing Ingilizce Shell s theorem kullanilabilir Bu teorem bize kutle dagiliminin farkli parcalarinin kutle dagilim merkezinden r0 kadar uzaktaki bir parcayi nasil etkilediklerini aciklar r lt r0 yaricapinda bulunan kutle r0 da sanki kutlenin tamami bu yaricapta bir kuredeki tum kutlenin kutle dagilimi merkezinde toplanmis gibi ayni kuvvete sebep olur yukarida yazildigi gibi r gt r0 yaricapinda bulunan kutle r0 da net cekim kuvveti olusturmaz Ornegin r0 noktasindaki kurenin elementleri tarafindan etkilenen munferit kuvvetler birbirlerini gotururler Ornegin bir sonuc olarak esit dagilan bir kalinlik ve yogunluga sahip olan bir kabuk boyunca net cekim kuvveti sifirdir Vektor formuDunya uzerindeki cekimin makroskopik gorunusu Bir odadaki cekim Dunyanin egriligi bu olcekte goz ardi edilebilir ve kuvvet cizgileri paralele yaklasik ve dunyanin merkezini gosterir sekilde kabul edilebilir Newton un evrensel cekim yasasi hem cekim kuvvetinin buyuklugunu hem de dogrultusunu gosteren bir vektor olarak yazilabilir Bu formulde kalin yazilar vektorleri gostermektedir F12 Gm1m2 r12 2r 12 displaystyle mathbf F 12 G m 1 m 2 over vert mathbf r 12 vert 2 mathbf hat r 12 Burada F12 displaystyle mathbf F 12 1 numarali cismin 2 numaraliya uyguladigi kuvvet G displaystyle G cekim sabiti yercekimi sabiti olan g ile karistirilmamali m1 displaystyle m 1 ve m2 displaystyle m 2 sirasiyla birinci ve ikinci objelerin kutleleri r12 r2 r1 displaystyle vert mathbf r 12 vert vert mathbf r 2 mathbf r 1 vert 1 ve 2 objeleri arasindaki mesafe r 12 def r2 r1 r2 r1 displaystyle mathbf hat r 12 stackrel mathrm def frac mathbf r 2 mathbf r 1 vert mathbf r 2 mathbf r 1 vert ise 1 inci objeden 2 ye olan birim vektordur Esitligin vektorel formunun F nin artik vektorel bir deger olmasi ve sag tarafin uygun birim vektorle carpilmis olmasi haricinde daha onceden verilen skaler formla ayni oldugu gorulebilir Ayrica buradan su da gorulebilir F12 F21 Cekim AlaniCekim alani uzayda verilen herhangi bir noktadaki objeye birim kutle basina uygulanan cekim kuvvetini tanimlayan vektor alanidir Aslinda bu o noktadaki cekim ivmesine esittir Eger birden fazla obje varsa dunya ve ay arasindaki bir roket gibi kullanisli hale gelen bir genellestirmedir Iki obje icin ornegin obje 2 bir roket ve obje 1 de dunya olsun basitce r12 displaystyle mathbf r 12 yerine r displaystyle mathbf r ve m2 displaystyle m 2 yerine m displaystyle m yazabiliriz ve cekim alaninig r displaystyle mathbf g mathbf r asagidaki gibi tanimlayabiliriz g r Gm1 r 2r displaystyle mathbf g mathbf r G m 1 over vert mathbf r vert 2 mathbf hat r Boylece F r mg r displaystyle mathbf F mathbf r m mathbf g mathbf r olur Bu formul alana sebep olan objelerden bagimsizdir Bu alan ivme birimlerine sahiptir ve bu da SI birimlerinde m s2 dir Cekim alanlari ayni zamanda korunumlu alanlardir yani bir pozisyondan oburune cekim tarafindan yapilan is yoldan bagimsizdir Bunun sonucunda potansiyel asagidaki gibi potansiyel V r alani olusur g r V r displaystyle mathbf g mathbf r mathbf nabla V mathbf r Eger m1 noktasal bir kuvvet ise veya homojen dagilmis bir kutle ise kurenin disindaki kuvvet alani g r izotropiktir yonden bagimsizdir ornegin sadece kurenin merkezinden olan r mesafesine baglidir Bu durumda V r Gm1r displaystyle V r G frac m 1 r Newton un teorisinin problemleriNewton un tanimi bircok pratik amac icin yeterli sekilde dogrudur ve bu yuzden genis sekilde kullanilir Boyutsuz degerler f c2 ve v c nin ikisi de kucuk oldugunda kullanilabilir burada f cekimsel potansiyel v incelenen objelerin hizi ve c isik hizidir Ornek olarak Newtonien cekim Dunya Gunes sisteminin dogru bir tanimini saglar cunku Fc2 GMgunesryorungec2 10 8 vyerc 2pryorunge 1 yr c 10 4 displaystyle frac Phi c 2 frac GM mathrm gunes r mathrm yorunge c 2 sim 10 8 quad frac v mathrm yer c frac 2 pi r mathrm yorunge 1 mathrm yr c sim 10 4 burada rorbit dunyanin gunes etrafindaki yorungesinin yaricapidir Boyutsuz degiskenlerden biri buyuk oldugu durumlarda sistemi tanimlamak icin genel gorelilik kullanilmalidir Genel gorelilik kucuk potansiyel ve dusuk hiz sinirlarinda Newton un cekime donusur bu yuzden Newton un cekim yasasi icin siklikla genel goreliligin dusuk cekim limiti denir Teorik kaygilar Cekim arabulucusunu hemen bulma gibi bir ihtimal yoktur Cekimsel kuvvet ile bilinen diger temel kuvvetler arasindaki iliskiyi tanimlamak icin teorisyenler tarafindan yapilan tesebbusler 50 yildir gozle gorulur bir ilerleme kaydedilmis olsa da henuz sonuca ulasmamistir Newton bile aciklanamaz uzaktan etkilesim konusunda kendini yetersiz hissetmistir Newton un teorisi cekimsel kuvvetin ani iletimini gerektirir Genel goreliligin gelistirilmesinden once uzay ve zamanin dogasi ile ilgili yapilan klasik varsayimlar yayilim gecikmesi kararsiz yorungelere sebep olur Gozlemle uyusmazliklar Newton un teorisi gezegenlerin ozellikle Merkur un yorungelerinin gunese en yakin noktalarinin gunberi yalpalamalarini tam olarak aciklamaz Newton un tahminlerle gozlenen yalpalama arasinda diger gezegenlerin cekimsel suruklemelerinden kaynaklanan 43 3600 derecelik 43 arcsecond bir uyumsuzluk bulunmaktadir Newton un teorisi kullanilarak tahmin edilen sapma gozlenenin sadece yarisidir Genel gorelilik ise gozlemlere daha yakindir Cekimsel ve ataletsel kutlelerin tum kutleler icin ayni olmasiyla ilgili gozlenen gercek Newton un sisteminde aciklanamamaktadir Genel gorelilik bunu bir varsayim olarak alir Newton un supheleri Newton kendi anitsal calismasinda cekim yasasini formule edebiliyorken kendi esitliklerinin one surdugu uzaktan etkilesim action at a distance kavrami yuzunden kendini derin sekilde rahatsiz hissediyordu Kendi sozleriyle bu gucun sebebini hicbir zaman tespit edememisti Tum diger durumlarda kutleler uzerine etkiyen cesitli kuvvetlerin sebebini aciklamak icin hareket olgusunu kullanmistir fakat cekimle ilgili durumda cekim kuvvetini ureten hareketi deneysel olarak tanimlayamamisti Dahasi yer uzerindeki bu kuvvetin sebebine gelince bir hipotez onermeyi dahi reddediyordu Filozoflar simdiye kadar cekim kuvvetinin kaynagi icin bosuna doga arastirmasina girismislerdir diye pisman olmustur cunku bircok sebepten dolayi doga olgusunun temeli olan simdiye kadar bilinmeyen sebepler in varligina ikna olmustur Bu temel olgular hala arastirilmaktadir ve hipotezler cok olsa da tanimlayici yanit henuz bulunamamistir Newton un 1713 tarihli ve Principia nin ikinci baskisi olan General Scholium unda Daha henuz cekimle ilgili bu ozelliklerinin sebeplerini olgudan kesfedebilmis degilim ve yalandan hipotez uydurmadim Cekimin varligi ve acikladigim yasalara gore islemesi ve uzaysal kutlelerin yildiz gezegen gibi hesaplamasina yaptigi hizmetler yeterlidir Bir kutle bir baskasini bir vakum icinde baska hicbir seyin arabuluculugu olmadan etkiler etkileri ve kuvvetleri tarafindan ve onlarin icine digerine tasinabilmesi bence buyuk bir garabettir ve bence bu yuzden felsefi malzemelerde dusunmenin bilesen yetisine sahip hic kimse onun icine dusmez Kaynakca Proposition 75 Theorem 35 p 956 I Bernard Cohen and Anne Whitman translators Isaac Newton The Principia Preceded by A Guide to Newton s Principia by I Bernard Cohen University of California Press 1999 ISBN 0 520 08816 6 ISBN 0 520 08817 4 Max Born 1924 Einstein s Theory of Relativity The 1962 Dover edition page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury Venus and Earth The Construction of Modern Science Mechanisms and Mechanics by Richard S Westfall Cambridge University Press 1978
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans