Newton'un hareket kanunları

Newton'un hareket yasaları, bir cisim üzerine etki eden kuvvetler ve cismin yaptığı hareket arasındaki ilişkileri ortaya koyan üç yasadır. İlk kez Isaac Newton tarafından 5 Temmuz 1687 tarihinde yayımlanan Philosophiae Naturalis Principia Mathematica adlı çalışmada ortaya konmuştur. Bu yasalar klasik mekaniğin temelini oluşturmuş, bizzat Newton tarafından fiziksel nesnelerin hareketleri ile ilgili birçok olayın açıklanmasında kullanılmıştır. Newton, çalışmasının üçüncü bölümünde, bu hareket yasalarını ve yine kendi bulduğu evrensel kütleçekim yasasını kullanarak Kepler'in gezegensel hareket yasalarının elde edilebileceğini göstermiştir.

Newton'un birinci ve ikinci yasası (Principia'nın orijinal 1687 baskısından, Latince)

1. Yasa

Eylemsiz referans sistemi adı verilen öyle referans sistemleri seçebiliriz ki, bu sistemde bulunan bir parçacık üzerine bir net kuvvet etki etmiyorsa cismin hızında herhangi bir değişiklik olmaz. Bu yasa genellikle şu şekilde basitleştirilir: “Bir cisim üzerine dengelenmemiş bir dış kuvvet etki etmedikçe, cisim hareket durumunu (durağanlık veya sabit hızlı hareket) korur.”

2. Yasa

Eylemsiz bir referans sisteminde, bir parçacık üzerindeki net kuvvet onun çizgisel momentumunun zaman ile değişimi ile orantılıdır:

${\displaystyle F=m\cdot {\frac {dv}{dt}}}$

Momentum (mv), kütle ile hızın çarpımına eşittir. Kuvvet ve momentum vektörel nicelikler olduğundan, net kuvvet cisim üzerine etki eden tüm kuvvetlerin vektörel toplamı ile bulunur. Bu yasa sıklıkla şu şekilde ifade edilir: “F=ma: Bir cisim üzerindeki net kuvvet, cismin kütlesi ile ivmesinin çarpımına eşittir.”

3. Yasa

Bir cisme, bir kuvvet etki ediyorsa; cisimden kuvvete doğru eşit büyüklükte ve zıt yönde bir tepki kuvveti oluşur. Burada dikkat edilmesi gereken bu kuvvetlerin aynı doğrultu üzerinde olduğudur. Bu yasa çoğu zaman şu cümle ile basitleştirilebilir: “Her etkiye karşılık eşit büyüklükte ve zıt bir tepki vardır.”

Bu yasalara getirilen çeşitli yorumlar vardır. En genel olan yorumda kütle, ivme ve (en önemlisi) kuvvetin önceden tanımlanmış olduğu varsayılmaktadır. Ancak Newton'ın birinci ve ikinci yasasının aslında kuvvetin ve kütlenin tanımı olduğuna dair yorumlar da mevcuttur.

Dikkat edilirse ikinci yasa ancak gözlem bir eylemsiz referans sisteminden yapıldığında geçerlidir. Eylemsiz referans sistemi birinci yasada tanımlanmış olduğundan ikinci yasayı kullanarak birinci yasanın ispatını aramak mantıksal bir yanılgı olacaktır.

Işık hızına yaklaşan hızlarda Newton yasaları fiziksel olayları açıklamakta yetersiz kalmakta, bu nedenle geçerliliklerini yitirmektedirler. Işık hızlarına yakın hızlarda cisimlerin hareketi incelenirken Albert Einstein'ın geliştirdiği özel görelilik teorisi dikkate alınmalıdır.

Newton'un hareket kanunları

Newton'un birinci yasası: Eylemsizlik yasası

“	Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.	„

“	Yasa I: Tüm cisimler bir kuvvet etkisi tarafından durumunu değiştirmeye zorlanmadıkça düzgün doğrusal hareketini veya durağanlığını korur.	„

Basitleştirilmiş bir şekilde, bir cisim üzerindeki net kuvvet, o cisim üzerine etki eden tüm kuvvetlerin vektörel toplamıdır. Bu toplam sıfır ise, Newton'ın birinci yasası cismin hareket durumunun değişmeyeceğini söyler. Aslında burada iki durum oluşur:

• Hareket etmeyen bir cisim, üzerine bir net kuvvet etki edinceye dek hareket etmeyecektir.
• Hareketli bir cisim, üzerine net bir kuvvet etki etmedikçe hızını değiştirmeyecektir (ivmelenmeyecektir).

Birinci durum çoğu kişi tarafından açıkça anlaşılabilir olmasına rağmen, ikinci durumu anlamak için üzerinde biraz düşünmek gereklidir çünkü gündelik yaşantımızda hareketini sürekli olarak sürdüren cisimleri pek görmeyiz (göksel hareketler hariç). Bir kalemi masa üzerinde kaydırırsak, hareketini sonsuza dek sürdürmeyecek, yavaşlayıp en sonunda duracaktır. Kalemin hızı değişmiştir ve Newton'ın yasalarına göre böyle bir hız değişikliği ancak cisim üzerine bir net kuvvet etki etmesi sonucunda oluşabilir. Bu kuvvet kalem ve masa arasında, kalemin hareketinin tersi yöndeki sürtünme kuvvetidir ve cismin yavaşlamasına neden olmaktadır. Böyle bir kuvvetin yokluğunda kalemin hızı azalmayacak, hareketini sürdürmeye devam edecektir. Sürtünme kuvvetinin az olduğu durumlara bir örnek olarak bir hava hokeyi masası veya buz pateni pisti verilebilir.

Yasanın doğruluğunu mükemmel bir şekilde gösteren deneyler sürtünmenin her deneyde kaçınılmaz olarak ortaya çıktığı için yapılamamaktadır. Öyle ki dış uzayda bile engellenemeyen kütleçekimsel kuvvetler böylesi mükemmel bir deneyin yapılmasını engellemektedir. Ancak yine de yasa, bir nesnenin hareket durumundaki değişikliğin temel nedenlerini vurgulamakta işe yaramaktadır.

Newton'ın birinci yasası eylemsizlik yasası olarak da bilinmektedir ve sıklıkla "sıfır net kuvvet, sıfır ivmelenmeye karşılık gelir." şeklinde açıklanır. Ancak bu açıklama fazla basitleştirilmiştir. Newton tarafından formüle edildiği üzere, birinci yasa ikinci yasanın özel bir hali olmaktan daha fazla şey içerir. Newton iyi bir nedenle yasalarını hiyerarşik bir sıralamada düzenlemiştir. Öyle ki birinci yasa, diğer yasaların uygulanabilir olduğu "eylemsiz referans çerçeveleri" olarak adlandırılan referans çerçevelerini tanımlar. Yasaların niçin eylemsiz referans sistemleri ile sınırlı olduğunu anlamak için ivmeli hareket eden bir cisim (örneğin pistte kalkış için hızlanmakta olan bir uçak) içinde duran bir topu göz önüne alın. Uçak içinde bulunan herhangi bir kişinin bakış açısından (ya da teknik bir deyiş ile "uçağın referans çerçevesinden") uçak ileri doğru ivmelendikçe, top geriye doğru hareket ediyormuş gibi görünecektir (bu etki uçak ivmelenirken sizi koltuğunuza bastıran etki ile aynıdır). Uçak içindeki yolcuların bakış açısından topu hareket ettirecek hiçbir kuvvet bulunmamasına rağmen topun bu hareketi, Newton'ın ikinci yasası ile çelişir gibi görünmektedir. Gerçekte ise ikinci yasa ile ilgili bir çelişki yoktur çünkü Newton'ın ikinci yasası böyle bir durum için uygulanabilir değildir: İkinci yasa ancak topun üzerine bir kuvvet etki etmediğinde onun sabit kalacağı eylemsiz referans sistemlerinde (birinci yasada tanımlanan) geçerlidir. Bu durumda "uçak referans sistemi" bir eylemsiz referans sistemi değildir. Görüldüğü üzere, tüm yasalar her durumda uygulanabilir olmadığından, çeşitli yasaların çeşitli durumlara uygulanabilir olup olmadıkları konusu önem taşımaktadır. Özetlemek gerekirse:

Eylemsiz referans sistemleri olarak adlandırılan öyle referans sistemleri vardır ki bu sistemlerde bulunan gözlemciler için üzerine herhangi bir kuvvet etki etmeyen tüm cisimler hareket durumunu korur.

Eylemsizlik yasasının tarihi

Newton'ın birinci yasası Galileo tarafından daha önce açıklanan eylemsizlik yasasının bir yeniden ifadesidir. Bu görüş, tüm cisimlerin evrende doğal bir yerinin olduğunu söyleyen Aristocu görüşten farklıdır. Aristo, kayalar gibi ağır cisimlerin Dünya üzerinde, duman gibi hafif nesnelerin gökyüzünde, yıldızların ise cennette durma isteklerinin olduğuna inanıyordu. Buna rağmen Aristo'nun ve Galileo'nun fikirleri arasındaki temel fark Galileo'nun bir cisim üzerine etki eden kuvvetin cismin hızını değil ivmesini belirliyor olduğunu söylemesidir. Yine Aristo'dan farklı olarak Galileo bu söylemini inançlarına değil, deney ve gözleme dayalı olarak ortaya koymuştur. Bu anlayış Newton'ın, birinci yasasını (kuvvet yoksa, ivme yoktur) oluşturmasında yol göstermiş ve üzerine kuvvet etkimeyen cisimlerin hızlarını koruyacağı görüşünü ortaya çıkarmıştır.

Görünüşe göre eylemsizlik yasası birbirinden bağımsız olarak birkaç doğa filozofu tarafından keşfedilmiştir. Hareketin eylemsizliği MÖ 3. yüzyılda Çin filozofu tarafından, MS. 11. yüzyılda İslam bilginleri İbn-i Heysem ve İbn-i Sina tarafından açıklanmıştır. 17. yüzyılda yaşamış olan filozof René Descartes yasayı formüle etmiştir ancak onu doğrulamak için hiçbir deney yapmamıştır.

Newton'un ikinci yasası: Dinamiğin temel prensibi

“	Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur..	„

“	Yasa II: Bir cismin momentumundaki değişim, cisim üzerine uygulanan itme ile orantılıdır ve itmenin uygulandığı düz doğru boyunca meydana gelir.	„

Newton'ın Latince kitabından Motte'nin 1729 yılında yaptığı çeviride ikinci hareket yasası aşağıdaki gibi ifade edilmiştir:

“	Hareketin değişimi, uygulanan hareket ettirici kuvvet ile doğru orantılıdır ve kuvvetin uygulandığı düz çizginin doğrultusundadır. -Bir kuvvet ister tümüyle bir seferde, isterse de kademeli ve art arda uygulansın, eğer bir hareket oluşturuyorsa, bu kuvvetin iki katı büyüklüğe sahip başka bir kuvvet hareketi ikiye, üç katı büyüklüğündeki bir kuvvet hareketi üçe katlayacaktır. Ve bu hareket (uygulanan kuvvet ile her zaman aynı doğrultuda), eğer cisim daha önceden hareket halinde ise, önceki hareket ile aynı doğrultuda olması durumunda önceki hareket ile toplanır, önceki hareket ile zıt doğrultuda olması durumunda önceki hareketten çıkartılır. Eğer önceki hareketin doğrultusu ile uygulanan kuvvet etkisi ile oluşturulan yeni hareketin doğrultusu birbirinden farklı ise cismin sonuç olarak hareketi, doğrultuları farklı bu iki hareketin bileşimi şeklinde olacaktır.	„

Modern sembolik gösterim ile Newton'ın ikinci yasası bir vektörel diferansiyel denklem şeklinde yazılabilir:

${\displaystyle \mathbf {F} _{\text{net}}={\mathrm {d} (m\mathbf {v} ) \over \mathrm {d} t}}$

Burada F kuvvet, m kütle, v hız vektörü ve t zamandır.

Kütle ve hızın çarpımı cismin momentumu olarak tanımlanmıştır (Newton tarafından bu çarpım "hareket miktarı" olarak adlandırılmıştır). Bu eşitlik sabit kütleye sahip sistemler için kuvvet ve momentum arasındaki fiziksel ilişkiyi ifade eder. Eşitlik sıfır net kuvvet etkisi altındaki bir sistemin momentumunun zamanla değişmeyeceğini söyler. Buna rağmen böyle bir durumdaki sisteme giren veya çıkan herhangi bir miktardaki kütle, bir dış kuvvet etkisi sonucu olmaksızın sistemin momentumunu değiştirecektir ki bu durum ikinci yasaya aykırıdır. Böyle durumlarda bu eşitlik geçersizdir.

Bakınız açık sistemler.

Bu eşitliğin eylemsizlik yasası ile uyumlu olması açısından belirtilmelidir ki, momentumun büyüklüğü değişmeksizin, sadece yönü değişiyorsa, momentumun zamana göre türevi sıfırdan farklı olmalıdır.

Sistemin kütlesi sabit olduğundan bu diferansiyel denklem daha basit ve bilinen bir formda yazılabilir:

${\displaystyle \mathbf {F} =m\mathbf {a} }$

Bu eşitlikte

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}$

ivmeyi belirtmektedir.

F=ma eşitliğini sözlü olarak "bir cismin ivmesi, üzerine uygulanan kuvvet ile doğru, cismin kütlesi ile ters orantılıdır." şeklinde ifade edebiliriz. Genel olarak, ışık hızına göre düşük olan hızlarda, momentum ve hız arasındaki ilişki yaklaşık olarak doğrusaldır. Gündelik yaşamımızda deneyimlediğimiz neredeyse tüm hızlar bu kategoridedir. Buna rağmen, ışık hızına yaklaşan hızlarda momentum-hız arasındaki bu doğrusal yaklaşım giderek artan biçimde hatalı olmaktadır ve özel görelilik kuramının kullanımına ihtiyaç duyulmaktadır.

İtme

İtme terimi ikinci yasa ile yakından ilişkilidir ve tarihsel olarak yasanın orijinal anlamına daha yakındır. İtme aşağıdaki gibi tanımlanmaktadır:

Bir itme, bir F kuvvetinin Δt zaman aralığı boyunca etkimesi sonucu oluşur ve ${\displaystyle \int _{\Delta t}\mathbf {F} \,\mathrm {d} t}$ ifadesi ile gösterilir.

Newton tarafından "İtme" kavramı hareket ettirici kuvvet olarak, "Momentum" kavramı ise hareket olarak ifade edilmiştir. Sonuç olarak ikinci yasanın tarihsel yaklaşım ile itme ve momentum değişimi arasındaki ilişkiyi böyle açıkladığı söylenebilir. Dolayısıyla ikinci yasa orijinaline uygun şekilde matematiksel olarak sonlu farklar şeklinde ifade edilebilir:

${\displaystyle \mathbf {I} =\Delta \mathbf {p} =m\Delta \mathbf {v} }$

Burada I itme, Δp momentumdaki değişim, m kütle ve Δv hızdaki değişimdir.

Çarpışmaların analizinde itme kavramı kullanılmaktadır.

Değişken kütleli sistemler

Yaktığı yakıtı püskürterek yol alan ve bir roket gibi değişken kütleli sistemler, kapalı sistem değildirler. Bu tip sistemleri incelerken ikinci yasadaki kütleyi doğrudan zamanın bir fonksiyonu olarak alamayız. Bunun nedeni, Kleppner ve Kolenkow'un An Introduction to Mechanics (Mekaniğe giriş) kitabında ve diğer modern metinlerde verildiği üzere, Newton'ın ikinci yasasının temel olarak noktasal parçacıklara uygulanabilmesidir. Klasik mekanikte parçacıklar, tanımları gereği sabit kütleye sahiptirler. İyi tanımlanmış parçacık sistemleri için Newton yasaları, sistemde bulunan tüm parçacıklar üzerinden toplam alınarak genişletilebilir:

${\displaystyle \mathbf {F} _{\mathrm {net} }=M\mathbf {a} _{\mathrm {km} }}$

Burada F_net sistem üzerindeki toplam dış kuvvet, M sistemin toplam kütlesi ve a_km sistemin kütle merkezinin ivmelenmesidir.

Bir roket, su sızdıran bir kova veya ucu salınan şişirilmiş bir balon gibi değişken kütleli sistemleri parçacık sistemleri olarak ele alıp işlem yapmak genellikle çok zordur, bu nedenle bu tip sistemler için Newton'ın ikinci yasası doğrudan uygulanamaz. Bunun yerine m kütlesi zamanla artan veya azalan bir cismin genel hareket denklemi, ikinci yasanın, sisteme giren veya sistemden ayrılan kütle tarafından taşınan momentumu ifade eden bir terimin eklenerek yeniden düzenlenmesiyle elde edilir:

${\displaystyle \mathbf {F} +\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}$

Burada u sistemden kaçan veya sisteme giren kütlenin, sistemin kütle merkezine göre hızıdır. Kimi standartlara göre, denklemin sağ tarafında "tepki" (İng. thrust) olarak adlandırılan u dm/dt ifadesi, kuvvet (değişen kütle nedeniyle cisim üzerine uygulanan kuvvet, roket egzozu gibi) olarak tanımlanır ve F niceliğine dahil edilir. İvmenin tanımının da yerine koyulması ile eşitlik,

${\displaystyle \mathbf {F} =m\mathbf {a} .}$

halini alır.

Görelilik

1. Özel göreliliği göz önüne alarak, bileşke kuvvet yasası ivme cinsinden aşağıdaki gibi ifade edilebilir:

${\displaystyle {\begin{aligned}\mathbf {F} &={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}\\&=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+{\frac {\mathrm {d} m}{\mathrm {d} t}}\mathbf {v} \\&=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+{\frac {1}{c^{2}}}{\frac {\mathrm {d} E}{\mathrm {d} t}}\mathbf {v} \\&=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+{\frac {\mathbf {F} \cdot \mathbf {v} }{c^{2}}}\mathbf {v} \end{aligned}}}$

Bu eşitliğin elde edilmesinde enerjinin meşhur 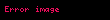${\displaystyle E=mc^{2}}$ ifadesi kullanılmıştır. (${\displaystyle dm/dt=(1/c^{2})dE/dt}$) Dikkat edilmesi gereken nokta bu eşitliğin yaklaşık bir eşitlik olduğudur. (Bir cismin toplam enerjisi ${\displaystyle E=\gamma mc^{2}}$ olarak ifade edilir. ${\displaystyle \gamma }$ Lorentz faktörü olup ışık hızından çok daha yavaş hareket eden cisimler için yaklaşık olarak birdir.) Aşağıdaki eşitlik bir kuvvet tarafından birim zamanda yapılan işi ifade eder:

${\displaystyle {\frac {\mathrm {d} E}{\mathrm {d} t}}=\mathbf {F} \cdot \mathbf {v} }$

Burada F·v, vektörel skaler çarpımdır.

Bu denklem genişletilmiş bir kuvvet yasası için tekrar düzenlenebilir:

${\displaystyle m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=\mathbf {F} -{\frac {\mathbf {F} \cdot \mathbf {v} }{c^{2}}}\mathbf {v} {\text{,}}}$

Bu eşitlik momentum değişiminin kuvvet doğrultusunda olmasına rağmen, bir kütlenin ivmesinin genel olarak kuvvetin doğrultusunda olmadığını göstermektedir. Buna rağmen eğer hareket eden bir cismin hızı ışık hızından çok düşükse, yukarıdaki eşitlik bilindik F=ma eşitliğine dönüşür.

Açık sistemler

Kütlesi değişen sistemler kapalı sistemler değildir. Örneğin yaktığı yakıtları dışarı püskürterek hareket eden bir roket için, Newton'ın ikinci yasasında kütleyi doğrudan zamanın bir fonksiyonu olarak alarak işe koyulamayız. Bunun nedeni, Kleppner ve Kolenkow 'un An Introduction to Mechanics adlı kitabında ve diğer modern metinlerde verildiği üzere Newton'ın ikinci yasasının temel olarak sadece parçacıklara uygulanabilir olmasıdır. Klasik mekanikte parçacıklar sabit kütleli olarak tanımlanır. Parçacıklar iyi tanımlanmış sistemleri oluşturduğu takdirde, Newton'ın yasası tüm parçacıklar üzerinden bir toplam alınarak genişletilebilir. Bu durumda sistemi oluşturan tüm parçacıklar kütle merkezinde bulunan, kütlesi tüm parçacıkların kütleleri toplamına eşit bir tek parçacıkmış gibi ele alınabilir. İkinci yasayı böylesi genişletilmiş cisimlere uygularken, yasa tamamıyla cismin iyi tanımlanmış parçacıklardan meydana geldiğini kabul eder. Buna rağmen bir roket gibi değişken kütleli sistemler belli sayıdaki parçacıklardan oluşmaz. Böyle sistemler iyi tanımlanmış sistemler değildir. Bu nedenle böyle sistemlere Newton'ın ikinci yasasını doğrudan uygulayamayız. Böyle durumlarda F = dp/dt eşitliğinin dikkatsizce kullanılması yanlış sonuçlar verecektir. Buna rağmen, momentumun korunumunu tüm sisteme uyguladığımızda (örneğin roket ve yakıtı) elde ettiğimiz sonuçlar kesinlikle doğru olacaktır.

Son cümlede kullanılan tüm sistem ifadesi genişletilmiş, sabit kütleli ve tüm parçacıkları belirli bir sisteme karşılık gelir. Bu durum, F = dp/dt ifadesinin sadece sabit kütleli sistemler için doğru olduğu anlamına gelir. Buna rağmen yasa F = ma şeklinde ifade edildiğinde, bileşke kuvvet sisteme giren veya çıkan kütlenin ikisini de içerecek şekilde alındığında, kütlenin değişimine aldırmaksızın herhangi bir parçacığın veya sistemin hareketini doğrulukla açıklar.

Newton'un üçüncü yasası: Etki-tepki yasası

“	Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi.	„

“	Yasa III: Her kuvvete karşılık, her zaman eşit ve ters bir tepki kuvveti vardır: veya iki cismin birbirine uyguladığı kuvvetler her zaman eşit ve zıt yönelimlidirler.	„

Newton'ın üçüncü yasası. Patencilerin birbirine uyguladıkları kuvvetler eşit büyüklükte ve zıt yönlüdürler.

Daha doğrudan bir çeviri şu şekilde yapılabilir:

“	YASA III: Her etki için ona eşit ve zıt yönlü bir tepki vardır: veya iki cismin birbirine uyguladıkları karşılıklı etkiler eşit ve karşıt taraflara yönelimlidirler. — Karşı tarafı iten veya çeken her ne ise, aynı ölçüde karşı taraf tarafından itilir veya çekilir. Eğer parmağınızla bir taşı itiyorsanız, aynı zamanda parmağınız da taş tarafından itilecektir. Eğer bir at, ip ile bağlanmış bir taşı çekiyorsa, at da eşit olarak taş tarafından geriye doğru çekilecektir: gerilmiş haldeki ip gevşemek için, taşı ata çektiği ölçüde, atı da taşa doğru çekecektir ve birinin ilerlemesini engellediği kadar diğerinin ilerlemesini de engelleyecektir. Eğer bir cisim diğerine çarparsa ve uyguladığı kuvvet diğerinin hareketini değiştirse, kendi hareketi de (ortak baskının eşitliği nedeniyle) aynı miktarda ve karşıt yönde bir değişime uğrayacaktır. Eğer cisimler başka engeller tarafından engellenmiyorsa, bu etkiler tarafından oluşturulan değişimler eşittir, ancak bu eşit miktarda değişen bu nicelikler cisimlerin hızları değil, hareketleridir. Hareketler eşit miktarda değiştiğinden, cisimlerin ters taraflara doğru meydana gelen hız değişimleri birbirleri ile ters orantılıdır. Bu yasa sonraki notlarda ispatlanacağı üzere çekim etkilerinde de yer alır.	„

Alışılmış olduğu üzere Newton yukarıdaki çeviride momentumdan hareket olarak bahsetmiş, "hız" ile "hareket" arasındaki farka dikkat çekmiştir.

Newton'ın üçüncü yasası, tüm kuvvetlerin etkileşimler olduğunu söyler -yani tek yönlü kuvvet diye bir şey yoktur. Eğer bir A cismi, bir B cismi üzerine bir kuvvet uyguluyorsa B cismi de aynı anda A üzerine aynı büyüklükte bir kuvvet uygular; öyle ki uygulanan bu kuvvetler aynı doğru üzerinde yer alır. Şekilden görüleceği üzere, patenciler birbirlerine büyüklükleri aynı fakat yönleri ters olan kuvvetler uygular. Uygulanan kuvvetler eşit olmasına rağmen ivmelenmeler eşit değildir: Newton'ın ikinci yasasına göre daha zayıf olan patenci daha büyük bir ivme kazanacaktır. Burada dikkat edilmesi gereken konu etki/tepki çiftinin farklı nesneler üzerine etkidiği ve birbirini yok etmediğidir. Newton'ın üçüncü yasasındaki iki kuvvet aynı tiptedir, örneğin, eğer yol, ivmelenen bir araba lastiği üzerinde ileri yönlü bir sürtünme kuvveti uyguluyorsa (ki bu kuvvet, arabanın hareket etmesini sağlayan kuvvettir), bu sürtünme kuvveti Newton'ın üçüncü yasasına göre aynı zamanda lastikleri yol üzerinde geri iter.

Newton üçüncü yasayı, momentumun korunumu yasasını türetmek için kullanmıştır; buna rağmen daha derin bir bakış açısı ile momentumun korunumu, daha temel bir fikirdir (Galileo) dönüşümlerinden Noether teoremi aracılığıyla ispatlanır) ve Newton'ın üçüncü yasasının geçerli olmadığı durumlarda da geçerliliğini korur (örneğin parçacıkların momentum taşıdığı gibi kuvvet alanlarının da momentum taşıması durumunda veya kuantum mekaniğinde).

Önemi ve geçerlilik erimi

Newton yasaları 200 yıldır çeşitli deneyler ve gözlemler ile doğrulanmıştır ve gündelik yaşantımızdaki hızlar ve ölçekler için mükemmel birer yaklaşımdırlar. Newton'un hareket yasaları, yine onun bulduğu evrensel kütleçekim yasası ve kalkülüs'ün matematiksel yöntemleri ile birlikte, ilk kez geniş çaptaki fiziksel olaylar için niceliksel bir açıklama sağlamıştır.

Bu üç yasa, gündelik koşullarda makroskopik cisimlerin hareketi için iyi bir yaklaşıklık ile geçerlidirler. Buna rağmen, çok küçük ölçeklerde, çok yüksek hızlarda veya çok güçlü kütleçekimsel alanların varlığında geçerliliklerini yitirirler. Bu nedenle yasalar, bir yarı iletkendeki elektrik iletimi, maddelerin optik özellikleri, relavite hesaba katılmadan düzenlenen GPS sistemlerindeki hatalar ve süper iletkenlik gibi olayları açıklamakta kullanılamazlar. Bu tip olayların açıklanabilmesi, Genel Görelilik ve Relativistik Kuantum Mekaniği gibi daha karmaşık fiziksel teorileri gerektirir.

Kuantum mekaniğinde kuvvet, momentum veya konum gibi kavramlar, bir kuantum durumu üzerine işlem yapan, doğrusal operatörler ile tanımlanır. Işığın hızından çok düşük olan hızlarda, bu operatörler Newton yasalarına indirgenir. Işık hızına yaklaşık hızlarda, bir cisim için kuvvetin o cismin momentumunun zamana göre türevi olduğunu söyleyen ikinci yasa orijinal halini (F = d (p) / dt) korusa da, ikinci yasanın bazı yeni sürümleri (yukarıdaki sabit kütle yaklaşımı gibi) geçerliliklerini koruyamamaktadırlar.

Kaynakça

1. ^ Bakınız Principia online Andrew Motte'nin İngilizce Çevirisi
2. ^ "Principia 'nın Andrew Motte çevirisi (1687) Aksiyomlar veya Hareket Yasaları". 22 Aralık 2008 tarihinde kaynağından . Erişim tarihi: 28 Ocak 2009. 
3. ^ Bakınız Prof. Dr. Emine Rızaoğlu, Dr. Naci Sünel - Klasik mekanik
4. ^ İkinci yasada, momentumun relativistik ifadesi kullanılmalıdır ve üçüncü yasa, birbirinden uzak cisimler arasındaki etkileşimin bir anda değil sonlu bir hızda oluşacağı şekilde genişletilmelidir.

Dış bağlantılar

• (Türkçe) onlinefizik - Newton'ın hareket kanunları 18 Kasım 2014 tarihinde Wayback Machine sitesinde .
• (İngilizce) NASA - Newton'ın hareket yasaları 10 Aralık 2008 tarihinde Wayback Machine sitesinde .
• (İngilizce) Yerçekimi - Çocuklar için Newton yasaları19 Mayıs 2008 tarihinde Wayback Machine sitesinde .
• (İngilizce) Newton'ın birinci yasası için benzetim27 Mart 2008 tarihinde Wayback Machine sitesinde .