Pearson ki-kare testi nicel veya nitel değişkenler arasında bağımlılık olup olmadığının, örnek sonuçlarının belirli bir teorik olasılık dağılımına uygun olup olmadığının, iki veya daha fazla örneğin aynı anakütleden gelip gelmediğinin, ikiden fazla anakütle oranının birbirine eşit olup olmadığının ve çeşitli anakütle oranlarının belirli değere eşit olup olmadığının araştırılmasında kullanılır. İstatistik biliminin çıkarımsal istatistik bölümünde ele alınan iki-değişirli analizlerinden olan ve ki-kare dağılımı'nı esas olarak kullanan ki-kare testlerinden en çok kullanılanıdır. İngiliz istatistikçi olan tarafından 1900'da ortaya çıkartılmıştır.
Bağımsızlık testi
Pearson ki-kare testi yönteminin pratik bir problem çözülmesinde kullanılması şu basamaklar kullanılarak yapılır.
1. Araştırma konusu:
Pearson'un ki kare testi her biri iki kategorili olan iki isimsel ölçekle ölçülebilen rassal değişken arasındaki bağımsızlık veya bağımlılık ilişkisinin incelenmesi için kullanılır. Bir iki isimsel ölçekle ölçülebilen rassal değişken
"satır değişkeni" :
kategorili ve
"sütun segiskeni" :
kategorili
.
Araştırma konusu genellikle X ile Y değişkenlerinin birbirinden istatistiksel olarak bağımsız olduğudur. Buna başlıca neden Pearson'ın ki kare yeştinin "bağımlılık" konusunda çok zayıf sonuç vermesidir.
2. Hipotezler:
Pearson'un ki kare test için hipotezler şöyle ifade edilir:
- H0</sub) "sıfır hipotez" : iki kategorili olan iki isimsel ölçekle ölçülebilen rassal değişken birbirinden istatistiksel olarak bağımsızdır.
- H1 "alternatif hipotez": iki kategorili olan isimsel ölçekle ölçülen iki rassal değişken birbirinden istatistiksel olarak bağımsız değildir.
Bu hipotezlerden açıkça görülmektedir ki sınanma için kullanılan hipotez anakütle parametreler değerleri hakkında değildir ve bir istatistiksel nitelik hakkındadır. Böylece Pearson ki-kare testi bir parametrik olmayan istatistik örneğidir. Bunun yanında, dikkat edilmelidir ki alternatif hipotezin bir "negatif" cümle olarak ifade edilmektedir. yani "istatistiksel olarak bağımsız değildir" ifadesi. Bu ifade pozitif vir cümle yani alternatif hipotezde "iki rassal değişken istatistiksel olarak bağımlıdır." dememektedir. Yapılan çıkarımsal test analizi sonuncu "sıfır hipotez" reddedilirse iki değişkeninin ne kadar birbirine bağımlı olduğu bulunmaz; bağımlılık derecesi çok küçük olması mümkündür.
3. Veri toplanması, her hücresi için "gözlemlenen değerler" bulunan ve marjinal toplamlar:
Pearson ki kare testi "iki-değişirli" istatistiksel analize örnektir; yani her bir "vaka" için iki değişir hakkında veri elde edilir. Değişir için sadece X ve Y olan iki-isimsel ölçekli değişken hakkında cevap olabilir. Örneğin; bir ankete verilen tek kişi cevabı "tek vaka"dır ve araştırmada bu ankete bulunan iki soruya, yani 2 değişire, araştırmacı ilgisi çekilmektedir. Her iki değişir de isimsel ölçekli kategorik değerler alabilir. İki-değişir kategorili gözlem özetlenmesi bir "kontenjans tablosu" halinde olur ve Pearson ki-kare testi için pratikte kullanılan veriler bu karşılıklı olarak sınıflandırılmış iki değişirli "kontenjans tablosu" halindedir.
Kontenjans tablosu verileri şu tip tabloda özetler:
 değişiri değişiri | Satır Toplamı Σ | ||||||
 değişiri değişiri | 1 | 2 | … | k | … | c | nj. |
| 1 | O11 | O12 | ... | O1k | ... | O1r | O1. |
| 2 | O21 | O22 | … | O2k | … | O2c | n2. |
| … | … | … | … | … | … | … | … |
| j | … | … | … | Ojk | … | … | nj. |
| … | … | … | … | … | … | … | … |
| r | Or1 | Or2 | … | Ork | … | Orc | nc. |
| Sütun toplamı Σ | n.1 | n.2 | … | n.k | … | n.c | n |
Bu tabloda bulunan rxc adet 


Satır toplamları hepsinin toplamı ve sütün toplamları hepsinin toplamı toplam gözlem sayısına, yani örneklem büyüklüğü olan n değerine eşittir.
4. Teorik "beklenen değerler":
Her bir hücre üçün bur "beklenen değer" yani Ejk l-1,...r ve k=1,...c bulunur. Bu "beklenen değer" olasılık teoeiasinde bulunan iki bağımsız rassal değişken olan A ve B için "çarpım savı"na dayanır. Bu "bağımsız iki rassal değişken için çarpım savı" şöyle ifade edilir:
Bu savı kullanarak ve olasılığın asımtotik olarak "relatif çokluluk"'a eşit olduğu kabul edilip, eğer X ve Y değişirleri sıfır hipoteze uygun olarak bağımsızlarsa, her bir (jk) hücresi için olasılık şöyle ifade edilebilir:
Bu olasılık ifadesinin her iki tarafını da 
5: Hesaplanan ki-kare değeri. Serbestlik derecesi
Hesaplanan ki-kare değeri
Serbestlik derecesi : 
6. Anlamlılık seviyesi ve bu seviye için teorik test istatistik ki-kare değeri
Anlamlılık seviyesi ve p-değeri.

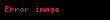


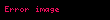

7. Test sonucu ve araştırma konusu
Uygunluk iyiliği testi
"Tekdüze ayrık dağılım'a uygunluk", binom dağılım'a uygunluk", 'a uygunluk" ve eğer normal değerler sınıflandırılıp sınıf ortalaması kategori değeri gibi kullanılırsa "normal dağılım'a uygunluk" testleri olabilirler.
Ayrık tekdüze dağılımına uygunluk testi
Bu tip problemde 

"Sıfır hipotez" bu veri dağılımının teorik olarak 'ina uyacağıdır ve bu dağılıma uymayacağıdır. Bu çok basit sıfır hipotezleri ve teorik olarak her bir hücrenin birbirine eşit sayıda "beklenen değer" alacağını önerir. Tekrar dikkat edilmelidir ki "ki-kare dağılım iyiliği" testi de (diğer Pearson ki-kare testi" gibi) eğer sıfır hipotez reddelerse "zayıf" sonuç verir; yani eldeki veriler "ayrık tekdüze dağılım"'a uymaz ama hangi dağılım uyduğu bu test ile açığa çıkmaz.
Teorik "ayrık tekdüze dağılımı"'na göre rassal değişkende her bir veri kategorisi aynı olasılık gösterir. Bu nedenle N tane veri için her bir i kategorisi için aynı değer taşıyan "beklenen değer", E, yani
olarak hesaplanır.
"Hesaplanan ki-kare değeri" her hücre için "gözlemlenen değer" eksi "beklenen değer" farkının karesinin "beklenen değer"'e bölünmesinin tüm hücreler için toplanmasıdır: Yani
Test istatistiğinin hesaplanması
Uygunluk iyiliği sınaması için test istatistiği su formüle göre hesaplanmış:
Bu formülde
= Pearson'un kümülatif test istatistiği olup, bu "hesaplanmış
" değeri asimtotik olarak bir 'na yakınlaşmaktadır.
= gözlenen cokluluk değeri;
= sıfır hipotez önerisinin gerçek olduğu kabul edilerek bir teorik beklenmekte olan çokluluk değerdir ;
= tabloda bulunan hücre sayısı

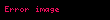 " degerlerini dikey Y-ekseni ise P-degerleridir.
" degerlerini dikey Y-ekseni ise P-degerleridir.Ayrıca bakınız
Kaynakça
- ^ Karl Pearson (1900). "On the criterion that a given system of deviations from the probable ın the case of a correlated system of variables is such that it can be reasonably supposed to have arısen from random sampling". Philosophical Magazine, Series 5. 50 (302). ss. 157-175. doi:10.1080/14786440009463897.
Dış bağlantılar
- Eric W. Weisstein, Chi-Squared Test (MathWorld)
- Greenwood, P.E., Nıkulin, M.S.(1996). A guide to chi-squared testing, New York: J.Wiley, .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Pearson ki kare testi nicel veya nitel degiskenler arasinda bagimlilik olup olmadiginin ornek sonuclarinin belirli bir teorik olasilik dagilimina uygun olup olmadiginin iki veya daha fazla ornegin ayni anakutleden gelip gelmediginin ikiden fazla anakutle oraninin birbirine esit olup olmadiginin ve cesitli anakutle oranlarinin belirli degere esit olup olmadiginin arastirilmasinda kullanilir Istatistik biliminin cikarimsal istatistik bolumunde ele alinan iki degisirli analizlerinden olan ve ki kare dagilimi ni esas olarak kullanan ki kare testlerinden en cok kullanilanidir Ingiliz istatistikci olan tarafindan 1900 da ortaya cikartilmistir Bagimsizlik testiPearson ki kare testi yonteminin pratik bir problem cozulmesinde kullanilmasi su basamaklar kullanilarak yapilir 1 Arastirma konusu Pearson un ki kare testi her biri iki kategorili olan iki isimsel olcekle olculebilen rassal degisken arasindaki bagimsizlik veya bagimlilik iliskisinin incelenmesi icin kullanilir Bir iki isimsel olcekle olculebilen rassal degisken X displaystyle X satir degiskeni r displaystyle r kategorili ve j displaystyle j j 1 r displaystyle j 1 dotsc r Y displaystyle Y sutun segiskeni c displaystyle c kategorili k displaystyle k k 1 c displaystyle k 1 dotsc c Arastirma konusu genellikle X ile Y degiskenlerinin birbirinden istatistiksel olarak bagimsiz oldugudur Buna baslica neden Pearson in ki kare yestinin bagimlilik konusunda cok zayif sonuc vermesidir 2 Hipotezler Pearson un ki kare test icin hipotezler soyle ifade edilir H0 lt sub sifir hipotez iki kategorili olan iki isimsel olcekle olculebilen rassal degisken birbirinden istatistiksel olarak bagimsizdir H1 alternatif hipotez iki kategorili olan isimsel olcekle olculen iki rassal degisken birbirinden istatistiksel olarak bagimsiz degildir Bu hipotezlerden acikca gorulmektedir ki sinanma icin kullanilan hipotez anakutle parametreler degerleri hakkinda degildir ve bir istatistiksel nitelik hakkindadir Boylece Pearson ki kare testi bir parametrik olmayan istatistik ornegidir Bunun yaninda dikkat edilmelidir ki alternatif hipotezin bir negatif cumle olarak ifade edilmektedir yani istatistiksel olarak bagimsiz degildir ifadesi Bu ifade pozitif vir cumle yani alternatif hipotezde iki rassal degisken istatistiksel olarak bagimlidir dememektedir Yapilan cikarimsal test analizi sonuncu sifir hipotez reddedilirse iki degiskeninin ne kadar birbirine bagimli oldugu bulunmaz bagimlilik derecesi cok kucuk olmasi mumkundur 3 Veri toplanmasi her hucresi icin gozlemlenen degerler bulunan ve marjinal toplamlar Pearson ki kare testi iki degisirli istatistiksel analize ornektir yani her bir vaka icin iki degisir hakkinda veri elde edilir Degisir icin sadece X ve Y olan iki isimsel olcekli degisken hakkinda cevap olabilir Ornegin bir ankete verilen tek kisi cevabi tek vaka dir ve arastirmada bu ankete bulunan iki soruya yani 2 degisire arastirmaci ilgisi cekilmektedir Her iki degisir de isimsel olcekli kategorik degerler alabilir Iki degisir kategorili gozlem ozetlenmesi bir kontenjans tablosu halinde olur ve Pearson ki kare testi icin pratikte kullanilan veriler bu karsilikli olarak siniflandirilmis iki degisirli kontenjans tablosu halindedir Kontenjans tablosu verileri su tip tabloda ozetler Y displaystyle Y degisiri Satir Toplami SX displaystyle X degisiri 1 2 k c nj 1 O11 O12 O1k O1r O1 2 O21 O22 O2k O2c n2 j Ojk nj r Or1 Or2 Ork Orc nc Sutun toplami S n 1 n 2 n k n c n Bu tabloda bulunan rxc adet O lt sub gt jk lt sub gt displaystyle O lt sub gt jk lt sub gt ifadesi gozlem degerleri dir ve tam sayilidirlar Her bir j satiri icin l 1 r satir toplami n j displaystyle n cdot j Her bir k sutunu icin k 1 c sutun toplami n k displaystyle n cdot k olarak bulunur ve bunlar a marjinal toplamlar adi da verilir Satir toplamlari hepsinin toplami ve sutun toplamlari hepsinin toplami toplam gozlem sayisina yani orneklem buyuklugu olan n degerine esittir 4 Teorik beklenen degerler Her bir hucre ucun bur beklenen deger yani Ejk l 1 r ve k 1 c bulunur Bu beklenen deger olasilik teoeiasinde bulunan iki bagimsiz rassal degisken olan A ve B icin carpim savi na dayanir Bu bagimsiz iki rassal degisken icin carpim savi soyle ifade edilir P A B P A P B displaystyle P A cap B P A cdot P B Bu savi kullanarak ve olasiligin asimtotik olarak relatif cokluluk a esit oldugu kabul edilip eger X ve Y degisirleri sifir hipoteze uygun olarak bagimsizlarsa her bir jk hucresi icin olasilik soyle ifade edilebilir pjk pj p k displaystyle p jk approx p j cdot cdot p cdot k Bu olasilik ifadesinin her iki tarafini da n displaystyle n ile carpilirsa her bir hucre icin beklenen deger soyle bulunur Ejk nj n kn displaystyle E jk approx frac n j cdot cdot n cdot k n 5 Hesaplanan ki kare degeri Serbestlik derecesi Hesaplanan ki kare degeri x2 j 1m k 1r Ojk Ejk 2Ejk displaystyle chi 2 sum j 1 m sum k 1 r frac O jk E jk 2 E jk Serbestlik derecesi r 1 c 1 displaystyle r 1 c 1 6 Anlamlilik seviyesi ve bu seviye icin teorik test istatistik ki kare degeri Anlamlilik seviyesi ve p degeri a displaystyle alpha wird H0 displaystyle H 0 abgelehnt wenn x2 gt x2 1 a r 1 c 1 displaystyle chi 2 gt chi 2 1 alpha r 1 c 1 dem 1 a displaystyle 1 alpha Quantil der x2 displaystyle chi 2 Verteilung mit m 1 r 1 displaystyle m 1 r 1 7 Test sonucu ve arastirma konusuUygunluk iyiligi testi Tekduze ayrik dagilim a uygunluk binom dagilim a uygunluk a uygunluk ve eger normal degerler siniflandirilip sinif ortalamasi kategori degeri gibi kullanilirsa normal dagilim a uygunluk testleri olabilirler Ayrik tekduze dagilimina uygunluk testi Bu tip problemde N displaystyle N n tane sayisal olarak belirtilmis kategorisi bulunan isimsel olcekli bir degisken bulunur Elde edilen N sayida orneklem de bu kategorilerin frekanslari coklugudur yani Veriler nx1 tipli yani n satirli ve 1 sutunlu bir ozel kontenjans tablosu halindedir ve bu tabloda n tane hucre bulunup her hucrede o hucrenin kategorisinde olan tam sayi ile ifade edilen cokluluk frekans Oi displaystyle O i i 1 n vardir Her bir hucre coklugu o kategoriye isabet eden gozlemlenen deger olarak alinir Sifir hipotez bu veri dagiliminin teorik olarak ina uyacagidir ve bu dagilima uymayacagidir Bu cok basit sifir hipotezleri ve teorik olarak her bir hucrenin birbirine esit sayida beklenen deger alacagini onerir Tekrar dikkat edilmelidir ki ki kare dagilim iyiligi testi de diger Pearson ki kare testi gibi eger sifir hipotez reddelerse zayif sonuc verir yani eldeki veriler ayrik tekduze dagilim a uymaz ama hangi dagilim uydugu bu test ile aciga cikmaz Teorik ayrik tekduze dagilimi na gore rassal degiskende her bir veri kategorisi ayni olasilik gosterir Bu nedenle N tane veri icin her bir i kategorisi icin ayni deger tasiyan beklenen deger E yani E Nn displaystyle E frac N n olarak hesaplanir Hesaplanan ki kare degeri her hucre icin gozlemlenen deger eksi beklenen deger farkinin karesinin beklenen deger e bolunmesinin tum hucreler icin toplanmasidir Yani X2 i 1n Oi E 2E displaystyle mathrm X 2 sum i 1 n frac O i E 2 E Test istatistiginin hesaplanmasi Uygunluk iyiligi sinamasi icin test istatistigi su formule gore hesaplanmis X2 i 1n Oi Ei 2Ei displaystyle mathrm X 2 sum i 1 n frac O i E i 2 E i Bu formulde X2 displaystyle mathrm X 2 Pearson un kumulatif test istatistigi olup bu hesaplanmis x2 displaystyle chi 2 degeri asimtotik olarak bir na yakinlasmaktadir Oi displaystyle O i gozlenen cokluluk degeri Ei displaystyle E i sifir hipotez onerisinin gercek oldugu kabul edilerek bir teorik beklenmekte olan cokluluk degerdir n displaystyle n tabloda bulunan hucre sayisi yatay x ekseni hesaplanmis x2 displaystyle chi 2 degerlerini dikey Y ekseni ise P degerleridir Ayrica bakinizKi kare dagilimi Ki kare testiKaynakca Karl Pearson 1900 On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling Philosophical Magazine Series 5 50 302 ss 157 175 doi 10 1080 14786440009463897 Dis baglantilarEric W Weisstein Chi Squared Test MathWorld Greenwood P E Nikulin M S 1996 A guide to chi squared testing New York J Wiley ISBN 0 471 55779 X
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans