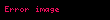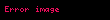Azərbaycanca
Deutsch
日本語
Lietuvos
සිංහල
Türkçe
Українська
United State
Poisson-Boltzmann denklemi elektrolitler içindeki moleküller arasındaki elektrostatik etkileşimleri açıklayan diferansiyel denklemlere denir. Bu denklem aynı zamanda Gouy-Chapman 'nın matematiksel temelidir; ilk olarak tarafından tasarlanmış daha sonra Chapman tarafından 1913te tamamlanmıştır. Bu denklem moleküler dinamikte ve önemlidir, zira bu denklem, çözücünün yapılar üzerindeki etkilerine ve farklı iyonik güçlere sahip çözeltilerdeki proteinlerin, DNAnın, RNAnın ve diğer moleküllerin etkileşimlerine yaklaşım yapılmasında ve de modellemede kullanılmaktadır. Genellikle Poisson-Boltmann denklemini kompleks sistelerde çözmek zordur, fakat birçok bilgisayar programı onu numerik olarak çözmek için geliştirilmiştir.
Bu denklem cgsde şu şekilde yazılır :
veya mksde :
![{\displaystyle {\vec {\nabla }}\cdot \left[\epsilon ({\vec {r}}){\vec {\nabla }}\Psi ({\vec {r}})\right]=-\rho ^{f}({\vec {r}})-\sum _{i}c_{i}^{\infty }z_{i}q\lambda ({\vec {r}})\cdot \exp \left[{\frac {-z_{i}q\Psi ({\vec {r}})}{k_{B}T}}\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NU5ERTRaR1JrT0RnM01UYzROR1ZqTXpZd1pUVXdNV000T1dZMU9UYzROekU1TkdOaU56RTUuc3Zn.svg)
burada diverjansa, konuma bağlı dielektriğe, elektrostatik potansiyelin gradyanına, çözünenin yük yoğunluğuna, çözeltiden sonsuz uzaklıktaki iyon i yoğunluğuna, iyonun yüküne, q protonun yüküne, Boltzmann sabitine T sıcaklığa ve çözeltide r konumunun iyonlara konuma bağlı erişilebilirliğini belirleyen bir faktöre tekamül etmektedir. Eğerki potansiyel kT'ye kıyasla büyük değilse, denklemin daha verimli çözülebilmesi için , ki bu da ortaya çıkarır.
Ayrıca bakınız
- : bugün bedava yazılım olarak dağıtılan protein için Poisson-Boltzmann çözücüsü
Kaynakça
Dış bağlantılar
- Adaptive Poisson–Boltzmann Solver18 Mart 2014 tarihinde Wayback Machine sitesinde .
- Zap21 Ağustos 2008 tarihinde Wayback Machine sitesinde . - A Poisson–Boltzmann electrostatics solver.
- MIBPB 24 Ocak 2011 tarihinde Wayback Machine sitesinde . Matched Interface & Boundary based Poisson–Boltzmann solver
- CHARMM-GUI: PBEQ Solver[]
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Poisson Boltzmann denklemi elektrolitler icindeki molekuller arasindaki elektrostatik etkilesimleri aciklayan diferansiyel denklemlere denir Bu denklem ayni zamanda Gouy Chapman nin matematiksel temelidir ilk olarak tarafindan tasarlanmis daha sonra Chapman tarafindan 1913te tamamlanmistir Bu denklem molekuler dinamikte ve onemlidir zira bu denklem cozucunun yapilar uzerindeki etkilerine ve farkli iyonik guclere sahip cozeltilerdeki proteinlerin DNAnin RNAnin ve diger molekullerin etkilesimlerine yaklasim yapilmasinda ve de modellemede kullanilmaktadir Genellikle Poisson Boltmann denklemini kompleks sistelerde cozmek zordur fakat bircok bilgisayar programi onu numerik olarak cozmek icin gelistirilmistir Bu denklem cgsde su sekilde yazilir ϵ r PS r 4prf r 4p ici ziql r exp ziqPS r kBT displaystyle vec nabla cdot left epsilon vec r vec nabla Psi vec r right 4 pi rho f vec r 4 pi sum i c i infty z i q lambda vec r cdot exp left frac z i q Psi vec r k B T right veya mksde ϵ r PS r rf r ici ziql r exp ziqPS r kBT displaystyle vec nabla cdot left epsilon vec r vec nabla Psi vec r right rho f vec r sum i c i infty z i q lambda vec r cdot exp left frac z i q Psi vec r k B T right burada displaystyle vec nabla cdot diverjansa ϵ r displaystyle epsilon vec r konuma bagli dielektrige PS r displaystyle vec nabla Psi vec r elektrostatik potansiyelin gradyanina rf r displaystyle rho f vec r cozunenin yuk yogunluguna ci displaystyle c i infty cozeltiden sonsuz uzakliktaki iyon i yogunluguna zi displaystyle z i iyonun yukune q protonun yukune kB displaystyle k B Boltzmann sabitine T sicakliga ve l r displaystyle lambda vec r cozeltide r konumunun iyonlara konuma bagli erisilebilirligini belirleyen bir faktore tekamul etmektedir Egerki potansiyel kT ye kiyasla buyuk degilse denklemin daha verimli cozulebilmesi icin ki bu da ortaya cikarir Ayrica bakiniz bugun bedava yazilim olarak dagitilan protein icin Poisson Boltzmann cozucusuKaynakca Fogolari F Brigo A Molinari H 2002 The Poisson Boltzmann equation for biomolecular electrostatics a tool for structural biology J Mol Recognit 15 6 377 392 See this paper for derivation G L Gouy j de phys 9 457 1910 D L Chapman Philos Mag 25 475 1913 Dis baglantilarVikiversite dePoisson Boltzmann denklemi ile ilgili kaynaklar bulunur Adaptive Poisson Boltzmann Solver18 Mart 2014 tarihinde Wayback Machine sitesinde Zap21 Agustos 2008 tarihinde Wayback Machine sitesinde A Poisson Boltzmann electrostatics solver MIBPB24 Ocak 2011 tarihinde Wayback Machine sitesinde Matched Interface amp Boundary based Poisson Boltzmann solver CHARMM GUI PBEQ Solver olu kirik baglanti