Rassal değişken kavramının geliştirilmesi ile, sezgi yoluyla anlaşılan şans kavramı, soyutlaştırarak teorik matematik analiz alanına sokulmuş ve bu geliştirilen matematik kavram ile olasılık kuramı ve matematiksel istatistiğin temeli kurulmuştur.
Son birkaç yüzyılda olasılıkla ilgili matematiksel fikirler geliştirilirken rassal değişkenlerlerle ilişkili teori ve kullanım matematik kuramı biçimlerine konulmuştur. Rassal değişkenleri modern matematik görüşle tam olarak anlamak için, daha yakın zamanlarda matematikçiler tarafından geliştirilmiş olan hakkında geniş bilginin kazanılması gerekmektedir. Rassal değişken kavramı, bu kuram içinde tüm özellikleri ile arka planda kalmakla beraber, kuramın içeriğinde önemli bir yeri bulunmaktadır. Bununla beraber, rassal değişkenler kavramının matematiksel teoride değişik ileri seviyelerde fazla teori gerektirmeyen çok daha az ileri matematiksel bilgisi ile de anlaşılması mümkündür. Böylece rassal değişkenler hakkında temel bilgileri anlamak için sadece küme kuramı ve bilinmesi yeterli olmaktadır.
Geniş bir tanımlama ile, bir rassal değişken, değerleri rassal olan ve bu değerler için bir olasılık dağılımı saptamak imkânı olan bir sayıdır. Daha matematiksel biçimde, bir rassal değişken bir örneklem uzayından değişkenin mümkün değerlerinden oluşan değişimi gösterir. Rassal değiskenlerin bu formel tanımlanması reel değerli sonuçlar veren deneyleri çok sıkı bir surette matematiksel ölçüm kuramı çerçevesi içine sokmakta ve reel değerli rassal değişkenler için dağılım fonksiyonu kurulmasına imkân sağlamaktadır.
Sezgisel tanımlama
Genellikle bir rassal değişken sayı şeklinde değerler alır. Ama bu her zaman doğru değildir; çünkü vektör, karmaşık sayılar, sıralamalar veya fonksiyonlardan oluşan rassal değişkenler bulunmaktadır. Eğer değişkenler reel-değerli iseler o zaman bir rassal değişken her ele alınıp incelendiği zaman değer değiştirebilen bir bilinmez sayı olarak düşünülebilir. Böylece bir rassal değişken bir rastgele sürecinin örnek uzayını bir sayı setine eşlemesini yapan bir fonksiyon olarak görülebilir. Bunu daha göze çarpar bir şekilde şu örneğinlerle gösterebiliriz:
Örnekler
Hileli olmayan bir metal parayı havaya atma ve hangi yüzü geleceğini ele alma deneyini önce ele alalım. Tek bir deney için mümkün sonuç olaylar ya "yazı" ya da "tura" olur. Birkaç defa para atılması ve bunlardan kaç tane yazı geleceği şu rassal değişken ile ifade edilebilir:
ve eğer metal para için bu iki sonuç eşit olabilirlikli ise o zaman bu rassal değişken için bir olasılık kütle fonksiyonu bulunur ve şöyle ifade edilir:
Bazen daha kolaylık sağlamak için bu haldeki değerler olarak ("yazı" veya "tura" kategorileri yerine) sayılar şeklinde olan bir rassal değişken tanımlanabilir. Bunu 
ve eğer metal para için bu iki sonuç için her iki taraf eşit olabilirlikli ise o zaman olasılık kütle fonksiyonu şöyle ifade edilir:
Bir rassal ayrık rassal değişken kavramı kullanılması için diğer bir örneğin, hileli olmayan bir zar atılması ve düşen zarda üste gelen nokta sayısını görme şeklindeki deneyidir. Bu halde en basit açıklama, olası sonuçlar olan {1, 2, 3, 4, 5, 6} sayıları setinin "örnek uzayı" ve zar atınca gelen sayı X'in de rassal değişken şeklinde yapılabilir. Bu halde
Bir sürekli rassal değişken için bir örnek sonunda belli bir yöne yönelip kalan bir döner ibreli aletin ibresi ele alınabilir. Bu örneğinde rassal değişken tarafından sonuç değerler yönlerdir. Bu yönler ayrık olarak Kuzey batı, Doğu güneydoğu vb. şekilde ifade edilebilirler. Fakat genellikle örnek uzayını bir rassal değişkene eşlendirilmesi yapılırken reel sayılar kullanmak daha kullanışlı olacaktır. Bunu başarmak için döner ibresini son durma yönünü Kuzey'den olan saat yönündeki açısının derece birimi ile ifade edebiliriz. Böylece rassal değişken [O, 360] aralığında herhangi bir sayı şekilde ifade edilir ve her bir mümkün sayının açıklığı rasgelirliği "eşit olasılıklı"dır. Bu halde rassal değişken X= ibre duruş açısı olur. Herhangi bir belirli sayının olasılığı 0 olur ama bir sayısal aralık için bir pozitif olasılık sayısı verilebilir. Örneğin, [0,180] arasında bir sayının gelme olasılığı ½ olur. Bu halde olasılık kütle yoğunluk fonksiyonu demeyiz ama X için olasılık yoğunluğu 1/360 olur. (0, 360) alt-seti icin olasılık bu setin ölçüsünü 1/360 ile çarpma ile elde edilir. Genel olarak, bir belirlenmemiş sürekli rassal değişken seti için olasılık yoğunluğun verilmiş set üzerinde entegrasyonunu bulmak suretiyle elde edilir.
Karışık ayrık ve sürekli rassal değişken için örneğin bir matal parayı atmak ile eğer para "yazı" gelmişse bir döner ibreli aletin ibresini döndürmek şeklinde verilebilir. Bu deneyin sonucunun matematiksel ifadesi şöyle olur: Eğer para atış "tura" gelirse X= -1; aksi halde X döner ibreli aletin ibresinin durduğunda gösterdiği yönün Kuzeye göre saat yönündeki açı değeridir. Bu ikili deney için rassal değişken değerinin -1 olma olasılığı ½ olur; diğer aralıklar için rassal değişken değerleri bir önceki deneyin sonuçlarının yarısına eşittir.
Reel değerli rassal değişkenler
Bu halde, 
olur.
Rassal değişkenlerin dağılım fonksiyonları
Bir yığmalı dağılım fonksiyonunu belli bir rassal değişkeni ile birlikte olduğunu düşünmek bir değişkene bir değer tahsis etmenin bir genelleştirilmesidir. Eğer yığmalı dağılım fonksiyonu sağdan sürekli bir ise, o halde rassal değişken bu sıçrama için 1 olasılık değerini alır. Genel olarak, yığmalı dağılım fonksiyonu değişkenin belirli değerinde ne olasılık göstereceğini tanımlar.
Eğer
olasılık uzayında tanımlanmış bir rassal değişken olan
bilinmekte ise, şu şekilde soru sorulabilir:
- "
in değerinin 2 den büyük olması ne kadar olabilirliktedir?".
Bunu aynı anlamda
- "
olayının olasılığı nedir?"
olarak sorabiliriz veya matematiksel ifade ile kısaca 
Bir reel değerli rassal değişken olan Xin çıktılarının bütün değerlerinin olasılıklarının hepsinin kaydı yapılırsa X için olasılık dağılımı ortaya çıkar. Olasılık dağılımı Xi tanımlamak için kullanılan belirli bir olasılık uzayını unutur ve sadece X çeşitli değerlerinin olasılığını kaydeder. Bu türlü olasılık dağılımı her zaman şu yığmalı dağılım fonksiyonu tarafından ele geçirilebilir:
ve bazen de ele geçirme bir olasılık yoğunluk fonksiyonu kullanılarak gerçekleştirilebilir. rassal değişken olan Xi Ω üzerindeki P ölçüsünü R üzerinde bir F ölçüsüne "ileri itmek" için kullanırız.
Teorinin altında bulunan Ω olasılık uzayı rassal değişkenlerin varoluşlarını garanti etmek için, bazen de onları inşa etmek için bir teknik gereçtir. Pratikte çok defa Ω uzayı tümüyle bir tarafa bırakılır. Doğrudan doğruya R üzerine reel doğrunun tümüne 1 ölçü değeri tahsis eden bir yeni ölçü koyulur. Yani rassal değişkenler yerine olasılık dağılımları doğrudan doğruya kullanılır.
Momentler
Bir rassal değişkenin olasılık dağılımı, çok kere pratikte anlanması ve uygulanması kolay olan küçük sayıda parametreler ile nitelendirilir. Örneğin, sadece "ortalama değer" olan λ değerini bilmek Poisson dağılımını bilmek için yeterlidir. Ortalama kavramı matematik teoride bir rassal değişkenin beklenen değeri olarak, yani E[X] olarak ifade edilir. Genellikle E[f(X)] ifadesi f(E[X]) ifadesine eşit değildir. "Ortalama değer" bilinince, bu ortalama değerin X tipik değerlerinden ne kadar fazla uzaklıkta olduğu sorusu hemen akla gelir ve bu soruya yanıt bu rassal değişkenin standart sapması ve varyansı ile bulunur.
Matematik kuramı içinde bu (genelleştirilmiş) olarak bilinmektedir: Bilinmekte olan bir sınıf rassal değişkenler olan X için, E[fi(X)] ifadesindeki beklenen değerler ile rassal değişken Xin dağılımını tam olarak nitelendiren bir {fi} fonksiyonlar koleksiyonu bulunması istenmektedir.
Rassal değişkenlerin fonksiyonları
Eğer X rassal değişkeni Ω üzerinde bulunursa ve f R → R ise, bu halde de Y = f(X) de Ω, üzerinde bir rassal değişken olacaktır. Buna neden ölçüculebilir bir fonksiyonun kompozisyonu da ölçüulebilir olmalıdır. Bizi bir olasılık uzayi olan (Ω, P) den (R, dFX)ye gitmemize izin veren yordam Y için dağılımı bulmak için de kullanılabilir. Y için yığmalı dağılım fonksiyonu
olur.
Örnek 1
X reel değerli bir olsun ve Y = X2 olsun. O halde,
Eğer y<0, o halde
- P(X2 ≤ y) = 0,
ve bu nedenle
Eğer y ≥ 0 ise, o zaman
olur ve bundan dolayı
Örnek 2
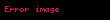
Burada 

Bu son ifade 
Rassal değişkenlerin birbirine eşitliliği
Rassal değişkenlerin birbirlerine eşitliliği kavramı birbirlerinden değişik anlamları olan çeşitli şekillerde açıklanabilir. Bu değişik şekiller şöyle sıralanabilir: iki rassal değişkenin eşitliliği; nerede ise kesinlikle eşitliği; ortalama olarak eşitliliği; dağılım içinde eşitliliği. Bu sıralama değişik eşitlilik kavramının tarifinin artan teorik sıkılığına göre (en çok bağlayıcı tanımdan en zayıf tanıma doğru) yapılmıştır. Bu değişik eşitlilik kavramların ayrıntılı tanımları aşağıda verilmektedir.
Dağılım içinde eşitlilik
İki rassal değişken X ve Y eğer aynı dağılım fonksiyonuna sahip iseler; yani
ise, dağılım içinde eşitlilik gösterirler
Birbirine eşit moment üreten fonksiyonu olan iki rassal değişken de aynı dağılımı gösterir. Örneğin, bu çeşit eşitlilik bazı fonksiyonların eşit olup olmadıklarını kontrol etmek için kullanılır bir yöntem olabilir.
Dağılım içinde eşitlilik göstermeleri için rassal değişkenlerin aynı olasılık uzayında tanımlanmalarına gerek yoktur. Dağılım içinde eşitlilik kavramı, olasılık dağılımları arasında bulunan uzaklık kavramı ile şöyle ifade edilen yakın bir ilişkisi bulunmaktadır:
Bu tanımlama Kolmogorov-Smirnov sınaması için temel teoriyi sağlar.
Ortalamada eşitlilik
İki rassal değişken X ve Y için, eğer |X - Y| nin p-inci momenti sıfır ise; yani
ise p-inci ortalama için eşitlilik kavramı tanımı ortaya çıkar.
p-inci ortalama eşitlilik kavramı aynı zamanda her r<p için r-inci ortalama için eşitlilik anlamını içerir.
Daha önceki eşitlik tanımına benzer olarak, bu kavrama göre de iki rassal değişken arasında bir uzaklık ilişkisi şu ifade ile açıklanabilir:
Nerede ise kesinlikle eşitlilik
İki rassal değişken X ve Y birbirine nerede ise kesinlikle eşitliliği sadece ve sadece iki değişken için birbirinden farklı olma olasılığı sıfır olursa, yani
olursa ortaya çıkar:
Olasılık kuramının pratik kullanılması için bu tanımlama ve bu kavrama gore iki olasılık değişkeninin birbirine eşitliliği hiç olmazsa diğer eşitlilik kavramları kadar kesindir.
Bu tanımlama şu uzaklık kavramı ile ilişkilidir:
Burada 'sup' içindeki kavramını ifade eder.
Eşitlilik
Sonuncu tanıma göre ise, eğer olasılık uzaylarında fonksiyonlar olarak birbirine eşitlerse, yani
olursa, iki rassal değişken olan X ve Y birbirine eşittirler.
Yakınsalama
Matematik istatistik analizinin büyük bir kısmı bazı rassal değişkenler serilerinin yakınsalama sonuçlarının geliştirilmesinden oluşmuştur. Örneğin, büyük sayılar yasası ve merkezsel limit teoremi maddelerine bakın.
Bir rassal değişken serisi olan Xnnin limitte bir rassal değişken olan X'e yakınsalaması değişik tanımlamalara göre değişmektedir; bunun için maddesine bakın.
Ayrıca bakınız
Kaynakça
- , Random Measures, 4th edition. Academic Press, New York, London; Akademie-Verlag, Berlin (1986). MR0854102
- Papoulis, Athanasios 1965 Probability, Random Variables, and Stochastic Processes. McGraw-Hill Kogakusha, Tokyo, 9th edition, .
Bu makale PlanetMath'deki Random variable maddesinden lisansıyla faydalanmaktadır.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Rassal degisken kavraminin gelistirilmesi ile sezgi yoluyla anlasilan sans kavrami soyutlastirarak teorik matematik analiz alanina sokulmus ve bu gelistirilen matematik kavram ile olasilik kurami ve matematiksel istatistigin temeli kurulmustur Son birkac yuzyilda olasilikla ilgili matematiksel fikirler gelistirilirken rassal degiskenlerlerle iliskili teori ve kullanim matematik kurami bicimlerine konulmustur Rassal degiskenleri modern matematik gorusle tam olarak anlamak icin daha yakin zamanlarda matematikciler tarafindan gelistirilmis olan hakkinda genis bilginin kazanilmasi gerekmektedir Rassal degisken kavrami bu kuram icinde tum ozellikleri ile arka planda kalmakla beraber kuramin iceriginde onemli bir yeri bulunmaktadir Bununla beraber rassal degiskenler kavraminin matematiksel teoride degisik ileri seviyelerde fazla teori gerektirmeyen cok daha az ileri matematiksel bilgisi ile de anlasilmasi mumkundur Boylece rassal degiskenler hakkinda temel bilgileri anlamak icin sadece kume kurami ve bilinmesi yeterli olmaktadir Genis bir tanimlama ile bir rassal degisken degerleri rassal olan ve bu degerler icin bir olasilik dagilimi saptamak imkani olan bir sayidir Daha matematiksel bicimde bir rassal degisken bir orneklem uzayindan degiskenin mumkun degerlerinden olusan degisimi gosterir Rassal degiskenlerin bu formel tanimlanmasi reel degerli sonuclar veren deneyleri cok siki bir surette matematiksel olcum kurami cercevesi icine sokmakta ve reel degerli rassal degiskenler icin dagilim fonksiyonu kurulmasina imkan saglamaktadir Sezgisel tanimlamaGenellikle bir rassal degisken sayi seklinde degerler alir Ama bu her zaman dogru degildir cunku vektor karmasik sayilar siralamalar veya fonksiyonlardan olusan rassal degiskenler bulunmaktadir Eger degiskenler reel degerli iseler o zaman bir rassal degisken her ele alinip incelendigi zaman deger degistirebilen bir bilinmez sayi olarak dusunulebilir Boylece bir rassal degisken bir rastgele surecinin ornek uzayini bir sayi setine eslemesini yapan bir fonksiyon olarak gorulebilir Bunu daha goze carpar bir sekilde su orneginlerle gosterebiliriz Ornekler Hileli olmayan bir metal parayi havaya atma ve hangi yuzu gelecegini ele alma deneyini once ele alalim Tek bir deney icin mumkun sonuc olaylar ya yazi ya da tura olur Birkac defa para atilmasi ve bunlardan kac tane yazi gelecegi su rassal degisken ile ifade edilebilir X yazi tura displaystyle X begin cases yazi tura end cases ve eger metal para icin bu iki sonuc esit olabilirlikli ise o zaman bu rassal degisken icin bir olasilik kutle fonksiyonu bulunur ve soyle ifade edilir rX x 12 if x yazi 12 if x tura displaystyle rho X x begin cases frac 1 2 amp text if x yazi frac 1 2 amp text if x tura end cases Bazen daha kolaylik saglamak icin bu haldeki degerler olarak yazi veya tura kategorileri yerine sayilar seklinde olan bir rassal degisken tanimlanabilir Bunu Y displaystyle Y reel rassal degiskenini kullanarak ve bunu su sekilde tanimlayarak yapabiliriz Y 1 eger yazi ise 0 eger tura ise displaystyle Y begin cases 1 amp text eger yazi ise 0 amp text eger tura ise end cases ve eger metal para icin bu iki sonuc icin her iki taraf esit olabilirlikli ise o zaman olasilik kutle fonksiyonu soyle ifade edilir rY y 12 eger y 0 12 if y 1 0 aksi halde displaystyle rho Y y begin cases frac 1 2 amp text eger y 0 frac 1 2 amp text if y 1 0 amp text aksi halde end cases Bir rassal ayrik rassal degisken kavrami kullanilmasi icin diger bir ornegin hileli olmayan bir zar atilmasi ve dusen zarda uste gelen nokta sayisini gorme seklindeki deneyidir Bu halde en basit aciklama olasi sonuclar olan 1 2 3 4 5 6 sayilari setinin ornek uzayi ve zar atinca gelen sayi X in de rassal degisken seklinde yapilabilir Bu halde X 1 eger 1 gelirse 2 eger 2 gelirse 3 eger 3 gelirse 4 eger 4 gelirse 5 eger 5 gelirse 6 eger 6 gelirse displaystyle X begin cases 1 amp text eger 1 gelirse 2 amp text eger 2 gelirse 3 amp text eger 3 gelirse 4 amp text eger 4 gelirse 5 amp text eger 5 gelirse 6 amp text eger 6 gelirse end cases rX x 16 eger x 1 2 3 4 5 6 0 aksi halde displaystyle rho X x begin cases frac 1 6 amp text eger x 1 2 3 4 5 6 0 amp text aksi halde end cases Bir surekli rassal degisken icin bir ornek sonunda belli bir yone yonelip kalan bir doner ibreli aletin ibresi ele alinabilir Bu orneginde rassal degisken tarafindan sonuc degerler yonlerdir Bu yonler ayrik olarak Kuzey bati Dogu guneydogu vb sekilde ifade edilebilirler Fakat genellikle ornek uzayini bir rassal degiskene eslendirilmesi yapilirken reel sayilar kullanmak daha kullanisli olacaktir Bunu basarmak icin doner ibresini son durma yonunu Kuzey den olan saat yonundeki acisinin derece birimi ile ifade edebiliriz Boylece rassal degisken O 360 araliginda herhangi bir sayi sekilde ifade edilir ve her bir mumkun sayinin acikligi rasgelirligi esit olasilikli dir Bu halde rassal degisken X ibre durus acisi olur Herhangi bir belirli sayinin olasiligi 0 olur ama bir sayisal aralik icin bir pozitif olasilik sayisi verilebilir Ornegin 0 180 arasinda bir sayinin gelme olasiligi olur Bu halde olasilik kutle yogunluk fonksiyonu demeyiz ama X icin olasilik yogunlugu 1 360 olur 0 360 alt seti icin olasilik bu setin olcusunu 1 360 ile carpma ile elde edilir Genel olarak bir belirlenmemis surekli rassal degisken seti icin olasilik yogunlugun verilmis set uzerinde entegrasyonunu bulmak suretiyle elde edilir Karisik ayrik ve surekli rassal degisken icin ornegin bir matal parayi atmak ile eger para yazi gelmisse bir doner ibreli aletin ibresini dondurmek seklinde verilebilir Bu deneyin sonucunun matematiksel ifadesi soyle olur Eger para atis tura gelirse X 1 aksi halde X doner ibreli aletin ibresinin durdugunda gosterdigi yonun Kuzeye gore saat yonundeki aci degeridir Bu ikili deney icin rassal degisken degerinin 1 olma olasiligi olur diger araliklar icin rassal degisken degerleri bir onceki deneyin sonuclarinin yarisina esittir Reel degerli rassal degiskenlerBu halde W F P displaystyle scriptstyle Omega mathcal F P bir olasilik uzayi olsun O zaman bir rassal degisken olan X formel bir taninimla X W PS displaystyle X Omega to Psi olur Rassal degiskenlerin dagilim fonksiyonlari Bir yigmali dagilim fonksiyonunu belli bir rassal degiskeni ile birlikte oldugunu dusunmek bir degiskene bir deger tahsis etmenin bir genellestirilmesidir Eger yigmali dagilim fonksiyonu sagdan surekli bir ise o halde rassal degisken bu sicrama icin 1 olasilik degerini alir Genel olarak yigmali dagilim fonksiyonu degiskenin belirli degerinde ne olasilik gosterecegini tanimlar Eger W A P displaystyle Omega A P olasilik uzayinda tanimlanmis bir rassal degisken olan X W R displaystyle X Omega to mathbb R bilinmekte ise su sekilde soru sorulabilir X displaystyle X in degerinin 2 den buyuk olmasi ne kadar olabilirliktedir Bunu ayni anlamda s W X s gt 2 displaystyle s in Omega X s gt 2 olayinin olasiligi nedir olarak sorabiliriz veya matematiksel ifade ile kisaca P X gt 2 displaystyle P X gt 2 olarak yazabiliriz Bir reel degerli rassal degisken olan Xin ciktilarinin butun degerlerinin olasiliklarinin hepsinin kaydi yapilirsa X icin olasilik dagilimi ortaya cikar Olasilik dagilimi Xi tanimlamak icin kullanilan belirli bir olasilik uzayini unutur ve sadece X cesitli degerlerinin olasiligini kaydeder Bu turlu olasilik dagilimi her zaman su yigmali dagilim fonksiyonu tarafindan ele gecirilebilir FX x P X x displaystyle F X x operatorname P X leq x ve bazen de ele gecirme bir olasilik yogunluk fonksiyonu kullanilarak gerceklestirilebilir rassal degisken olan Xi W uzerindeki P olcusunu R uzerinde bir F olcusune ileri itmek icin kullaniriz Teorinin altinda bulunan W olasilik uzayi rassal degiskenlerin varoluslarini garanti etmek icin bazen de onlari insa etmek icin bir teknik gerectir Pratikte cok defa W uzayi tumuyle bir tarafa birakilir Dogrudan dogruya R uzerine reel dogrunun tumune 1 olcu degeri tahsis eden bir yeni olcu koyulur Yani rassal degiskenler yerine olasilik dagilimlari dogrudan dogruya kullanilir Momentler Bir rassal degiskenin olasilik dagilimi cok kere pratikte anlanmasi ve uygulanmasi kolay olan kucuk sayida parametreler ile nitelendirilir Ornegin sadece ortalama deger olan l degerini bilmek Poisson dagilimini bilmek icin yeterlidir Ortalama kavrami matematik teoride bir rassal degiskenin beklenen degeri olarak yani E X olarak ifade edilir Genellikle E f X ifadesi f E X ifadesine esit degildir Ortalama deger bilinince bu ortalama degerin X tipik degerlerinden ne kadar fazla uzaklikta oldugu sorusu hemen akla gelir ve bu soruya yanit bu rassal degiskenin standart sapmasi ve varyansi ile bulunur Matematik kurami icinde bu genellestirilmis olarak bilinmektedir Bilinmekte olan bir sinif rassal degiskenler olan X icin E fi X ifadesindeki beklenen degerler ile rassal degisken Xin dagilimini tam olarak nitelendiren bir fi fonksiyonlar koleksiyonu bulunmasi istenmektedir Rassal degiskenlerin fonksiyonlariEger X rassal degiskeni W uzerinde bulunursa ve f R R ise bu halde de Y f X de W uzerinde bir rassal degisken olacaktir Buna neden olcuculebilir bir fonksiyonun kompozisyonu da olcuulebilir olmalidir Bizi bir olasilik uzayi olan W P den R dFX ye gitmemize izin veren yordam Y icin dagilimi bulmak icin de kullanilabilir Y icin yigmali dagilim fonksiyonu FY y P f X y displaystyle F Y y operatorname P f X leq y olur Ornek 1 X reel degerli bir olsun ve Y X2 olsun O halde FY y P X2 y displaystyle F Y y operatorname P X 2 leq y Eger y lt 0 o halde P X2 y 0 ve bu nedenle FY y 0ify lt 0 displaystyle F Y y 0 qquad hbox if quad y lt 0 Eger y 0 ise o zaman P X2 y P X y P y X y displaystyle operatorname P X 2 leq y operatorname P X leq sqrt y operatorname P sqrt y leq X leq sqrt y olur ve bundan dolayi FY y FX y FX y egery 0 displaystyle F Y y F X sqrt y F X sqrt y qquad hbox eger quad y geq 0 Ornek 2 X displaystyle scriptstyle X bir rassal degisken olsun ve yigmali dagilimi soyle ifade edilsin FX x P X x 1 1 e x 8 displaystyle F X x P X leq x frac 1 1 e x theta Burada 8 gt 0 displaystyle scriptstyle theta gt 0 sabit bir parametredir Simdi su rassal degiskene yani Y log 1 e X displaystyle scriptstyle Y mathrm log 1 e X bakilsin O zaman FY y P Y y P log 1 e X y P X gt log ey 1 displaystyle F Y y P Y leq y P mathrm log 1 e X leq y P X gt mathrm log e y 1 Bu son ifade X displaystyle X in yigmali dagilimi terimleri ile soyle hesaplanabilir FY y 1 FX log ey 1 displaystyle F Y y 1 F X mathrm log e y 1 1 1 1 elog ey 1 8 displaystyle 1 frac 1 1 e mathrm log e y 1 theta 1 1 1 ey 1 8 displaystyle 1 frac 1 1 e y 1 theta 1 e y8 displaystyle 1 e y theta dd dd Rassal degiskenlerin birbirine esitliligiRassal degiskenlerin birbirlerine esitliligi kavrami birbirlerinden degisik anlamlari olan cesitli sekillerde aciklanabilir Bu degisik sekiller soyle siralanabilir iki rassal degiskenin esitliligi nerede ise kesinlikle esitligi ortalama olarak esitliligi dagilim icinde esitliligi Bu siralama degisik esitlilik kavraminin tarifinin artan teorik sikiligina gore en cok baglayici tanimdan en zayif tanima dogru yapilmistir Bu degisik esitlilik kavramlarin ayrintili tanimlari asagida verilmektedir Dagilim icinde esitlilik Iki rassal degisken X ve Y eger ayni dagilim fonksiyonuna sahip iseler yani P X x P Y x for allx displaystyle operatorname P X leq x operatorname P Y leq x quad hbox for all quad x ise dagilim icinde esitlilik gosterirler Birbirine esit moment ureten fonksiyonu olan iki rassal degisken de ayni dagilimi gosterir Ornegin bu cesit esitlilik bazi fonksiyonlarin esit olup olmadiklarini kontrol etmek icin kullanilir bir yontem olabilir Dagilim icinde esitlilik gostermeleri icin rassal degiskenlerin ayni olasilik uzayinda tanimlanmalarina gerek yoktur Dagilim icinde esitlilik kavrami olasilik dagilimlari arasinda bulunan uzaklik kavrami ile soyle ifade edilen yakin bir iliskisi bulunmaktadir d X Y supx P X x P Y x displaystyle d X Y sup x operatorname P X leq x operatorname P Y leq x Bu tanimlama Kolmogorov Smirnov sinamasi icin temel teoriyi saglar Ortalamada esitlilik Iki rassal degisken X ve Y icin eger X Y nin p inci momenti sifir ise yani E X Y p 0 displaystyle operatorname E X Y p 0 ise p inci ortalama icin esitlilik kavrami tanimi ortaya cikar p inci ortalama esitlilik kavrami ayni zamanda her r lt p icin r inci ortalama icin esitlilik anlamini icerir Daha onceki esitlik tanimina benzer olarak bu kavrama gore de iki rassal degisken arasinda bir uzaklik iliskisi su ifade ile aciklanabilir dp X Y E X Y p displaystyle d p X Y operatorname E X Y p Nerede ise kesinlikle esitlilik Iki rassal degisken X ve Y birbirine nerede ise kesinlikle esitliligi sadece ve sadece iki degisken icin birbirinden farkli olma olasiligi sifir olursa yani P X Y 0 displaystyle operatorname P X neq Y 0 olursa ortaya cikar Olasilik kuraminin pratik kullanilmasi icin bu tanimlama ve bu kavrama gore iki olasilik degiskeninin birbirine esitliligi hic olmazsa diger esitlilik kavramlari kadar kesindir Bu tanimlama su uzaklik kavrami ile iliskilidir d X Y supw X w Y w displaystyle d infty X Y sup omega X omega Y omega Burada sup icindeki kavramini ifade eder Esitlilik Sonuncu tanima gore ise eger olasilik uzaylarinda fonksiyonlar olarak birbirine esitlerse yani X w Y w butunw displaystyle X omega Y omega qquad hbox butun quad omega olursa iki rassal degisken olan X ve Y birbirine esittirler YakinsalamaMatematik istatistik analizinin buyuk bir kismi bazi rassal degiskenler serilerinin yakinsalama sonuclarinin gelistirilmesinden olusmustur Ornegin buyuk sayilar yasasi ve merkezsel limit teoremi maddelerine bakin Bir rassal degisken serisi olan Xnnin limitte bir rassal degisken olan X e yakinsalamasi degisik tanimlamalara gore degismektedir bunun icin maddesine bakin Ayrica bakinizBagimsiz ve ozdes dagilmis rastgele degisken Olasilik dagilimi Olay olasilik teorisi Rastsallik Stokastik surecKaynakca Random Measures 4th edition Academic Press New York London Akademie Verlag Berlin 1986 MR0854102 ISBN 0 12 394960 2 Papoulis Athanasios 1965 Probability Random Variables and Stochastic Processes McGraw Hill Kogakusha Tokyo 9th edition ISBN 0 07 119981 0 Bu makale PlanetMath deki Random variable maddesinden GFDL lisansiyla faydalanmaktadir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State