Stokastik süreç, Stokastik işlemi (veya rastgele süreç), zaman veya mekana göre değişen/evrilen olguları tanımlamak için kullanılan bir olasılık modelidir. Daha kapsamlı olarak, olasılık teorisinde, stokastik süreç, değişimi rastgele bir varyasyona bağlı olan bir değişken tarafından temsil edilen bazı sistemlerin gelişimini yansıtan bir zaman dizisidir. Bu, belirleyici süreç anlamına gelen deterministik sürecin (veya deterministik sistemin) olasılıkçı muadilidir. Sadece tek yönlü olarak değişebilen bir süreci tasvir etmek yerine (örneğin, sıradan bir diferansiyel denklemin çözümünde olduğu gibi) bir stokastik veya rastgele süreçte, bazı belirsizlikler vardır. Hatta başlangıçtaki durum (veya başlangıç noktası) biliniyor olsa dahi sürecin gelişebileceği/değişebileceği bazı (çoğunlukla sonsuz) yönler vardır. Birçok stokastik süreçte, bir sonraki duruma veya konuma geçiş, yalnızca mevcut duruma bağlıdır ve işlemin önceki durumlarından veya değerlerinden bağımsızdır.
Ayrık zamanın basit formunda, sürekli zamanın aksine, stokastik süreç rastgele değişkenlerin bir dizilimidir. (Örneğin, ayrık zamanlı Markov zinciri olarak da bilinen Markov zincirine bakın.) Çeşitli zamanlara karşılık gelen rastgele değişkenler tamamen farklı olabilir, tek şart bu farklı rastgele niceliklerin hepsinin aynı uzayda değerler almasıdır (fonksiyonun değer kümesi). Bu rastgele değişkenleri bir veya birkaç deterministik argüman argümanın rastgele fonksiyonları olarak modellemek bir yaklaşım olabilir (çoğu durumda, zaman parametresi). Bir stokastik sürecin farklı zamanlardaki rastgele değerleri bağımsız rastgele değişken olabilse de, birçok genel olarak kabul görmüş durumda karmaşık istatistiksel bağımlılık sergiler.
Stokastik süreçlerin tanıdık örnekleri arasında borsa ve döviz kuru dalgalanmaları; Konuşma gibi sinyaller; Ses ve video; Bir hastanın EKG, EEG, kan basıncı ya da sıcaklığı gibi tıbbi veriler; ve Brown hareketi veya rastgele yürüyüşler gibi rastgele hareketi sayabiliriz.
Bir genelleme yaparsak, rastgele alan, değişkenlerin zaman yerine bir topolojik uzayın terimleri ile parametrelenmesine izin verilerek tanımlanır. Rastgele alanlara örnek olarak statik görüntüler, rastgele arazi (peyzaj), rüzgâr dalgaları ve heterojen bir malzemenin bileşim varyasyonları gösterilebilir.
Resmi tanım ve temel özellikler
Tanımı
Verilen bir olasılık kümesi 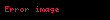
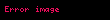


her 

Sonlu boyutsal dağılımlar
X, S değerli bir stokastik süreç olsun. Her sonlu sıralamada, 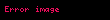

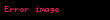

Uygun topolojik kısıtlamalar altında, bir stokastik süreci tanımlamak için uygun "tutarlı" sonlu boyutlu dağılım koleksiyonu kullanılabilir ("Yapı" bölümünde Kolmogorov eklentisine bakın).
Stokastik süreçlerin tarihçesi
Stokastik süreçler, ilk olarak 19. yüzyılın sonlarında finansal piyasalar ve Brown hareketini anlamaya yardımcı olmak için titizlikle incelenmiştir. Brown hareketinin matematiksel temelini ilk defa Thorvald N. Thiele, 1880'de yayınlanan en küçük kareler metodu üzerine yazdığı bir yazıda tanımlamıştır. Bunu, 1900'de diğer çalışmadan bağımsız olarak Louis Bachelier tarafından yazılan, hisse senedi ve opsiyon piyasalarının stokastik analizini sunduğu "Spekülasyon teorisi" doktora tezi izlemiştir. Bilgisayar destekli finansal karar alma modellerinin yaygınlaşmasıyla birlikte stokastik süreçler finansal piyasalarda en önemli çalışma alanı haline gelmiştir. Temelde brown hareketinin ya da random walk'ın statik analizi finansal kararlar için yetersizdir. Fiyatın nereye gideceği bilgisi portföy ve risk optimizasyonuna ilişkin bir bilgi vermez çünkü portföy riskleri birden fazla alım-satımın oluşturduğu birleşik bir süreçtir ve istatistiğin süreç disiplini olan stokastik analiz yöntemleriyle incelenebilir. Albert Einstein (1905 tarihli bir çalışmasında) ve Marian Smoluchowski (1906), sorunun çözümünü, atomlar ve moleküllerin varlığını dolaylı olarak doğrulamak için bir yol olarak fizikçilerin dikkatine sundular. Brown hareketini tanımlayan denklemleri daha sonra Jean Baptiste Perrin'in 1908'deki deneysel çalışmasıyla doğrulanmıştır. Einstein'ın makalesinden bir alıntı, bir stokastik modelin temellerini açıklıyor:
"Her partikülün diğer tüm parçacıkların hareketlerinden bağımsız bir hareketi gerçekleştirdiği açıkça görülmelidir; aynı zamanda, farklı zaman aralıklarında bir ve aynı parçacığın hareketleri zaman aralıkları çok küçük seçilmedikçe bağımsız hareketlerdir."
Gözlemlenebilir zaman aralıklarına kıyasla çok küçük olan bir zaman aralığı τ tanıtıyoruz, ancak yine de o kadar büyük ki, iki ardışık τ zaman aralığında, parçacık tarafından yürütülen hareketler birbirinden bağımsız olan olaylar olarak düşünülebilir ".
Yapılar
Ölçüm teorisi aracılığıyla olasılık teorisinin sıradan aksiyomazisyonunda sorun, tüm işlemlerin uzantısının ölçülebilir kısmının sigma cebirini inşa etmek ve sonra üstüne kesin bir ölçü koymaktır. Bu amaç için geleneksel bir şekilde kullanılan yöntem Kolmogorov uzantısı’dır.
Kolmogorov uzantısı
Kolmogorov uzantısı, aşağıdaki dizinler boyunca sürmektedir. Bütün işlemlerin uzantısı üstüne olasılık ölçümünü kabul edersek; 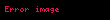
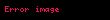
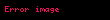
Kolmogorov uzantı teoremleri, Chapman−Kolmogorov işleyeblirlik koşulunu tatmin eden kesin boyutsal olasılık dağılımları verilen ailesi ile stokastik sürecin var oluşuna garanti eder.
Parçalanabilirlik ya da Kolmogorov uzantısının neyi sağlamadığı
Kolmogorov aksiomatizasyonunu hatırlarsak ölçüm setleri olasılık olan setlerdir ya da bir başka deyişle olasılıksal cevapları olan sorulara evet /hayır cevabı veren setlerdir. Kolmogorov uzantısı, 
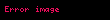
Ölçüm teorisinde eğer ölçülebilir setlerin koleksiyon sayısına sahipsek o halde hepsinin birleşim ve kesişimleri ölçülebilir settir. Amacımız için bu, olasılıksal cevabı olan sayılabilen birçok kordinata bağlı olan evet/hayır soruları anlamına gelir.
İyi haber şu ki Kolmogorov uzantısı oldukça izafi kesin boyutsal katkıları ile stokastik süreci olanaklı kılar. Hem de rastgele bir sıralama ile sorulduğunda, kişinin alabileceği yalnızca bir muhtemel cevap vardır. Kötü haber şu ki fonksiyonla ilgili net sorulara sürekli net olasılık cevabı yoktur. Kişi, fonksiyonla azıcık ilgili olan sayılamaz birçok değere bağlı sorular olduğunu ümit eder, ama gerçekten kötü haber şu ki neredeyse hesapların tüm konsepti bu türdür. Örneğin;
- Sınırsızlık
- Devamlılık
- Farklılaştırılabilirlik
Tamamı fonksiyonun birçok sayılamayan değerinin bilgisini gerektirir. Tek çözüm stokastik sürecin bölünmesini gerektirir.
Bir başka deyişle, birkaç sayılabilir koordinat vardırki seti 
Kolmogorov devam teoremleri, sürekli modifikasyonu olan artışlarının anları üzerine kesin zincirsel tahmini eden süreçleri garanti eder ve bundan dolayı bölünebilirler.
Filtrelemeler






Doğal filtreleme
Bir olasılık uzayı üzerinde tanımlanan 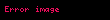
.
O zaman, 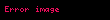
Sınıflandırma
Stokastik süreçler indeksin sıralamasına göre (genellikle zamansal) durumsal sınıflandırılabilirler.
Ayrı zaman ve ayrı durum uzantısı
Eğer 


- Eğer
aktarılan bitlerin sırasının
pozisyonunda bit (o ya da 1) ise, o zaman
iki durumlu Markov zinciri olarak modellenebilir. Bu data gönderimindeki hatayı düzeltir, virtebi algoritmasına yön verir.
- Eğer
doğurmayan bir model
th de doğuran bir çiftin genotip bileşimini sunar. Bu da gösterir ki nüfustaki heterojen bireysellerin oranı ∞’a giden
olarak eşitlenir.
Devam eden zaman ve devam eden durum uzantısı
Devam eden stokastik süreç paradigması, Wiener sürecidir. Asıl formunda problem, sıvı moleküllerinden sıvı yüzey üstünde yüzen vuruş alan parçacıkla ilgilidir. Parçacık o halde rastgele gücün öznesi, çünkü moleküller çok küçük ve birbirine yakın ve sürekli bu şekilde davranan olarak görülür ve çünkü parçacıklar yüzey basıncından sıvı yüzeyine zincirlidir ve zamanla yüzeye paralel taşıyıcı her noktadır. Böylece rastgele güç stokastik sürecin iki bileşenince tasvir edilir. İki gerçek-değerli rastgele çeşitler indeks setinde, zamanın (sıvı homojen bir güç olarak göründüğünden döngüsel koordinatlara bağlıdır.) R olarak iki rastgele çeşit alanı ile, gücün x ve y içeriklerini vererek ilintilidir. Genellikle Brownian hareket tarzı hem de Langevin eşitliği olarak bilinen bir hareket eşitliği ile sonuçlanan yapışkan sıvı etkisini içerir.
Ayrı zaman ve devam eden durum uzantısı
Eğer indeks süreç seti N(doğal sayılar) ve çeşit R(gerçel sayılar) ise örnek dizinin {Xi}i ∈ N olduğu yer olan {Xi(ω)}i ∈ N sürecinin örnek dizini hakkında sorulan birkaç doğal soru vardır.
- Her bir örneğin sınırlandırma olasılığı nedir?
- Her örneğin monoton dizileri olasılığı nedir?
- her örneğin indeks yaklaşımları ∞ olarak limitinin olasılığı nedir?
yakınsaması her örneğinden elde edilen diziler olasılığı nedir?
- Matematik probleminin katkı olasılığı nedir?
Ayrı zaman devam eden durum stokastik modelin esas uygulaması Markov zinciri Monte Carlo (MCMC)’yi ve zaman dizinlerinin analizini içerir.
Devam eden zaman ve ayrı durum uzantısı
Benzer olarak, eğer indeks uzantısı I kesin ya da kesin olmayan aralık ise {Xt(ω)}t ∈ I örnek patikası hakkında soru sorabiliriz.
- Sınırlandırılmış/tümlevnebilir olma olasılığı nedir?
- ∞ limiti olma olasılığı nedir?
- İntegral katkı olasılığı nedir?
İlave Kaynaklar
- Wio, S. Horacio, Deza, R. Roberto & Lopez, M. Juan (2012). An Introduction to Stochastic Processes and Nonequilibrium Statistical Physics. World Scientific Publishing. ISBN .
- Papoulis, Athanasios; Pillai, S. Unnikrishna (2001). Probability, Random Variables and Stochastic Processes. McGraw-Hill Science/Engineering/Math. ISBN .
- . "Lecture notes in Advanced probability theory". 28 Kasım 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- Doob, J. L. (1953). Stochastic Processes. Wiley.
- Klebaner, Fima C. (2011). Introduction to Stochastic Calculus With Applications. Imperial College Press. ISBN .
- Bruce Hajek (Temmuz 2006). "An Exploration of Random Processes for Engineers". 17 Nisan 2009 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- "An 8 foot tall Probability Machine (named Sir Francis) comparing stock market returns to the randomness of the beans dropping through the quincunx pattern". Index Funds Advisors. 17 Ocak 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- "Popular Stochastic Processes used in Quantitative Finance". sitmo.com. 30 Aralık 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- "Interactive Web Application: Stochastic Processes used in Quantitative Finance". TuringFinance.com. 20 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- "Addressing Risk and Uncertainty". 23 Ağustos 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2016.
- "Stokastik Süreçlere Giriş". 30 Ocak 2023 tarihinde kaynağından arşivlendi.
Kaynakça
- ^ Dodge, Yadolah (2006). The Oxford Dictionary of Statistical Terms. Oxford, England: Oxford University Press. s. 335. ISBN .
- ^ Lindsey, J. K. (2004). Statistical Analysis of Stochastic Processes in Time. Cambridge, England: Cambridge University Press. ss. 3. ISBN .
- ^ (2006). Introduction to Stochastic processes (2 bas.). CRC Press. s. 1. 7 Nisan 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ocak 2017.
A stochastic process is a random process evolving with time. More precisely, a stochastic process is a collection of random variables
indexed by time.
- ^ "Trading Modellerinde Stokastik Süreç Neden Olasılıktan Daha Önemli". Datakapital. 5 Mart 2021. 1 Nisan 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Mart 2021.
- ^ Einstein, Albert (1926). "Investigations on the Theory of the Brownian Movement" (PDF). 15 Şubat 2017 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 3 Ocak 2017.
- ^ Karlin, Samuel & Taylor, Howard M. (1998). An Introduction to Stochastic Modeling, Academic Press. .
- ^ Allen, Linda J. S., An Introduction to Stochastic Processes with Applications to Biology, 2nd Edition, Chapman and Hall, 2010,
- ^ Gardiner, C. Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences, 3rd ed., Springer, 2004,
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Stokastik surec Stokastik islemi veya rastgele surec zaman veya mekana gore degisen evrilen olgulari tanimlamak icin kullanilan bir olasilik modelidir Daha kapsamli olarak olasilik teorisinde stokastik surec degisimi rastgele bir varyasyona bagli olan bir degisken tarafindan temsil edilen bazi sistemlerin gelisimini yansitan bir zaman dizisidir Bu belirleyici surec anlamina gelen deterministik surecin veya deterministik sistemin olasilikci muadilidir Sadece tek yonlu olarak degisebilen bir sureci tasvir etmek yerine ornegin siradan bir diferansiyel denklemin cozumunde oldugu gibi bir stokastik veya rastgele surecte bazi belirsizlikler vardir Hatta baslangictaki durum veya baslangic noktasi biliniyor olsa dahi surecin gelisebilecegi degisebilecegi bazi cogunlukla sonsuz yonler vardir Bircok stokastik surecte bir sonraki duruma veya konuma gecis yalnizca mevcut duruma baglidir ve islemin onceki durumlarindan veya degerlerinden bagimsizdir Ayrik zamanin basit formunda surekli zamanin aksine stokastik surec rastgele degiskenlerin bir dizilimidir Ornegin ayrik zamanli Markov zinciri olarak da bilinen Markov zincirine bakin Cesitli zamanlara karsilik gelen rastgele degiskenler tamamen farkli olabilir tek sart bu farkli rastgele niceliklerin hepsinin ayni uzayda degerler almasidir fonksiyonun deger kumesi Bu rastgele degiskenleri bir veya birkac deterministik arguman argumanin rastgele fonksiyonlari olarak modellemek bir yaklasim olabilir cogu durumda zaman parametresi Bir stokastik surecin farkli zamanlardaki rastgele degerleri bagimsiz rastgele degisken olabilse de bircok genel olarak kabul gormus durumda karmasik istatistiksel bagimlilik sergiler Stokastik sureclerin tanidik ornekleri arasinda borsa ve doviz kuru dalgalanmalari Konusma gibi sinyaller Ses ve video Bir hastanin EKG EEG kan basinci ya da sicakligi gibi tibbi veriler ve Brown hareketi veya rastgele yuruyusler gibi rastgele hareketi sayabiliriz Bir genelleme yaparsak rastgele alan degiskenlerin zaman yerine bir topolojik uzayin terimleri ile parametrelenmesine izin verilerek tanimlanir Rastgele alanlara ornek olarak statik goruntuler rastgele arazi peyzaj ruzgar dalgalari ve heterojen bir malzemenin bilesim varyasyonlari gosterilebilir Resmi tanim ve temel ozelliklerTanimi Verilen bir olasilik kumesi W F P displaystyle Omega mathcal F P ve olcumlenebilir bir kumede S S displaystyle S Sigma S degerli bir stokastik surec W displaystyle Omega daki S degerli rastgele degiskenlerin toplami tamamen T zaman ile endekslenmis toplamidir Bir stokastik X sureci Xt t T displaystyle X t t in T her Xt displaystyle X t nin W displaystyle Omega icinde S degerli bir rastgele degisken oldugu bir toplamdir S kumesi bundan sonra islemin durum kumesi olarak adlandirilir Sonlu boyutsal dagilimlar X S degerli bir stokastik surec olsun Her sonlu siralamada T t1 tk Tk displaystyle T t 1 ldots t k in T k k degiskenler grubu XT Xt1 Xt2 Xtk displaystyle X T X t 1 X t 2 ldots X t k PT P XT 1 displaystyle mathbb P T cdot mathbb P X T 1 cdot Sk displaystyle S k daki degerleri alan bir rastgele degiskendir Buna X in sonlu boyutsal dagilimi denir Uygun topolojik kisitlamalar altinda bir stokastik sureci tanimlamak icin uygun tutarli sonlu boyutlu dagilim koleksiyonu kullanilabilir Yapi bolumunde Kolmogorov eklentisine bakin Stokastik sureclerin tarihcesiStokastik surecler ilk olarak 19 yuzyilin sonlarinda finansal piyasalar ve Brown hareketini anlamaya yardimci olmak icin titizlikle incelenmistir Brown hareketinin matematiksel temelini ilk defa Thorvald N Thiele 1880 de yayinlanan en kucuk kareler metodu uzerine yazdigi bir yazida tanimlamistir Bunu 1900 de diger calismadan bagimsiz olarak Louis Bachelier tarafindan yazilan hisse senedi ve opsiyon piyasalarinin stokastik analizini sundugu Spekulasyon teorisi doktora tezi izlemistir Bilgisayar destekli finansal karar alma modellerinin yayginlasmasiyla birlikte stokastik surecler finansal piyasalarda en onemli calisma alani haline gelmistir Temelde brown hareketinin ya da random walk in statik analizi finansal kararlar icin yetersizdir Fiyatin nereye gidecegi bilgisi portfoy ve risk optimizasyonuna iliskin bir bilgi vermez cunku portfoy riskleri birden fazla alim satimin olusturdugu birlesik bir surectir ve istatistigin surec disiplini olan stokastik analiz yontemleriyle incelenebilir Albert Einstein 1905 tarihli bir calismasinda ve Marian Smoluchowski 1906 sorunun cozumunu atomlar ve molekullerin varligini dolayli olarak dogrulamak icin bir yol olarak fizikcilerin dikkatine sundular Brown hareketini tanimlayan denklemleri daha sonra Jean Baptiste Perrin in 1908 deki deneysel calismasiyla dogrulanmistir Einstein in makalesinden bir alinti bir stokastik modelin temellerini acikliyor Her partikulun diger tum parcaciklarin hareketlerinden bagimsiz bir hareketi gerceklestirdigi acikca gorulmelidir ayni zamanda farkli zaman araliklarinda bir ve ayni parcacigin hareketleri zaman araliklari cok kucuk secilmedikce bagimsiz hareketlerdir Gozlemlenebilir zaman araliklarina kiyasla cok kucuk olan bir zaman araligi t tanitiyoruz ancak yine de o kadar buyuk ki iki ardisik t zaman araliginda parcacik tarafindan yurutulen hareketler birbirinden bagimsiz olan olaylar olarak dusunulebilir YapilarOlcum teorisi araciligiyla olasilik teorisinin siradan aksiyomazisyonunda sorun tum islemlerin uzantisinin olculebilir kisminin sigma cebirini insa etmek ve sonra ustune kesin bir olcu koymaktir Bu amac icin geleneksel bir sekilde kullanilan yontem Kolmogorov uzantisi dir Kolmogorov uzantisi Kolmogorov uzantisi asagidaki dizinler boyunca surmektedir Butun islemlerin uzantisi ustune olasilik olcumunu kabul edersek f X Y displaystyle f X to Y var olur sonra kesin boyutsal olasiliginin rastgele cesitlere baglantisini ozellestirmek icin f x1 f xn displaystyle f x 1 dots f x n kullanilir Simdi n boyutsal katkisindan f x1 f xn 1 displaystyle f x 1 dots f x n 1 icin n 1 boyutsal marjinal boyutsal katkisini cikarabiliriz Acikca isleyebilirlik boyutuna dikkat edelim ki ismen bu marjinal olasilik katkisi tam sisimis stokastik surecten gelen olarak ayni siniftadir bir gereksinim degildir Eger stokastik surec Wiener sureciyse ki olay alan marjinaller artis sinifinin tum gaussca katkilaridir ama butun stokastik surecler icin genel degildir sadece bu gibi kosullarda elde dilir Bu kosul olasilik yogunlugu acisindan aciklandiginda sonuc Chapman Kolmogorov esitligi olarak adlandirilir Kolmogorov uzanti teoremleri Chapman Kolmogorov isleyeblirlik kosulunu tatmin eden kesin boyutsal olasilik dagilimlari verilen ailesi ile stokastik surecin var olusuna garanti eder Parcalanabilirlik ya da Kolmogorov uzantisinin neyi saglamadigi Kolmogorov aksiomatizasyonunu hatirlarsak olcum setleri olasilik olan setlerdir ya da bir baska deyisle olasiliksal cevaplari olan sorulara evet hayir cevabi veren setlerdir Kolmogorov uzantisi Yn displaystyle Y n nin olculebilir kisimlarinda yatmaya kisitlanan kesin bircok koordinatin bulundugu yerde f x1 f xn displaystyle f x 1 dots f x n fonksiyonlarinin butun olculebilir setlerinin bildirimiyle baslar Diger bir deyisle bircok koordinatin cogundaki degerlere bakilarak f ile ilgili evet hayir cevabi verilebilinirse o zaman O olasilik cevabi olur Olcum teorisinde eger olculebilir setlerin koleksiyon sayisina sahipsek o halde hepsinin birlesim ve kesisimleri olculebilir settir Amacimiz icin bu olasiliksal cevabi olan sayilabilen bircok kordinata bagli olan evet hayir sorulari anlamina gelir Iyi haber su ki Kolmogorov uzantisi oldukca izafi kesin boyutsal katkilari ile stokastik sureci olanakli kilar Hem de rastgele bir siralama ile soruldugunda kisinin alabilecegi yalnizca bir muhtemel cevap vardir Kotu haber su ki fonksiyonla ilgili net sorulara surekli net olasilik cevabi yoktur Kisi fonksiyonla azicik ilgili olan sayilamaz bircok degere bagli sorular oldugunu umit eder ama gercekten kotu haber su ki neredeyse hesaplarin tum konsepti bu turdur Ornegin Sinirsizlik Devamlilik Farklilastirilabilirlik Tamami fonksiyonun bircok sayilamayan degerinin bilgisini gerektirir Tek cozum stokastik surecin bolunmesini gerektirir Bir baska deyisle birkac sayilabilir koordinat vardirki seti f xi displaystyle f x i degerleri butun f in rastgele fonksiyonlarini belirtir Kolmogorov devam teoremleri surekli modifikasyonu olan artislarinin anlari uzerine kesin zincirsel tahmini eden surecleri garanti eder ve bundan dolayi bolunebilirler Filtrelemeler W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi ve T R displaystyle T subset mathbb R olsun Eger bir s cebiri ailesi Ft t T displaystyle mathcal F t t in T icin Fs Ft F s t s t T displaystyle mathcal F s subset mathcal F t subset mathcal F forall s leq t s t in T saglaniyorsa Ft t T displaystyle mathcal F t t in T ye W F P displaystyle Omega mathcal F mathbb P olasilik uzayinin bir filtrelemesi ya da suzgeci denir Dogal filtreleme Bir olasilik uzayi uzerinde tanimlanan Xt t T displaystyle X t t in T rassal sureci icin asagidaki gibi bir ailesi tanimlansin FtX s Xs s t s T t T displaystyle mathcal F t X sigma X s mid s leq t s in T quad t in T O zaman FtX t T displaystyle left mathcal F t X right t in T bir filtreleme olur ve buna Xt t T displaystyle X t t in T rassal surecinin dogal filtrelemesi denir SiniflandirmaStokastik surecler indeksin siralamasina gore genellikle zamansal durumsal siniflandirilabilirler Ayri zaman ve ayri durum uzantisi Eger t displaystyle t ve Xt displaystyle X t nin her ikisi de N displaystyle mathbb N dogal sayilar seti ye aitse o zaman Markov zincirlerine yon veren modellere sahibizdir Eger Xt displaystyle X t aktarilan bitlerin sirasinin t displaystyle t pozisyonunda bit o ya da 1 ise o zaman Xt displaystyle X t iki durumlu Markov zinciri olarak modellenebilir Bu data gonderimindeki hatayi duzeltir virtebi algoritmasina yon verir Eger Xt displaystyle X t dogurmayan bir model t displaystyle t th de doguran bir ciftin genotip bilesimini sunar Bu da gosterir ki nufustaki heterojen bireysellerin orani a giden t displaystyle t olarak esitlenir Devam eden zaman ve devam eden durum uzantisi Devam eden stokastik surec paradigmasi Wiener surecidir Asil formunda problem sivi molekullerinden sivi yuzey ustunde yuzen vurus alan parcacikla ilgilidir Parcacik o halde rastgele gucun oznesi cunku molekuller cok kucuk ve birbirine yakin ve surekli bu sekilde davranan olarak gorulur ve cunku parcaciklar yuzey basincindan sivi yuzeyine zincirlidir ve zamanla yuzeye paralel tasiyici her noktadir Boylece rastgele guc stokastik surecin iki bilesenince tasvir edilir Iki gercek degerli rastgele cesitler indeks setinde zamanin sivi homojen bir guc olarak gorundugunden dongusel koordinatlara baglidir R olarak iki rastgele cesit alani ile gucun x ve y iceriklerini vererek ilintilidir Genellikle Brownian hareket tarzi hem de Langevin esitligi olarak bilinen bir hareket esitligi ile sonuclanan yapiskan sivi etkisini icerir Ayri zaman ve devam eden durum uzantisi Eger indeks surec seti N dogal sayilar ve cesit R gercel sayilar ise ornek dizinin Xi i N oldugu yer olan Xi w i N surecinin ornek dizini hakkinda sorulan birkac dogal soru vardir Her bir ornegin sinirlandirma olasiligi nedir Her ornegin monoton dizileri olasiligi nedir her ornegin indeks yaklasimlari olarak limitinin olasiligi nedir f i displaystyle f i yakinsamasi her orneginden elde edilen diziler olasiligi nedir Matematik probleminin katki olasiligi nedir Ayri zaman devam eden durum stokastik modelin esas uygulamasi Markov zinciri Monte Carlo MCMC yi ve zaman dizinlerinin analizini icerir Devam eden zaman ve ayri durum uzantisi Benzer olarak eger indeks uzantisi I kesin ya da kesin olmayan aralik ise Xt w t I ornek patikasi hakkinda soru sorabiliriz Sinirlandirilmis tumlevnebilir olma olasiligi nedir limiti olma olasiligi nedir Integral katki olasiligi nedir Ilave Kaynaklar Wio S Horacio Deza R Roberto amp Lopez M Juan 2012 An Introduction to Stochastic Processes and Nonequilibrium Statistical Physics World Scientific Publishing ISBN 978 981 4374 78 1 KB1 bakim Birden fazla ad yazar listesi link Papoulis Athanasios Pillai S Unnikrishna 2001 Probability Random Variables and Stochastic Processes McGraw Hill Science Engineering Math ISBN 0 07 281725 9 Lecture notes in Advanced probability theory 28 Kasim 2008 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 Doob J L 1953 Stochastic Processes Wiley Klebaner Fima C 2011 Introduction to Stochastic Calculus With Applications Imperial College Press ISBN 1 84816 831 4 Bruce Hajek Temmuz 2006 An Exploration of Random Processes for Engineers 17 Nisan 2009 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 An 8 foot tall Probability Machine named Sir Francis comparing stock market returns to the randomness of the beans dropping through the quincunx pattern Index Funds Advisors 17 Ocak 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 Popular Stochastic Processes used in Quantitative Finance sitmo com 30 Aralik 2016 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 Interactive Web Application Stochastic Processes used in Quantitative Finance TuringFinance com 20 Eylul 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 Addressing Risk and Uncertainty 23 Agustos 2010 tarihinde kaynagindan arsivlendi Erisim tarihi 29 Aralik 2016 Stokastik Sureclere Giris 30 Ocak 2023 tarihinde kaynagindan arsivlendi Kaynakca Dodge Yadolah 2006 The Oxford Dictionary of Statistical Terms Oxford England Oxford University Press s 335 ISBN 9780199206131 Lindsey J K 2004 Statistical Analysis of Stochastic Processes in Time Cambridge England Cambridge University Press ss 3 ISBN 9780521837415 2006 Introduction to Stochastic processes 2 bas CRC Press s 1 7 Nisan 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 3 Ocak 2017 A stochastic process is a random process evolving with time More precisely a stochastic process is a collection of random variables Xt displaystyle X t indexed by time Trading Modellerinde Stokastik Surec Neden Olasiliktan Daha Onemli Datakapital 5 Mart 2021 1 Nisan 2021 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Mart 2021 Einstein Albert 1926 Investigations on the Theory of the Brownian Movement PDF 15 Subat 2017 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 3 Ocak 2017 Karlin Samuel amp Taylor Howard M 1998 An Introduction to Stochastic Modeling Academic Press ISBN 0 12 684887 4 Allen Linda J S An Introduction to Stochastic Processes with Applications to Biology 2nd Edition Chapman and Hall 2010 ISBN 1 4398 1882 7 Gardiner C Handbook of Stochastic Methods for Physics Chemistry and the Natural Sciences 3rd ed Springer 2004 ISBN 3540208828
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans