Matematikte çapraz çarpım veya yöney çarpımı üç boyutlu uzayda iki yöney (vektör) ile yapılan bir işlemdir. Bu çarpımın sonucunda başka bir yöney elde edilir ve bu yöney çapraz çarpımda kullanılan iki yöneye de diktir. Aynı zamanda elde edilen yöney çapraz çarpımda kullanılan iki yöneyin oluşturduğu düzleme dik bir yöneydir. Bu çarpımın çapraz ismi gösterimde kullanılan "×" sembolünden gelmektedir ve her bir vektör sıralı bir şekilde diğeri ile çarpılmakta ve elde edilen yöney bu çarpan yöneylerden biri olmaktadır,yani çaprazlama yapılan modüler bir çarpım biçimidir.Yöney çarpımı ismi de işlemin sonucunda başka bir yöneyin elde edilmesinden gelmektedir. Bu işlemin matematik, fizik ve mühendislikte birçok uygulaması vardır.

Tanım

a ve b ile gösterilen iki yöneyin çapraz çarpımı a × b şeklinde gösterilir. Fizikte bazen çapraz çarpım a ∧ b şeklinde de gösterilir ama bu gösterim matematikte başka kullanımlarla karıştırılmaması için kullanılmaz.
a × b çapraz çarpımı c yöneyi ile tanımlanabilir ve bu c yöneyinin a ve b yöneylerine dik olması gerekmektedir. Ayrıca c yöneyinin yönü sağ el kuralı ile belirlenmelidir. c yöneyinin boyu ise a ve b yöneyi kullanılarak elde edilen paralelkenarın alanına eşittir.
Çapraz çarpım aşağıdaki denklem ile tanımlanır:
burada θ a ve b yöneyi arasında kalan ve 180°'den küçük olan açıdır. (0° ≤ θ ≤ 180°), a ve b; a ve b yöneylerinin boylarına karşılık gelmektedir (a = |a| ve b = |b|) ve n yöneyi a ve b'nin oluşturduğu yüzeye dikme olan birim yöneydir ve yönü sağ el kuralı kullanılarak bulunur. Eğer a ve b parallelse (ikisinin arasındaki açı θ, 0° veya 180° ise), yukarıdaki denklemden yola çıktığımızda a ve b'nin çapraz çarpımının 0 (sıfır) olduğunu görürüz.
n birim yöneyinin yönü sağ el kuralı ile bulunur; çapraz çarpımdaki ilk yöney a doğrultusunda işaret parmağımızı, çapraz çarpımdaki ikinci yöney b doğrultusunda orta parmağımızı uzattığımızda başparmağımızın yönü n birim yöneyinin yönünü gösterir. Parmakların yönelimi ve yöneylerin doğrultusu yandaki çizimde gösterilmiştir. Çapraz çarpımda, çarpımda kullanılan iki yöneyin yerleri değiştirilirse sonucun ilk işlemde elde edilen sonucun eksi işaretlisi olduğu görülür ve bu olarak tanımlanır ve bu durum matematiksel olarak b × a = −(a × b) şeklinde gösterilir.
En başta tanımlanırken de belirtildiği üzere sağ elli mi sol elli mi koordinat sisteminin kullanıldığı önemlidir. Yukarıda belirtildiği şekilde n birim yöneyinin yönü sağ elli koordinat sisteminde sağ el kuralı kullanılarak bulunmuştur. Eğer sol elli bir koordinat sistemi kullanılsaydı o zaman da sağ el kullanılarak yapılan işlemin sol el kullanılarak yapılması gerekirdi ve n birim yöneyinin yönü bulunmuş olurdu.
Ayna yansıması kullanılarak elde edilen sistemde bu durum sorun yaratmaktadır. Bir yöneyin yönü ayna yansıması düşünüldüğünde olarak kalmalıdır. Ama ayna yansıması şeklinde elde edilen koordinat sistemi sol ellidir ve çapraz çarpım düşünüldüğünde elde edilen sonucun yönü tersine döner. Bu durum yöneylerin ayna yansımasının düşünülmesi durumuyla uyuşmamaktadır. Bu uyuşmazlık çapraz çarpımla elde edilen yöneylerin yalancıyöney (pseudovector) olarak tanımlanması ile çözümlenmiştir.
Çapraz çarpımın hesaplanması
Koordinat gösterimi
Kartezyen koordinat sisteminin birim yöneyleri i, j ve k için aşağıdaki özellikler tanımlanır:
Bu tanımlamalar ve çapraz çarpımın özellikleri kullanılarak aşağıdaki denklemler elde edilir:
.
Bunlar kullanılarak da herhangi a = a1i + a2j + a3k ve b = b1i + b2j + b3k şeklinde yazılan iki yöney için çapraz çarpım aşağıdaki gibi hesaplanır:
Bu sonuç yöneylerin kolon şeklindeki gösterimi kullanılarak da aşağıdaki gibi yazılabilir:
Dizey gösterimi
Çapraz çarpım bir dizeyin belirtkeni (determinantı) ile de gösterilebilir:
Bu belirtken Sarrus kuralı veya Laplace açılımı ile hesaplanabilir.
Sarrus kuralı ile yazdığımızda
açılımı elde ederiz.
Laplace açılımı ile en üsteki satırı kullanarak
yazımını elde ederiz. Burada ikili kare dizeylerin tekrar belirtkeni hesaplanmalıdır.
Özellikleri
Geometrik anlamı


Çapraz çarpımın büyüklüğü a ve b yöneylerinin paralelkenara tamamlanarak elde edilen paralelkenarın alanına eşittir ve aşağıdaki şekilde gösterilir (Şekil 1):
Yukarıdaki denklemden de görüleceği üzere büyüklüğü yazarken iki yöneyin arasında kalan açının sinüsü kullanılmıştır. b yöneyi ile Şekil 1 de gösterilen açının sinüsünün çarpımını düşünelim
Bu çarpım b yöneyinin a yöneyine dik olan bileşenini verir. Birbirine dik olan iki yöneyin büyüklüklerinin çarpımı da o yöneyler kullanılarak elde edilen paralelkenarın alanını verir.
Eğer iki yöneyimiz de birbirine dik ise (arada kalan açı 90 derece) sinüs ifadesi 1'e eşittir ve iki yöneyin büyüklüklerinin çarpımı oluşan diktörtgenin alanına eşittir.
a, b ve c yöneylerinden oluşturulan pirizmanın oylumu (hacmi) da bir çapraz çarpım bir de nokta çarpım ile bulunabilir (Şekil 2) ve aşağıdaki şekilde yazılır:
Burada dikkat edilmesi gereken bu üçlü çarpımın sonucunun eksi olabileceğidir ve oylumun büyüklüğü daima artı değere sahip olacağı için oylum
şeklinde gösterilir.
İşlem özellikleri
Çarpraz çarpım eksi yerdeğiştirme özelliğine sahiptir,
toplama üzerine dağılma özelliğine sahiptir,
ve bir sayıl ile çarpılması aşağıdaki gibidir
Birleşme özelliğine sahip değildir. Diğer taraftan, Jakobi özdeşliği ile üçlü çapraz çarpımda sıra değiştirme işlemi yapılabilir:
Çapraz çarpımda sadeleştirme işlemi yapılmaz: a × b = a × c ise, a yöneyi sıfırdan farklı olduğu durumlarda b = c koşulu zorunlu değildir. Bazı durumlarda b = c olsa bile, her durumda olmak zorunda değildir. Bunun yerine a × b = a × c olduğu durumda aşağıdaki işlem gerçekleştirilebilir:
Yukarıdaki işlemde, a veya b - c sıfırdan farklı ise a ve b - c arasındaki açı sıfırdır. Açı sıfır ise de birbirlerine ya paraleldirler ya da antiparaleldirler.
Uzam (geometrik) tanımı düşünüldüğünde a × b çapraz çarpımı, a × b işlemi sonucu elde edilen yeni yöney etrafında dönderildiğinde sonuçta herhangi bir değişim olmaz. Bu duruma benzer bir durum, 
yukarıdaki yazımda 
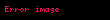


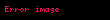


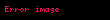



İki yöneyin çapraz çarpımı, 3 boyutlu uzayda daima iki yöney kullanılarak yazılan sütun şeklindeki dizeyin boşuzayındadır. Bu durum aşağıdaki şekilde gösterilir:
İki çapraz çarpımın toplamı için aşağıdaki özdeşlik geçerlidir:
Ayrıca bakınız
- – iki kümenin bir çarpımı
- Nokta çarpım
- – üç vektörden daha fazla çarpım içeriyor
- × (sembolü)
Notlar
Kaynakça
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. s. 134. ISBN .
- (1948) , Chapter 2: Vector Product, pp 11 –31, London: Methuen Publishing.
- Wilson, Edwin Bidwell (1901). Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. .
Dış bağlantılar
- Hazewinkel, Michiel, (Ed.) (2001), "Cross product", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- Eric W. Weisstein, Cross Product (MathWorld)
- A quick geometrical derivation and interpretation of cross products25 Haziran 2010 tarihinde Wayback Machine sitesinde .
- Z.K. Silagadze (2002). Multi-dimensional vector product. Journal of Physics. A35, 4949 5 Eylül 2015 tarihinde Wayback Machine sitesinde . (it is only possible in 7-D space)
- Real and Complex Products of Complex Numbers 8 Temmuz 2014 tarihinde Wayback Machine sitesinde .
- created at Syracuse University - (requires )
- W. Kahan (2007). Cross-Products and Rotations in Euclidean 2- and 3-Space. University of California, Berkeley (PDF). 10 Eylül 2014 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte capraz carpim veya yoney carpimi uc boyutlu uzayda iki yoney vektor ile yapilan bir islemdir Bu carpimin sonucunda baska bir yoney elde edilir ve bu yoney capraz carpimda kullanilan iki yoneye de diktir Ayni zamanda elde edilen yoney capraz carpimda kullanilan iki yoneyin olusturdugu duzleme dik bir yoneydir Bu carpimin capraz ismi gosterimde kullanilan sembolunden gelmektedir ve her bir vektor sirali bir sekilde digeri ile carpilmakta ve elde edilen yoney bu carpan yoneylerden biri olmaktadir yani caprazlama yapilan moduler bir carpim bicimidir Yoney carpimi ismi de islemin sonucunda baska bir yoneyin elde edilmesinden gelmektedir Bu islemin matematik fizik ve muhendislikte bircok uygulamasi vardir Sag elli koordinat sisteminde capraz carpim TanimCapraz carpimin sonucunda elde edilen yoneyin yonunun sag el kurali ile bulunmasi a ve b ile gosterilen iki yoneyin capraz carpimi a b seklinde gosterilir Fizikte bazen capraz carpim a b seklinde de gosterilir ama bu gosterim matematikte baska kullanimlarla karistirilmamasi icin kullanilmaz a b capraz carpimi c yoneyi ile tanimlanabilir ve bu c yoneyinin a ve b yoneylerine dik olmasi gerekmektedir Ayrica c yoneyinin yonu sag el kurali ile belirlenmelidir c yoneyinin boyu ise a ve b yoneyi kullanilarak elde edilen paralelkenarin alanina esittir Capraz carpim asagidaki denklem ile tanimlanir a b absin 8 n displaystyle mathbf a times mathbf b ab sin theta mathbf n burada 8 a ve b yoneyi arasinda kalan ve 180 den kucuk olan acidir 0 8 180 a ve b a ve b yoneylerinin boylarina karsilik gelmektedir a a ve b b ve n yoneyi a ve b nin olusturdugu yuzeye dikme olan birim yoneydir ve yonu sag el kurali kullanilarak bulunur Eger a ve b parallelse ikisinin arasindaki aci 8 0 veya 180 ise yukaridaki denklemden yola ciktigimizda a ve b nin capraz carpiminin 0 sifir oldugunu goruruz n birim yoneyinin yonu sag el kurali ile bulunur capraz carpimdaki ilk yoney a dogrultusunda isaret parmagimizi capraz carpimdaki ikinci yoney b dogrultusunda orta parmagimizi uzattigimizda basparmagimizin yonu n birim yoneyinin yonunu gosterir Parmaklarin yonelimi ve yoneylerin dogrultusu yandaki cizimde gosterilmistir Capraz carpimda carpimda kullanilan iki yoneyin yerleri degistirilirse sonucun ilk islemde elde edilen sonucun eksi isaretlisi oldugu gorulur ve bu olarak tanimlanir ve bu durum matematiksel olarak b a a b seklinde gosterilir En basta tanimlanirken de belirtildigi uzere sag elli mi sol elli mi koordinat sisteminin kullanildigi onemlidir Yukarida belirtildigi sekilde n birim yoneyinin yonu sag elli koordinat sisteminde sag el kurali kullanilarak bulunmustur Eger sol elli bir koordinat sistemi kullanilsaydi o zaman da sag el kullanilarak yapilan islemin sol el kullanilarak yapilmasi gerekirdi ve n birim yoneyinin yonu bulunmus olurdu Ayna yansimasi kullanilarak elde edilen sistemde bu durum sorun yaratmaktadir Bir yoneyin yonu ayna yansimasi dusunuldugunde olarak kalmalidir Ama ayna yansimasi seklinde elde edilen koordinat sistemi sol ellidir ve capraz carpim dusunuldugunde elde edilen sonucun yonu tersine doner Bu durum yoneylerin ayna yansimasinin dusunulmesi durumuyla uyusmamaktadir Bu uyusmazlik capraz carpimla elde edilen yoneylerin yalanciyoney pseudovector olarak tanimlanmasi ile cozumlenmistir Capraz carpimin hesaplanmasiKoordinat gosterimi Kartezyen koordinat sisteminin birim yoneyleri i j ve k icin asagidaki ozellikler tanimlanir i j k j k i k i j displaystyle mathbf i times mathbf j mathbf k quad mathbf j times mathbf k mathbf i quad mathbf k times mathbf i mathbf j Bu tanimlamalar ve capraz carpimin ozellikleri kullanilarak asagidaki denklemler elde edilir j i k k j i i k j displaystyle mathbf j times mathbf i mathbf k quad mathbf k times mathbf j mathbf i quad mathbf i times mathbf k mathbf j i i j j k k 0 displaystyle mathbf i times mathbf i mathbf j times mathbf j mathbf k times mathbf k mathbf 0 Bunlar kullanilarak da herhangi a a1i a2j a3k ve b b1i b2j b3k seklinde yazilan iki yoney icin capraz carpim asagidaki gibi hesaplanir a b a1i a2j a3k b1i b2j b3k a1b1i i a1b2i j a1b3i k a2b1j i a2b2j j a2b3j k a3b1k i a3b2k j a3b3k k a1b10 a1b2k a1b3 j a2b1 k a2b20 a2b3i a3b1j a3b2 i a3b30 a2b3 a3b2 i a3b1 a1b3 j a1b2 a2b1 k displaystyle begin aligned mathbf a times mathbf b amp a 1 mathbf i a 2 mathbf j a 3 mathbf k times b 1 mathbf i b 2 mathbf j b 3 mathbf k amp a 1 b 1 mathbf i times mathbf i a 1 b 2 mathbf i times mathbf j a 1 b 3 mathbf i times mathbf k amp a 2 b 1 mathbf j times mathbf i a 2 b 2 mathbf j times mathbf j a 2 b 3 mathbf j times mathbf k amp a 3 b 1 mathbf k times mathbf i a 3 b 2 mathbf k times mathbf j a 3 b 3 mathbf k times mathbf k amp a 1 b 1 mathbf 0 a 1 b 2 mathbf k a 1 b 3 mathbf j a 2 b 1 mathbf k a 2 b 2 mathbf 0 a 2 b 3 mathbf i a 3 b 1 mathbf j a 3 b 2 mathbf i a 3 b 3 mathbf 0 amp a 2 b 3 a 3 b 2 mathbf i a 3 b 1 a 1 b 3 mathbf j a 1 b 2 a 2 b 1 mathbf k end aligned Bu sonuc yoneylerin kolon seklindeki gosterimi kullanilarak da asagidaki gibi yazilabilir a1a2a3 b1b2b3 a2b3 a3b2a3b1 a1b3a1b2 a2b1 displaystyle begin pmatrix a 1 a 2 a 3 end pmatrix times begin pmatrix b 1 b 2 b 3 end pmatrix begin pmatrix a 2 b 3 a 3 b 2 a 3 b 1 a 1 b 3 a 1 b 2 a 2 b 1 end pmatrix Dizey gosterimi Capraz carpim bir dizeyin belirtkeni determinanti ile de gosterilebilir a b ijka1a2a3b1b2b3 displaystyle mathbf a times mathbf b begin vmatrix mathbf i amp mathbf j amp mathbf k a 1 amp a 2 amp a 3 b 1 amp b 2 amp b 3 end vmatrix Bu belirtken Sarrus kurali veya Laplace acilimi ile hesaplanabilir Sarrus kurali ile yazdigimizda a b ia2b3 ja3b1 ka1b2 ia3b2 ja1b3 ka2b1 displaystyle mathbf a times mathbf b mathbf i a 2 b 3 mathbf j a 3 b 1 mathbf k a 1 b 2 mathbf i a 3 b 2 mathbf j a 1 b 3 mathbf k a 2 b 1 acilimi elde ederiz Laplace acilimi ile en usteki satiri kullanarak a b a2a3b2b3 i a1a3b1b3 j a1a2b1b2 k displaystyle mathbf a times mathbf b begin vmatrix a 2 amp a 3 b 2 amp b 3 end vmatrix mathbf i begin vmatrix a 1 amp a 3 b 1 amp b 3 end vmatrix mathbf j begin vmatrix a 1 amp a 2 b 1 amp b 2 end vmatrix mathbf k yazimini elde ederiz Burada ikili kare dizeylerin tekrar belirtkeni hesaplanmalidir OzellikleriGeometrik anlami Sekil 1 Capraz carpim ile paralelkenarin alaniSekil 2 Uc yoneyden elde edilen prizma Capraz carpimin buyuklugu a ve b yoneylerinin paralelkenara tamamlanarak elde edilen paralelkenarin alanina esittir ve asagidaki sekilde gosterilir Sekil 1 A a b a b sin 8 displaystyle A mathbf a times mathbf b mathbf a mathbf b sin theta Yukaridaki denklemden de gorulecegi uzere buyuklugu yazarken iki yoneyin arasinda kalan acinin sinusu kullanilmistir b yoneyi ile Sekil 1 de gosterilen acinin sinusunun carpimini dusunelim b sin 8 displaystyle mathbf b sin theta Bu carpim b yoneyinin a yoneyine dik olan bilesenini verir Birbirine dik olan iki yoneyin buyukluklerinin carpimi da o yoneyler kullanilarak elde edilen paralelkenarin alanini verir Eger iki yoneyimiz de birbirine dik ise arada kalan aci 90 derece sinus ifadesi 1 e esittir ve iki yoneyin buyukluklerinin carpimi olusan diktortgenin alanina esittir a b ve c yoneylerinden olusturulan pirizmanin oylumu hacmi da bir capraz carpim bir de nokta carpim ile bulunabilir Sekil 2 ve asagidaki sekilde yazilir a b c b c a c a b displaystyle mathbf a cdot mathbf b times mathbf c mathbf b cdot mathbf c times mathbf a mathbf c cdot mathbf a times mathbf b Burada dikkat edilmesi gereken bu uclu carpimin sonucunun eksi olabilecegidir ve oylumun buyuklugu daima arti degere sahip olacagi icin oylum V a b c displaystyle V mathbf a cdot mathbf b times mathbf c seklinde gosterilir Islem ozellikleri Carpraz carpim eksi yerdegistirme ozelligine sahiptir a b b a displaystyle mathbf a times mathbf b mathbf b times mathbf a toplama uzerine dagilma ozelligine sahiptir a b c a b a c displaystyle mathbf a times mathbf b mathbf c mathbf a times mathbf b mathbf a times mathbf c ve bir sayil ile carpilmasi asagidaki gibidir ra b a rb r a b displaystyle r mathbf a times mathbf b mathbf a times r mathbf b r mathbf a times mathbf b Birlesme ozelligine sahip degildir Diger taraftan Jakobi ozdesligi ile uclu capraz carpimda sira degistirme islemi yapilabilir a b c b c a c a b 0 displaystyle mathbf a times mathbf b times mathbf c mathbf b times mathbf c times mathbf a mathbf c times mathbf a times mathbf b mathbf 0 Capraz carpimda sadelestirme islemi yapilmaz a b a c ise a yoneyi sifirdan farkli oldugu durumlarda b c kosulu zorunlu degildir Bazi durumlarda b c olsa bile her durumda olmak zorunda degildir Bunun yerine a b a c oldugu durumda asagidaki islem gerceklestirilebilir 0 a b a c a b c displaystyle begin aligned mathbf 0 amp mathbf a times mathbf b mathbf a times mathbf c amp mathbf a times mathbf b mathbf c end aligned Yukaridaki islemde a veya b c sifirdan farkli ise a ve b c arasindaki aci sifirdir Aci sifir ise de birbirlerine ya paraleldirler ya da antiparaleldirler Uzam geometrik tanimi dusunuldugunde a b capraz carpimi a b islemi sonucu elde edilen yeni yoney etrafinda donderildiginde sonucta herhangi bir degisim olmaz Bu duruma benzer bir durum M displaystyle scriptstyle M dizeyi ile gosterilen donusum dusunuldugunde asagidaki sekilde gosterilebilir Ma Mb detM M T a b displaystyle M mathbf a times M mathbf b det M M T mathbf a times mathbf b yukaridaki yazimda M displaystyle scriptstyle M dizeyi 3 e 3 bir dizeydir ve M T displaystyle scriptstyle M T M displaystyle scriptstyle M dizeyinin terscaprazidir M displaystyle scriptstyle M dizeyi donusume karsilik gelirken M T displaystyle scriptstyle M T dizeyi M displaystyle scriptstyle M dizeyi ile elde edilen donusumun tersine karsilik gelmektedir Yukaridaki denkligi kelimelerle anlatirsak a ve b yoneylerinin ayri ayri M displaystyle scriptstyle M dizeyi ile donusumu alindiktan sonra elde edilen yoneylerin capraz carpimi a b capraz carpimi yapildiktan sonra M T displaystyle scriptstyle M T dizeyi ile yapilan donusum birbirine denktir Burada detM displaystyle det M dizeyin belirtkeninin determinantinin 1 den farkli olmasi durumunda esitligin bozulmamasi icin konulmustur M displaystyle scriptstyle M dizeyinin belirtkeni 1 den farkli ise bir yoneyin M displaystyle scriptstyle M dizeyi ile donusumu yapildiginda yoneyin boyu degismektedir Iki yoneyin capraz carpimi 3 boyutlu uzayda daima iki yoney kullanilarak yazilan sutun seklindeki dizeyin bosuzayindadir Bu durum asagidaki sekilde gosterilir a b NS ab displaystyle mathbf a times mathbf b in NS left begin bmatrix mathbf a mathbf b end bmatrix right Iki capraz carpimin toplami icin asagidaki ozdeslik gecerlidir a b c d a c b d a d c b displaystyle mathbf a times mathbf b mathbf c times mathbf d mathbf a mathbf c times mathbf b mathbf d mathbf a times mathbf d mathbf c times mathbf b Ayrica bakiniz iki kumenin bir carpimi Nokta carpim uc vektorden daha fazla carpim iceriyor sembolu NotlarKaynakcaCajori Florian 1929 A History Of Mathematical Notations Volume II Open Court Publishing s 134 ISBN 978 0 486 67766 8 1948 Chapter 2 Vector Product pp 11 31 London Methuen Publishing Wilson Edwin Bidwell 1901 Vector Analysis A text book for the use of students of mathematics and physics founded upon the lectures of J Willard Gibbs Dis baglantilarHazewinkel Michiel Ed 2001 Cross product Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Eric W Weisstein Cross Product MathWorld A quick geometrical derivation and interpretation of cross products25 Haziran 2010 tarihinde Wayback Machine sitesinde Z K Silagadze 2002 Multi dimensional vector product Journal of Physics A35 4949 5 Eylul 2015 tarihinde Wayback Machine sitesinde it is only possible in 7 D space Real and Complex Products of Complex Numbers 8 Temmuz 2014 tarihinde Wayback Machine sitesinde created at Syracuse University requires W Kahan 2007 Cross Products and Rotations in Euclidean 2 and 3 Space University of California Berkeley PDF 10 Eylul 2014 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State