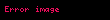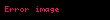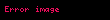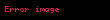Sarsım (ayrıca ekivme), fizikte ivmenin değişme oranı, yani ivmenin zamana göre türevi, hızın zamana göre ikinci türevi ve konumun zamana göre üçüncü türevidir. Sarsım aşağıdaki gibi ifade edilebilir:
Sarsım vektörel bir büyüklüktür ve onun skaler büyüklüğünü ifade etmeye yarayan (örn. vektörel hız ile skaler hız arasında olduğu gibi) ayrıca bir birim yoktur. Vektörel olan bu büyüklük metrik sistemde metre bölü saniye küp (metre bölü saniye bölü saniye bölü saniye, m/s3 ya da m·s−3) olarak tanımlanır. Sarsım için uluslararası kabul edilmiş bir sembol yoktur, ancak İngilizce jerk kelimesinin baş harfi j yaygın olarak kullanılır. Ayrıca ivmenin türevi anlamında ȧ olarak da kullanılabilir.
Ayrıca fizikteki kuvvet kavramının kütle ile ivmenin çarpımı olduğu düşünülürse, kuvvetin türevi gücüm de kütle ile sarsımın çarpımı olarak bulunur (Benzeri bir şekilde momentum da kütle ve hızın çarpımıdır.)
Uygulamaları
Sarsım mühendislikte kullanılmaktadır. Özellikle gibi güvenliğin önemli olduğu uygulamalarda ivmenin de değişikliğini (yani sarsımı) bilmek, güvenlik için önemlidir. Yolcuların stres durumundaki değişiklikler için gereken onun üzerine oturacagindan bir sabit güç hissetmis olacak; whereas pozitif jerk cisim üzerinde artan güç olarak felt olacaktir, vesüre göz önünde bulundurulduğunda, kaslardaki kasılmaların ya da ağrı durumunun uygun hale getirilebilmesi için sadece maksimum ivmenin değil maksimum sarsımın da belirlenmesi gerekir. Özellikle titreşimlerin uyartılarında sarsım dikkate alınır. Sarsımı ölçmek için sarsımölçer (jerkmetre) kullanılır.
Sarsım aynı zamanda İşlemeli üretim alanında da oldukça önemlidir. Kesme aletinin ivmesinde yaşanabilecek ani değişiklikler üründe hatalara yol açabilir. Bu yüzden bugünkü hareket kontrolörleri sarsım sınırlama özelliğini de içerir.
Ayrıca makine mühendisliğinde kam profili hazırlarken tribolojik nedenlerle sarsım, hız ve ivme ile beraber kullanılır.
Üçüncü dereceden hareket profili
Fizikte bir hareketin oluşabilmesi için sabit bir konumdan başka bir konuma doğru yer değiştirme olmalıdır. Aşağıdaki hız zaman grağine göre yer değişiminin evrelerindeki ivme ve sarsımdaki değişiklik şu şekilde sıralanabilir:

Hareket profili 7 bölümden oluşur:
- ivme artar, sarsım en yüksek pozitif değerdedir.
- sabit ivme (sıfır sarsım)
- ivmelenme azalır, istenen en yüksek hıza ulaşılır, sarsım en yüksek negatif değerdedir.
- sabit hız (sıfır ivme, sıfır sarsım)
- ters yönlü ivme artmaya başlar, sarsım en yüksek negatif değerdedir.
- sabit ters yönlü ivme (sıfır sarsım)
- ters yönlü ivme azalmaya başlar, hız sıfıra yaklaşır, sarsım pozitif en yüksek değerdedir.
Eğer ilk ve son durumlar birbirine oldukça yaklaşırsa, maksimum hız ya da ivme ulaşılamayabilir.
Jerk sistemleri
Bir jerk sistemi böyle bir sistemin davranışı bir jerk denklemi ile tanıtılır, bu formun bir denklemi Sprott 2003:
Örnek için, tasarlanmak istenen uygun basit elektronik devre bir jerk denklemi ile ifade ediliyor . Bu jerk devresi olarak biliniyor
Jerk sistemlerinin daha ilginç özelliklerinden biri olasılığıdır. Aslında,belli iyi-bilinen kaotik sistemler, ve gibi geleneksel üç-birinci-dereceden diferansiyel denklemlerin bir sistemi olarak ifade ediliyor,ama bunun tek bir (oldukça karmaşık olmasına rağmen) jerk denkleminin içinde bileştirilmesi gerekir.
Bir jerk denkleminin örneği aşağıdadır:
Burada A ayarlanabilir bir parametredir. Bu denklemin A=3/5 için bir kaotik çözüm var ve jerk devresi aşağıdaki ile uygulanabilir:

Yukaridaki devre icinde tum dirençlerin esdeğeri,except 

Hesap-dışı açıklama
Jerk hesabı terimleri içinde tanımlandığında kavramsallaştırmak zor olabilir,eğer bu terimlerin içinde tanımı biz biraz basitleştirirsek,bir kuvvet (itme ve çekme) bir nesneye uygulanırsa,nesne harekete geçer.Kuvvet uygulandığı sürece nesne hızlanmaya devam eder.Nesne üzerinde çizgi boyunca hiçbir kuvvet olmadığını düşünüyoruz,sonra aniden nesne üzerinde bir kuvvet uygulanıyor. Bu kuvvet uygulamak ne kadar süre için uygulanıyor düşünmüyoruz. Ancak, gerçekte, kuvvet uygulama anında olmaz. Bir değişim her zaman zamanla olur. Jerk zamanla ivme değişimdir. Tipik olarak, bir kuvvet uygulandığında temas süresi,ikinci bir bölünmedir
Bir duvara tam itme,uygulamadan önce bir saniyenin bir kısmını alır.Eğer zorlamaya başladığınızda parmak uçlarınızda hafifçe basınç olacaktır.Baskı jerkin ne kadar süreceğini belirler. Eğer çok yavaş bir duvara itme varsa, aslında artan itmenin ne kadar olduğunu hissedebilirsiniz.Kuvvette olan değişim birkaç saniyenin arasıyla nispeten uzun bir süresi boyunca oluyor, çünkü böyle bir durumda, jerk, çok düşüktür.Bir kuvvet uygulanir ve kaldırılirsa Jerk olur. Ama böyle bir kuvvetin zamanı bir nesnenin üzerinde hareket olusturursa, burada jerk yoktur. (Bu nedenle ivme sabit ise buradaki sabit bir kuvvettir.)
kuvvet Ne kadar hızlı başlıyor onu itme veya çekme belirler yank ve daha sonra jerk. Pek çok uygulamada, bu kuvvet uygulandığında ne kadar hızlı önemli değildir ve bu nedenle biz genellikle hemen güçlerin uygulandığını düşünüyoruz. Jerkin yakin bir örnegi bir otomobil içinde frenin uygulanmasinin oranıdır.
Deneyimli bir sürücü yavaş yavaş artan bir yavaşlamaya (küçük jerk) neden olan fren uygular. Deneyimsiz bir sürücü ya da bir sürücü acil bir yanıtla yavaşlamada hızlı bir artışa (büyük jerk) neden olan ani fren uygular.Jerk hissiyle yolcunun başının ileri jerk nedeni belirgindir.
Denklemler
(yank: birim zamandaki güç)
(jerk: birim zamandaki ivme)
,aşağıda
ile bölünüyor ve yukarıdaki iki ilişkiden:
Jerk yüksekse, kuvvet veya ivme daha yüksektir. Ivme değişikliği süresi kısaldıkça Bir köşede 'kırbaçlanan' bir lunaparktreni yüksek jerk gibidir. Düzgün jerk için, aşağıdaki denklem uygulanabilir:
burada a : son ivme a. : başlangıç ivmesi j : jerk (ivmenin değişimi) v : son hız u : ilk hız s : mesafe/yerdeğiştirme t : alınan zaman
Ayrıca bakınız
- ,elektrodinamik bir kuvvetin genliği jerk ile orantılıdır
- Şok (mekanik)
- Wheeler-Feynman emme teorisi
- İvme
- Eksarsım
- Gücüm
Notlar
Kaynakça
- Sprott JC (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN .
- Sprott JC (1997). "Some simple chaotic jerk functions" (PDF). Am J Phys. 65 (6). ss. 537-43. Bibcode:1997AmJPh..65..537S. doi:10.1119/1.18585. 13 Haziran 2010 tarihinde kaynağından (PDF). Erişim tarihi: 28 Eylül 2009.
- Blair G (2005). (PDF). Race Engine Technology, 010. 15 Mayıs 2008 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 29 Eylül 2009.
Dış bağlantılar
- , description of jerk in the Usenet Physics FAQ23 Haziran 2011 tarihinde Wayback Machine sitesinde ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Sarsim ayrica ekivme fizikte ivmenin degisme orani yani ivmenin zamana gore turevi hizin zamana gore ikinci turevi ve konumun zamana gore ucuncu turevidir Sarsim asagidaki gibi ifade edilebilir j da dt d2v dt2 d3s dt3 displaystyle vec j frac mathrm d vec a mathrm d t frac mathrm d 2 vec v mathrm d t 2 frac mathrm d 3 vec s mathrm d t 3 a displaystyle vec a ivme v displaystyle vec v hiz s displaystyle vec s konum t displaystyle mathit t zamana karsilik gelir Sarsim vektorel bir buyukluktur ve onun skaler buyuklugunu ifade etmeye yarayan orn vektorel hiz ile skaler hiz arasinda oldugu gibi ayrica bir birim yoktur Vektorel olan bu buyukluk metrik sistemde metre bolu saniye kup metre bolu saniye bolu saniye bolu saniye m s3 ya da m s 3 olarak tanimlanir Sarsim icin uluslararasi kabul edilmis bir sembol yoktur ancak Ingilizce jerk kelimesinin bas harfi j yaygin olarak kullanilir Ayrica ivmenin turevi anlaminda ȧ olarak da kullanilabilir Ayrica fizikteki kuvvet kavraminin kutle ile ivmenin carpimi oldugu dusunulurse kuvvetin turevi gucum de kutle ile sarsimin carpimi olarak bulunur Benzeri bir sekilde momentum da kutle ve hizin carpimidir UygulamalariSarsim muhendislikte kullanilmaktadir Ozellikle gibi guvenligin onemli oldugu uygulamalarda ivmenin de degisikligini yani sarsimi bilmek guvenlik icin onemlidir Yolcularin stres durumundaki degisiklikler icin gereken onun uzerine oturacagindan bir sabit guc hissetmis olacak whereas pozitif jerk cisim uzerinde artan guc olarak felt olacaktir vesure goz onunde bulunduruldugunda kaslardaki kasilmalarin ya da agri durumunun uygun hale getirilebilmesi icin sadece maksimum ivmenin degil maksimum sarsimin da belirlenmesi gerekir Ozellikle titresimlerin uyartilarinda sarsim dikkate alinir Sarsimi olcmek icin sarsimolcer jerkmetre kullanilir Sarsim ayni zamanda Islemeli uretim alaninda da oldukca onemlidir Kesme aletinin ivmesinde yasanabilecek ani degisiklikler urunde hatalara yol acabilir Bu yuzden bugunku hareket kontrolorleri sarsim sinirlama ozelligini de icerir Ayrica makine muhendisliginde kam profili hazirlarken tribolojik nedenlerle sarsim hiz ve ivme ile beraber kullanilir Ucuncu dereceden hareket profiliFizikte bir hareketin olusabilmesi icin sabit bir konumdan baska bir konuma dogru yer degistirme olmalidir Asagidaki hiz zaman gragine gore yer degisiminin evrelerindeki ivme ve sarsimdaki degisiklik su sekilde siralanabilir Hareket profili 7 bolumden olusur ivme artar sarsim en yuksek pozitif degerdedir sabit ivme sifir sarsim ivmelenme azalir istenen en yuksek hiza ulasilir sarsim en yuksek negatif degerdedir sabit hiz sifir ivme sifir sarsim ters yonlu ivme artmaya baslar sarsim en yuksek negatif degerdedir sabit ters yonlu ivme sifir sarsim ters yonlu ivme azalmaya baslar hiz sifira yaklasir sarsim pozitif en yuksek degerdedir Eger ilk ve son durumlar birbirine oldukca yaklasirsa maksimum hiz ya da ivme ulasilamayabilir Jerk sistemleri Bir jerk sistemi boyle bir sistemin davranisi bir jerk denklemi ile tanitilir bu formun bir denklemi Sprott 2003 d3xdt3 f d2xdt2 dxdt x displaystyle frac mathrm d 3 x mathrm d t 3 f left frac mathrm d 2 x mathrm d t 2 frac mathrm d x mathrm d t x right Ornek icin tasarlanmak istenen uygun basit elektronik devre bir jerk denklemi ile ifade ediliyor Bu jerk devresi olarak biliniyor Jerk sistemlerinin daha ilginc ozelliklerinden biri olasiligidir Aslinda belli iyi bilinen kaotik sistemler ve gibi geleneksel uc birinci dereceden diferansiyel denklemlerin bir sistemi olarak ifade ediliyor ama bunun tek bir oldukca karmasik olmasina ragmen jerk denkleminin icinde bilestirilmesi gerekir Bir jerk denkleminin ornegi asagidadir d3xdt3 Ad2xdt2 dxdt x 1 0 displaystyle frac mathrm d 3 x mathrm d t 3 A frac mathrm d 2 x mathrm d t 2 frac mathrm d x mathrm d t x 1 0 Burada A ayarlanabilir bir parametredir Bu denklemin A 3 5 icin bir kaotik cozum var ve jerk devresi asagidaki ile uygulanabilir Yukaridaki devre icinde tum direnclerin esdegeri except RA R A 5R 3 displaystyle R A R A 5R 3 disinda ve tum kapasitorlerin es boyuttadir baskin frekans 1 2pRC displaystyle 1 2 pi RC olacak 0 in cikisi x degiskenine karsi olacak 1 in cikisi x in ilk turevine karsi olacak ve 2 nin cikisi ikinci tureve karsi olacak Hesap disi aciklamaJerk hesabi terimleri icinde tanimlandiginda kavramsallastirmak zor olabilir eger bu terimlerin icinde tanimi biz biraz basitlestirirsek bir kuvvet itme ve cekme bir nesneye uygulanirsa nesne harekete gecer Kuvvet uygulandigi surece nesne hizlanmaya devam eder Nesne uzerinde cizgi boyunca hicbir kuvvet olmadigini dusunuyoruz sonra aniden nesne uzerinde bir kuvvet uygulaniyor Bu kuvvet uygulamak ne kadar sure icin uygulaniyor dusunmuyoruz Ancak gercekte kuvvet uygulama aninda olmaz Bir degisim her zaman zamanla olur Jerk zamanla ivme degisimdir Tipik olarak bir kuvvet uygulandiginda temas suresi ikinci bir bolunmedir Bir duvara tam itme uygulamadan once bir saniyenin bir kismini alir Eger zorlamaya basladiginizda parmak uclarinizda hafifce basinc olacaktir Baski jerkin ne kadar surecegini belirler Eger cok yavas bir duvara itme varsa aslinda artan itmenin ne kadar oldugunu hissedebilirsiniz Kuvvette olan degisim birkac saniyenin arasiyla nispeten uzun bir suresi boyunca oluyor cunku boyle bir durumda jerk cok dusuktur Bir kuvvet uygulanir ve kaldirilirsa Jerk olur Ama boyle bir kuvvetin zamani bir nesnenin uzerinde hareket olusturursa burada jerk yoktur Bu nedenle ivme sabit ise buradaki sabit bir kuvvettir kuvvet Ne kadar hizli basliyor onu itme veya cekme belirler yank ve daha sonra jerk Pek cok uygulamada bu kuvvet uygulandiginda ne kadar hizli onemli degildir ve bu nedenle biz genellikle hemen guclerin uygulandigini dusunuyoruz Jerkin yakin bir ornegi bir otomobil icinde frenin uygulanmasinin oranidir Deneyimli bir surucu yavas yavas artan bir yavaslamaya kucuk jerk neden olan fren uygular Deneyimsiz bir surucu ya da bir surucu acil bir yanitla yavaslamada hizli bir artisa buyuk jerk neden olan ani fren uygular Jerk hissiyle yolcunun basinin ileri jerk nedeni belirgindir Denklemler Y DFDt displaystyle Y frac Delta F Delta t yank birim zamandaki guc j DaDt displaystyle j frac Delta a Delta t jerk birim zamandaki ivme j ym displaystyle j frac y m asagida Dt displaystyle Delta t ile bolunuyor ve yukaridaki iki iliskiden DFDt mDaDt y mj displaystyle frac Delta F Delta t m frac Delta a Delta t implies y mj j DFmDt displaystyle j frac Delta F m Delta t Jerk yuksekse kuvvet veya ivme daha yuksektir Ivme degisikligi suresi kisaldikca Bir kosede kirbaclanan bir lunaparktreni yuksek jerk gibidir Duzgun jerk icin asagidaki denklem uygulanabilir a a jt displaystyle a a jt v u a t 12jt2 displaystyle v u a t frac 1 2 jt 2 s ut 12a t2 16jt3 displaystyle s ut frac 1 2 a t 2 frac 1 6 jt 3 burada a son ivme a baslangic ivmesi j jerk ivmenin degisimi v son hiz u ilk hiz s mesafe yerdegistirme t alinan zamanAyrica bakiniz elektrodinamik bir kuvvetin genligi jerk ile orantilidir Sok mekanik Wheeler Feynman emme teorisi Ivme Eksarsim GucumNotlarKaynakcaSprott JC 2003 Chaos and Time Series Analysis Oxford University Press ISBN 0 19 850839 5 Sprott JC 1997 Some simple chaotic jerk functions PDF Am J Phys 65 6 ss 537 43 Bibcode 1997AmJPh 65 537S doi 10 1119 1 18585 13 Haziran 2010 tarihinde kaynagindan PDF Erisim tarihi 28 Eylul 2009 Blair G 2005 PDF Race Engine Technology 010 15 Mayis 2008 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 29 Eylul 2009 Dis baglantilar description of jerk in the Usenet Physics FAQ23 Haziran 2011 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State