Tek anakütle ortalaması için parametrik hipotez sınaması

Tek anakütle ortalaması için parametrik hipotez sınaması veya tek-örneklem için sınama veya μ için sınama, bir rastgele örneklem ortalaması ile bu örneklemin çekilmiş olduğunu düşündüğümüz anakütlenin μ ile belirtilen "anakütle ortalaması" hakkında bir hipotez değeri belirtilmesinin anlamlı olup olmadığını araştırmamızı sağlayan .

Tek anakütle ortalaması testi için temel varsayımlar

• Örnekleme alınan birimler birbirlerinden bağımsız olarak rastgele seçilmiş olmaları
• Anakütle ya normal dağılıma sahip olmalı ya da örneklem hacminin iyice bilinmesi.

Tek anakütle ortalaması hipotez testinin aşamaları

Bir anakütleden kullanarak "n" örneklem büyüklüğü olan bir rastgele örneklem ele geçirilir; istenilen değerler ölçülür ve 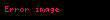${\displaystyle {\bar {x}}}$ (x bar diye okunur) değerindeki örneklem ortalaması bulunur. Hipotez sınaması yönteminde araştırma hedefi bu örneklemin söz konusu anakütleden çekilmiş olup olamayacağını ya da kaynağı olan anakütleden çekilmiş olabilmesinin olasılığının ne olabileceğini ortaya koymaktır.

1. İncelenen araştırma sorusu belirlenmesi;
2. Sıfır hipotez ve oluşturulması;
3. Örnekleme dağılımı ve kritik değer belirlenmesi;
4. Ret alanının belirlenmesi
5. Anlamlılık seviyesi ve şu iki alternatiften biri
   1. Test-istatistiği saptanması;
   2. p-değeri saptanması;
6. Karşılaştırmalar, sonuç ve yorum

Bir pratik örnek problem

Alçı dolum makinemiz μ_o=20 kg ortalama ağırlıklı alçı dolumu yaparken arıza yapar. Tamirci getirip tamir ettiririz. Acaba yine μ_o=20kglık dolum yapabilecek mi?

Deneme yapıp görmek lazım!'

40 torba basit rastgele örnekleme yöntemine göre seçilip bu 40 alçı torbası ağırlıkları şöyle ölçülmüştür:

${\displaystyle X_{1}}$ = 19,8 kg,
${\displaystyle X_{2}}$ = 20,5 kg,
${\displaystyle X_{3}}$ = 21,2 kg,
${\displaystyle X_{4}}$ = 18,9 kg,

.......,

${\displaystyle X_{4}0}$ = 20,8 kg

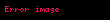
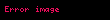
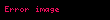
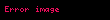
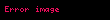
Örneklem istatistikleri şöyle hesaplanmıştır: Örneklem büyüklüğü : n = 40 torba Örneklem ortalaması : 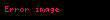${\displaystyle {\bar {x}}}$ = 21,4 kg Örneklem standart sapması: s' = 3,2 kg

Bu problem için yapılan varsayımlar: -Anakütle yani alçı dolum makinesinin yaptığı dolum miktarları normal dağılıma uymaktadır. -Dolum için anakütle standart sapması bilinmemekte ama (yanlılık için ayarlama yapılan) örneklem standart sapması (s') anakütle standart sapması σ için iyi bir kestirimdir.

İncelenen araştırma sorusunun belirlenmesi

Araştırma sorunu tek bir anakütle parametresi, yani anakütle ortalaması ${\displaystyle \mu }$, hakkındadır. Bu anakütle ortalama değeri tam olarak bilinmemekte ve belirlenen bir hipotez değerde ${\displaystyle \mu _{0}}$ (Mü sıfır diye okunur) olduğu varsayılmaktadır. Hipotez testi anakütle ortalamasına verilen değer hakkındadır.

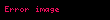
İstenilen araştırma sorusunun tayininde en önemli ilk adım, araştırma sorusunun tayininde, istenilen veya istenmeyen alternatifler ile test edilecek parametrenin belirtilen bir değere eşitsizlik şartına bakılmasıdır. Bu eşitsizlik bir "katı eşitsizlik" midir (yani ≠ veya > veya <) yoksa bir eşitliği de ihtiva eden bir "zayıf eşitsizlik" midir (≤ veya ≥)? Araştırma sorusunun ya katı eşitsizliği ihtiva edip etmediğini mantık yürüterek bulmak gerekmektedir.

Ör./Verilen alçı doldurma makinesi örnek problemi için belirtilen anakutle ortalama değerinin μ=20 olması gerekir. Biraz mantık yürütürsek, hem doldurma ortalamasının 20 kg'den düşük doluş yapmasının hem de doluşun 20 kg'dan daha fazla olması halinin istenmeyen sonuçlar olduğunu kabul edebiliriz. Eğer anakütle ortalaması 20 kg değilse, makine isteğe uygun tamir edilmemiştir; yani araştırma sorusu "katı eşitsizlik" (yani ≠) ihtiva eder.

Sıfır hipotez ve karşıt hipotez oluşturulması

"Sıfır hipotez" (notasyona göre H_o) değerinin oluşturması için hiç problem yoktur. Her türlü parametrik sınamada ve özellikle μ için sınamada, sıfır hipoteze göre μ mutlaka belirtilen parametre değerine (μ_o) eşit olur:

H_o: μ = μ_o

Araştırma sorusu ne olursa olsun mutlaka H_o bu prensibe uyar.

Fakat karşıt hipotez veya alternatif hipotez (notasyona göre H₁) oluşturulması biraz karmaşık olabilir. Karşıt hipotez problemin istediği araştırma sorusu ile ortaya çıkar. Parametrik sınamada karsit hipotezin mutlaka uyduğu bir prensip vardır. Bu prensip

Karşıt hipotez hiçbir zaman eşitlik olamaz.

Karşıt hipotezin ya "eşit değil (≠)" ya "daha düşük değerde (<)" ya da "daha yüksek değerde (>)" olması gerekir. Bunlardan hangisi olacağı önemlidir; çünkü istatistiksel sınamada reddetme bölgesinin nerede olacağı bu karşıt hipotez eşitsizlik şekline dayanır.

Problemin ve araştırma sorusunun tanınması icin ilk yapılacak, istenilen araştırma sorusunun parametrenin belirtilen değere eşit olması şartı ihtiva edip etmediğini tayin etmektir. Araştırma sorusu eşitsizliği ya eşitliği ihtiva eder ya ihtiva etmez ve bu gerçekten ayrı şekillerde karşıt hipotez ortaya çıkar. Bu alternatifleri bir sıraya koyalım ve her alternatifin örnek problemde nasıl ifade edileceğini gösterelim:

1. Eğer araştırma sorusu eşitlik ihtiva etmekteyse: Bu halde probleme çözüm, sıfır hipotezin kabul edilmesi ve karşıt hipotezin ret edilmesi ile verilecektir. Karşıt hipotez istenilen araştırma sorunun aksi işaretli olacaktır. Üç alternatif bulunabilir:

(1.a.) Araştırma sorusunda anakütle ortalamasının belirtilen değere eşit olduğu araştırılmakta ise:
Bu örnek problemde soru "Acaba dolum ortalaması 20kg midir yani μ_o=20kg ?" Bu halde araştırma sorusunun aksi işaretli karşıt hipotez μ_o≠20 kg olur yani hipotezler

H_o=20 H₁≠20

olur.

(1.b.) Araştırma sorusunda anakütle ortalamasının belirtilen değere eşit veya daha küçük olduğu araştırılmakta ise:
Bu örnek problemde soru "Acaba dolum ortalaması, 20kg veya daha aşağı değer de midir yani μ_o≤20kg ?" olur. Aksi işaretli karşıt hipotez bu halde μ_o>20 kg olur; yani hipotezler şunlardır:

H_o=20 H₁>20

(1.c.) Araştırma sorusunda anakütle ortalamasının belirtilen değere eşit veya daha büyük olduğu araştırılmakta ise:
Bu örnek problemde soru "Acaba dolum ortalaması 20kg veya daha yüksek değer de midir yani μ_o≥20kg ?" Bu halde araştırma sorusuna aksi işaretli karşıt hipotez μ_o<20 kg olur yani hipotezler

H_o=20 H₁<20

2. Eğer araştırma sorusu eşitsizlik ihtiva etmekteyse:
Bu halde probleme çözüm sıfır hipotezin ret edilmesi ve karşıt hipotezin kabul edilmesi ile verilecektir. Karşıt hipotez istenilen araştırma sorunun ayni işaretli olacaktır. Üç alternatif bulunabilir:

(2.a.) Anakütle ortalamasının belirtilen değere eşit olmadığı araştırma sorusudur:
Örnek problemde soru "Acaba dolum ortalaması 20kg değil midir yani μ_o≠20kg ?" Bu halde araştırma sorusuna ayni işaretli karşıt hipotez μ_o≠20 kg olur yani hipotezler

H_o=20 H₁≠20

(2.b.) Araştırma sorusu anakütle ortalamasının belirtilen değerden daha küçük olduğu araştırılmakta ise:
Bu örnek problemde soru "Acaba dolum ortalaması 20kgdan daha aşağı değer de midir yani μ_o<20kg ?" Ayni işaretli karşıt hipotez bu halde μ_o<20 kg olur; yani hipotezler

H_o=20 H₁<20

(2.c.) Araştırma sorusu anakütle ortalamasının belirtilen değerden daha büyük olduğu araştırılmakta ise:
Bu örnek problemde soru "Acaba dolum ortalaması 20kgdan daha yüksek değer de midir yani μ_o>20kg ?" Bu halde araştırma sorusuna ayni işaretli karşıt hipotez μ_o>20 kg olur yani hipotezler

H_o=20 H₁>20

Ör./ Verilen pratik problem için belirtilen anakütle ortalama değeri μ=20 olması yani

H_o : μ = 20

Karşıt hipotez için hem ortalama 20 kg'den düşük hem de 20 kg'dan daha fazla dolum istenmeyen sonuçlar olduğu için karşıt hipotez anakütle ortalamasının 20 olmamasıdır; yani

'H₁ : μ ≠ 20 .

Örnekleme dağılımı ve kritik değer belirlenmesi

Hipotez sınaması problemi için değişkenin dağılımı ve örneklem hacminin büyüklüğü, örnekleme dağılımı ve örnekleme dağılımı için kullanılması gereken olasılık dağılımını tespit etmek için kullanılır. Üç alternatif bulunur: 1. Anakütlenin normal dağılım gösterdiği bilinir veya bilindiği kabul edilir. Anakütle normal dağılım gösterirse örneklem hacmi ne olursa olsun (büyük veya küçük fark etmeden) örneklem ortalamasının örnekleme dağılımının normal dağılım olduğu; örnekleme dağılımının örnekleme ortalamasının belirtilen anakütle dağılımına yani;

μ=μ_o

ve standart hatası (yani örneklem ortalamasının örnekleme dağılımının standart sapmasının ya verilen anakütle standart sapmasının veya kestirim anakütle standart sapmasının örneklem hacmi karesine bölünmesi) şu olur;

${\displaystyle \mathrm {SH} ={\frac {\sigma }{\sqrt {n}}}}$

Bu halde örnekleme ortalamasının z-değeri, yani kritik değer, şöyle bulunur:

${\displaystyle z={\frac {{\overline {X}}-\mu }{\mathrm {SH} }}}$

Bu nedenle bu türlü tek anakütle ortalaması sınaması z-testi olarak da adlandırılır.

2. Anakütlenin normal dağılım gösterdiği bilinmez ve bu varsayım olarak da kabul edilmez. Bu halde iki alternatif bulunmaktadır: (2.a.) Basit rastgele örneklem yöntemini göre elde edilmiş n ile ifade edilen büyüktür. Bu büyük örneklem hacmi pratikte örneklem veri sayısının 30'dan büyük olması yani

n > 30

olarak kabul edilir. Bu halde örneklem ortalaması dağılımı için merkezsel limit teoremi uygulanabilir ve örnekleme dağılımı yaklaşık olarak

μ=μ_o örnekleme ortalamalı

ve

${\displaystyle \mathrm {SH} ={\frac {\sigma }{\sqrt {n}}}}$

örneklem standart hatalı bir normal dağılım ile belirlenir. Bu halde örnekleme ortalamasının z-değeri, kritik değer, şöyle bulunur:

${\displaystyle z={\frac {{\overline {X}}-\mu }{\mathrm {SE} }}}$

Bu türlü tek anakütle ortalama sınaması da z-testi olarak adlandırılır.

(2.b.) Basit rastgele örneklem yöntemini göre elde edilmiş küçüktür yani

n ≤ 30

Bu halde 1906'da Student" lakabını taşıyan William Sealy Gosset tarafından bulunan [[Student'in t dağılımı]] uygundur ve bu dağılımın t-testi adıyla küçük örneklem verileri için tek anakütle ortalaması için hipotez sınaması için kullanılması tavisye edilir. Bu halde hipotez testine t-testi adı verilir. Bu halde örnekleme ortalamasının t-değeri, kritik değer, şöyle bulunur:

${\displaystyle t={\frac {{\overline {X}}-\mu }{\mathrm {SH} }}}$

Bu t-dağılımının tam tespiti için ν veya serbestlik derecesi adlı bir parametrenin bulunması da gerekir. Tek anakütle ortalaması için hipotez test için serbestlik derecesi örneklem hacmi eksi bir olur; yani

ν = n - 1

olur.

Ör./ Verilen pratik alçı doldurma makinesi problemi için anakütlenin normal dağılım göstermesi varsayımı uygun görülebilir. Eğer anakütle için normallik varsayımı yapılmasa bile, örneklem hacmi 40 (yani n>30) olarak büyük olduğu kabul edilir. Ayrıca örneklem standart sapmasının anakütle standart sapması için en iyi kestirim olduğu varsayılır. Bu nedenle örnekleme dağılımı standart hatası şöyle hesaplanır:

${\displaystyle \mathrm {SH} ={\frac {\sigma }{\sqrt {n}}}={\frac {3,2}{\sqrt {40}}}=0,506\,\!}$

ve z-değeri veya kritik değer

${\displaystyle z={\frac {{\overline {X}}-\mu }{\mathrm {SH} }}={\frac {21,4-20}{0,506}}=2,767\,\!}$

olur.

Ret alanının belirlenmesi

Ret alanı demek; standart normal dağılım (z-dağılım) veya Student'in t dağılımı (t-dağılımı) eğrisi altında ve ortasında seçtiğimiz (H_o'ın kabul alanı dışında kalan H_o'ın reddedilmesini sağlayan küçük alanlardır. Ret alanı karşıt hipoteze bağlıdır ve üç alternatif şekilde olur:

1. Eğer karşıt hipotez eşitsizlik ise yani

H₁≠ μ_o

o zaman çift yönlüdür yani z-dağılımı veya t-dağılımı eğrilerinin alt-kuyruğu ve üst kuyruğunda bulunur. Eğer biraz ilerideki açıklanacak olan α kullanırsak her iki kuyruk altına kalan alan α/2 olur; iki kuyruktaki ret alanı toplamı α ve ortada bulunan ve kabul alanı 1-α olur.

1. Eğer karşıt hipotez daha büyük ise yani

H₁ > μ_o

ise, o zaman sol-yönlüdür yani z-dağılımı veya t-dağılımı eğrilerinin üst-kuyruğunda bulunur. Bu kuyruk altına kalan alan ve ret alanı α ve ortada sağda bulunan ve kabul alanı 1-α olur.

1. Eğer karşıt hipotez daha küçük ise yani

H₁ < μ_o

ise, o zaman sağ-yönlüdür yani z-dağılımı veya t-dağılımı eğrilerinin alt-kuyruğunda bulunur. Bu kuyruk altına kalan alan ve ret alanı α ve ortada solda bulunan ve kabul alanı 1-α olur.

Ör./Verilen pratik alçı doldurma makinesi problemi için karşıt hipotez 'H₁ : μ ≠ 20 olduğu için ret alanı çift yönlüdür ve hem alt ve hem üst kuyrukta bulunur.

Anlamlılık seviyesi ve isteğe göre test istatistiği veya p-değeri saptanması

Anlamlılık seviyesinin belirlenmesi

Hatasız bir örneklem bulamayacağımız için her testte bir miktar yanılma riskimiz vardır. Bunu 0,05 ; 0,01 ; 0,005 ; 0,0001;... gibi bir seviye olarak benimseyebiliriz. Yanılma payımız küçüldükçe, testin de küçülür. O nedenle olabildiğince az yanılma ile test yapmak isterler. Yine de α =0,05 ve &alfa;=0,01 düzeyleri en çok kullanılanlardır.

Ör./ Alçı doldurma makinesi problemi için α=0,05 seçelim.

Burada tek anakutle ortalaması için hipotez sınaması, her turlu parametrik hipotez sınaması gibi, iki alternatif şekilde devem edilebilir: ya '"test istatistiği" bulunur ya da "p-değeri" bulunur.

İstenirse test istatistiği belirlenmesi

Birinci alternatif, hesapların elle yapılması ve özel standart normal veya Student-t dağılımı tabloları kullanılması için çok uygundur ve eski usulde yapılan analizdir. Bu halde "anlamlılık seviyesi"ne uygun bir z-skor veya t-skoru (yani bu seviyeye tekabül eden normal veya t-eğrileri altındaki alanlar) bulunur. Buna test istatistiği denilir. Buna hedef elde elde edilen kritik değer ile tablodan bulunan test istatistiğini karşılaştırmaktır. Yani bulunacak test istatistiği"

1. İki-yönlü ret alanı için iki sınır değer ± z_α÷2 veya ±t_ν,α÷2  ν=n-1;
2. Sağ-yönlü ret alanı için alt sınır değer: +z_α veya +t_ν,α ν=n-1;
3. Sol-yönlü ret alanı için üst sınır değer: -z_α veya -t_ν,α  ν=n-1

olur. Bunlar için özel standart normal dağılım tablosu veya Student t dağılım tablosu bulunur.

Or./Verilen pratik alçı doldurma makinesi problemi için iki-yönlü ret alanı olduğunu bulmuş, z-dağılımının uygun olduğunu tespit etmiş ve anlamlılık seviyesini 0,05 olduğunu kabul etmiştir; böylece "test istatistiği"

± z_0,05/2 = ±z_0,025

olur. Bir "standart normal dağılım tablosu"na bakarsak, "test istatistiği"nin değerinin ±1.96 olduğu bulunur.

İstenirse p-değeri belirlenmesi

İkinci alternatif, hesapların kompüter kullanılarak yapılması suretiyle ortaya çıkar. Örneğin "Open Office Calc" gibi programları özel olarak NORMAL veya TDIST fonksiyonları için komutaları kullanarak veya "R" özel "istatistik paketi" programlarını kullanarak ters-Z veya ters-t yöntemi ile "p-değeri" bulunur. "P-değeri" kritik değer olan z-değer veya t-değerin, karşıt eğrilerin altında ne kadar alan kapladıklarını yani kritik değer olasılığını (p İngilizce "probabaility" kelimesinden çıkarılmış) bulmaktır. Genel olarak p-değeri hep üst-kuyruk altında kalan alan değerini verir; ama bunun kullanılan "kutuçizim" ve "istatistik paketi" programlarında kontrol edilmesi gerekir çünkü değişik kuyruk değerleri de verildiği görülür. Böylece bu p-olasılığı "anlamlılık seviyesi" olasılığı ile karşılaştırmak hedef alınır.

Karşılaştırma, sonuç ve yorum

Bir hipotez testinde sonuç

1. ya "sıfır hipotezi red etmek" yani "karşıt hipotezi" kabul etmek
2. ya da "sıfır hipotezi kabul etmek" yani "karşıt hipotezi" reddetmek;

olur. Bunun için önceki basamaktaki kullanılan iki alternatife göre şu karşılaştırmadan biri yapılır:

1. ya "kritik değer" ile "test istatistiği" ;
2. ya da "p-değeri" ile "anlamlılık seviyesi" .

Bu karşılaştırmaya göre sonuç ret alanına düşerse "sıfır hipotez" reddedilir:

1. "Kritik değer" ile "test istatistiği" karşılaştırılması halinde:
   1. Eğer ret alanı iki-yönlü ise, "kritik değer" pozitif ve negatif iki "test istatistiği" değerleri dışına düşerse;
   2. Eğer ret alanı sağ-yönlü ise, "kritik değer" pozitif "test istatistiği" değerinden yüksekse;
   3. Eğer ret alanı sol-yönlü ise, "kritik değer" negatif "test istatistiği" değerinden düşükse;
2. "p-değer" ile "anlamlılık seviyesi" karşılaştırılması halinde:
   1. Eğer ret alanı iki-yönlü ise, "p-değeri" - alpha/2; değeri altına ve + alpha/2 üstüne düşerse;
   2. Eğer ret alanı sağ-yönlü ise, "p-değeri değeri" +alpha değerinden altına düşerse;
   3. Eğer ret alanı sol-yönlü ise, "kritik değer" -alpha değerinden üstüne düşerse.

Or/ Örnek alçı doldurma makinesi problemi için şu karşılaştırmalar yapılıp sonuç çıkartılabilir:

1. İki-yönlü ret alanı: Kritik değer=2,767. Test istatistiği=±1,96. Kritik değer pozitif +1.96 dışına düşmekte. "Sıfır hipotez" ret edilmelidir ("Karşıt hipotez" kabul edilmelidir.)
2. İki yönlü ret alanı: p-değeri= ...... + alpha/2=±0,025. p-değeri üst +0.025 seviyesinden daha küçüktür. "Sıfır hipotez" ret edilmelidir ("Karşıt hipotez" kabul edilmelidir.)

Bu duruma göre: elimizdeki örneklemin ortalaması, problem için anakütlenin ortalamasından çok uzağa düşen bir büyüklüktedir ve H_o hipotezini kabul edilemez. Demek ki, bu makine hatalı dolum yapmakta, ortalaması 20 kg olan dolumlar gerçekleştirememektedir.

Hipotez sınaması ve güven aralığı

Genel olarak hipotez sınaması ve güven aralığı değişik matematik ve felsefi önerilere bağlı olarak geliştirilmişlerdir. Bu nedenle bu iki çıkarımsal istatistik yöntemini birbiri ile karıştırmamak ve ikisini ayrı olarak ayrı şekilde kullanmak tavsiye edilmektedir.

Fakat yine de bazı istatistik ders kitapları &alpha anlamlılık seviyesine göre iki-yönlü ret alanı bulunan hipotez sınaması problemi çözmekte iken, aralık kestirimi-güven aralığı kavramları kullanarak (1-&alpha) güven seviyeli bir güven aralığı ortaya çıkarmakta; bu güven aralığının alt ve üst sınırlarını sıfır hipotez olarak belirtilen anakütle ortalaması ile karşılaştırmakta ve eğer sıfır hipotez μ değeri güven aralığı alt ve üst değerleri arasında kalırsa sıfır hipotezi kabul etmekte ve dışında kalırsa sıfır hipotezi reddetmektedirler.

Bu çeşit bir "çözüm" (eğer çözüm denilirse), bir olasılık ölçüsü olan "anlamlılık seviyesi" (&alpha) kavramı ile bir olasılık ölçüsü olmayan ile (ama yine notasyonla 1-%alpha şeklinde olan) çokluluk seviyesi olan "güven seviyesi" kavramını karıştırmaya dayanmaktadır. Bu kavram karışıklığının yapılmaması çok daha uygun bir tutum ve yaklaşım olacağı gayet açıktır.

Dipnotlar

Ayrıca bakınız

• Ortalama
• Anlamlılık seviyesi
• Güven aralığı
• p-değeri
• Standart normal dağılım
• Student'in t dağılımı