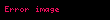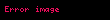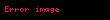Anlamlılık seviyesi, istatistik biliminde, İngiliz istatistikçi Ronald Fisher tarafından yönteminin kurulması sırasında kavramlaştırılmış özel bir manası olan bir bilimsel ve istatistiksel terimdir. İstatistiksel anlamlılık eğer bir sonucun gerçekleşme olasılık değerlendirilmesine göre olabilirliği düşük değil ise ortaya çıkar.

İstatistik teorisine göre açıklamalar
Anlamlılık istatistik biliminde özel bir manası olan ve daha komplike bir istatistik kavramını çok kısa olarak isimlendirilmek için kullanılan özel bir terimdir. Günlük dilde anlamlılık manası olan veya önemi olan lügat manasını taşımaktadır. İstatistiksel anlamlılık bu günlük anlamlılık manasına tam olarak eşit değildir; ve arkasında bir olasılık bulunan bir mana taşımaktadır. Ülkenin belirli bir bölgesinde uygulanan ve binlerce kişilik örneklemlere tatbik edilen bir zeka testinin sayısal sonuçlarını kullanılarak yapılan hesaplamalar sonunda elde edilen ortalama değerlere göre bir bölgenin ortalama zeka testi sonucu ile diğer bir bölgenin ortalama zeka testi sonucu arasında 1/20 bir fark olduğu %5 anlamlılık düzeyli hipotez sınaması ile ortaya çıkmış olsun. Bu çıkartımsal sonuç istatistiksel anlamlı olacaktır; fakat ortalamalar arasındaki 1/20 farkın alelade kullanılan dil anlamı ile pek önemli olmadığı gayet açıktır. Bu nedenle birçok bilimsel araştırmacılar istatiksel hipotez testleri analizde kullanıldığı zaman etki büyüklüğü istatistiğinde verilmesini ve böylelikle farkların pratik öneminin açıkça belirtilmesini çok sıkı olarak tavsiye etmektedirler.
Bir olayın ortaya çıkma şansının olasılığının çok küçük olduğunu kabul etmek için gereken kanıtların miktarı 'anlamlılık düzeyi veya kritik p-değeri olarak isimlendirilir. Geleneksel Fisher-tipi istatistiksel hipotez sınaması teorisi içinde p-değeri gözümlenen veriler veya daha çok dışsal veriler için sıfır hipotezin şartlı olasılığıdır. Eğer hesaplanan p-değeri küçükse, o zaman ya sıfır hipotez yanlıştır veya çok ender ve olağan olmayan bir olay ortaya çıkmıştır. Burada p-değerlerinin herhangi bir örneklem tekrarlanması yorumu olmadığını ve örneklem tekrarı gereğini ifade etmediğini vurgulamak gerekmektedir.
İstatistiksel hipotez sınaması çerçevesini Fisher-tipinden değişik açıklayan diğer bir felsefi temel de bulunmaktadır. Bu "Neyman-Pearson leması" adı altında olasılığın çokluluk temeline dayandıran felsefi açıklamanın bir gelişmesidir. Bu "çokluluk ekolü" açıklamasında, açıkça tanımlanmasını gerekmektedir ve bunun için gerekli örneklem tekrarlanması prosedürünün özellikleri incelenmektedir. Bu yaklaşım, "Hatalı pozitif" veya yani sıfır hipotezin gerçekte kabul edilmesi gerekirken bu hipotezin ret edilmesi olasılığı ile yani sıfır hipotezin yanlış olup gerçekte ret edilmesi gerekirken o hipotezi kabul etme kararı olasılı karşılaştırılmasını önermektedir.
Tipik olarak bir hipotez sınaması "anlamlılık düzeyi", yani kabul edilmesi gerekli bir doğru sıfır hipotezin ret edilmesi, olasılığının önceden seçilmiş bir olasılıktan daha fazla olmaması"dır. Böylece bazı enformasyon kullanılmayıp boşa gitmekle beraber hesaplama külfeti azaltılmakta ve testlerin anlamlılığı olmayan istatistikleri kullanarak gerçekleştirilmesine izin vermektedir.
Fisher tipi p-değerleri, Neyman-Pearson Tıp İ hatalardan felsefi olarak değişiktir. Bu değişikliğin anlaşılmaması bir hata olup ne yazık ki birçok istatistik ders kitabında bu eksiklik devam edip gitmektedir.
Pratikte kullanış
Anlamlılık seviyesi notasyon olarak genellikle Yunan harfi alfa, α, ile belirtilir. Pratikte çok popüler olarak kullanılan anlamlılık seviyesi %5 (0,05), %1 (0,01) ve %0,1 (0.001)'dir.
Eğer bir istatistiksel hipotez sınaması için hesaplamalar α-seviyesinden küçük olan bir p-değeri ortaya çıkarırsa, o zaman "sıfır hipotez" reddedilir. Bu türlü analiz sonuçları, pek teorik olmayan bir yaklaşımla, "istatistiksel olarak anlamsız" olarak nitelendirilir. Örneğin, eğer bir istatistik kullanıcı "bu olayın rastlantı olarak ortaya çıkma şansı binde birdir" diye bir sonuç verirse, bu daha formel olarak 0,001 istatistiksel anlamlılık olarak açıklanabilir. Anlamlılık seviyesi ne kadar düşük olursa, gereken kanıtın o kadar daha güçlü olması gerekmektedir.
İstatistiksel çalışmalarda anlamlılık seviyesinin seçilmesi araştırmacının keyfine bağlıdır ama geleneksel olarak birçok uygulamada seçilen anlamlılık seviyesi %5 olmaktadır ve buna tek neden sırf geleneksel kullanıştır.
Bazı hallerde ise daha istatistiksel anlamlılık seviyesini (1 − α) kabul etmek daha uygun olur. Genellikle bir çalışmada kullanılan anlamlılık seviyesini tefsir etmek için istatistiksel sınamanın yapılma nedeninin iyice anlaşılmasını gerektirir.
Bazı bilim ve teknoloji alanlarında, örneğin nükleer ve parçacık fiziki uygulama alanlarında istatistiksel anlamlılık bir normal dağılım standart sapması olan "σ" (sigma) birimleri ile ifade edilir. Bu şekilde ifade edilen bir istatistiksel anlamlılık değeri olan
alfa α ile ifade edilen anlamlılık seviyesine şu kullanılarak dönüştürülebilir:
Anlamlılık seviyesini σ ile ifade edilmesi bilimciler arasında çok popüler olarak olasılık ve belirsizliğin ölçülmesi için normal dağılımın kullanılmasına açıkça işaret etmektedir.
Bu kullanışa bir örneğine göre, bir teori bir parametrenin değerinin (diyelim) 100 olduğuna işaret etmekte ise ve deneyle ölçülen parametre değeri 109 ± 3 ise, o zaman bu sonucu açıklamak için ölçülmenin teorik tahminden "3σ sapma" ile ortaya çıktığı ifade edilir. Eğer aynı ölçüm α ile ifade edilmek istenirse ifadenin şekli şu olur: "Eğer teori doğru ise, bu deneysel ölçümün rastlantı olarak elde edilmesinin olasılığı
- 1 − erf(3/√2) = 0.0027
yani %0,27 olur.
İstatistiksel çalışmaların sonuçlarını bildirilmesi sırasında %5, %1 veya %0,1 gibi sabit olan anlamlılık seviyelerinin kullandıktan sonra sadece kullanılan anlamlılık seviyesi ve sıfır hipotezin kabul ve reddedildiğini açıklamak yıllardır yeterli bilgi olarak sayılmıştır. Ancak günümüzde bu çeşit açıklamaların yeterli olamadığı ve ancak açıklayıcı veri analizleri için uygun olacağı kabul edilmektedir. Günümüz için bir deneyin veya bir ciddi çalışmanın için kullanıla istatistiksel hipotez testlerinin en son sonuçları hakkında bilgi verilmekte iken hesaplanan p-değerin açıkça belirtilmesi tavsiye edilmektedir. Ayrıca bu p-değeri verildikten sonra bu değerin istatistiksel anlamlılığı olup olmadığı hakkında araştırmacı şahsi hükümü de belirtilmesi istenmektedir. Bu tavsiyenin ortay çıkmasının başlıca nedeninin, meta analizler denilen birçok değişik deney ve çalışmayı birlikte karşılaştırmalı olarak incelemesinin çok popüler olarak kullanılmaya başlanmasıdır; p-değeri ve analizci sonucu açıkça verilirse bunlara doğrudan doğruya ekstra çalışma yapılmadan meta-analize konulması mümkün olur.
Teorik ve pratik tenkitler ve sorunlar
Amerikan bilim araştırmacıları McCloskey ve Ziliak bu istatistiksel analamlılık kavramının bilim alanında çok ciddi hatalara yol açtığını ve bu nedenle kullanılmaması gereğini iddia etmektedirler. Bu kavrama dayanarak bir sonucu "anlamlığı yok" diye açıklamak, bunun "önemsiz" olmadığı anlamına gelmediğinin bilimcilerde bilinmesi gereğine ve bilinmezse hatalı hipotezlerin kabul edilmesine ve doğru hipotezlerin ret edilmesine yol açabileceğine işaret etmektedirler. Bu hatalı yaklaşımların çok olasılığı bulunduğu için bilimsel sosyetenin hipotez sınaması terimlerini kullanmamasının daha uygun olacağını iddia etmektedirler.
Anlamlılık kavramının sinyal-gürültü oranı şeklinde tefsir edilmesi
İstatistiksel anlamlılık verilmiş bir sonuca olan güvenin belirtilmesi olarak da görülebilir. Karşılaştırmalarla ilgilenen bir çalışmada bu kavram karşılaştırılan grupların arasındaki göreli farka, ölçülmelerin miktarına ve ölçülmeyle ilişkili gürültüye bağlıdır. Diğer anlamla, belirli bir sonucun rastgele olmaması (yani bu sonucun sadece şansa bağlı olmaması) sinyal-gürültü oranına ve örneklem hacmine bağlıdır.
Bu matematiksel ifade edilirse, güven Sackett tarafından verilmiş şu formülle açıklanabilir:
Biraz daha açıklığa kavuşturmak için bu formül şu tablo halinde de temsil edilebilir:
Güvenin, gürültü, sinyal ve örneklem hacmine bağlılığı (tablo şeklinde açıklama )
| Parametre | Parametre artması | Parametre azalışı |
|---|---|---|
| Gürültü | Güvenin azalışı | Güvenin artışı |
| Sinyal | Güvenin artışı | Güvenin azalışı |
| Örneklem hacmi | Güvenin artışı | Güvenin azalışı |
Bu sözcüklerle ifade edilirse, eğer gürültü düşükse ve/veya örneklem hacmi yüksekse ve/veya sinyala efekt hacmi büyükse, güvene bağımlılık yüksektir. Bir sonuç olarak güven (ve ona bağlı olan güven aralığı) sadece efekt hacmine "bağımlı değildir". Eğer örneklem hacmi yüksekse ve gürültü düşük ise, küçük bir efekt hacmi büyük güvenle ölçülebilir. Küçük bir efekt hacminin önemli olup olmadığı karşılaştırması yapılan olaylara bağlıdır.
Tıp bilimi alanında (rizikodaki küçük artışlarda yansıyan) küçük efekt hacmi çok kere kliniksel olarak ilgili görülmektedir ve çok kere (eğer büyük güven varsa) sağlanım kararlarına bir yol gösterici olarak kullanılırlar. Belirli bir sağlanımın değerli uğraşa olarak kabul edilip edilmeyeceği rizikolara, yararlarına ve maliyetlere bağlıdır.
Dipnotlar
- ^ "Bu türde kritik testler "anlamlılık testleri" olarak isimlendirilebilir. Bu türlü testlerin yapılması mümkün ise elde ettiğimiz ilk örneklem verilerinin, ikinci bir örneklem verilerinden anlamlı bir şekilde farklı olup olmadığını ortaya çıkartabiliriz. — Fisher, R.A. (1925). Statistical Methods for Research Workers, Edinburgh: Oliver and Boyd, say.43. (İngilizce)
- ^ Hubbard, Raymond ve Bayarri,M.J. P Values are not Error Probabılıties (P-değerleri hata olasılıkları değildir) 4 Eylül 2013 tarihinde Wayback Machine sitesinde .. Fisher işbat p-değeri ile Neyman-Pearson I. Tip hata seviyesi
arasındaki farkları açıklama hedefli makale. (İngilizce) (Erişme:6.5.2010)
- ^ Stigler, S. (2008), "Fisher and the 5% level", Chance Cilt 21 no.4 say12
- ^ Ziliak, Stephen ve McCloskey, Deirdre, (2008). The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives[]. Ann Arbor, , 2009. (İngilizce) (Erişme:6.5.2010)
- ^ Sackett, D.L. (2001), "Why randomized controlled trials fail büt needn't: 2. Failüre to employ physiological statistics, or the only formula a clinician-trialist iş ever likely to need (or understand!)", CMAJ Cilt:165 No:9 Ekim, say.1226–37 {{|pmid=11706914 |pmc=81587 |doi= |url=http://www.cmaj.ca/cgı/pmıdlookup?view=long&pmid=11706914}} (İngilizce)
Ayrıca bakınız
- İstatistiksel hipotez sınaması
- İstatistiksel bağımsızlık ile klasik anlamlılık hipotez sınaması kavramlarını birleştiren ""
Dış bağlantılar
- İngilizce Wikipedia "Statistical significance" maddesi:[1] 16 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:6.5.2010)
- Thompson, Bruce, (2004). "The 'significance' crisis in psychology and education." Journal of Soçio-Economics, Cilt 33, say. 607-613. (İngilizce) (Erişme:6.5.2010)
- İstatistikte 'anlamlılık' teriminin kullanılması tarihçesi. 3 Kasım 2017 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişme:6.5.2010)
- İstatistiksel anlamlılık sınaması kavramının, sınav değerlendirmeleri konusu odaklı olarak açıklaması 2 Ekim 2010 tarihinde Wayback Machine sitesinde . (İngilizce) (Erişme:6.5.2010)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Anlamlilik seviyesi istatistik biliminde Ingiliz istatistikci Ronald Fisher tarafindan yonteminin kurulmasi sirasinda kavramlastirilmis ozel bir manasi olan bir bilimsel ve istatistiksel terimdir Istatistiksel anlamlilik eger bir sonucun gerceklesme olasilik degerlendirilmesine gore olabilirligi dusuk degil ise ortaya cikar Ortalamadan 1 96 ile 1 96 standart sapma uzaklikta standart normal dagilim golgeleme alaniIstatistik teorisine gore aciklamalarAnlamlilik istatistik biliminde ozel bir manasi olan ve daha komplike bir istatistik kavramini cok kisa olarak isimlendirilmek icin kullanilan ozel bir terimdir Gunluk dilde anlamlilik manasi olan veya onemi olan lugat manasini tasimaktadir Istatistiksel anlamlilik bu gunluk anlamlilik manasina tam olarak esit degildir ve arkasinda bir olasilik bulunan bir mana tasimaktadir Ulkenin belirli bir bolgesinde uygulanan ve binlerce kisilik orneklemlere tatbik edilen bir zeka testinin sayisal sonuclarini kullanilarak yapilan hesaplamalar sonunda elde edilen ortalama degerlere gore bir bolgenin ortalama zeka testi sonucu ile diger bir bolgenin ortalama zeka testi sonucu arasinda 1 20 bir fark oldugu 5 anlamlilik duzeyli hipotez sinamasi ile ortaya cikmis olsun Bu cikartimsal sonuc istatistiksel anlamli olacaktir fakat ortalamalar arasindaki 1 20 farkin alelade kullanilan dil anlami ile pek onemli olmadigi gayet aciktir Bu nedenle bircok bilimsel arastirmacilar istatiksel hipotez testleri analizde kullanildigi zaman etki buyuklugu istatistiginde verilmesini ve boylelikle farklarin pratik oneminin acikca belirtilmesini cok siki olarak tavsiye etmektedirler Bir olayin ortaya cikma sansinin olasiliginin cok kucuk oldugunu kabul etmek icin gereken kanitlarin miktari anlamlilik duzeyi veya kritik p degeri olarak isimlendirilir Geleneksel Fisher tipi istatistiksel hipotez sinamasi teorisi icinde p degeri gozumlenen veriler veya daha cok dissal veriler icin sifir hipotezin sartli olasiligidir Eger hesaplanan p degeri kucukse o zaman ya sifir hipotez yanlistir veya cok ender ve olagan olmayan bir olay ortaya cikmistir Burada p degerlerinin herhangi bir orneklem tekrarlanmasi yorumu olmadigini ve orneklem tekrari geregini ifade etmedigini vurgulamak gerekmektedir Istatistiksel hipotez sinamasi cercevesini Fisher tipinden degisik aciklayan diger bir felsefi temel de bulunmaktadir Bu Neyman Pearson lemasi adi altinda olasiligin cokluluk temeline dayandiran felsefi aciklamanin bir gelismesidir Bu cokluluk ekolu aciklamasinda acikca tanimlanmasini gerekmektedir ve bunun icin gerekli orneklem tekrarlanmasi prosedurunun ozellikleri incelenmektedir Bu yaklasim Hatali pozitif veya yani sifir hipotezin gercekte kabul edilmesi gerekirken bu hipotezin ret edilmesi olasiligi ile yani sifir hipotezin yanlis olup gercekte ret edilmesi gerekirken o hipotezi kabul etme karari olasili karsilastirilmasini onermektedir Tipik olarak bir hipotez sinamasi anlamlilik duzeyi yani kabul edilmesi gerekli bir dogru sifir hipotezin ret edilmesi olasiliginin onceden secilmis bir olasiliktan daha fazla olmamasi dir Boylece bazi enformasyon kullanilmayip bosa gitmekle beraber hesaplama kulfeti azaltilmakta ve testlerinanlamliligiolmayan istatistikleri kullanarak gerceklestirilmesine izin vermektedir Fisher tipi p degerleri Neyman Pearson Tip I hatalardan felsefi olarak degisiktir Bu degisikligin anlasilmamasi bir hata olup ne yazik ki bircok istatistik ders kitabinda bu eksiklik devam edip gitmektedir Pratikte kullanisAnlamlilik seviyesi notasyon olarak genellikle Yunan harfi alfa a ile belirtilir Pratikte cok populer olarak kullanilan anlamlilik seviyesi 5 0 05 1 0 01 ve 0 1 0 001 dir Eger bir istatistiksel hipotez sinamasi icin hesaplamalar a seviyesinden kucuk olan bir p degeri ortaya cikarirsa o zaman sifir hipotez reddedilir Bu turlu analiz sonuclari pek teorik olmayan bir yaklasimla istatistiksel olarak anlamsiz olarak nitelendirilir Ornegin eger bir istatistik kullanici bu olayin rastlanti olarak ortaya cikma sansi binde birdir diye bir sonuc verirse bu daha formel olarak 0 001 istatistiksel anlamlilik olarak aciklanabilir Anlamlilik seviyesi ne kadar dusuk olursa gereken kanitin o kadar daha guclu olmasi gerekmektedir Istatistiksel calismalarda anlamlilik seviyesinin secilmesi arastirmacinin keyfine baglidir ama geleneksel olarak bircok uygulamada secilen anlamlilik seviyesi 5 olmaktadir ve buna tek neden sirf geleneksel kullanistir Bazi hallerde ise daha istatistiksel anlamlilik seviyesini 1 a kabul etmek daha uygun olur Genellikle bir calismada kullanilan anlamlilik seviyesini tefsir etmek icin istatistiksel sinamanin yapilma nedeninin iyice anlasilmasini gerektirir Bazi bilim ve teknoloji alanlarinda ornegin nukleer ve parcacik fiziki uygulama alanlarinda istatistiksel anlamlilik bir normal dagilim standart sapmasi olan s sigma birimleri ile ifade edilir Bu sekilde ifade edilen bir istatistiksel anlamlilik degeri olan ns displaystyle n sigma alfa a ile ifade edilen anlamlilik seviyesine su kullanilarak donusturulebilir a 1 erf n 2 displaystyle alpha 1 operatorname erf left n sqrt 2 right Anlamlilik seviyesini s ile ifade edilmesi bilimciler arasinda cok populer olarak olasilik ve belirsizligin olculmesi icin normal dagilimin kullanilmasina acikca isaret etmektedir Bu kullanisa bir ornegine gore bir teori bir parametrenin degerinin diyelim 100 olduguna isaret etmekte ise ve deneyle olculen parametre degeri 109 3 ise o zaman bu sonucu aciklamak icin olculmenin teorik tahminden 3s sapma ile ortaya ciktigi ifade edilir Eger ayni olcum a ile ifade edilmek istenirse ifadenin sekli su olur Eger teori dogru ise bu deneysel olcumun rastlanti olarak elde edilmesinin olasiligi 1 erf 3 2 0 0027 yani 0 27 olur Istatistiksel calismalarin sonuclarini bildirilmesi sirasinda 5 1 veya 0 1 gibi sabit olan anlamlilik seviyelerinin kullandiktan sonra sadece kullanilan anlamlilik seviyesi ve sifir hipotezin kabul ve reddedildigini aciklamak yillardir yeterli bilgi olarak sayilmistir Ancak gunumuzde bu cesit aciklamalarin yeterli olamadigi ve ancak aciklayici veri analizleri icin uygun olacagi kabul edilmektedir Gunumuz icin bir deneyin veya bir ciddi calismanin icin kullanila istatistiksel hipotez testlerinin en son sonuclari hakkinda bilgi verilmekte iken hesaplanan p degerin acikca belirtilmesi tavsiye edilmektedir Ayrica bu p degeri verildikten sonra bu degerin istatistiksel anlamliligi olup olmadigi hakkinda arastirmaci sahsi hukumu de belirtilmesi istenmektedir Bu tavsiyenin ortay cikmasinin baslica nedeninin meta analizler denilen bircok degisik deney ve calismayi birlikte karsilastirmali olarak incelemesinin cok populer olarak kullanilmaya baslanmasidir p degeri ve analizci sonucu acikca verilirse bunlara dogrudan dogruya ekstra calisma yapilmadan meta analize konulmasi mumkun olur Teorik ve pratik tenkitler ve sorunlarAmerikan bilim arastirmacilari McCloskey ve Ziliak bu istatistiksel analamlilik kavraminin bilim alaninda cok ciddi hatalara yol actigini ve bu nedenle kullanilmamasi geregini iddia etmektedirler Bu kavrama dayanarak bir sonucu anlamligi yok diye aciklamak bunun onemsiz olmadigi anlamina gelmediginin bilimcilerde bilinmesi geregine ve bilinmezse hatali hipotezlerin kabul edilmesine ve dogru hipotezlerin ret edilmesine yol acabilecegine isaret etmektedirler Bu hatali yaklasimlarin cok olasiligi bulundugu icin bilimsel sosyetenin hipotez sinamasi terimlerini kullanmamasinin daha uygun olacagini iddia etmektedirler Anlamlilik kavraminin sinyal gurultu orani seklinde tefsir edilmesiIstatistiksel anlamlilik verilmis bir sonuca olan guvenin belirtilmesi olarak da gorulebilir Karsilastirmalarla ilgilenen bir calismada bu kavram karsilastirilan gruplarin arasindaki goreli farka olculmelerin miktarina ve olculmeyle iliskili gurultuye baglidir Diger anlamla belirli bir sonucun rastgele olmamasi yani bu sonucun sadece sansa bagli olmamasi sinyal gurultu oranina ve orneklem hacmine baglidir Bu matematiksel ifade edilirse guven Sackett tarafindan verilmis su formulle aciklanabilir guven sinyalgurultu orneklem hacmi displaystyle mathrm guven frac mathrm sinyal mathrm gurultu times sqrt mathrm orneklem hacmi Biraz daha acikliga kavusturmak icin bu formul su tablo halinde de temsil edilebilir Guvenin gurultu sinyal ve orneklem hacmine bagliligi tablo seklinde aciklama Parametre Parametre artmasi Parametre azalisiGurultu Guvenin azalisi Guvenin artisiSinyal Guvenin artisi Guvenin azalisiOrneklem hacmi Guvenin artisi Guvenin azalisi Bu sozcuklerle ifade edilirse eger gurultu dusukse ve veya orneklem hacmi yuksekse ve veya sinyala efekt hacmi buyukse guvene bagimlilik yuksektir Bir sonuc olarak guven ve ona bagli olan guven araligi sadece efekt hacmine bagimli degildir Eger orneklem hacmi yuksekse ve gurultu dusuk ise kucuk bir efekt hacmi buyuk guvenle olculebilir Kucuk bir efekt hacminin onemli olup olmadigi karsilastirmasi yapilan olaylara baglidir Tip bilimi alaninda rizikodaki kucuk artislarda yansiyan kucuk efekt hacmi cok kere kliniksel olarak ilgili gorulmektedir ve cok kere eger buyuk guven varsa saglanim kararlarina bir yol gosterici olarak kullanilirlar Belirli bir saglanimin degerli ugrasa olarak kabul edilip edilmeyecegi rizikolara yararlarina ve maliyetlere baglidir Dipnotlar Bu turde kritik testler anlamlilik testleri olarak isimlendirilebilir Bu turlu testlerin yapilmasi mumkun ise elde ettigimiz ilk orneklem verilerinin ikinci bir orneklem verilerinden anlamli bir sekilde farkli olup olmadigini ortaya cikartabiliriz Fisher R A 1925 Statistical Methods for Research Workers Edinburgh Oliver and Boyd say 43 Ingilizce Hubbard Raymond ve Bayarri M J P Values are not Error Probabilities P degerleri hata olasiliklari degildir 4 Eylul 2013 tarihinde Wayback Machine sitesinde Fisher isbat p degeri ile Neyman Pearson I Tip hata seviyesi a displaystyle alpha arasindaki farklari aciklama hedefli makale Ingilizce Erisme 6 5 2010 Stigler S 2008 Fisher and the 5 level Chance Cilt 21 no 4 say12 Ziliak Stephen ve McCloskey Deirdre 2008 The Cult of Statistical Significance How the Standard Error Costs Us Jobs Justice and Lives olu kirik baglanti Ann Arbor 2009 Ingilizce Erisme 6 5 2010 Sackett D L 2001 Why randomized controlled trials fail but needn t 2 Failure to employ physiological statistics or the only formula a clinician trialist is ever likely to need or understand CMAJ Cilt 165 No 9 Ekim say 1226 37 pmid 11706914 pmc 81587 doi url http www cmaj ca cgi pmidlookup view long amp pmid 11706914 Ingilizce Ayrica bakinizIstatistiksel hipotez sinamasi Istatistiksel bagimsizlik ile klasik anlamlilik hipotez sinamasi kavramlarini birlestiren Dis baglantilarIngilizce Wikipedia Statistical significance maddesi 1 16 Subat 2010 tarihinde Wayback Machine sitesinde arsivlendi Ingilizce Erisme 6 5 2010 Thompson Bruce 2004 The significance crisis in psychology and education Journal of Socio Economics Cilt 33 say 607 613 Ingilizce Erisme 6 5 2010 Istatistikte anlamlilik teriminin kullanilmasi tarihcesi 3 Kasim 2017 tarihinde Wayback Machine sitesinde Ingilizce Erisme 6 5 2010 Istatistiksel anlamlilik sinamasi kavraminin sinav degerlendirmeleri konusu odakli olarak aciklamasi 2 Ekim 2010 tarihinde Wayback Machine sitesinde Ingilizce Erisme 6 5 2010
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans