Trigonometrik fonksiyonlar, matematikte bir açının işlevi olarak geçen fonksiyonlardır. Geometride üçgenleri incelerken ve periyodik olarak tekrarlanan olayları incelerken sıklıkla kullanılırlar. Genel olarak bir açısı belirli dik üçgenlerde herhangi iki kenarın oranı olarak belirtilirler, ancak birim çemberdeki belirli doğru parçalarının uzunlukları olarak da tanımlanabilirler. Daha çağdaş tanımlarda sonsuz seriler veya belirli bir çözümü olarak geçerler.



Temel fonksiyonlar
Çağdaş kullanımda, aşağıdaki tabloda da gösterildiği üzere altı tane temel trigonometrik fonksiyon vardır. Özellikle son dördünde, bu bağıntılar bu fonksiyonların tanımları olarak geçer, ama bu fonksiyonlar geometrik veya başka yollardan da tanımlanabilirler ve bu bağıntılar o yollardan da çıkarılabilir. Bu fonksiyonlar arasındaki birçok bağıntı sayfasında görülebilir.

| Fonksiyon | Kısaltma | İlişki |
| Sinüs | sin | 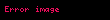 |
| Kosinüs | cos | 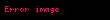 |
| Tanjant | tan | 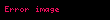 |
| Kotanjant | cot | 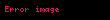 |
| Sekant | sec |  |
| Kosekant | csc (veya cosec) |  |
Sinüs ve Kosinüs fonksiyonları
1. f(x) = sin(x) işlevi dik üçgen'de karşı dik kenarın hipotenüse oranıdır. Koordinat Düzleminde "y" ekseni olarak tabir edilir. Bu işlevin tanım aralığı [-1,1] dir. Yani, sinüs fonksiyonunun değeri -1'den küçük 1'den büyük olamaz.
2. f(x) = cos(x) işlevi dik üçgende Komşu dik kenarın hipotenüse oranıdır. Koordinat düzleminde "x" ekseni olarak tabir edilir. Tanım aralığı f(x) = sinx işleviyle aynıdır.
Sinüs ve Kosinüs işlevleri arasında Pisagor teoreminden çıkarılabilen; 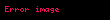
Tanjant ve Kotanjant işlevleri
3. f(x) = tanx işlevi dik üçgende Karşı dik kenarın komşu dik kenara oranıdır. Koordinat düzleminde Birim çembere "x" ekseninin pozitif tarafında teğet ve x eksenine diktir. Tanım aralığı (-∞,+∞) dır. Ayrıca 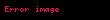
4. f(x) = cotx işlevi dik üçgende Komşu dik kenarın karşı dik kenara oranıdır. Koordinat düzleminde Birim çembere "y" ekseninin pozitif yönünde teğet ve y eksenine diktir. Tanım aralığı (-∞,+∞) dır.
Tanjant ve Kotanjant işlevleri arasında birim çemberde benzerlik yapılarak veya Pisagor teoreminden bulunabilen 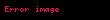
Trigonometrik fonksiyonların özel değerleri
Aşağıdaki tabloda gösterildiği gibi Trigonometrik fonksiyonların bazı yaygın olarak kullanılan özel değerleri vardır,
| Fonksiyon | 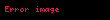 | 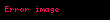 | 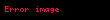 | 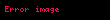 | 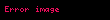 | 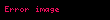 | 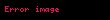 |
|---|---|---|---|---|---|---|---|
| sin |  | 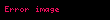 | 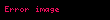 | 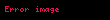 | 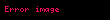 |  |  |
| cos |  |  | 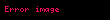 | 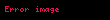 | 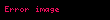 | 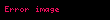 |  |
| tan |  | 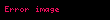 | 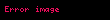 |  |  | 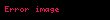 | Tanımsız |
| cot | Tanımsız | 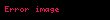 |  |  | 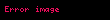 | 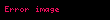 |  |
| sec |  | 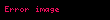 | 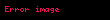 |  | 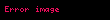 |  | Tanımsız |
| csc | Tanımsız |  | 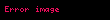 |  | 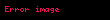 | 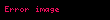 |  |
Diğer trigonometrik fonksiyonlar
Yukarıda ifade edilenlerle birlikte, daha önce hiç duymamış olabileceğiniz ek trigonometrik fonksiyon aileleri vardır. Bunlar şunları içerir: Versine, Vercosine, Coversine, Covercosine, Exsecant, Excosecant, Haversine, Havercosine, Hacoversine, Hacovercosine.
Bunlar, temel üç trigonometrik fonksiyonun temel kombinasyonları için basit isimler olup özdeşlikleri aşağıdaki tabloda verilmiştir:
| Fonksiyon | Kısaltma | Özdeşlik |
| Versinüs | versin(θ) | 1 – cos(θ) |
| Verkosinüs | vercosin(θ) | 1 + cos(θ) |
| Koversinüs | coversin(θ) | 1 – sin(θ) |
| Koverkosinüs | covercosin(θ) | 1 + sin(θ) |
| Ekssekant | exsec(θ) | sec(θ) – 1 |
| Ekskosekant | excsc(θ) | csc(θ) – 1 |
| Haversinüs | haversin(θ) | versin(θ)/2 |
| Haverkosinüs | havercosin(θ) | vercosin(θ)/2 |
| Hakoversinüs | hacoversin(θ) | coversin(θ)/2 |
| Hakoverkosinüs | hacovercosin(θ) | covercosin(θ)/2 |
Birim çemberde tanımlar

Bu altı trigonometrik fonksiyon birim çember'de tanımlanabilir, yarıçapı bir birim olan çemberdir. Birim çember tanımı pratik hesaplamada çok yararlar sağlar; aslında çoğu açıları için dik üçgeni kullanabiliriz. Açılar 0 ve π/2 radyan'la sınırlı değildir. Birim çember bütün pozitif ve negatif açıların trigonometrik değerlerini tanımlar
Ayrıca tek bir görsel resim Aynı anda tüm önemli üçgenlerin içinde saklanmasını sağlar. Pisagor teoremi'nden yararlanılarak birim çemberde şu denklemi kurabiliriz:
Bu resim bazı yaygın açıları, negatif ve pozitif yöndeki ölçüleri, radyan ölçülerini içerir, x-ekseninin pozitif yarısının orijinden çizilen doğru ile yaptığı açı θ’dır, bu birim çemberle kesişir. x- ve y-koordinatlarının bu kesim noktası ile kesiştiği nokta sırasıyla cos θ ve sin θ, değerlerine eşittir. Hipotenüs burada 1'e eşittir. böylece sin θ = y/1 ve cos θ = x/1 olacaktır
Bu değerlerin, kolay biçimde hafızaya alındığını aklınızda bulundurunuz
15°, 18º, 36º, 54°, 72º ve 75° için elde edilen değerleri aşağıdadır.
3º, 6º, 9º, 81º, 84º ve 87º için değerleri analitik olarak hesaplanabilir.

2π ve daha büyük açılar için az-2π ve daha küçük açılar için çember etrafında sadece bir daire etrafında dönmeye devam ederler
- sin ve cos periyodik fonksiyon ve periodu 2π'dir
herhangi bir açı θ ve herhangi bir tam sayı k 'dır.
Seri tanımları

Trigonometrik fonksiyonların Taylor serisi'ne açılımları aşağıdaki gibidir. bütün x:gerçek sayılar için
Bu iki serinin şu toplamı Euler formülü'nü verir: cos x + i sin x = eix. Diğer serilerde bulunabilir. Aşağıdaki trigonometrik fonksiyonlar için:
- Unninci 'dır,
- Bnninci Bernoulli sayısı'dır, ve
- En (aşağıda) ninci Euler sayısı'dır.
Tanjant
Eğer seri tanjant fonksiyonu ilgili faktöriyelleri ile ifade edilecekse, kombinatorik yorumlamada, kardinal tek sayıların sonlu sayıda permütasyon alternatifleri vardır bunlar "tanjant sayıları" olarak adlandırılır.
Kosekant
Secant
Eğer seri sekant fonksiyonu ilgili faktöriyelleri ile ifade edilecekse, kombinatorik yorumlamada, kardinal tek sayıların sonlu sayıda permütasyon alternatifleri vardır bunlar "sekant sayıları" olarak adlandırılır.
Kotanjant
kotanjant fonksiyonu ve ters fonksiyonlar için:
Bu eşitlik hilesi ile ispat edilir.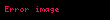

Üstel fonksiyonlar ve karmaşık sayılarla ilişkisi

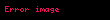 ve
ve 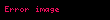 (
( yerine
yerine 
 ).
).Bu eşitlik Euler formülüdür. Karmaşık analizin geometrik yorumlanmasının esasını oluşturur. Örnek olarak Karmaşık düzlem'de birim çemberin e ix, parametrizasyonu gibi. Buradaki paramatreler cos ve sin'dir. Euler formülü ile aşağıdaki sin ve cos yazılabilir:
Dahası, trigonometrik fonksiyonların bu karmaşık argümanları için z tanımını sağlar:
burada i 2 = −1. sin ve cos tam fonksiyon'dur. Ayrıca, x saf gerçeldir,
Ayrıca argümanları gerçek ve sanal kısımları bakımından karmaşık sinüs ve kosinüs fonksiyonları ifade etmek bazen yararlıdır.
Bu (sin, cos) fonksiyonlarından yararlanılarak hiperbolik gerçek (sinh, cosh) karşılıkları bulunabilir.
Karmaşık grafik
Aralık değerinin parlaklığın büyüklüğü (mutlak değeri) gösterir. Parlaklığı siyah olan değer sıfırdır. Renk tonu pozitif reel eksenle ölçülen, argüman veya açı ile değişir.

Ayrıca bakınız
- Trigonometrinin ana hatları
- Hiperbolik fonksiyon
- Birim vektör (cos yön açıklaması)
- Euler formülü
- -köşe açıları bir genellemesi
- -tanjant fonksiyonu tanımı için bir
Notlar
- ^ a b c d Abramowitz, Milton and Irene A. Stegun, p.74
- ^ See Ahlfors, pages 43–44.
- ^ Abramowitz; Weisstein.
- ^ a b Stanley, Enumerative Combinatorics, Vol I., page 149
- ^ ; (2000). Proofs from THE BOOK. Second. Springer-Verlag. s. 149. ISBN . 20 Şubat 2012 tarihinde kaynağından . Erişim tarihi: 27 Haziran 2012.
- ^ Remmert, Reinhold (1991). Theory of complex functions. Springer. s. 327. ISBN . 18 Ocak 2012 tarihinde kaynağından . Erişim tarihi: 27 Haziran 2012., Extract of page 327 7 Haziran 2013 tarihinde Wayback Machine sitesinde .
Kaynakça
- Abramowitz, Milton and Irene A. Stegun, , Dover, New York. (1964). .
- Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, , New York, 1966.
- Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). .
- Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transaction on Mathematical Software (1991).
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). .
- Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli, , Princeton Univ. Press. (1998). Reprint edition (February 25, 2002): .
- Needham, Tristan, " to Visual Complex Analysis2 Haziran 2004 tarihinde Wayback Machine sitesinde .. Oxford University Press, (1999). .
- O'Connor, J.J., and E.F. Robertson, , MacTutor History of Mathematics archive. (1996).
- O'Connor, J.J., and E.F. Robertson, "Madhava of Sangamagramma"26 Şubat 2006 tarihinde Wayback Machine sitesinde ., MacTutor History of Mathematics archive. (2000).
- Pearce, Ian G., "Madhava of Sangamagramma"5 Mayıs 2006 tarihinde Wayback Machine sitesinde ., MacTutor History of Mathematics archive. (2002).
- Weisstein, Eric W., "Tangent"19 Temmuz 2006 tarihinde Wayback Machine sitesinde . from MathWorld, accessed 21 January 2006.
Dış bağlantılar

- Visionlearning Module on Wave Mathematics18 Mart 2008 tarihinde Wayback Machine sitesinde .
- : Visualization of the unit circle, trigonometric and hyperbolic functions
- Dave's draggable diagram.15 Haziran 2008 tarihinde Wayback Machine sitesinde . (Requires java browser plugin)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Trigonometrik fonksiyonlar matematikte bir acinin islevi olarak gecen fonksiyonlardir Geometride ucgenleri incelerken ve periyodik olarak tekrarlanan olaylari incelerken siklikla kullanilirlar Genel olarak bir acisi belirli dik ucgenlerde herhangi iki kenarin orani olarak belirtilirler ancak birim cemberdeki belirli dogru parcalarinin uzunluklari olarak da tanimlanabilirler Daha cagdas tanimlarda sonsuz seriler veya belirli bir cozumu olarak gecerler Trigonometrik islevlerin birim cember uzerinde gosterilmesiTrigonometrik fonksiyonlar Sinus Kosinus Tanjant Kotanjant Sekant Kosekantf x sin x displaystyle f x sin x ve f x cos x displaystyle f x cos x islevlerinin kartezyen uzayinda grafiksel gosterimiTemel fonksiyonlarCagdas kullanimda asagidaki tabloda da gosterildigi uzere alti tane temel trigonometrik fonksiyon vardir Ozellikle son dordunde bu bagintilar bu fonksiyonlarin tanimlari olarak gecer ama bu fonksiyonlar geometrik veya baska yollardan da tanimlanabilirler ve bu bagintilar o yollardan da cikarilabilir Bu fonksiyonlar arasindaki bircok baginti sayfasinda gorulebilir Alti trigonometrik fonksiyonun grafigi birim cember ve 8 0 7 radyan acisi icin bir dogru verilmistir 1 Sec 8 Csc 8 olarak etiketlenen noktalar baslangic noktasindan o noktaya kadar olan dogru parcasinin uzunlugunu temsil eder Sin 8 Tan 8 ve 1 x ekseninden baslayan cizginin yukseklikleridir Cos 8 1 and Cot 8 ise baslangictan baslayarak x ekseni boyunca uzunluklardir Fonksiyon Kisaltma IliskiSinus sin sin 8 cos p2 8 displaystyle sin theta cos left frac pi 2 theta right Kosinus cos cos 8 sin p2 8 displaystyle cos theta sin left frac pi 2 theta right Tanjant tan tan 8 sin 8cos 8 cot p2 8 1cot 8 displaystyle tan theta frac sin theta cos theta cot left frac pi 2 theta right frac 1 cot theta Kotanjant cot cot 8 cos 8sin 8 tan p2 8 1tan 8 displaystyle cot theta frac cos theta sin theta tan left frac pi 2 theta right frac 1 tan theta Sekant sec sec 8 1cos 8 csc p2 8 displaystyle sec theta frac 1 cos theta csc left frac pi 2 theta right Kosekant csc veya cosec csc 8 1sin 8 sec p2 8 displaystyle csc theta frac 1 sin theta sec left frac pi 2 theta right Sinus ve Kosinus fonksiyonlari1 f x sin x islevi dik ucgen de karsi dik kenarin hipotenuse oranidir Koordinat Duzleminde y ekseni olarak tabir edilir Bu islevin tanim araligi 1 1 dir Yani sinus fonksiyonunun degeri 1 den kucuk 1 den buyuk olamaz 2 f x cos x islevi dik ucgende Komsu dik kenarin hipotenuse oranidir Koordinat duzleminde x ekseni olarak tabir edilir Tanim araligi f x sinx isleviyle aynidir Sinus ve Kosinus islevleri arasinda Pisagor teoreminden cikarilabilen sin2 x cos2 x 1 displaystyle sin 2 x cos 2 x 1 bagintisi vardir Tanjant ve Kotanjant islevleri3 f x tanx islevi dik ucgende Karsi dik kenarin komsu dik kenara oranidir Koordinat duzleminde Birim cembere x ekseninin pozitif tarafinda teget ve x eksenine diktir Tanim araligi dir Ayrica tan x cot x 1 displaystyle tan x times cot x 1 dir 4 f x cotx islevi dik ucgende Komsu dik kenarin karsi dik kenara oranidir Koordinat duzleminde Birim cembere y ekseninin pozitif yonunde teget ve y eksenine diktir Tanim araligi dir Tanjant ve Kotanjant islevleri arasinda birim cemberde benzerlik yapilarak veya Pisagor teoreminden bulunabilen tan x cot x 1 displaystyle tan x times cot x 1 bagintisi vardir Trigonometrik fonksiyonlarin ozel degerleri Asagidaki tabloda gosterildigi gibi Trigonometrik fonksiyonlarin bazi yaygin olarak kullanilan ozel degerleri vardir Fonksiyon 0 0 displaystyle 0 0 circ p12 15 displaystyle frac pi 12 15 circ p6 30 displaystyle frac pi 6 30 circ p4 45 displaystyle frac pi 4 45 circ p3 60 displaystyle frac pi 3 60 circ 5p12 75 displaystyle frac 5 pi 12 75 circ p2 90 displaystyle frac pi 2 90 circ sin 0 displaystyle 0 6 24 displaystyle frac sqrt 6 sqrt 2 4 12 displaystyle frac 1 2 22 displaystyle frac sqrt 2 2 32 displaystyle frac sqrt 3 2 6 24 displaystyle frac sqrt 6 sqrt 2 4 1 displaystyle 1 cos 1 displaystyle 1 6 24 displaystyle frac sqrt 6 sqrt 2 4 32 displaystyle frac sqrt 3 2 22 displaystyle frac sqrt 2 2 12 displaystyle frac 1 2 6 24 displaystyle frac sqrt 6 sqrt 2 4 0 displaystyle 0 tan 0 displaystyle 0 2 3 displaystyle 2 sqrt 3 33 displaystyle frac sqrt 3 3 1 displaystyle 1 3 displaystyle sqrt 3 2 3 displaystyle 2 sqrt 3 Tanimsizcot Tanimsiz 2 3 displaystyle 2 sqrt 3 3 displaystyle sqrt 3 1 displaystyle 1 33 displaystyle frac sqrt 3 3 2 3 displaystyle 2 sqrt 3 0 displaystyle 0 sec 1 displaystyle 1 6 2 displaystyle sqrt 6 sqrt 2 233 displaystyle frac 2 sqrt 3 3 2 displaystyle sqrt 2 2 displaystyle 2 6 2 displaystyle sqrt 6 sqrt 2 Tanimsizcsc Tanimsiz 6 2 displaystyle sqrt 6 sqrt 2 2 displaystyle 2 2 displaystyle sqrt 2 233 displaystyle frac 2 sqrt 3 3 6 2 displaystyle sqrt 6 sqrt 2 1 displaystyle 1 Diger trigonometrik fonksiyonlarYukarida ifade edilenlerle birlikte daha once hic duymamis olabileceginiz ek trigonometrik fonksiyon aileleri vardir Bunlar sunlari icerir Versine Vercosine Coversine Covercosine Exsecant Excosecant Haversine Havercosine Hacoversine Hacovercosine Bunlar temel uc trigonometrik fonksiyonun temel kombinasyonlari icin basit isimler olup ozdeslikleri asagidaki tabloda verilmistir Fonksiyon Kisaltma OzdeslikVersinus versin 8 1 cos 8 Verkosinus vercosin 8 1 cos 8 Koversinus coversin 8 1 sin 8 Koverkosinus covercosin 8 1 sin 8 Ekssekant exsec 8 sec 8 1Ekskosekant excsc 8 csc 8 1Haversinus haversin 8 versin 8 2Haverkosinus havercosin 8 vercosin 8 2Hakoversinus hacoversin 8 coversin 8 2Hakoverkosinus hacovercosin 8 covercosin 8 2Birim cemberde tanimlarBirim cember Bu alti trigonometrik fonksiyon birim cember de tanimlanabilir yaricapi bir birim olan cemberdir Birim cember tanimi pratik hesaplamada cok yararlar saglar aslinda cogu acilari icin dik ucgeni kullanabiliriz Acilar 0 ve p 2 radyan la sinirli degildir Birim cember butun pozitif ve negatif acilarin trigonometrik degerlerini tanimlar Ayrica tek bir gorsel resim Ayni anda tum onemli ucgenlerin icinde saklanmasini saglar Pisagor teoremi nden yararlanilarak birim cemberde su denklemi kurabiliriz x2 y2 1 displaystyle x 2 y 2 1 Bu resim bazi yaygin acilari negatif ve pozitif yondeki olculeri radyan olculerini icerir x ekseninin pozitif yarisinin orijinden cizilen dogru ile yaptigi aci 8 dir bu birim cemberle kesisir x ve y koordinatlarinin bu kesim noktasi ile kesistigi nokta sirasiyla cos 8 ve sin 8 degerlerine esittir Hipotenus burada 1 e esittir boylece sin 8 y 1 ve cos 8 x 1 olacaktir Bu degerlerin kolay bicimde hafizaya alindigini aklinizda bulundurunuz 120 121 122 123 124 displaystyle frac 1 2 sqrt 0 quad frac 1 2 sqrt 1 quad frac 1 2 sqrt 2 quad frac 1 2 sqrt 3 quad frac 1 2 sqrt 4 15 18º 36º 54 72º ve 75 icin elde edilen degerleri asagidadir sin 15 cos 75 6 24 displaystyle sin 15 circ cos 75 circ dfrac sqrt 6 sqrt 2 4 sin 18 cos 72 5 14 displaystyle sin 18 circ cos 72 circ frac sqrt 5 1 4 sin 36 cos 54 10 254 displaystyle sin 36 circ cos 54 circ frac sqrt 10 2 sqrt 5 4 sin 54 cos 36 5 14 displaystyle sin 54 circ cos 36 circ dfrac sqrt 5 1 4 sin 72 cos 18 10 254 displaystyle sin 72 circ cos 18 circ frac sqrt 10 2 sqrt 5 4 sin 75 cos 15 6 24 displaystyle sin 75 circ cos 15 circ dfrac sqrt 6 sqrt 2 4 3º 6º 9º 81º 84º ve 87º icin degerleri analitik olarak hesaplanabilir sin 3 cos 87 30 10 20 45 6 2 60 12516 displaystyle sin 3 circ cos 87 circ dfrac sqrt 30 sqrt 10 sqrt 20 4 sqrt 5 sqrt 6 sqrt 2 sqrt 60 12 sqrt 5 16 sin 6 cos 84 30 65 5 18 displaystyle sin 6 circ cos 84 circ dfrac sqrt 30 6 sqrt 5 sqrt 5 1 8 sin 9 cos 81 90 18 10 2 20 45 180 36532 displaystyle sin 9 circ cos 81 circ dfrac sqrt 90 sqrt 18 sqrt 10 sqrt 2 sqrt 20 4 sqrt 5 sqrt 180 36 sqrt 5 32 sin 84 cos 6 10 25 15 38 displaystyle sin 84 circ cos 6 circ frac sqrt 10 2 sqrt 5 sqrt 15 sqrt 3 8 sin 87 cos 3 60 125 20 45 30 2 6 1016 displaystyle sin 87 circ cos 3 circ frac sqrt 60 12 sqrt 5 sqrt 20 4 sqrt 5 sqrt 30 sqrt 2 sqrt 6 sqrt 10 16 Sinus ve kosinus fonksiyonlari Kartezyen duzlemde grafikle gosterilebilir 2p ve daha buyuk acilar icin az 2p ve daha kucuk acilar icin cember etrafinda sadece bir daire etrafinda donmeye devam ederler sin ve cos periyodik fonksiyon ve periodu 2p dir sin 8 sin 8 2pk displaystyle sin theta sin left theta 2 pi k right cos 8 cos 8 2pk displaystyle cos theta cos left theta 2 pi k right herhangi bir aci 8 ve herhangi bir tam sayi k dir Seri tanimlariSinus fonksiyonu mavi orijini merkez alan tam bir dongu icin 7 derecedeki pembe Taylor polinomu ile oldukca yakinsanir Trigonometrik fonksiyonlarin Taylor serisi ne acilimlari asagidaki gibidir butun x gercek sayilar icin sin x x x33 x55 x77 n 0 1 nx2n 1 2n 1 cos x 1 x22 x44 x66 n 0 1 nx2n 2n displaystyle begin aligned sin x amp x frac x 3 3 frac x 5 5 frac x 7 7 cdots amp sum n 0 infty frac 1 n x 2n 1 2n 1 cos x amp 1 frac x 2 2 frac x 4 4 frac x 6 6 cdots amp sum n 0 infty frac 1 n x 2n 2n end aligned Bu iki serinin su toplami Euler formulu nu verir cos x i sin x eix Diger serilerde bulunabilir Asagidaki trigonometrik fonksiyonlar icin Unninci dir Bnninci Bernoulli sayisi dir ve En asagida ninci Euler sayisi dir Tanjant tan x n 0 U2n 1x2n 1 2n 1 n 1 1 n 122n 22n 1 B2nx2n 1 2n x 13x3 215x5 17315x7 x lt p2 icin displaystyle begin aligned tan x amp sum n 0 infty frac U 2n 1 x 2n 1 2n 1 amp sum n 1 infty frac 1 n 1 2 2n 2 2n 1 B 2n x 2n 1 2n amp x frac 1 3 x 3 frac 2 15 x 5 frac 17 315 x 7 cdots qquad x lt frac pi 2 text icin end aligned Eger seri tanjant fonksiyonu ilgili faktoriyelleri ile ifade edilecekse kombinatorik yorumlamada kardinal tek sayilarin sonlu sayida permutasyon alternatifleri vardir bunlar tanjant sayilari olarak adlandirilir Kosekant csc x n 0 1 n 12 22n 1 1 B2nx2n 1 2n x 1 16x 7360x3 3115120x5 0 lt x lt p icin displaystyle begin aligned csc x amp sum n 0 infty frac 1 n 1 2 2 2n 1 1 B 2n x 2n 1 2n amp x 1 frac 1 6 x frac 7 360 x 3 frac 31 15120 x 5 cdots qquad 0 lt x lt pi text icin end aligned Secant sec x n 0 U2nx2n 2n n 0 1 nE2nx2n 2n 1 12x2 524x4 61720x6 x lt p2 icin displaystyle begin aligned sec x amp sum n 0 infty frac U 2n x 2n 2n sum n 0 infty frac 1 n E 2n x 2n 2n amp 1 frac 1 2 x 2 frac 5 24 x 4 frac 61 720 x 6 cdots qquad x lt frac pi 2 text icin end aligned Eger seri sekant fonksiyonu ilgili faktoriyelleri ile ifade edilecekse kombinatorik yorumlamada kardinal tek sayilarin sonlu sayida permutasyon alternatifleri vardir bunlar sekant sayilari olarak adlandirilir Kotanjant cot x n 0 1 n22nB2nx2n 1 2n x 1 13x 145x3 2945x5 0 lt x lt p icin displaystyle begin aligned cot x amp sum n 0 infty frac 1 n 2 2n B 2n x 2n 1 2n amp x 1 frac 1 3 x frac 1 45 x 3 frac 2 945 x 5 cdots qquad 0 lt x lt pi text icin end aligned kotanjant fonksiyonu ve ters fonksiyonlar icin p cot px limN n NN1x n displaystyle pi cdot cot pi x lim N to infty sum n N N frac 1 x n Bu esitlik hilesi ile ispat edilir n displaystyle n inci ve n displaystyle n inci terimleri birlestirilerek mutlak yakinsak seri p cot px 1x n 1 2xx2 n2 displaystyle pi cdot cot pi x frac 1 x sum n 1 infty frac 2x x 2 n 2 Ustel fonksiyonlar ve karmasik sayilarla iliskisi Euler formulunun uc boyutlu helisle gosterimi birim cemberin 2 D parcasi ile basliyor sin displaystyle sin ve cos displaystyle cos 8 displaystyle theta yerine displaystyle t displaystyle t ei8 cos 8 isin 8 displaystyle e i theta cos theta i sin theta Bu esitlik Euler formuludur Karmasik analizin geometrik yorumlanmasinin esasini olusturur Ornek olarak Karmasik duzlem de birim cemberin e ix parametrizasyonu gibi Buradaki paramatreler cos ve sin dir Euler formulu ile asagidaki sin ve cos yazilabilir sin 8 ei8 e i82i displaystyle sin theta frac e i theta e i theta 2i cos 8 ei8 e i82 displaystyle cos theta frac e i theta e i theta 2 Dahasi trigonometrik fonksiyonlarin bu karmasik argumanlari icin z tanimini saglar sin z n 0 1 n 2n 1 z2n 1 eiz e iz2i sinh iz i displaystyle sin z sum n 0 infty frac 1 n 2n 1 z 2n 1 frac e iz e iz 2i frac sinh left iz right i cos z n 0 1 n 2n z2n eiz e iz2 cosh iz displaystyle cos z sum n 0 infty frac 1 n 2n z 2n frac e iz e iz 2 cosh left iz right burada i 2 1 sin ve cos tam fonksiyon dur Ayrica x saf gerceldir cos x Re eix displaystyle cos x operatorname Re e ix sin x Im eix displaystyle sin x operatorname Im e ix Ayrica argumanlari gercek ve sanal kisimlari bakimindan karmasik sinus ve kosinus fonksiyonlari ifade etmek bazen yararlidir sin x iy sin xcosh y icos xsinh y displaystyle sin x iy sin x cosh y i cos x sinh y cos x iy cos xcosh y isin xsinh y displaystyle cos x iy cos x cosh y i sin x sinh y Bu sin cos fonksiyonlarindan yararlanilarak hiperbolik gercek sinh cosh karsiliklari bulunabilir Karmasik grafik Aralik degerinin parlakligin buyuklugu mutlak degeri gosterir Parlakligi siyah olan deger sifirdir Renk tonu pozitif reel eksenle olculen arguman veya aci ile degisir Karmasik islevler icin renk haritasi Olcek sinh kullanilarak yapilir Ayrica bakinizTrigonometrinin ana hatlari Hiperbolik fonksiyon Birim vektor cos yon aciklamasi Euler formulu kose acilari bir genellemesi tanjant fonksiyonu tanimi icin birNotlar a b c d Abramowitz Milton and Irene A Stegun p 74 See Ahlfors pages 43 44 Abramowitz Weisstein a b Stanley Enumerative Combinatorics Vol I page 149 2000 Proofs from THE BOOK Second Springer Verlag s 149 ISBN 978 3 642 00855 9 20 Subat 2012 tarihinde kaynagindan Erisim tarihi 27 Haziran 2012 Remmert Reinhold 1991 Theory of complex functions Springer s 327 ISBN 0 387 97195 5 18 Ocak 2012 tarihinde kaynagindan Erisim tarihi 27 Haziran 2012 Extract of page 327 7 Haziran 2013 tarihinde Wayback Machine sitesinde KaynakcaAbramowitz Milton and Irene A Stegun Dover New York 1964 ISBN 0 486 61272 4 Lars Ahlfors Complex Analysis an introduction to the theory of analytic functions of one complex variable second edition New York 1966 Boyer Carl B A History of Mathematics John Wiley amp Sons Inc 2nd edition 1991 ISBN 0 471 54397 7 Gal Shmuel and Bachelis Boris An accurate elementary mathematical library for the IEEE floating point standard ACM Transaction on Mathematical Software 1991 Joseph George G The Crest of the Peacock Non European Roots of Mathematics 2nd ed Penguin Books London 2000 ISBN 0 691 00659 8 Kantabutra Vitit On hardware for computing exponential and trigonometric functions IEEE Trans Computers 45 3 328 339 1996 Maor Eli Princeton Univ Press 1998 Reprint edition February 25 2002 ISBN 0 691 09541 8 Needham Tristan to Visual Complex Analysis2 Haziran 2004 tarihinde Wayback Machine sitesinde Oxford University Press 1999 ISBN 0 19 853446 9 O Connor J J and E F Robertson MacTutor History of Mathematics archive 1996 O Connor J J and E F Robertson Madhava of Sangamagramma 26 Subat 2006 tarihinde Wayback Machine sitesinde MacTutor History of Mathematics archive 2000 Pearce Ian G Madhava of Sangamagramma 5 Mayis 2006 tarihinde Wayback Machine sitesinde MacTutor History of Mathematics archive 2002 Weisstein Eric W Tangent 19 Temmuz 2006 tarihinde Wayback Machine sitesinde from MathWorld accessed 21 January 2006 Dis baglantilarVikikitap Vikikitapta bu konu hakkinda daha fazla bilgi var Trigonometry Visionlearning Module on Wave Mathematics18 Mart 2008 tarihinde Wayback Machine sitesinde Visualization of the unit circle trigonometric and hyperbolic functions Dave s draggable diagram 15 Haziran 2008 tarihinde Wayback Machine sitesinde Requires java browser plugin
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans