Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
| Genel görelilik |
 |
| İlgili başlıklar |
| düzenle |
Genel görelilikte, Van Stockum tozu Einstein alan denklemlerinin silindirik simetri ekseni etrafında dönen oluşturduğu yer çekimi alanı için kesin sonucudur. Tozun yoğunluğu eksenin uzaklığıyla beraber arttığı için çözüm oldukça yapay olmakla kalmaz, aynı zamanda genel görelilikteki bilinen en basit çözümlerden olmakla beraber aynı zamanda Pedagojik olarak önemli örneklerden biri olarak gösterilir.
Bu çözüm ismini 'dan almıştır, kendisi 1937 yılında, 'un 1924 yılında keşfettiği olayın bağımsızlığını yeniden keşfetti.
Türetme
Bu çözümü elde etme yollarından biri de katı rotasyon içindeki silindirik olarak harika simetriye bakmaktır (akışkan çözümleri). Dünya hatları ile zamansal uyumlu sıvı parçacıkların sıfırdan farklı girdap olan ancak genişleme ve kesme kaybolan formunda olduğunu kabul ediyoruz. (İşin aslı toz parçacıkları kuvvet hissetmedikleri için, bunun bir zamansal jeodezik uyum olduğu ortaya çıkacak ama bunu ileri işlemlerde böyle kabul etmemize gerek yoktur).
Tahmin yürüterek yaptığımız basit hesaplamalar aşağıdaki sisteme ihtiyaç duyar, bu da iki tane belirlenmemiş 
Yanlış anlaşılmalardan kaçınmak için, aşağıdaki işlemi uygulamalıyız:
Böylece metrik tensörü iki tanımlanmayan faktör cinsinden verir:
Verilerimizi çarparsak
Bu sisteme göre iki tanımlanmayan fonksiyon cinsinden Einstein tensörünü bulmuş oluruz ve akışkan çözümlerinin sonucundan zaman benzeri birim vektör 
Bu aşağıdaki koşulları vermektedir:


Bu sistemin sadece 
Özellik
Bizim çerçeveye göre Einstein tensör Computing aslında basınç kaybolur gösterir, bu yüzden bir toz çözümümüz var. Toz kütle yoğunluğu bek çıkıyor
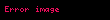
Gösterilen çözersek aşağıdakiler tarafından oluşturulan
Burada, 
Gödel toz çözeltisi aksine, van Stockum toz parçacıkları geometrik seçkin eksen etrafında dönen vardır toz unutmayın.
Denildiği gibi 
Bu hatta Comoving grafikte da toz partiküllerinin dünya hatları aslında parçacıklar simetri ekseni etrafında döndürülür toz olarak birbirinden yaklaşık büküm vardır, dikey çizgiler olarak görünür olduğu anlamına gelir. Toza bir küçük top yap evrimi takip. Başka bir deyişle, bunun kendi ekseni çevresinde döner (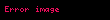

Tidal tensörü;
bu toz parçacıkları üzerinde sürme gözlemci dönme düzlemi içinde izotropik gelgit gerilme geçirmektedir göstermektedir. Magnetogravitic tensör olduğunu
Aşikar paradox
Bu alt başlığın genişletilmesi gerekiyor. Sayfayı düzenleyerek yardımcı olabilirsiniz. |
Gerçek Paradoks
Dışa doğru gittiğimizde, görüyoruz ki daha büyük radii'li horizontal yuvarlaklar kapalı zamanımsı (zaman benzeri) eğridirler (curve) (yani büyük radiili horizanlar yuvarlaklar – kapalı zamanımsı eğri). Bu CTC lerin paradoksal yapısına ilk olarak van Stockum dikkat çekmişti: World lineları kapalı zamanımsı eğri oluşturan gözlemciler rahatça kendi geçmişlerini ziyaret edebilirler veya etkileyebilirler. Daha da kötüsü, böyle bir gözlemciyi, üçüncü hayatında (lifetime) örneğin hızlanmayı durdurmaya karar vermesini engelleyebilecek hiçbir şey yoktur ve bu durum ona bir den fazla biyografi verir
Kapalı zamansı (timelike) kıvrımlar genel göreliliğin birçok çözümünde ortaya çıkabilirler ve ortak ortaya çıkışları/görünüşleri bu teoriye en sorunsal teorik itirazlardan biridir. Ancak çok az fizikçi böyle itirazların temelinde tamamen genel göreliliği kullanmayı reddederler. Tercihen çoğu pragmatik tutum alarak her ne zaman onunla (genel görelilik) kurtulmak isterse teorinin birçok astrofiziksel durumda göreceli basitliği ve iyi kurulmuş güvenilirliği sayesinde göreceli olarak mantıklı gelir. Bu birçok fizikçinin her gün Newton Fiziği'ni kullanmasına benzer değildir, öyle olsa bile onlar bunun Galilei kinematiklerinin görelilik kinematikleri tarafından "yıkıldığının" çok iyi farkındalar
Ayrıca bakınız
Kaynakça
- Lanczos, Cornelius (1924). "Über eine stationäre Kosmologie im Sinne der Einsteinschen Gravitationstheorie". Zeitschrift für Physik. Cilt 21. s. 73. Bibcode:1924ZPhy...21...73L. doi:10.1007/BF01328251. Lanczos's paper announcing the first discovery of this solution.
- van Stockum, Willem Jacob (1937). "The gravitational field of a distribution of particles rotating around an axis of symmetry". Proc. Roy. Soc. Edinburgh A. Cilt 57. s. 135. Van Stockum's paper announcing his rediscovery of this solution.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Vikipedi nin kalite standartlarina ulasabilmesi icin bu maddenin veya bir bolumundeki ansiklopedik olmayan icerigin temizlenmesi gerekmektedir Goruslerinizi lutfen tartisma sayfasinda belirtiniz Nisan 2017 Bu maddenin iceriginin Turkcelestirilmesi veya Turkce dilbilgisi ve kurallari dogrultusunda duzeltilmesi gerekmektedir Bu maddedeki yazim ve noktalama yanlislari ya da anlatim bozukluklari giderilmelidir Yabanci sozcukler yerine Turkce karsiliklarinin kullanilmasi karakter hatalarinin duzeltilmesi dilbilgisi hatalarinin duzeltilmesi vs Duzenleme yapildiktan sonra bu sablon kaldirilmalidir Bu maddedeki uslubun ansiklopedik bir yazidan beklenen resmi ve ciddi usluba uygun olmadigi dusunulmektedir Maddeyi gelistirerek ya da konuyla ilgili tartismaya katilarak Vikipedi ye katkida bulunabilirsiniz Genel gorelilikGenel bakis Tarihce Testler Einstein denklemleri Esdegerlik ilkesi Kara delik Kutlecekimsel dalga Kutlecekimsel mercek Olay ufku Schwarzschild cozumu TekillikIlgili basliklarAlbert Einstein Astrofizik Kozmoloji Kutlecekim Ozel gorelilik Riemann geometrisi Stephen Hawkingduzenle Genel gorelilikte Van Stockum tozu Einstein alan denklemlerinin silindirik simetri ekseni etrafinda donen olusturdugu yer cekimi alani icin kesin sonucudur Tozun yogunlugu eksenin uzakligiyla beraber arttigi icin cozum oldukca yapay olmakla kalmaz ayni zamanda genel gorelilikteki bilinen en basit cozumlerden olmakla beraber ayni zamanda Pedagojik olarak onemli orneklerden biri olarak gosterilir Bu cozum ismini dan almistir kendisi 1937 yilinda un 1924 yilinda kesfettigi olayin bagimsizligini yeniden kesfetti TuretmeBu cozumu elde etme yollarindan biri de kati rotasyon icindeki silindirik olarak harika simetriye bakmaktir akiskan cozumleri Dunya hatlari ile zamansal uyumlu sivi parcaciklarin sifirdan farkli girdap olan ancak genisleme ve kesme kaybolan formunda oldugunu kabul ediyoruz Isin asli toz parcaciklari kuvvet hissetmedikleri icin bunun bir zamansal jeodezik uyum oldugu ortaya cikacak ama bunu ileri islemlerde boyle kabul etmemize gerek yoktur Tahmin yuruterek yaptigimiz basit hesaplamalar asagidaki sisteme ihtiyac duyar bu da iki tane belirlenmemis r displaystyle r ye bagli fonksiyonu icerir e 0 t e 1 f r z e 2 f r r e 3 1r ϕ h r t displaystyle vec e 0 partial t vec e 1 f r partial z vec e 2 f r partial r vec e 3 frac 1 r partial phi h r partial t Yanlis anlasilmalardan kacinmak icin asagidaki islemi uygulamaliyiz s0 dt h r rdϕ s1 1f r dz s2 1f r dr s3 rdϕ displaystyle sigma 0 dt h r r d phi sigma 1 frac 1 f r dz sigma 2 frac 1 f r dr sigma 3 rd phi Boylece metrik tensoru iki tanimlanmayan faktor cinsinden verir g s0 s0 s1 s1 s2 s2 s3 s3 displaystyle g sigma 0 otimes sigma 0 sigma 1 otimes sigma 1 sigma 2 otimes sigma 2 sigma 3 otimes sigma 3 Verilerimizi carparsak ds2 dt2 2h r rdtdϕ 1 h r 2 r2dϕ2 dz2 dr2f r 2 displaystyle ds 2 dt 2 2h r r dt d phi 1 h r 2 r 2 d phi 2 frac dz 2 dr 2 f r 2 lt t z lt 0 lt r lt p lt ϕ lt p displaystyle infty lt t z lt infty 0 lt r lt infty pi lt phi lt pi Bu sisteme gore iki tanimlanmayan fonksiyon cinsinden Einstein tensorunu bulmus oluruz ve akiskan cozumlerinin sonucundan zaman benzeri birim vektor e 0 displaystyle vec e 0 olustururuz sivi parcacigina tanjant cizgisi olan her yer icin Boylece su sonuca ulasiriz Gm n 8pmdiag 1 0 0 0 8ppdiag 0 1 1 1 displaystyle G hat m hat n 8 pi mu operatorname diag 1 0 0 0 8 pi p operatorname diag 0 1 1 1 Bu asagidaki kosullari vermektedir f f 2f f r h 2 2h hr h2r2 4f rf displaystyle f prime prime frac f prime 2 f frac f prime r h prime 2 frac 2h prime h r frac h 2 r 2 frac 4f prime r f f displaystyle f yi cozup h displaystyle h degeri icin uygun sistemler Van Stockum cozumunu tanimlamaktadir e 0 t e 1 exp a2r2 2 z e 2 exp a2r2 2 r e 3 1r ϕ ar t displaystyle vec e 0 partial t vec e 1 exp a 2 r 2 2 partial z vec e 2 exp a 2 r 2 2 partial r vec e 3 frac 1 r partial phi ar partial t Bu sistemin sadece r gt 0 displaystyle r gt 0 da tanimli oldugu unutulmamalidir OzellikBizim cerceveye gore Einstein tensor Computing aslinda basinc kaybolur gosterir bu yuzden bir toz cozumumuz var Toz kutle yogunlugu bek cikiyor m a22pexp a2r2 displaystyle mu frac a 2 2 pi exp a 2 r 2 r 0 displaystyle r 0 simetri ekseninde bu sonludur ama yogunluk yaricap ile beraber artar ama maalesef bu astrofizigin sinirladigi ozelliklerden biridir Gosterilen cozersek asagidakiler tarafindan olusturulan 3 1 t 3 2 z 3 3 ϕ displaystyle vec xi 1 partial t vec xi 2 partial z vec xi 3 partial phi Burada 3 1 displaystyle vec xi 1 sifirdan farkli girdap vardir bu yuzden hem de bu eksen etrafinda silindirik simetri ve donme ekseni boyunca ceviri altinda toz partikullerinin dunya cizgisinde ceviri altinda sabit bir uzay degismeyen var Godel toz cozeltisi aksine van Stockum toz parcaciklari geometrik seckin eksen etrafinda donen vardir toz unutmayin Denildigi gibi e 0 displaystyle vec e 0 bileseni kaybolur ama vorticity vektoru su sekildedir W aexp a2r2 2 e 1 displaystyle vec Omega a exp a 2 r 2 2 vec e 1 Bu hatta Comoving grafikte da toz partikullerinin dunya hatlari aslinda parcaciklar simetri ekseni etrafinda dondurulur toz olarak birbirinden yaklasik bukum vardir dikey cizgiler olarak gorunur oldugu anlamina gelir Toza bir kucuk top yap evrimi takip Baska bir deyisle bunun kendi ekseni cevresinde doner r 0 displaystyle r 0 a parallel ancak diger kesme veya genisletmek degildir Ikincisi ozellikle biz sert donme ile ne demek tanimlar Cevri vektorunun buyuklugu sadece bir olur eksen kendisini dikkat edin a displaystyle a Tidal tensoru Em n a2exp a2r2 diag 0 1 1 displaystyle E hat m hat n a 2 exp a 2 r 2 operatorname diag 0 1 1 bu toz parcaciklari uzerinde surme gozlemci donme duzlemi icinde izotropik gelgit gerilme gecirmektedir gostermektedir Magnetogravitic tensor oldugunu Bm n a3exp a2r2 010100000 displaystyle B hat m hat n a 3 exp a 2 r 2 left begin matrix 0 amp 1 amp 0 1 amp 0 amp 0 0 amp 0 amp 0 end matrix right Asikar paradoxBu alt basligin genisletilmesi gerekiyor Sayfayi duzenleyerek yardimci olabilirsiniz Gercek ParadoksDisa dogru gittigimizde goruyoruz ki daha buyuk radii li horizontal yuvarlaklar kapali zamanimsi zaman benzeri egridirler curve yani buyuk radiili horizanlar yuvarlaklar kapali zamanimsi egri Bu CTC lerin paradoksal yapisina ilk olarak van Stockum dikkat cekmisti World linelari kapali zamanimsi egri olusturan gozlemciler rahatca kendi gecmislerini ziyaret edebilirler veya etkileyebilirler Daha da kotusu boyle bir gozlemciyi ucuncu hayatinda lifetime ornegin hizlanmayi durdurmaya karar vermesini engelleyebilecek hicbir sey yoktur ve bu durum ona bir den fazla biyografi verir Kapali zamansi timelike kivrimlar genel goreliligin bircok cozumunde ortaya cikabilirler ve ortak ortaya cikislari gorunusleri bu teoriye en sorunsal teorik itirazlardan biridir Ancak cok az fizikci boyle itirazlarin temelinde tamamen genel goreliligi kullanmayi reddederler Tercihen cogu pragmatik tutum alarak her ne zaman onunla genel gorelilik kurtulmak isterse teorinin bircok astrofiziksel durumda goreceli basitligi ve iyi kurulmus guvenilirligi sayesinde goreceli olarak mantikli gelir Bu bircok fizikcinin her gun Newton Fizigi ni kullanmasina benzer degildir oyle olsa bile onlar bunun Galilei kinematiklerinin gorelilik kinematikleri tarafindan yikildiginin cok iyi farkindalarAyrica bakinizKaynakcaLanczos Cornelius 1924 Uber eine stationare Kosmologie im Sinne der Einsteinschen Gravitationstheorie Zeitschrift fur Physik Cilt 21 s 73 Bibcode 1924ZPhy 21 73L doi 10 1007 BF01328251 Lanczos s paper announcing the first discovery of this solution van Stockum Willem Jacob 1937 The gravitational field of a distribution of particles rotating around an axis of symmetry Proc Roy Soc Edinburgh A Cilt 57 s 135 Van Stockum s paper announcing his rediscovery of this solution
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans












