İstatistiksel ölçülerinin bilgisayar ile yapılan hesaplanmalarında varyans hesaplanması için kullanılan algoritmalar pratik sonuçlar elde edilmesinde önemli rol oynamaktadırlar. Varyansın hesaplanması için işe yarar bilgisayar algoritmalarının tasarlanmasında ana sorun varyans formüllerinin veri kare toplamlarının hesaplanmasını gerektirmesindedir. Bu işlem yapılırken problemleri ve özellikle büyük veri değerleri bulunuyorsa problemleri ortaya çıkması çok muhtemeldir.
Ancak, 2014 yılında yayınlanan "İstatistikte Altın Oran" adlı bir kitapta, operatörü yerine, üstel bir işlem içermeyen, sadece dört işlem ve sınırlı toplama operatörü ile hesaplanabilen bir sapma metodolojisi tanımlanmıştır. Tanımlanan bu sapma'nın en dikkat çekici özelliği, ortalama'nın sağı ve solu için, birbirinden bağımsız iki ayrı sapma üretmesidir.
I. Naif algoritma
Tüm bir anakütle veri dizisi için varyansın hesaplanması için formül şudur:
Bir sonsuz olmayan n gözlem hacminde bir örneklem veri dizisi kullanarak anakütle varyansının bir yansız kestirim değerini bulmak için formül şöyle ifade edilir:
Bu formüller kullanılarak varyans kestirimi hesaplamak için bir naif algoritma için şöyle verilir:
n = 0 toplam = 0 toplam_kare = 0 for veri olan her x: n = n + 1 toplam = toplam + x toplam_kare = toplam_kare + x*x end for ortalama = toplam/n varyans = (toplam_kare - toplam*ortalama)/(n - 1)
Bu algoritma bir sonlu anakutle verileri için varyansin hesaplanmasına hemen adapte edilebilir: en son satırda ki n - 1 ile bolum yapılacağına n ile bolum yapılır.
toplam_kare ve toplam * ortalama birbirine hemen yakın sayılar olabilir. Bu nedenle sonucun kesinliği hesaplamada kullanılan aritmetiğin doğal kesinliğinden daha az olabilir. Eğer varyans değeri elde edilen veri toplamına karşıt olarak daha küçük ise, bu sorun daha da şiddetle ortaya çıkar.
II. İki-geçişli algoritma
Varyans için değişik bir formül kullanan diğer bir yaklaşım şu sözde kod ile verilmiştir:
n = 0 toplam1 = 0 for veri olan her x: n = n + 1 toplam1 = toplam1 + x end for ortalama = toplam1/n toplam2 = 0 for veri olan her x: toplam2 = toplam2 + (x - ortalama)^2 end for varyans = toplam2/(n - 1)
IIa. Düzeltilmiş toplam şekli
Yukarıda verilen algoritmanın düzeltilmiş toplam şekli şöyle verilir:
n = 0 toplam1 = 0 for veri olan her x: n = n + 1 toplam1 = toplam1 + x end for ortalama = toplam1/n toplam2 = 0 toplamc = 0 for veri olan her x: toplam2 = toplam2 + (x - ortalama)^2 toplamc = toplamc + (x - ortalama) end for varyans = (toplam2 - toplamc^2/n)/(n - 1)
III. On-line algoritması
Gereken yenileştirme için bulunabilecek daha uygun bir işlemin (cari) ortalamadan farkların karelerinin toplamını bulmak olduğu anlaşılmıştır; bu değer 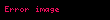
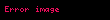
Sayısal olarak daha kararlı bir algoritma aşağıda verilmiştir. Bu algoritma ortalama hesaplamak için kullanılmak niyetiyle Knuth (1998) tarafından verilmiş ve orada ilk defa Welford(1962) tarafından ortaya atıldığı bildirilmiştir.
n = 0 ortalama = 0 M2 = 0 for veri olan her x: n = n + 1 delta = x - ortalama ortalama = ortalama + delta/n M2 = M2 + delta*(x - ortalama) // Bu terim ortalama için yeni değeri kullanır end for varyans_n = M2/n varyans = M2/(n - 1)
IV. Ağırlıklı küçük artışlı algoritma
Eğer gözlemler için değişik ağırlıklar verilmişse, West (1979) şu küçük artışlı algoritmanın kullanılabileceğini bildirmiştir:
n = 0 for veri olan her x: if n=0 then n = 1 ortalama = x S = 0 toplamagırlık = agırlık else n = n + 1 temp = agırlık + toplamagırlık S = S + sumweight*agırlık*(x-ortalama)^2 / temp ortalama = ortalama + (x-ortalama)*agırlık / temp toplamagırlık = temp end if end for Varyans = S * n / ((n-1)*toplamagırlık) // eğer veri dizisi anakütle içinse n/(n-1) kullanılmaz.
V. Paralel algoritma
Chan, Golub ve LeVeque (1979) hazırladıkları bir raporda yukarıda verilen III. On-line Algoritmasının bir örneklem olan 
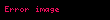
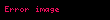
.
Bu bazı hallerde daha kullanışlı olabilmektedir. Örneğin girdinin ayrılabilir parçalarına çoklu kompüter işlem birimlerinin kullanılması imkânını sağlayabilir.
V.a. Üst seviyede istatistikler
Örneklem verileri için üst seviyede istatistikler olan çarpıklık ve basıklık ölçülerini bulmak için Terriberry Chen'in üçüncü ve dördüncü merkezsel moment bulmak için ortaya attığı formülü daha uygun bir şekle şöyle değiştirmiştir.::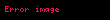
Burada yine, 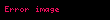

: çarpıklık,
: basıklık.
Küçük artışlı hallerde (yani 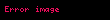
Burada dikkati çeken nokta, 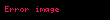
Örnek
Kullanılan kompüterde bütün "floating" nokta operasyonlarının (IEEE 754 çifte-hassiyetli) aritmetik ile yapıldığı varsayılsın. Sonsuz büyüklükte bir anakütleden n=5 büyüklüğünde bir örneklem olarak
- 4, 7, 13, 16
veri seti elde edildiğini düşünelim. Bu örneklem için örneklem ortalaması 10 olur ve yanlı olmayan anakütle varyans kestirimi 30dur. Hem "I. naif Algoritma" hem de "II. iki geçişli Algoritma" bu değerleri doğru olarak hesaplamaktadırlar.
Şimdi örnekleme olarak şu veri setini alalım:
,
,
,
Bu örneklemin de, birinci örneklem gibi ayni varyans kestirimine sahip olması gerekir. "II. Algoritma" bu varyansı doğru olarak hesaplamaktadır. Fakat "I. Algoritma" sonuç olarak tam 30 yerine 29.333333333333332 sonucu verir. Bu dakiklik kaybının belki kabul edilebilir tolerans olduğu ve "I. Algoritma" kullanılmasının nispeten önemsiz bir hata doğurduğu söylenebilir.
Fakat bu "I. Algoritma" hesaplamasında çok önemli bir eksiklik ve hataya işaret etmektedir. Bu sefer örneklem olarak şunu alalım:
,
,
,
Yine "II. Algoritma" doğru anakütle varyans kestirimi olarak 30 gösterir. Ama "I. Algoritma" kullanılınca elde edilen kestirim hesabı -170.66666666666666 olarak verilir. Bu çok önemli ve yapılmaması gereken bir hatadır; çünkü kavram olarak tanımlamayla varyans değerinin hiçbir zaman negatif olmaması gerekir.
Ayrıca bakınız
Kaynakça
- ^ Mehmet Güven GÜNVER, Prof. Dr. Mustafa Şükrü ŞENOCAK, Doç Dr. Suphi VEHİD, İstatistikte Altın Oran, Türkmen Kitabevi, 2014, ISBN : 9786054749409
- ^ Knuth,D.E. (1998). The Art of Computer Programming, V.2: Seminumerical Algorithms, 3. ed., p. 232. Boston: Addison-Wesley.
- ^ Welford,B.P. (1962). "Note on a method for calculating corrected sums of squares and products". Technometrics C.4 No.3 say.419–420. [1]
- ^ D. H. D. West (1979). , 22, 9, 532-535: Updating Mean and Variance Estimates: An Improved Method
- ^ Terriberry,T.B. (2007), Computing Higher-Order Moments Online url=http://people.xiph.org/~tterribe/notes/homs.html 23 Nisan 2014 tarihinde Wayback Machine sitesinde .
Dış bağlantılar
- Eric W. Weisstein, Sample Variance Computation (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Istatistiksel olculerinin bilgisayar ile yapilan hesaplanmalarinda varyans hesaplanmasi icin kullanilan algoritmalar pratik sonuclar elde edilmesinde onemli rol oynamaktadirlar Varyansin hesaplanmasi icin ise yarar bilgisayar algoritmalarinin tasarlanmasinda ana sorun varyans formullerinin veri kare toplamlarinin hesaplanmasini gerektirmesindedir Bu islem yapilirken problemleri ve ozellikle buyuk veri degerleri bulunuyorsa problemleri ortaya cikmasi cok muhtemeldir Ancak 2014 yilinda yayinlanan Istatistikte Altin Oran adli bir kitapta operatoru yerine ustel bir islem icermeyen sadece dort islem ve sinirli toplama operatoru ile hesaplanabilen bir sapma metodolojisi tanimlanmistir Tanimlanan bu sapma nin en dikkat cekici ozelligi ortalama nin sagi ve solu icin birbirinden bagimsiz iki ayri sapma uretmesidir I Naif algoritmaTum bir anakutle veri dizisi icin varyansin hesaplanmasi icin formul sudur s2 i 1nxi2 i 1nxi 2 nn displaystyle sigma 2 displaystyle frac sum i 1 n x i 2 sum i 1 n x i 2 n n Bir sonsuz olmayan n gozlem hacminde bir orneklem veri dizisi kullanarak anakutle varyansinin bir yansiz kestirim degerini bulmak icin formul soyle ifade edilir s2 i 1nxi2 i 1nxi 2 nn 1 displaystyle s 2 displaystyle frac sum i 1 n x i 2 sum i 1 n x i 2 n n 1 Bu formuller kullanilarak varyans kestirimi hesaplamak icin bir naif algoritma icin soyle verilir n 0 toplam 0 toplam kare 0 for veri olan her x n n 1 toplam toplam x toplam kare toplam kare x x end for ortalama toplam n varyans toplam kare toplam ortalama n 1 Bu algoritma bir sonlu anakutle verileri icin varyansin hesaplanmasina hemen adapte edilebilir en son satirda ki n 1 ile bolum yapilacagina n ile bolum yapilir toplam kare ve toplam ortalama birbirine hemen yakin sayilar olabilir Bu nedenle sonucun kesinligi hesaplamada kullanilan aritmetigin dogal kesinliginden daha az olabilir Eger varyans degeri elde edilen veri toplamina karsit olarak daha kucuk ise bu sorun daha da siddetle ortaya cikar II Iki gecisli algoritmaVaryans icin degisik bir formul kullanan diger bir yaklasim su sozde kod ile verilmistir n 0 toplam1 0 for veri olan her x n n 1 toplam1 toplam1 x end for ortalama toplam1 n toplam2 0 for veri olan her x toplam2 toplam2 x ortalama 2 end for varyans toplam2 n 1 IIa Duzeltilmis toplam sekli Yukarida verilen algoritmanin duzeltilmis toplam sekli soyle verilir n 0 toplam1 0 for veri olan her x n n 1 toplam1 toplam1 x end for ortalama toplam1 n toplam2 0 toplamc 0 for veri olan her x toplam2 toplam2 x ortalama 2 toplamc toplamc x ortalama end for varyans toplam2 toplamc 2 n n 1 III On line algoritmasimyeni nmeski xyenin 1 meski xyeni meskin 1 displaystyle m mathrm yeni frac n m mathrm eski x mathrm yeni n 1 m mathrm eski frac x mathrm yeni m mathrm eski n 1 sn 1 yeni2 n 1 sn 1 eski2 xyeni myeni xyeni meski nn gt 0 displaystyle s mathrm n 1 yeni 2 frac n 1 s mathrm n 1 eski 2 x mathrm yeni m mathrm yeni x mathrm yeni m mathrm eski n mathrm n gt 0 sn yeni2 n sn eski2 xyeni myeni xyeni meski n 1 displaystyle s mathrm n yeni 2 frac n s mathrm n eski 2 x mathrm yeni m mathrm yeni x mathrm yeni m mathrm eski n 1 Gereken yenilestirme icin bulunabilecek daha uygun bir islemin cari ortalamadan farklarin karelerinin toplamini bulmak oldugu anlasilmistir bu deger i 1n xi m 2 displaystyle sum i 1 n x i m 2 olup burada M2 displaystyle M 2 olarak gosterilmektedir M2 yeni M2 eski xnew meski xyeni myeni displaystyle M mathrm 2 yeni M mathrm 2 eski x mathrm new m mathrm eski x mathrm yeni m mathrm yeni sn2 M2n displaystyle s mathrm n 2 frac M 2 n sn 12 M2n 1 displaystyle s mathrm n 1 2 frac M 2 n 1 Sayisal olarak daha kararli bir algoritma asagida verilmistir Bu algoritma ortalama hesaplamak icin kullanilmak niyetiyle Knuth 1998 tarafindan verilmis ve orada ilk defa Welford 1962 tarafindan ortaya atildigi bildirilmistir n 0 ortalama 0 M2 0 for veri olan her x n n 1 delta x ortalama ortalama ortalama delta n M2 M2 delta x ortalama Bu terim ortalama icin yeni degeri kullanir end for varyans n M2 n varyans M2 n 1 IV Agirlikli kucuk artisli algoritmaEger gozlemler icin degisik agirliklar verilmisse West 1979 su kucuk artisli algoritmanin kullanilabilecegini bildirmistir n 0 for veri olan her x if n 0 then n 1 ortalama x S 0 toplamagirlik agirlik else n n 1 temp agirlik toplamagirlik S S sumweight agirlik x ortalama 2 temp ortalama ortalama x ortalama agirlik temp toplamagirlik temp end if end for Varyans S n n 1 toplamagirlik eger veri dizisi anakutle icinse n n 1 kullanilmaz V Paralel algoritmaChan Golub ve LeVeque 1979 hazirladiklari bir raporda yukarida verilen III On line Algoritmasinin bir orneklem olan X displaystyle X i herhangi iki tane XA displaystyle X A ve XB displaystyle X B setlerine ayirmak icin isleme konabilen bir algoritmanin ozel bir hali oldugunu bildirmislerdir d mB mA displaystyle delta m B m A mX mA d NBNX displaystyle m X m A delta cdot frac N B N X M2X M2A M2B d2 NANBNX displaystyle M 2 X M 2 A M 2 B delta 2 cdot frac N A N B N X Bu bazi hallerde daha kullanisli olabilmektedir Ornegin girdinin ayrilabilir parcalarina coklu komputer islem birimlerinin kullanilmasi imkanini saglayabilir V a Ust seviyede istatistikler Orneklem verileri icin ust seviyede istatistikler olan carpiklik ve basiklik olculerini bulmak icin Terriberry Chen in ucuncu ve dorduncu merkezsel moment bulmak icin ortaya attigi formulu daha uygun bir sekle soyle degistirmistir M3X M3A M3B d3NANB NA NB NX 2 3dNAM2B NBM2ANX displaystyle M 3 X M 3 A M 3 B delta 3 frac N A N B N A N B N X 2 3 delta frac N A M 2 B N B M 2 A N X M4X M4A M4B d4NANB NA 2 NANB NB 2 NX 3 6d2 NA 2M2B NB 2M2A NX 2 4dNAM3B NBM3ANX displaystyle begin aligned M 4 X M 4 A M 4 B amp delta 4 frac N A N B left N A 2 N A N B N B 2 right N X 3 amp 6 delta 2 frac N A 2 M 2 B N B 2 M 2 A N X 2 4 delta frac N A M 3 B N B M 3 A N X end aligned Burada yine Mk displaystyle M k verilerin ortalamadan farklarinin ustel degerlerinin toplamlaridir yani S x x k displaystyle Sigma x overline x k olur Bu degerler kullanilarak carpiklik ve basiklik olculeri soyle bulunur g1 nM3M23 2 displaystyle g 1 frac sqrt n M 3 M 2 3 2 carpiklik g2 nM4M22 displaystyle g 2 frac nM 4 M 2 2 basiklik Kucuk artisli hallerde yani B x displaystyle B x bu soyle basitlestirilebilir d x m displaystyle delta x m m m dn 1 displaystyle m m frac delta n 1 M2 M2 d2nn 1 displaystyle M 2 M 2 frac delta 2 n n 1 M3 M3 d3n n 1 n 1 2 3dM2n 1 displaystyle M 3 M 3 frac delta 3 n n 1 n 1 2 frac 3 delta M 2 n 1 M4 M4 d4n n2 n 1 n 1 3 6d2M2 n 1 2 4dM3n 1 displaystyle M 4 M 4 frac delta 4 n n 2 n 1 n 1 3 frac 6 delta 2 M 2 n 1 2 frac 4 delta M 3 n 1 Burada dikkati ceken nokta d n 1 displaystyle delta n 1 degerini korumak suretiyle sadece tek bir bolme isleminin gerekli olmasi ve boylece cok az bir ekstra maliyetle daha yuksek istatistiksel olculer hesaplanabilmesidir OrnekKullanilan komputerde butun floating nokta operasyonlarinin IEEE 754 cifte hassiyetli aritmetik ile yapildigi varsayilsin Sonsuz buyuklukte bir anakutleden n 5 buyuklugunde bir orneklem olarak 4 7 13 16 dd veri seti elde edildigini dusunelim Bu orneklem icin orneklem ortalamasi 10 olur ve yanli olmayan anakutle varyans kestirimi 30dur Hem I naif Algoritma hem de II iki gecisli Algoritma bu degerleri dogru olarak hesaplamaktadirlar Simdi ornekleme olarak su veri setini alalim 108 4 displaystyle 10 8 4 108 7 displaystyle 10 8 7 108 13 displaystyle 10 8 13 108 16 displaystyle 10 8 16 dd Bu orneklemin de birinci orneklem gibi ayni varyans kestirimine sahip olmasi gerekir II Algoritma bu varyansi dogru olarak hesaplamaktadir Fakat I Algoritma sonuc olarak tam 30 yerine 29 333333333333332 sonucu verir Bu dakiklik kaybinin belki kabul edilebilir tolerans oldugu ve I Algoritma kullanilmasinin nispeten onemsiz bir hata dogurdugu soylenebilir Fakat bu I Algoritma hesaplamasinda cok onemli bir eksiklik ve hataya isaret etmektedir Bu sefer orneklem olarak sunu alalim 109 4 displaystyle 10 9 4 109 7 displaystyle 10 9 7 109 13 displaystyle 10 9 13 109 16 displaystyle 10 9 16 dd Yine II Algoritma dogru anakutle varyans kestirimi olarak 30 gosterir Ama I Algoritma kullanilinca elde edilen kestirim hesabi 170 66666666666666 olarak verilir Bu cok onemli ve yapilmamasi gereken bir hatadir cunku kavram olarak tanimlamayla varyans degerinin hicbir zaman negatif olmamasi gerekir Ayrica bakinizVaryansKaynakca Mehmet Guven GUNVER Prof Dr Mustafa Sukru SENOCAK Doc Dr Suphi VEHID Istatistikte Altin Oran Turkmen Kitabevi 2014 ISBN 9786054749409 Knuth D E 1998 The Art of Computer Programming V 2 Seminumerical Algorithms 3 ed p 232 Boston Addison Wesley Welford B P 1962 Note on a method for calculating corrected sums of squares and products Technometrics C 4 No 3 say 419 420 1 D H D West 1979 22 9 532 535 Updating Mean and Variance Estimates An Improved Method Terriberry T B 2007 Computing Higher Order Moments Online url http people xiph org tterribe notes homs html 23 Nisan 2014 tarihinde Wayback Machine sitesinde Dis baglantilarEric W Weisstein Sample Variance Computation MathWorld
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans