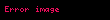Matematikte matris veya dizey, dikdörtgen bir sayılar tablosu veya daha genel bir açıklamayla, toplanabilir veya çarpılabilir soyut miktarlar tablosudur. Dizeyler daha çok doğrusal denklemleri tanımlamak, doğrusal dönüşümlerde (lineer transformasyon) çarpanların takibi ve iki parametreye bağlı verilerin kaydedilmesi amacıyla kullanılırlar. Dizeylerin toplanabilir, çıkartılabilir, çarpılabilir, bölünebilir ve ayrıştırılabilir olmaları, doğrusal cebir ve temel kavramı olmalarını sağlamıştır.

Bir diğer deyişle matris, doğal sayıları dikdörtgen halinde dizip gösteren bir tablodur. Örneğin:
Bir diğer notasyona göre dikdörtgen parantezler yerine eğri şekilli parantez kullanılır:
Bir matrisdeki düz yatay sıraya satır dikey sıraya sütun adı verilir. Bir matris içinde dizili gösterilen sayılar öğe veya eleman olarak adlandırılır. Matrisin büyüklüğü satır ve sütun sayılarıyla ifade edilir. Yukarıdaki matrisler 4x3 (yani 4 satırlı 3 sütunlu) matrislerdir.
Genel matematiksel notasyon olarak bir matris tek büyük harf ile ifade edilir. Bazen, daha açık olarak vurgulu kalın harf ile gösterilir. Bu vurgu bilgisayar ile yazılırsa kalın yazıyla; elle yazılırsa matris harfinin altına bir (bazen iki) çizgi veya küçük dalgalı bir çizgi koymak suretiyle yapılır. Farklı bir notasyon da matrisin parantez içinde küçük harfle ifade edilen genel elemanını i satır ve j sütun alt indisli ve parantez dışında matris büyüklüğü ile vermektir. Örneğin m satırlı n sütunlu mxn türünden bir A matrisi aşağıdaki şekillerde gösterilebilir:
- A veya
- veya
Böylece genel olarak m ve n pozitif tamsayılar, ve olmak üzere sayma sayılarından oluşan yukarıdaki sayılar tablosu matris (dizey) olur. m, matrisin satır sayısını; n ise matrisin sütun sayısını belirtir. m satır ve n sütundan oluşan matrise türünden matris denir:
Türleri
Kare matris
Satır sayısı sütun sayısına eşit olan matrislerdir. 
A dizeyi 2x2 türünden bir kare matrisdir.
Birim matris
Kare matrislerin yaygın bir örneği ise, köşegenin üzerindeki öğelerinin 1 geri kalan yerlerdeki öğelerin 0 olduğu birim matristir. Satır ve sütun sayısı n olan bir birim matrisi göstermek için (başka bir yerde kullanılmamışsa) genelde In kullanılır. Mesela, 3x3'lük bir birim matris

şeklinde gösterilir.
Sıfır matris
Tüm elemanları sıfır olan matrisdir. 
A dizeyi 2x3'lük bir sıfır matrisdir.
Satır ve sütun matris
Sadece bir satırdan oluşan matrislere satır matris, sadece bir sütundan oluşan matrislere ise sütun matris denir. 

Eğer bir matrisin boyutlarından biri 1 ise (yani ya satır sayısı 1 veya sütun sayısı 1 ise yani satır matrisi veya sütun matrisi ise) bu matris, bir yöney veya vektör veya Euclid-tipi vektör olarak da tanımlanır.
Cebirsel işlemler
Matrisler için sayıyla çarpma ve matris çarpımı farklı kavramlardır.
Matris toplaması
Matrisler bileşenleri karşılıklı olarak toplanırlar.
İki matrisin toplanabilmesi için satır ve sütün sayılarının eşit olması gerekir.
Örnek:
Sayıyla (Skalerle) çarpma
Bir matris, bir sayıyla çarpılırsa her bileşeni o sayıyla çarpılır.
Örnek:
Transpoz
mxn boyutlu bir 
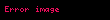

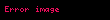

Matris çarpımı
Matris çarpımı ancak özel bir halde mümkündür ve genelde herhangi iki matris için matris çarpımı işlemi yapılamaz.
Çarpımı istenen iki matris için ilk önce matrislerden hangisinin ön-çarpan matris, hangisinin art-çarpan matris olduğunun belirlenmesi gerekir. Çünkü , sayılarda (değişmelidir), fakat matrislerde değildir. Yani genel olarak A ve B matrisi için A·B ≠ B·A
A·B matris çarpımı için A ön-çarpan ve B art-çarpan, B·A matris çarpımı için B ön-çarpan ve A art-çarpan olur. İki matris çarpımı notasyonla belirtilmekle beraber ya "A·B" ya "B·A" ya da hem "A·B" hem "B·A" geçerli olmayabilir.
Matris çarpımı ancak ön-çarpan sütun sayısı ile art-çarpan satır sayısı birbirine eşitse mümkündür. Yani (p * j) boyutlu A matrisi ile (k * l) boyutlu B matrisinin çarpımı ancak "j = k" ise mümkün olur; yoksa geçerli değildir. Eğer matris çarpımı geçerli ise, ortaya çıkartılacak çarpım matrisi, ön-çarpan satır sayısı ve art-çarpan matris sütun sayısı boyutludur Yani eğer "j = k" ise, matris çarpımı sonucu matrisi (p * l) boyutludur.
Sayısal bir örnek olarak, A matrisi (2 * 3) boyutlu ise ve B (3 * 4) boyutlu ise matris çarpımı (A·B), "j = k" (3 = 3) olduğu için geçerlidir ve matris çarpımı işlemi sonuç matrisi (2 * 4) boyutludur; ama B·A matris çarpımı işlemi geçerli değildir; çünkü "j ≠ k" (4 ≠ 2).

Matris çarpımının algoritması şu şekildedir: İlk öğenin i'nci satırının bileşenleriyle, ikinci öğenin j'nci sütununun bileşenleri karşılıklı olarak çarpılıp toplanır ve sonuç dizeyin bileşeni olarak yazılır.
- A, mxn boyutlu B de nxs boyutlu dizeyler olmak üzere mxs boyutlu sonuç dizey
- olarak tanımlanır ve her öğesi
ile bulunur.
Örnekler
Çarpmayı, ilk öğenin her satırını bir yöney ve ikinci öğenin her sütununu bir yöney olarak düşünüp ilk öğeyi bir ve ikinci öğeyi bir olarak yöney indirgeyebiliriz. Örneğin, 

ve
şeklinde düşünüldüğünde çarpım,
biçimini alır. Bu şekilde düşünmek kâğıt üzerinde dizeyleri çarparken işe yarayabilir ve zaman kazandırır.
Kronecker (Doğrudan) toplama
Bu toplamın sonucu bir matrisler köşegenidir.
- burada sonuç dizeyin boyutları, toplanan dizeylerin doğrudan boyutları toplamı kadardır.
Kronecker (Doğrudan) çarpım
Bu çarpım ilk öğenin her bileşenini ikinci öğeyle doğrudan çarpmayla tanımlanır.
- buradan,
Cebirsel ifade bir ya da birden fazla cebirsel terimin aynı ifade de yer almasına denir. Örneğin x sayısı gibi. Cebirsel ifadelerde en çok kullanılanlar: x,y,n dir. Cebirsel ifadelerle kurulmuş iki eşitliğe denklem denir. Mesela x+5=2x+2 çözüm bilenenler bir tarafa bilinmeyenler bir tarafa gönderilir. Öteki tarafa geçerken zıt işaret verilir yani: +5-2=2x-x sadeleştirirsek 3=x
Doğrusal denklemler sistemleri
Bir doğrusal denklem sistemi matrislerle ifade edilebilir.
Örnek olarak dört bilinmeyenli (x1, x2, x3 ve x4) dört tane doğrusal denklemler sistemi ele alınsın. Bu denklemlerdeki katsayılar, i denklem numarası ve j bilinmeyen numarası ile indislenerek ai,j olarak ifade edilebilir. Bu doğrusal denklemler sistemi şöyle yazılır:
Bu denklemler sistemi matris kullanılarak şöyle ifade edilir:
Daha kısa bir notasyonla şöyle yazılabilir:
Burada 
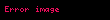



Genel olarak n sayıda değişkenli m sayıda doğrusal denklemden oluşan şu doğrusal denklemler sistemi:
- A1,1x1 + A1,2x2 + ... + A1,nxn = b1
- ...
- Am,1x1 + Am,2x2 + ... + Am,nxn = bm
çok kolayca bir denklemler matrisi olarak ifade edilebilir. Bunun için x yöneyi n değişken ('x1, x2, ..., xn) için bir n-sütun yöneyi (yani 'n×1-matrisi); A matrisi mxn boyutlu katsayılar matrisi ve b n-sutun yöneyi halindeki denklem sabitleri olursa, herhangi bir doğrusal denklem sistemi matris denklemi olarak şöyle ifade edilir:
- Ax = b.
Matematiksel matris kavramının tarihsel kaynağı
Doğrusal denklemler sistemlerinin çözülmesi için matris kavramlarının kullanılmasının çok uzun bir tarihi bulunmaktadır. Doğrusal denklemler sistemlerin ilk matris kullanarak açıklanıp çözülmesi, özellikle kare matrislerle ifade edilip determinant kullanımı dahil, MÖ.300 ile MS.200 arasında yazılmış olan Jiu Zhang Suan Shu (Matematik Sanatinda Dokuz Bölüm) adlı eserde bulunduğu anlaşılmıştır. Bu eserden Batı Avrupa matematikçileri hiç haberdar olmamışlardır. Bundan sonra matris kavramı 2000 yıl kadar sonra 1683'te "Seki Kowa" adlı Japon matematikçisi ve Batı Avrupa'da ilk defa 1693de Alman matematikçisi Leibniz tarafından ortaya atılmış ve ilk determinant kullanarak pratik çözüm olarak 1750'de tarafından gösterilmiştir.
Matris teorisinin Batı Avrupa'da geliştirilmesi daha çok determinant kavramına önem vermekteydi. Determinanttan bağımsız olarak matris matematiğinin geliştirilmesi 1858'de Arthur Cayley tarafından Memoir on the theory of matrices (Matris teorisi hakkında bir not) adında eserle başlamıştır. Matris terimi isim olarak ilk defa adlı İngiliz matematikçisi tarafından kullanılmıştır. Bu matematikçi determinantları açıp sayısal değerlerini bulmak için sütun ve satırları silip gittikçe daha küçük determinant (minor) elde ederek bu sonuca bulma üzerinde uğraşı göstermiş ve sanki bir ana determinanttan gittikçe küçülen "çocuk" determinantların bulunmasından ilham alarak şimdi matris olarak adlandırdığımız kavrama Latince kökten mater (anne) sözcüğünden çıkardığı matrix adını vermiştir.
Uygulamalar
Hem matematikte hem de diğer bilimlerde matrislerin çok sayıda uygulaması vardır. Bazıları yalnızca bir matristeki bir dizi sayının kompakt temsilinden yararlanır. Örneğin, oyun teorisi ve ekonomi'de ödeme matrisi, oyuncuların belirli (sonlu) alternatifler arasından hangisini seçtiğine bağlı olarak iki oyuncu için getiriyi kodlar.Metin madenciliği ve otomatikleştirilmiş Tesarus derlemesi, çeşitli belgelerdeki belirli kelimelerin sıklıklarını izlemek için örneğin tf-idf gibi belge-terim matrislerini kullanır.
Karmaşık sayılar, karmaşık sayıların ve matrislerin toplanması ve çarpılmasının birbirine karşılık geldiği
aracılığıyla belirli gerçek 2'ye 2 matrislerle temsil edilebilir.
Örneğin 2'ye 2 döndürme matrisleri, yukarıda gibi bazı mutlak değer 1 karmaşık sayısıyla çarpmayı gösterir. Genel olarak dördeyler ve Clifford cebirleri için de benzer bir yorum mümkündür.
Hill cipher gibi eski şifreleme teknikleri de matrisleri kullandı. Ancak matrislerin doğrusal doğası nedeniyle bu kodların kırılması nispeten kolaydır.
Bilgisayar grafikleri teorik kamera gözlemine karşılık gelen, üç boyutlu bir nesneyi iki boyutlu bir ekrana yansıtmak gibi görevleri gerçekleştirmede afin dönüş matrislerini kullanarak nesnelerin dönüşümlerini hesaplamada ve keskinleştirme, bulanıklaştırma, kenar algılama vb görüntü kıvrımlarını uygulamada nesneleri temsil için matrisleri kullanır.Polinom halkası üzerindeki matrisler, kontrol teorisi çalışmasında önemlidir.
Kimya'da özellikle kuantum teorisi moleküler bağı ve spektroskopiyi anlatmak için kullanıldığından beri matrisler çeşitli şekillerde kullanılmaktadır. Hartree–Fock yönteminin moleküler orbital'lerini elde etmek için Roothaan denklemlerini çözmek için kullanılan örtüşme matrisi ve Fock matrisi kimyadaki bazı kullanım örnekleridir.
Grafik teorisi


Bir sonlu grafiğin bitişik matrisi, grafik teorisi'nin temel kavramıdır. Grafiğin hangi köşelerinin bir kenarla bağlandığını kaydeder. Yalnızca iki farklı değer içeren matrislere (1 ve 0 sırasıyla "evet" ve "hayır" anlamına gelir) mantıksal matrisler denir.
Mesafe matrisi kenarların mesafeleri hakkında bilgi içerir. Bu kavramlar, hiperlinkler ile bağlanan web sitelerine veya karayolu vb. ile bağlanan şehirlere uygulanabilir bu durumda (bağlantı ağı aşırı derecede yoğun olmadığı sürece) matrisler seyrek olma eğilimindedir yani sıfır olmayan birkaç giriş içerir. Bu nedenle özel uyarlanmış matris algoritmaları ağ teorisinde kullanılabilir.
Analiz ve Geometri
Türevlenebilir bir ƒ fonksiyonunun Hesse matrisi: Rn → R, ƒ 'nin birkaç koordinat yönüne göre ikinci türevlerinden oluşur yani,

 belirsizdir.
belirsizdir.Fonksiyonun yerel büyüme davranışı hakkındaki bilgileri kodlar: x = (x1, ..., xn), kritik noktası verildiğinde, yani ƒ'in birinci kısmi türevlerinin 
Geometrik durumlarda sıklıkla kullanılan başka bir matris, Rn → Rm türevlenebilir bir haritanın Jacobi matrisidir. Eğer f1, ..., fm, f'nin bileşenlerini gösteriyorsa, Jacobi matrisi şu şekilde tanımlanır
n > m ise ve Jacobi matrisinin rankı maksimum değeri mye ulaşıyorsa, f bu noktada örtük fonksiyon teoremi ile yerel olarak tersinebilir.
Kısmi diferansiyel denklemler, denklemin en yüksek mertebeden diferansiyel operatörlerinin katsayı matrisi dikkate alınarak sınıflandırılabilir. Eliptik kısmi diferansiyel denklemler için bu matris pozitif tanımlıdır ve söz konusu denklemin olası çözüm kümesi üzerinde belirleyici bir etkiye sahiptir.
Sonlu elemanlar yöntemi, karmaşık fiziksel sistemleri simüle etmede yaygın olarak uygulanan, kısmi diferansiyel denklemleri çözmek için önemli bir sayısal yöntemdir. Parçaların yeterince ince bir ızgaraya göre seçildiği ve bunun da bir matris denklemi olarak yeniden şekillendirilebildiği parçalı lineer fonksiyonlarla bazı denklemlerin çözümüne yaklaşmaya çalışır.
Kaynakça
- ^ Fudenberg & Tirole 1983, Section 1.1.1
- ^ Manning 1999, Section 15.3.4
- ^ Ward 1997, Ch. 2.8
- ^ Stinson 2005, Ch. 1.1.5 and 1.2.4
- ^ Association for Computing Machinery 1979, Ch. 7
- ^ Godsil & Royle 2004, Ch. 8.1
- ^ Punnen 2002
- ^ Lang 1987a, Ch. XVI.6
- ^ Nocedal 2006, Ch. 16
- ^ Lang 1987a, Ch. XVI.1
- ^ Lang 1987a, Ch. XVI.5. For a more advanced, and more general statement see Lang 1969, Ch. VI.2
- ^ Gilbarg & Trudinger 2001
- ^ Šolin 2005, Ch. 2.5. Ayrıca bkz; .
Dış bağlantılar
- İngilizce Wikipedia "Matrix (mathematics)" maddesi:[1]10 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce) (Erişme:15.3.2010)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte matris veya dizey dikdortgen bir sayilar tablosu veya daha genel bir aciklamayla toplanabilir veya carpilabilir soyut miktarlar tablosudur Dizeyler daha cok dogrusal denklemleri tanimlamak dogrusal donusumlerde lineer transformasyon carpanlarin takibi ve iki parametreye bagli verilerin kaydedilmesi amaciyla kullanilirlar Dizeylerin toplanabilir cikartilabilir carpilabilir bolunebilir ve ayristirilabilir olmalari dogrusal cebir ve temel kavrami olmalarini saglamistir Bir matrisin dizilisi m satirlari n sutunlari temsil eder Bir diger deyisle matris dogal sayilari dikdortgen halinde dizip gosteren bir tablodur Ornegin A 128316212217149201605 displaystyle mathbf A begin bmatrix 12 amp 83 amp 16 21 amp 22 amp 17 14 amp 9 amp 20 16 amp 0 amp 5 end bmatrix Bir diger notasyona gore dikdortgen parantezler yerine egri sekilli parantez kullanilir A 986127492605 displaystyle mathbf A begin pmatrix 9 amp 8 amp 6 1 amp 2 amp 7 4 amp 9 amp 2 6 amp 0 amp 5 end pmatrix Bir matrisdeki duz yatay siraya satir dikey siraya sutun adi verilir Bir matris icinde dizili gosterilen sayilar oge veya eleman olarak adlandirilir Matrisin buyuklugu satir ve sutun sayilariyla ifade edilir Yukaridaki matrisler 4x3 yani 4 satirli 3 sutunlu matrislerdir Genel matematiksel notasyon olarak bir matris tek buyuk harf ile ifade edilir Bazen daha acik olarak vurgulu kalin harf ile gosterilir Bu vurgu bilgisayar ile yazilirsa kalin yaziyla elle yazilirsa matris harfinin altina bir bazen iki cizgi veya kucuk dalgali bir cizgi koymak suretiyle yapilir Farkli bir notasyon da matrisin parantez icinde kucuk harfle ifade edilen genel elemanini i satir ve j sutun alt indisli ve parantez disinda matris buyuklugu ile vermektir Ornegin m satirli n sutunlu mxn turunden bir A matrisi asagidaki sekillerde gosterilebilir A veya A displaystyle underline underline A veya A aij mxn displaystyle A a ij mxn Boylece genel olarak m ve n pozitif tamsayilar i 1 2 3 4 m displaystyle i in 1 2 3 4 cdots m ve j 1 2 3 4 n displaystyle j in 1 2 3 4 cdots n olmak uzere ai j displaystyle a i j sayma sayilarindan olusan yukaridaki sayilar tablosu matris dizey olur m matrisin satir sayisini n ise matrisin sutun sayisini belirtir m satir ve n sutundan olusan matrise mxn displaystyle mxn turunden matris denir A Am n a1 1a1 2 a1 na2 1a2 2 a2 n am 1am 2 am n displaystyle mathbf A A m n begin bmatrix a 1 1 amp a 1 2 amp cdots amp a 1 n a 2 1 amp a 2 2 amp cdots amp a 2 n vdots amp vdots amp ddots amp vdots a m 1 amp a m 2 amp cdots amp a m n end bmatrix TurleriKare matris Satir sayisi sutun sayisina esit olan matrislerdir A2 2 2 105 displaystyle A 2 2 begin bmatrix 2 amp 1 0 amp 5 end bmatrix A dizeyi 2x2 turunden bir kare matrisdir Birim matris Kare matrislerin yaygin bir ornegi ise kosegenin uzerindeki ogelerinin 1 geri kalan yerlerdeki ogelerin 0 oldugu birim matristir Satir ve sutun sayisi n olan bir birim matrisi gostermek icin baska bir yerde kullanilmamissa genelde In kullanilir Mesela 3x3 luk bir birim matris I3 100010001 displaystyle I 3 begin bmatrix 1 amp 0 amp 0 0 amp 1 amp 0 0 amp 0 amp 1 end bmatrix seklinde gosterilir Sifir matris Tum elemanlari sifir olan matrisdir A2 3 000000 displaystyle A 2 3 begin bmatrix 0 amp 0 amp 0 0 amp 0 amp 0 end bmatrix A dizeyi 2x3 luk bir sifir matrisdir Satir ve sutun matris Sadece bir satirdan olusan matrislere satir matris sadece bir sutundan olusan matrislere ise sutun matris denir Am n 000 displaystyle A m n begin bmatrix 0 amp 0 amp 0 end bmatrix Bm n 000 displaystyle B m n begin bmatrix 0 0 0 end bmatrix Eger bir matrisin boyutlarindan biri 1 ise yani ya satir sayisi 1 veya sutun sayisi 1 ise yani satir matrisi veya sutun matrisi ise bu matris bir yoney veya vektor veya Euclid tipi vektor olarak da tanimlanir Cebirsel islemlerMatrisler icin sayiyla carpma ve matris carpimi farkli kavramlardir Matris toplamasi Matrisler bilesenleri karsilikli olarak toplanirlar Iki matrisin toplanabilmesi icin satir ve sutun sayilarinin esit olmasi gerekir C A B cij aij bij displaystyle mathbf C mathbf A mathbf B implies c ij a ij b ij Ornek 132100122 005750211 1 03 02 51 70 50 01 22 12 1 137850333 displaystyle begin bmatrix 1 amp 3 amp 2 1 amp 0 amp 0 1 amp 2 amp 2 end bmatrix begin bmatrix 0 amp 0 amp 5 7 amp 5 amp 0 2 amp 1 amp 1 end bmatrix begin bmatrix 1 0 amp 3 0 amp 2 5 1 7 amp 0 5 amp 0 0 1 2 amp 2 1 amp 2 1 end bmatrix begin bmatrix 1 amp 3 amp 7 8 amp 5 amp 0 3 amp 3 amp 3 end bmatrix Sayiyla Skalerle carpma Bir matris bir sayiyla carpilirsa her bileseni o sayiyla carpilir cij kaij displaystyle c ij ka ij dd Ornek 2 18 34 25 2 12 82 32 42 22 5 216 68 410 displaystyle 2 begin bmatrix 1 amp 8 amp 3 4 amp 2 amp 5 end bmatrix begin bmatrix 2 times 1 amp 2 times 8 amp 2 times 3 2 times 4 amp 2 times 2 amp 2 times 5 end bmatrix begin bmatrix 2 amp 16 amp 6 8 amp 4 amp 10 end bmatrix Transpoz mxn boyutlu bir A displaystyle A matrisinin transpozu nxm boyutlu AT displaystyle A T matrisidir 1230 67 T 102 637 displaystyle begin bmatrix 1 amp 2 amp 3 0 amp 6 amp 7 end bmatrix mathrm T begin bmatrix 1 amp 0 2 amp 6 3 amp 7 end bmatrix AT displaystyle A T matrisi A displaystyle A nin satirlarini sutun yaparak elde edilir Transpoz islemi matrisin ifade ettigi donusumun yonunu tersine cevirir Matris carpimi Matris carpimi ancak ozel bir halde mumkundur ve genelde herhangi iki matris icin matris carpimi islemi yapilamaz Carpimi istenen iki matris icin ilk once matrislerden hangisinin on carpan matris hangisinin art carpan matris oldugunun belirlenmesi gerekir Cunku sayilarda degismelidir fakat matrislerde degildir Yani genel olarak A ve B matrisi icin A B B A A B matris carpimi icin A on carpan ve B art carpan B A matris carpimi icin B on carpan ve A art carpan olur Iki matris carpimi notasyonla belirtilmekle beraber ya A B ya B A ya da hem A B hem B A gecerli olmayabilir Matris carpimi ancak on carpan sutun sayisi ile art carpan satir sayisi birbirine esitse mumkundur Yani p j boyutlu A matrisi ile k l boyutlu B matrisinin carpimi ancak j k ise mumkun olur yoksa gecerli degildir Eger matris carpimi gecerli ise ortaya cikartilacak carpim matrisi on carpan satir sayisi ve art carpan matris sutun sayisi boyutludur Yani eger j k ise matris carpimi sonucu matrisi p l boyutludur Sayisal bir ornek olarak A matrisi 2 3 boyutlu ise ve B 3 4 boyutlu ise matris carpimi A B j k 3 3 oldugu icin gecerlidir ve matris carpimi islemi sonuc matrisi 2 4 boyutludur ama B A matris carpimi islemi gecerli degildir cunku j k 4 2 A ve B matrislerinin matris carpimi A B ifadesinin bir sema ile gosterimi Matris carpiminin algoritmasi su sekildedir Ilk ogenin i nci satirinin bilesenleriyle ikinci ogenin j nci sutununun bilesenleri karsilikli olarak carpilip toplanir ve sonuc dizeyin bileseni olarak yazilir A mxn boyutlu B de nxs boyutlu dizeyler olmak uzere mxs boyutlu sonuc dizeyAm nBn s Cm s displaystyle A m times n B n times s C m times s dd olarak tanimlanir ve her ogesicij k 1naikbkj displaystyle c ij sum k 1 n a ik b kj dd ile bulunur Ornekler 102 131 312110 1 3 0 2 2 1 1 1 0 1 2 0 1 3 3 2 1 1 1 1 3 1 1 0 5142 displaystyle begin bmatrix 1 amp 0 amp 2 1 amp 3 amp 1 end bmatrix begin bmatrix 3 amp 1 2 amp 1 1 amp 0 end bmatrix begin bmatrix 1 times 3 0 times 2 2 times 1 amp 1 times 1 0 times 1 2 times 0 1 times 3 3 times 2 1 times 1 amp 1 times 1 3 times 1 1 times 0 end bmatrix begin bmatrix 5 amp 1 4 amp 2 end bmatrix Carpmayi ilk ogenin her satirini bir yoney ve ikinci ogenin her sutununu bir yoney olarak dusunup ilk ogeyi bir ve ikinci ogeyi bir olarak yoney indirgeyebiliriz Ornegin a displaystyle vec a ve b displaystyle vec b yoneyleri n boyutlu olmak uzere Am n a1 am displaystyle A m times n begin bmatrix vec a 1 cdots vec a m end bmatrix ve Bn s b1 bs displaystyle B n times s begin bmatrix vec b 1 amp amp cdots amp amp vec b s end bmatrix seklinde dusunuldugunde carpim AB a1 b1 a1 bs am b1 am bs displaystyle AB begin bmatrix vec a 1 cdot vec b 1 amp amp cdots amp amp vec a 1 cdot vec b s vdots amp amp ddots amp amp ddots vec a m cdot vec b 1 amp amp cdots amp amp vec a m cdot vec b s end bmatrix bicimini alir Bu sekilde dusunmek kagit uzerinde dizeyleri carparken ise yarayabilir ve zaman kazandirir 30 12 7 136 displaystyle begin bmatrix 3 amp 0 1 amp 2 end bmatrix begin bmatrix 7 amp 1 3 amp 6 end bmatrix 3 0 1 2 7 3 1 6 displaystyle begin bmatrix 3 0 1 2 end bmatrix begin bmatrix 7 3 amp 1 6 end bmatrix 3 0 7 3 3 0 1 6 1 2 7 3 1 2 1 6 21 3 113 displaystyle begin bmatrix 3 0 cdot 7 3 amp amp 3 0 cdot 1 6 1 2 cdot 7 3 amp amp 1 2 cdot 1 6 end bmatrix begin bmatrix 21 amp amp 3 1 amp amp 13 end bmatrix Kronecker Dogrudan toplama Bu toplamin sonucu bir matrisler kosegenidir C i 1kAi kosegen A1 A2 Ak A10 00A2 0 00 Ak displaystyle C oplus i 1 k A i text kosegen left A 1 A 2 A k right left begin array cccc A 1 amp 0 amp cdots amp 0 0 amp A 2 amp cdots amp 0 vdots amp vdots amp ddots amp vdots 0 amp 0 amp cdots amp A k end array right dd burada sonuc dizeyin boyutlari toplanan dizeylerin dogrudan boyutlari toplami kadardir Kronecker Dogrudan carpim Bu carpim ilk ogenin her bilesenini ikinci ogeyle dogrudan carpmayla tanimlanir Am n Br s a11Ba12B a1nBa21Ba22B a2nB am1Bam2B amnB displaystyle A m times n otimes B r times s left begin array cccc a 11 B amp a 12 B amp cdots amp a 1n B a 21 B amp a 22 B amp cdots amp a 2n B vdots amp vdots amp ddots amp vdots a m1 B amp a m2 B amp cdots amp a mn B end array right dd buradan C mr ns a11b11a11b12 a12b11 a11b21a11b22 a12b21 a21b11a21b12 displaystyle C mr times ns left begin array ccccc a 11 b 11 amp a 11 b 12 amp cdots amp a 12 b 11 amp cdots a 11 b 21 amp a 11 b 22 amp cdots amp a 12 b 21 amp cdots vdots amp vdots amp ddots amp quad amp quad a 21 b 11 amp a 21 b 12 amp quad amp ddots amp quad vdots amp vdots amp quad amp quad amp ddots end array right dd Cebirsel ifade bir ya da birden fazla cebirsel terimin ayni ifade de yer almasina denir Ornegin x sayisi gibi Cebirsel ifadelerde en cok kullanilanlar x y n dir Cebirsel ifadelerle kurulmus iki esitlige denklem denir Mesela x 5 2x 2 cozum bilenenler bir tarafa bilinmeyenler bir tarafa gonderilir Oteki tarafa gecerken zit isaret verilir yani 5 2 2x x sadelestirirsek 3 xDogrusal denklemler sistemleriBir dogrusal denklem sistemi matrislerle ifade edilebilir Ornek olarak dort bilinmeyenli x1 x2 x3 ve x4 dort tane dogrusal denklemler sistemi ele alinsin Bu denklemlerdeki katsayilar i denklem numarasi ve j bilinmeyen numarasi ile indislenerek ai j olarak ifade edilebilir Bu dogrusal denklemler sistemi soyle yazilir a11x1 a12x2 a13x3 a14x4 b1a21x1 a22x2 a23x3 a24x4 b2a31x1 a32x2 a33x3 a34x4 b3a41x1 a42x2 a43x3 a44x4 b4 displaystyle begin aligned a 11 x 1 a 12 x 2 a 13 x 3 a 14 x 4 amp b 1 a 21 x 1 a 22 x 2 a 23 x 3 a 24 x 4 amp b 2 a 31 x 1 a 32 x 2 a 33 x 3 a 34 x 4 amp b 3 a 41 x 1 a 42 x 2 a 43 x 3 a 44 x 4 amp b 4 end aligned Bu denklemler sistemi matris kullanilarak soyle ifade edilir a11a12a13a14a21a22a23a24a31a32a33a34a41a42a43a44 x1x2x3x4 b1b2b3b4 displaystyle begin bmatrix a 11 amp a 12 amp a 13 amp a 14 a 21 amp a 22 amp a 23 amp a 24 a 31 amp a 32 amp a 33 amp a 34 a 41 amp a 42 amp a 43 amp a 44 end bmatrix begin bmatrix x 1 x 2 x 3 x 4 end bmatrix begin bmatrix b 1 b 2 b 3 b 4 end bmatrix Daha kisa bir notasyonla soyle yazilabilir A x b veya Ax b displaystyle left mathsf A right left mathsf x right left mathsf b right text veya mathbf A mathbf x mathbf b Burada A displaystyle mathbf A 4 4 displaystyle 4 times 4 boyutlu matrisdir x displaystyle mathbf x ve b displaystyle mathbf b 4 1 displaystyle 4 times 1 boyutlu sutun matrislerdir Genel olarak n sayida degiskenli m sayida dogrusal denklemden olusan su dogrusal denklemler sistemi A1 1x1 A1 2x2 A1 nxn b1 Am 1x1 Am 2x2 Am nxn bm cok kolayca bir denklemler matrisi olarak ifade edilebilir Bunun icin x yoneyi n degisken x1 x2 xn icin bir n sutun yoneyi yani n 1 matrisi A matrisi mxn boyutlu katsayilar matrisi ve b n sutun yoneyi halindeki denklem sabitleri olursa herhangi bir dogrusal denklem sistemi matris denklemi olarak soyle ifade edilir Ax b Matematiksel matris kavraminin tarihsel kaynagiDogrusal denklemler sistemlerinin cozulmesi icin matris kavramlarinin kullanilmasinin cok uzun bir tarihi bulunmaktadir Dogrusal denklemler sistemlerin ilk matris kullanarak aciklanip cozulmesi ozellikle kare matrislerle ifade edilip determinant kullanimi dahil MO 300 ile MS 200 arasinda yazilmis olan Jiu Zhang Suan Shu Matematik Sanatinda Dokuz Bolum adli eserde bulundugu anlasilmistir Bu eserden Bati Avrupa matematikcileri hic haberdar olmamislardir Bundan sonra matris kavrami 2000 yil kadar sonra 1683 te Seki Kowa adli Japon matematikcisi ve Bati Avrupa da ilk defa 1693de Alman matematikcisi Leibniz tarafindan ortaya atilmis ve ilk determinant kullanarak pratik cozum olarak 1750 de tarafindan gosterilmistir Matris teorisinin Bati Avrupa da gelistirilmesi daha cok determinant kavramina onem vermekteydi Determinanttan bagimsiz olarak matris matematiginin gelistirilmesi 1858 de Arthur Cayley tarafindan Memoir on the theory of matrices Matris teorisi hakkinda bir not adinda eserle baslamistir Matris terimi isim olarak ilk defa adli Ingiliz matematikcisi tarafindan kullanilmistir Bu matematikci determinantlari acip sayisal degerlerini bulmak icin sutun ve satirlari silip gittikce daha kucuk determinant minor elde ederek bu sonuca bulma uzerinde ugrasi gostermis ve sanki bir ana determinanttan gittikce kuculen cocuk determinantlarin bulunmasindan ilham alarak simdi matris olarak adlandirdigimiz kavrama Latince kokten mater anne sozcugunden cikardigi matrix adini vermistir UygulamalarHem matematikte hem de diger bilimlerde matrislerin cok sayida uygulamasi vardir Bazilari yalnizca bir matristeki bir dizi sayinin kompakt temsilinden yararlanir Ornegin oyun teorisi ve ekonomi de odeme matrisi oyuncularin belirli sonlu alternatifler arasindan hangisini sectigine bagli olarak iki oyuncu icin getiriyi kodlar Metin madenciligi ve otomatiklestirilmis Tesarus derlemesi cesitli belgelerdeki belirli kelimelerin sikliklarini izlemek icin ornegin tf idf gibi belge terim matrislerini kullanir Karmasik sayilar karmasik sayilarin ve matrislerin toplanmasi ve carpilmasinin birbirine karsilik geldigi a ib a bba displaystyle a ib leftrightarrow begin bmatrix a amp b b amp a end bmatrix araciligiyla belirli gercek 2 ye 2 matrislerle temsil edilebilir Ornegin 2 ye 2 dondurme matrisleri yukarida gibi bazi mutlak deger 1 karmasik sayisiyla carpmayi gosterir Genel olarak dordeyler ve Clifford cebirleri icin de benzer bir yorum mumkundur Hill cipher gibi eski sifreleme teknikleri de matrisleri kullandi Ancak matrislerin dogrusal dogasi nedeniyle bu kodlarin kirilmasi nispeten kolaydir Bilgisayar grafikleri teorik kamera gozlemine karsilik gelen uc boyutlu bir nesneyi iki boyutlu bir ekrana yansitmak gibi gorevleri gerceklestirmede afin donus matrislerini kullanarak nesnelerin donusumlerini hesaplamada ve keskinlestirme bulaniklastirma kenar algilama vb goruntu kivrimlarini uygulamada nesneleri temsil icin matrisleri kullanir Polinom halkasi uzerindeki matrisler kontrol teorisi calismasinda onemlidir Kimya da ozellikle kuantum teorisi molekuler bagi ve spektroskopiyi anlatmak icin kullanildigindan beri matrisler cesitli sekillerde kullanilmaktadir Hartree Fock yonteminin molekuler orbital lerini elde etmek icin Roothaan denklemlerini cozmek icin kullanilan ortusme matrisi ve Fock matrisi kimyadaki bazi kullanim ornekleridir Grafik teorisi Yakinlik matrisine sahip yonsuz bir grafik 110101010 displaystyle begin bmatrix 1 amp 1 amp 0 1 amp 0 amp 1 0 amp 1 amp 0 end bmatrix Bir sonlu grafigin bitisik matrisi grafik teorisi nin temel kavramidir Grafigin hangi koselerinin bir kenarla baglandigini kaydeder Yalnizca iki farkli deger iceren matrislere 1 ve 0 sirasiyla evet ve hayir anlamina gelir mantiksal matrisler denir Mesafe matrisi kenarlarin mesafeleri hakkinda bilgi icerir Bu kavramlar hiperlinkler ile baglanan web sitelerine veya karayolu vb ile baglanan sehirlere uygulanabilir bu durumda baglanti agi asiri derecede yogun olmadigi surece matrisler seyrek olma egilimindedir yani sifir olmayan birkac giris icerir Bu nedenle ozel uyarlanmis matris algoritmalari ag teorisinde kullanilabilir Analiz ve Geometri Turevlenebilir bir ƒ fonksiyonunun Hesse matrisi Rn R ƒ nin birkac koordinat yonune gore ikinci turevlerinden olusur yani H f 2f xi xj displaystyle H f left frac partial 2 f partial x i partial x j right x 0 y 0 eyer noktasinda kirmizi f x y fonksiyonunun x2 y 2 Hessen matrisi 200 2 displaystyle begin bmatrix 2 amp 0 0 amp 2 end bmatrix belirsizdir Fonksiyonun yerel buyume davranisi hakkindaki bilgileri kodlar x x1 xn kritik noktasi verildiginde yani ƒ in birinci kismi turevlerinin f xi displaystyle partial f partial x i sifir oldugu noktada Hesse matrisi pozitif tanimliysa fonksiyonun yerel bir minimumu vardir Ikinci dereceden programlama matrislere bagli olanlarla yakindan iliskili ikinci dereceden fonksiyonlarin global minimum veya maksimumlarini bulmak icin kullanilabilir bkz yukarida Geometrik durumlarda siklikla kullanilan baska bir matris Rn Rm turevlenebilir bir haritanin Jacobi matrisidir Eger f1 fm f nin bilesenlerini gosteriyorsa Jacobi matrisi su sekilde tanimlanir J f fi xj 1 i m 1 j n displaystyle J f left frac partial f i partial x j right 1 leq i leq m 1 leq j leq n n gt m ise ve Jacobi matrisinin ranki maksimum degeri mye ulasiyorsa f bu noktada ortuk fonksiyon teoremi ile yerel olarak tersinebilir Kismi diferansiyel denklemler denklemin en yuksek mertebeden diferansiyel operatorlerinin katsayi matrisi dikkate alinarak siniflandirilabilir Eliptik kismi diferansiyel denklemler icin bu matris pozitif tanimlidir ve soz konusu denklemin olasi cozum kumesi uzerinde belirleyici bir etkiye sahiptir Sonlu elemanlar yontemi karmasik fiziksel sistemleri simule etmede yaygin olarak uygulanan kismi diferansiyel denklemleri cozmek icin onemli bir sayisal yontemdir Parcalarin yeterince ince bir izgaraya gore secildigi ve bunun da bir matris denklemi olarak yeniden sekillendirilebildigi parcali lineer fonksiyonlarla bazi denklemlerin cozumune yaklasmaya calisir Kaynakca Fudenberg amp Tirole 1983 Section 1 1 1 Manning 1999 Section 15 3 4 Ward 1997 Ch 2 8 Stinson 2005 Ch 1 1 5 and 1 2 4 Association for Computing Machinery 1979 Ch 7 Godsil amp Royle 2004 Ch 8 1 Punnen 2002 Lang 1987a Ch XVI 6 Nocedal 2006 Ch 16 Lang 1987a Ch XVI 1 Lang 1987a Ch XVI 5 For a more advanced and more general statement see Lang 1969 Ch VI 2 Gilbarg amp Trudinger 2001 Solin 2005 Ch 2 5 Ayrica bkz Dis baglantilarIngilizce Wikipedia Matrix mathematics maddesi 1 10 Subat 2010 tarihinde Wayback Machine sitesinde arsivlendi Ingilizce Erisme 15 3 2010
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans


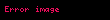
![{\displaystyle \ A=[a_{ij}]_{mxn}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aVpUVXdOVGt6TW1Zd1lUZGhNRGcxWlRkbE1qSmpOVGhtWW1ZeFlXRm1ZelJqTUdRNE9XTmguc3Zn.svg)