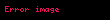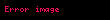Azərbaycanca AzərbaycancaБеларускі БеларускіDansk DanskDeutsch DeutschEspañola EspañolaFrançais FrançaisIndonesia IndonesiaItaliana Italiana日本語 日本語Қазақ ҚазақLietuvos LietuvosNederlands NederlandsPortuguês PortuguêsРусский Русскийසිංහල සිංහලแบบไทย แบบไทยTürkçe TürkçeУкраїнська Українська中國人 中國人United State United StateAfrikaans Afrikaans
Destek
www.wikipedia.tr-tr.nina.az
  • Vikipedi

Matematik fizik ve mühendislikte öklid vektörü veya kısaca vektör bazen geometrik vektör konumsal vektör ya da y

Vektörler

Vektörler
www.wikipedia.tr-tr.nina.azhttps://www.wikipedia.tr-tr.nina.az

Matematik, fizik ve mühendislikte, Öklid vektörü veya kısaca vektör (bazen geometrik vektör,konumsal vektör ya da yöney) sayısal büyüklüğü (veya uzunluğu) ve yönü olan geometrik bir objedir. Vektör, genellikle bir doğru parçası ile özdeşleştirilir. Bir başlangıç noktası A ile bir uç noktası B'yi birleştiren bir ok şeklinde görselleştirilir ve AB→{\displaystyle {\overrightarrow {AB}}}{\displaystyle {\overrightarrow {AB}}} ile belirtilir.

image
A noktasından B noktasına çizili bir vektör.

Hız, kuvvet, ivme ve ağırlık örnek birer vektörel niceliktir. Vektörler bir sayı (skaler) ile veya başka bir vektör ile çarpılabilir ve bölünebilir. Aynı zamanda yönü değiştirilmemek şartı ile ötelenebilirler. Vektörlerin yönlü doğru parçalarından farkı budur. Yönlü doğru parçalarının koordinat sistemindeki yeri sabitken, vektörler ötelenebilirler.

Köken

İngilizcede bu yapı için kullanılan sözcük vector dür. Kökeni, "taşımak"/"bir yöne aktarmak"/"göndermek" anlamına gelen "vehere" Latince fiil gövdesidir. Sözcüğün anlamı "taşıyıcı"/"yöncü" olarak düşünülebilir. Bu yüzden olabilir ki Türkçede (büyük ihtimalle Fransızcadan devşirilmiş olan) vektör karşılığından sonra yöney karşılığı kullanılmaktadır.

Gösterimi

image
A noktasından B noktasına varan bir vektör oku

Fiziksel vektörler veya geometrik vektörler,iki boyutlu düzlem için tanımı şu şekilde yapılabilir. İki boyutlu düzlemde 2 tane nokta alınsın bu noktalar A ve B noktaları olsun. A noktasından(başlangıç noktası) B noktasına (bitiş noktası) çizilen ve normu olan bu yönlü doğru parçasına A'dan B'ye çizilen AB vektörü denir.

Gösterimi iki şekildedir : 1.gösterim AB→{\displaystyle {\overrightarrow {\mathrm {A} \mathrm {B} }}}{\displaystyle {\overrightarrow {\mathrm {A} \mathrm {B} }}}

2.gösterim AB

ile gösterilir.

Ok vektörün yönünü gösterir. Doğru parçasının uzunluğu ise, vektör büyüklüğü ile doğru orantılıdır.

image

İki boyutlu bir ; bazen bir vektör koordinat düzlemine dik olarak gösterilmesi gerekebilir. Bir dairenin merkezinde bir nokta bulunursa (⊙), bu sembol yönü gözlemciye doğru olan bir vektörü göstermektedir. Bir dairenin içinde bir çarpı işareti bulunursa (⊗), bu sembol yönü düzlemin arkasına doğru olan bir vektörü göstermektedir. Bu semboller, bir savaş okunun ucunun görüntülenmesi ve bir savaş okunun arka kanatlarının görüntülenmesi gibi düşünülebilir.

Bir vektörün büyüklüğü

Bir vektörün büyüklüğü başlangıç ve bitiş noktaları arasında kalan doğru parçasının uzunluğudur vektörler referans noktasına göre - ve+ olmak üzere iki yöne ayrılabilirler .- yönündeki vektöre negatif yönlü vektör,+yönündeki vektere pozitif yönlü vektör denir. Vektörlerin büyüklükleri skaler nicelik ifade eder o denli bu - ve + işaretlerinin skaler bir gösterimden uzaklaşması için vektörün mutlak değerini almamız gerekir.⟨e.a⟩

AB vektörünün normu |AB| dir .

Daha genel gösterim |AB→{\displaystyle {\overrightarrow {\mathrm {A} \mathrm {B} }}}{\displaystyle {\overrightarrow {\mathrm {A} \mathrm {B} }}}| dir.

Soyut tanımı

Soyut olarak vektörler, bir F cisminin üzerine tanımlı bir vektör uzayının ögeleridir. Vektörler bu cisim üzerine tanımlanmış bir denklik bağıntısı yardımıyla tanımlanabilir. a,b,c,d∈Fn=F×F×⋯×F{\displaystyle a,b,c,d\in F^{n}=F\times F\times \cdots \times F}{\displaystyle a,b,c,d\in F^{n}=F\times F\times \cdots \times F} (n tane) olsun. a ögesi ile b ögesi,ancak bileşenlerin toplamı olarak a+d=b+c ise bağıntılıdır. Daha biçimsel olmak gerekirse

a∼b⇔∀i∈{1,2,⋯,n}:ai+di=bi+ci{\displaystyle a\sim b\Leftrightarrow \forall i\in \{1,2,\cdots ,n\}:\quad a_{i}+d_{i}=b_{i}+c_{i}}{\displaystyle a\sim b\Leftrightarrow \forall i\in \{1,2,\cdots ,n\}:\quad a_{i}+d_{i}=b_{i}+c_{i}}

şeklinde tanımlanır ki burada ai∈F{\displaystyle a_{i}\in F}{\displaystyle a_{i}\in F}'ler a noktasının koordinatlarıdır ve +işlemi F cismine aittir.

Bu bağıntının bir denklik bağıntısı olduğu kolaylıkla görülebilir. O halde vektör, . Böylece denklik sınıfı temsilcisini koyu harfle gösterirsek, bir vektör

a={a|a∼b}{\displaystyle \mathbf {a} =\{a|a\sim b\}}{\displaystyle \mathbf {a} =\{a|a\sim b\}}

olarak tanımlanmış olur. Daha açık bir biçimde bir vektör,

a=(a1−b1,a2−b2,⋯,an−bn)=(c1−d1,c2−d2,⋯,cn−dn){\displaystyle \mathbf {a} =(a_{1}-b_{1},a_{2}-b_{2},\cdots ,a_{n}-b_{n})=(c_{1}-d_{1},c_{2}-d_{2},\cdots ,c_{n}-d_{n})}{\displaystyle \mathbf {a} =(a_{1}-b_{1},a_{2}-b_{2},\cdots ,a_{n}-b_{n})=(c_{1}-d_{1},c_{2}-d_{2},\cdots ,c_{n}-d_{n})}

şeklinde düşünülebilir.

Gösterimi

Bir vektör çok çeşitli şekillerde gösterimlenebilir. En yaygın gösterimler, üzerinde bir ok işareti (a→{\displaystyle {\vec {a}}}{\displaystyle {\vec {a}}}) ya da koyu harf (a{\displaystyle \mathbf {a} }{\displaystyle \mathbf {a} }) gösterimidir. Oklu gösterimin avantajı el yazılarında kolaylıkla kullanılabilir olmasıdır. Ancak baskı ve sayısal metinlerde koyu harf kullanmak adettir.

Vektörün bileşenleriyle gösteriminde ise genellikle kullanılır.

a=(a1,a2,⋯,an){\displaystyle \mathbf {a} =(a_{1},a_{2},\cdots ,a_{n})}{\displaystyle \mathbf {a} =(a_{1},a_{2},\cdots ,a_{n})}

Yer yer (konunun veriliş tarzına bağlı olarak) ya da gösterimi de yeğlenir.

a=[a1a2⋯an]{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{1}&a_{2}&\cdots &a_{n}\end{bmatrix}}}{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{1}&a_{2}&\cdots &a_{n}\end{bmatrix}}} ya daa=[a1a2⋯an]{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{1}\\a_{2}\\\cdots \\a_{n}\end{bmatrix}}}{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{1}\\a_{2}\\\cdots \\a_{n}\end{bmatrix}}}

Yine yaygın gösterimlerden biri birim vektör gösterimidir.

a=a1i1+a2i2+⋯+anin{\displaystyle \mathbf {a} =a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+\cdots +a_{n}\mathbf {i} _{n}}{\displaystyle \mathbf {a} =a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+\cdots +a_{n}\mathbf {i} _{n}}

ki burada

i1=(1,0,⋯,0){\displaystyle \mathbf {i} _{1}=(1,0,\cdots ,0)}{\displaystyle \mathbf {i} _{1}=(1,0,\cdots ,0)}
i2=(0,1,0,⋯,0){\displaystyle \mathbf {i} _{2}=(0,1,0,\cdots ,0)}{\displaystyle \mathbf {i} _{2}=(0,1,0,\cdots ,0)}
⋮{\displaystyle \vdots }{\displaystyle \vdots }
in=(0,⋯,0,1){\displaystyle \mathbf {i} _{n}=(0,\cdots ,0,1)}{\displaystyle \mathbf {i} _{n}=(0,\cdots ,0,1)}

alınabilir.

Bir vektör

a=∑j=1najij{\displaystyle \mathbf {a} =\sum _{j=1}^{n}a_{j}\mathbf {i} _{j}}{\displaystyle \mathbf {a} =\sum _{j=1}^{n}a_{j}\mathbf {i} _{j}}

şeklinde düşünüldüğünde kullanılarak

a=ajij(j=1,2,⋯,n){\displaystyle a=a_{j}\mathbf {i} _{j}\quad \quad \quad (j=1,2,\cdots ,n)}{\displaystyle a=a_{j}\mathbf {i} _{j}\quad \quad \quad (j=1,2,\cdots ,n)}

şeklinde gösterilebilir. Bu gösterim, kurtulmada ve bileşenleri temsil edecek şekilde bir kolaylık sağlamaktadır. Genellikle tensör gösterimi olarak anılır.

Eşitlik

Ancak vektörlerden birinin her bileşeni karşılıklı olarak diğerininkine eşitse bu iki vektör eşittir.

a=b{\displaystyle \mathbf {a} =\mathbf {b} }{\displaystyle \mathbf {a} =\mathbf {b} }

Vektör toplamı

image

İki vektörün toplamı üçüncü bir vektöre eşittir. 1. şekil parelelkenar metodu,2.si ise uç uca ekleme metodudur.

a+b{\displaystyle \mathbf {a} +\mathbf {b} }{\displaystyle \mathbf {a} +\mathbf {b} } =(a1i1+a2i2+⋯+anin)+(b1i1+b2i2+⋯+bnin){\displaystyle =(a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+\cdots +a_{n}\mathbf {i} _{n})+(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+\cdots +b_{n}\mathbf {i} _{n})}{\displaystyle =(a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+\cdots +a_{n}\mathbf {i} _{n})+(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+\cdots +b_{n}\mathbf {i} _{n})}
=(a1+b1)i1+(a2+b2)i2+⋯+(an+bn)in{\displaystyle =(a_{1}+b_{1})\mathbf {i} _{1}+(a_{2}+b_{2})\mathbf {i} _{2}+\cdots +(a_{n}+b_{n})\mathbf {i} _{n}}{\displaystyle =(a_{1}+b_{1})\mathbf {i} _{1}+(a_{2}+b_{2})\mathbf {i} _{2}+\cdots +(a_{n}+b_{n})\mathbf {i} _{n}}
=[a1+bna2+bn⋯a3+bn]{\displaystyle ={\begin{bmatrix}a_{1}+b_{n}\\a_{2}+b_{n}\\\cdots \\a_{3}+b_{n}\end{bmatrix}}}{\displaystyle ={\begin{bmatrix}a_{1}+b_{n}\\a_{2}+b_{n}\\\cdots \\a_{3}+b_{n}\end{bmatrix}}}

Skaler (sayıl) ile çarpma

Bir vektör uzayında, skaler ve vektörler arasında bir çarpma ve dağılma olması gerekir. r,s sayılları F cismine ait olsun. O halde a{\displaystyle \mathbf {a} }{\displaystyle \mathbf {a} }, b{\displaystyle \mathbf {b} }{\displaystyle \mathbf {b} }vektörleri için,

  • ile birleşme: r(sa)=(rs)a{\displaystyle r(s\mathbf {a} )=(rs)\mathbf {a} }{\displaystyle r(s\mathbf {a} )=(rs)\mathbf {a} }
  • toplaması üzerine dağılma: (r+s)a=ra+sa{\displaystyle (r+s)\mathbf {a} =r\mathbf {a} +s\mathbf {a} }{\displaystyle (r+s)\mathbf {a} =r\mathbf {a} +s\mathbf {a} }
  • Vektör toplamı üzerine dağılma: r(a+b)=ra+rb{\displaystyle r(\mathbf {a} +\mathbf {b} )=r\mathbf {a} +r\mathbf {b} }{\displaystyle r(\mathbf {a} +\mathbf {b} )=r\mathbf {a} +r\mathbf {b} }
  • birim öge ile çarpma: 1a=a{\displaystyle 1\mathbf {a} =\mathbf {a} }{\displaystyle 1\mathbf {a} =\mathbf {a} }

özellikleri sağlanır.

Genel olarak vektörle skalerle çarpması, vektörün her bileşeninin skaler ile çarpılmasıdır.

ra=[ra1ra2⋯ran]{\displaystyle r\mathbf {a} ={\begin{bmatrix}ra_{1}&ra_{2}&\cdots &ra_{n}\end{bmatrix}}}{\displaystyle r\mathbf {a} ={\begin{bmatrix}ra_{1}&ra_{2}&\cdots &ra_{n}\end{bmatrix}}}

Doğrudan çarpım (tensör çarpımı)

İki vektörün doğrudan çarpımının sonucu ne bir vektördür ne bir skalerdir, bir (dyad).

ab=[a1a2a3][b1b2b3]=[a1b1a1b2a1b3a2b1a2b2a2b3a3b1a3b2a3b3]{\displaystyle \mathbf {a} \mathbf {b} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}{\begin{bmatrix}b_{1}&&b_{2}&&b_{3}\end{bmatrix}}={\begin{bmatrix}a_{1}b_{1}&&a_{1}b_{2}&&a_{1}b_{3}\\a_{2}b_{1}&&a_{2}b_{2}&&a_{2}b_{3}\\a_{3}b_{1}&&a_{3}b_{2}&&a_{3}b_{3}\end{bmatrix}}}{\displaystyle \mathbf {a} \mathbf {b} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}{\begin{bmatrix}b_{1}&&b_{2}&&b_{3}\end{bmatrix}}={\begin{bmatrix}a_{1}b_{1}&&a_{1}b_{2}&&a_{1}b_{3}\\a_{2}b_{1}&&a_{2}b_{2}&&a_{2}b_{3}\\a_{3}b_{1}&&a_{3}b_{2}&&a_{3}b_{3}\end{bmatrix}}}

Bu çarpıma, eğer vektörler eş boyutluysa, çiftli (dyadic) çarpım denir. Eğer vektöreri birim vektörlerle ifade edersek

a=a1i1+a2i2+a3i3{\displaystyle \mathbf {a} =a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3}}{\displaystyle \mathbf {a} =a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3}}
b=b1i1+b2i2+b3i3{\displaystyle \mathbf {b} =b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3}}{\displaystyle \mathbf {b} =b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3}}

şeklinde tanımlanan iki vektör için doğrudan çarpım

ab{\displaystyle \mathbf {a} \mathbf {b} \,}{\displaystyle \mathbf {a} \mathbf {b} \,} = (a1i1+a2i2+a3i3)(b1i1+b2i2+b3i3){\displaystyle (a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3})(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3})}{\displaystyle (a_{1}\mathbf {i} _{1}+a_{2}\mathbf {i} _{2}+a_{3}\mathbf {i} _{3})(b_{1}\mathbf {i} _{1}+b_{2}\mathbf {i} _{2}+b_{3}\mathbf {i} _{3})}
= a1b1i1i1+a1b2i1i2+a1b3i1i3{\displaystyle a_{1}b_{1}\mathbf {i} _{1}\mathbf {i} _{1}+a_{1}b_{2}\mathbf {i} _{1}\mathbf {i} _{2}+a_{1}b_{3}\mathbf {i} _{1}\mathbf {i} _{3}}{\displaystyle a_{1}b_{1}\mathbf {i} _{1}\mathbf {i} _{1}+a_{1}b_{2}\mathbf {i} _{1}\mathbf {i} _{2}+a_{1}b_{3}\mathbf {i} _{1}\mathbf {i} _{3}}
+ a2b1i2i1+a2b2i2i2+a2b3i2i3{\displaystyle a_{2}b_{1}\mathbf {i} _{2}\mathbf {i} _{1}+a_{2}b_{2}\mathbf {i} _{2}\mathbf {i} _{2}+a_{2}b_{3}\mathbf {i} _{2}\mathbf {i} _{3}}{\displaystyle a_{2}b_{1}\mathbf {i} _{2}\mathbf {i} _{1}+a_{2}b_{2}\mathbf {i} _{2}\mathbf {i} _{2}+a_{2}b_{3}\mathbf {i} _{2}\mathbf {i} _{3}}
+ a3b1i3i1+a3b2i3i2+a3b3i3i3{\displaystyle a_{3}b_{1}\mathbf {i} _{3}\mathbf {i} _{1}+a_{3}b_{2}\mathbf {i} _{3}\mathbf {i} _{2}+a_{3}b_{3}\mathbf {i} _{3}\mathbf {i} _{3}}{\displaystyle a_{3}b_{1}\mathbf {i} _{3}\mathbf {i} _{1}+a_{3}b_{2}\mathbf {i} _{3}\mathbf {i} _{2}+a_{3}b_{3}\mathbf {i} _{3}\mathbf {i} _{3}}

olarak elde edilir. Buradaki i1i2{\displaystyle \mathbf {i} _{1}\mathbf {i} _{2}}{\displaystyle \mathbf {i} _{1}\mathbf {i} _{2}} gibi birimler yeni birer birimdir, yâni başka bir i{\displaystyle \mathbf {i} }{\displaystyle \mathbf {i} } cinsinden ifade edilemez. Bu yüzdeniij=iiij{\displaystyle \mathbf {i} _{ij}=\mathbf {i} _{i}\mathbf {i} _{j}}{\displaystyle \mathbf {i} _{ij}=\mathbf {i} _{i}\mathbf {i} _{j}} olarak tanımlandığında

{\displaystyle \quad }{\displaystyle \quad } = a1b1i11+a1b2i12+a1b3i13{\displaystyle a_{1}b_{1}\mathbf {i} _{11}+a_{1}b_{2}\mathbf {i} _{12}+a_{1}b_{3}\mathbf {i} _{13}}{\displaystyle a_{1}b_{1}\mathbf {i} _{11}+a_{1}b_{2}\mathbf {i} _{12}+a_{1}b_{3}\mathbf {i} _{13}}
+ a2b1i21+a2b2i22+a2b3i23{\displaystyle a_{2}b_{1}\mathbf {i} _{21}+a_{2}b_{2}\mathbf {i} _{22}+a_{2}b_{3}\mathbf {i} _{23}}{\displaystyle a_{2}b_{1}\mathbf {i} _{21}+a_{2}b_{2}\mathbf {i} _{22}+a_{2}b_{3}\mathbf {i} _{23}}
+ a3b1i31+a3b2i32+a3b3i33{\displaystyle a_{3}b_{1}\mathbf {i} _{31}+a_{3}b_{2}\mathbf {i} _{32}+a_{3}b_{3}\mathbf {i} _{33}}{\displaystyle a_{3}b_{1}\mathbf {i} _{31}+a_{3}b_{2}\mathbf {i} _{32}+a_{3}b_{3}\mathbf {i} _{33}}

elde edilir ki bu da dizey gösterimine tekâbül eder.

Konum (yer) vektörü

image
Kartezyen koordinat düzleminde bir konum(yer) vektörü. Vektörün koordinatları: A vektörü = (2,3)

Başlangıç noktası orijin olan vektörlere konum(yer) vektörü denir. Eğer vektör orjinde değilse vektörün uzunluğu ve yönünü değiştirmemek kaydıyla orjine taşıyabiliriz.

Başlangıç noktası O = (0,0), bitiş noktası A = (2,3) olan iki boyutlu bir vektör düşünelim. Bu vektör basit olarak aşağıdaki şekilde gösterilebilir:

A→=(2,3){\displaystyle {\overrightarrow {A}}=(2,3)}{\displaystyle {\overrightarrow {A}}=(2,3)}

Üç boyutlu kartezyen koordinat sisteminde (veya R3{\displaystyle \mathbb {R} ^{3}}{\displaystyle \mathbb {R} ^{3}}) vektörler, üç skaler sayı ile tanımlanır:

G→=(a,b,c){\displaystyle {\overrightarrow {G}}=(a,b,c)}{\displaystyle {\overrightarrow {G}}=(a,b,c)}

Standart temel vektörler

image
"i","j","k" temel birim vektörleri.

Birim vektör, uzunluğu 1 birim olan vektörlere denir. Üç boyutlu kartezyen koordinat sisteminde x,y ve z eksenleri üzerinde yer alan üç tane temel birim vektör vardır. Bunlar:

i=e1=(1,0,0){\displaystyle i={\mathbf {e} }_{1}=(1,0,0)}{\displaystyle i={\mathbf {e} }_{1}=(1,0,0)}
j=e2=(0,1,0){\displaystyle j={\mathbf {e} }_{2}=(0,1,0)}{\displaystyle j={\mathbf {e} }_{2}=(0,1,0)}
k=e3=(0,0,1){\displaystyle k={\mathbf {e} }_{3}=(0,0,1)}{\displaystyle k={\mathbf {e} }_{3}=(0,0,1)}

ise:

G→=(a,b,c)=ai+bj+ck{\displaystyle {\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }}{\displaystyle {\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }}

Bir vektörün normu

A vektörünün uzunluğu (normu ya da boyu), ||A|| sembolü ile gösterilir.

"i", "j" ve "k" temel birim vektörleri cinsinden yazılan bir vektörün uzunluk formülü, Pisagor teoreminin bir sonucudur. O halde:

G→=(a,b,c)=ai+bj+ck{\displaystyle {\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }}{\displaystyle {\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }}

Yukarıdaki vektörü ele alırsak:

‖G→‖=a2+b2+c2{\displaystyle \left\|{\overrightarrow {G}}\right\|={\sqrt {{a}^{2}+{b}^{2}+{c}^{2}}}}{\displaystyle \left\|{\overrightarrow {G}}\right\|={\sqrt {{a}^{2}+{b}^{2}+{c}^{2}}}}

İki vektörün birbiriyle çarpımı

G→=(a,b,c){\displaystyle {\overrightarrow {G}}=(a,b,c)}image
H→=(d,e,f){\displaystyle {\overrightarrow {H}}=(d,e,f)}image

Bu iki vektörü ele alırsak:

İç (Skaler) çarpım (G→⋅H→{\displaystyle {\overrightarrow {G}}\cdot {\overrightarrow {H}}}image)

Nokta çarpım da denilen çarpım yöntemiyle yapılan çarpımdır.

Bileşenleri türünden çarpımı

Örnek:

G→=(a,b,c){\displaystyle {\overrightarrow {G}}=(a,b,c)}image
H→=(d,e,f){\displaystyle {\overrightarrow {H}}=(d,e,f)}image

Bu iki vektörü ele alırsak:

G→⋅H→=(a,b,c)⋅(d,e,f)=a⋅d+b⋅e+c⋅f{\displaystyle {\overrightarrow {G}}\cdot {\overrightarrow {H}}={(a,b,c)}\cdot {(d,e,f)}={a}\cdot {d}+{b}\cdot {e}+{c}\cdot {f}}image

Aralarındaki açı türünden çarpımı

image
A→{\displaystyle {\overrightarrow {A}}}image ve B→{\displaystyle {\overrightarrow {B}}}image vektörleri arasındaki "theta" açısı.

Örnek:

G→=(a,b,c){\displaystyle {\overrightarrow {G}}=(a,b,c)}image
H→=(d,e,f){\displaystyle {\overrightarrow {H}}=(d,e,f)}image

Bu iki vektörü ele alırsak:

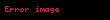
G→⋅H→=‖G→‖‖H→‖cos⁡θ{\displaystyle {\overrightarrow {G}}\cdot {\overrightarrow {H}}=\left\|{\overrightarrow {G}}\right\|\left\|{\overrightarrow {H}}\right\|\cos \theta }image

cos⁡θ{\displaystyle \cos \theta }image 'nın değerini bulmak için:

cos⁡θ=G→⋅H→‖G→‖‖H→‖{\displaystyle \cos \theta ={\frac {{\overrightarrow {G}}\cdot {\overrightarrow {H}}}{\left\|{\overrightarrow {G}}\right\|\left\|{\overrightarrow {H}}\right\|}}}image

Vektörel çarpım (G→×H→{\displaystyle {\overrightarrow {G}}\times {\overrightarrow {H}}}image)

Çapraz çarpım da denilen çarpım yöntemiyle yapılan çarpımdır.

Örnek:

G→=(a,b,c)=ai+bj+ck{\displaystyle {\overrightarrow {G}}=(a,b,c)=a{\mathbf {i} }+b{\mathbf {j} }+c{\mathbf {k} }}image
H→=(d,e,f)=di+ej+fk{\displaystyle {\overrightarrow {H}}=(d,e,f)=d{\mathbf {i} }+e{\mathbf {j} }+f{\mathbf {k} }}image

Bu iki vektörü ele alırsak:

G→×H→{\displaystyle {\overrightarrow {G}}\times {\overrightarrow {H}}}image =|ijkabcdef|{\displaystyle ={\begin{vmatrix}\mathbf {i} &&\mathbf {j} &&\mathbf {k} \\a&&b&&c\\d&&e&&f\end{vmatrix}}}image
{\displaystyle \quad }image

Yukarıdaki problem bir determinant problemidir. Sarrus kuralı ile hesaplanır.

Kaynakça

  1. ^ Ivanov 2001
  2. ^ Heinbockel 2001
  3. ^ Itô 1993, s. 1678; Pedoe 1988
  4. ^ "Online Etymology Dictionary". 18 Ağustos 2006 tarihinde kaynağından . Erişim tarihi: 25 Ocak 2007. 
  5. ^ Türk Dil Kurumu, Bilim ve Sanat Terimleri Ana Sözlüğü[]

Ek kaynaklar

  • Ivanov, A.B. (2001), "Vector", Hazewinkel, Michiel (Ed.), Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN  .
  • Heinbockel, J. H. (2001), Introduction to Tensor Calculus and Continuum Mechanics, Trafford Publishing, ISBN , 6 Ocak 2020 tarihinde kaynağından , erişim tarihi: 30 Eylül 2022 

Dış bağlantılar

wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar

Matematik fizik ve muhendislikte Oklid vektoru veya kisaca vektor bazen geometrik vektor konumsal vektor ya da yoney sayisal buyuklugu veya uzunlugu ve yonu olan geometrik bir objedir Vektor genellikle bir dogru parcasi ile ozdeslestirilir Bir baslangic noktasi A ile bir uc noktasi B yi birlestiren bir ok seklinde gorsellestirilir ve AB displaystyle overrightarrow AB ile belirtilir A noktasindan B noktasina cizili bir vektor Hiz kuvvet ivme ve agirlik ornek birer vektorel niceliktir Vektorler bir sayi skaler ile veya baska bir vektor ile carpilabilir ve bolunebilir Ayni zamanda yonu degistirilmemek sarti ile otelenebilirler Vektorlerin yonlu dogru parcalarindan farki budur Yonlu dogru parcalarinin koordinat sistemindeki yeri sabitken vektorler otelenebilirler Koken Ingilizcede bu yapi icin kullanilan sozcuk vector dur Kokeni tasimak bir yone aktarmak gondermek anlamina gelen vehere Latince fiil govdesidir Sozcugun anlami tasiyici yoncu olarak dusunulebilir Bu yuzden olabilir ki Turkcede buyuk ihtimalle Fransizcadan devsirilmis olan vektor karsiligindan sonra yoney karsiligi kullanilmaktadir Gosterimi A noktasindan B noktasina varan bir vektor oku Fiziksel vektorler veya geometrik vektorler iki boyutlu duzlem icin tanimi su sekilde yapilabilir Iki boyutlu duzlemde 2 tane nokta alinsin bu noktalar A ve B noktalari olsun A noktasindan baslangic noktasi B noktasina bitis noktasi cizilen ve normu olan bu yonlu dogru parcasina A dan B ye cizilen AB vektoru denir Gosterimi iki sekildedir 1 gosterim AB displaystyle overrightarrow mathrm A mathrm B 2 gosterim AB ile gosterilir Ok vektorun yonunu gosterir Dogru parcasinin uzunlugu ise vektor buyuklugu ile dogru orantilidir Iki boyutlu bir bazen bir vektor koordinat duzlemine dik olarak gosterilmesi gerekebilir Bir dairenin merkezinde bir nokta bulunursa bu sembol yonu gozlemciye dogru olan bir vektoru gostermektedir Bir dairenin icinde bir carpi isareti bulunursa bu sembol yonu duzlemin arkasina dogru olan bir vektoru gostermektedir Bu semboller bir savas okunun ucunun goruntulenmesi ve bir savas okunun arka kanatlarinin goruntulenmesi gibi dusunulebilir Bir vektorun buyuklugu Bir vektorun buyuklugu baslangic ve bitis noktalari arasinda kalan dogru parcasinin uzunlugudur vektorler referans noktasina gore ve olmak uzere iki yone ayrilabilirler yonundeki vektore negatif yonlu vektor yonundeki vektere pozitif yonlu vektor denir Vektorlerin buyuklukleri skaler nicelik ifade eder o denli bu ve isaretlerinin skaler bir gosterimden uzaklasmasi icin vektorun mutlak degerini almamiz gerekir e a AB vektorunun normu AB dir Daha genel gosterim AB displaystyle overrightarrow mathrm A mathrm B dir Soyut tanimi Soyut olarak vektorler bir F cisminin uzerine tanimli bir vektor uzayinin ogeleridir Vektorler bu cisim uzerine tanimlanmis bir denklik bagintisi yardimiyla tanimlanabilir a b c d Fn F F F displaystyle a b c d in F n F times F times cdots times F n tane olsun a ogesi ile b ogesi ancak bilesenlerin toplami olarak a d b c ise bagintilidir Daha bicimsel olmak gerekirse a b i 1 2 n ai di bi ci displaystyle a sim b Leftrightarrow forall i in 1 2 cdots n quad a i d i b i c i seklinde tanimlanir ki burada ai F displaystyle a i in F ler a noktasinin koordinatlaridir ve islemi F cismine aittir Bu bagintinin bir denklik bagintisi oldugu kolaylikla gorulebilir O halde vektor Boylece denklik sinifi temsilcisini koyu harfle gosterirsek bir vektor a a a b displaystyle mathbf a a a sim b olarak tanimlanmis olur Daha acik bir bicimde bir vektor a a1 b1 a2 b2 an bn c1 d1 c2 d2 cn dn displaystyle mathbf a a 1 b 1 a 2 b 2 cdots a n b n c 1 d 1 c 2 d 2 cdots c n d n seklinde dusunulebilir Gosterimi Bir vektor cok cesitli sekillerde gosterimlenebilir En yaygin gosterimler uzerinde bir ok isareti a displaystyle vec a ya da koyu harf a displaystyle mathbf a gosterimidir Oklu gosterimin avantaji el yazilarinda kolaylikla kullanilabilir olmasidir Ancak baski ve sayisal metinlerde koyu harf kullanmak adettir Vektorun bilesenleriyle gosteriminde ise genellikle kullanilir a a1 a2 an displaystyle mathbf a a 1 a 2 cdots a n Yer yer konunun verilis tarzina bagli olarak ya da gosterimi de yeglenir a a1a2 an displaystyle mathbf a begin bmatrix a 1 amp a 2 amp cdots amp a n end bmatrix ya daa a1a2 an displaystyle mathbf a begin bmatrix a 1 a 2 cdots a n end bmatrix Yine yaygin gosterimlerden biri birim vektor gosterimidir a a1i1 a2i2 anin displaystyle mathbf a a 1 mathbf i 1 a 2 mathbf i 2 cdots a n mathbf i n ki burada i1 1 0 0 displaystyle mathbf i 1 1 0 cdots 0 i2 0 1 0 0 displaystyle mathbf i 2 0 1 0 cdots 0 displaystyle vdots in 0 0 1 displaystyle mathbf i n 0 cdots 0 1 dd alinabilir Bir vektor a j 1najij displaystyle mathbf a sum j 1 n a j mathbf i j seklinde dusunuldugunde kullanilarak a ajij j 1 2 n displaystyle a a j mathbf i j quad quad quad j 1 2 cdots n seklinde gosterilebilir Bu gosterim kurtulmada ve bilesenleri temsil edecek sekilde bir kolaylik saglamaktadir Genellikle tensor gosterimi olarak anilir Esitlik Ancak vektorlerden birinin her bileseni karsilikli olarak digerininkine esitse bu iki vektor esittir a b displaystyle mathbf a mathbf b Vektor toplami Iki vektorun toplami ucuncu bir vektore esittir 1 sekil parelelkenar metodu 2 si ise uc uca ekleme metodudur a b displaystyle mathbf a mathbf b a1i1 a2i2 anin b1i1 b2i2 bnin displaystyle a 1 mathbf i 1 a 2 mathbf i 2 cdots a n mathbf i n b 1 mathbf i 1 b 2 mathbf i 2 cdots b n mathbf i n a1 b1 i1 a2 b2 i2 an bn in displaystyle a 1 b 1 mathbf i 1 a 2 b 2 mathbf i 2 cdots a n b n mathbf i n a1 bna2 bn a3 bn displaystyle begin bmatrix a 1 b n a 2 b n cdots a 3 b n end bmatrix Skaler sayil ile carpma Bir vektor uzayinda skaler ve vektorler arasinda bir carpma ve dagilma olmasi gerekir r s sayillari F cismine ait olsun O halde a displaystyle mathbf a b displaystyle mathbf b vektorleri icin ile birlesme r sa rs a displaystyle r s mathbf a rs mathbf a toplamasi uzerine dagilma r s a ra sa displaystyle r s mathbf a r mathbf a s mathbf a Vektor toplami uzerine dagilma r a b ra rb displaystyle r mathbf a mathbf b r mathbf a r mathbf b birim oge ile carpma 1a a displaystyle 1 mathbf a mathbf a ozellikleri saglanir Genel olarak vektorle skalerle carpmasi vektorun her bileseninin skaler ile carpilmasidir ra ra1ra2 ran displaystyle r mathbf a begin bmatrix ra 1 amp ra 2 amp cdots amp ra n end bmatrix Dogrudan carpim tensor carpimi Iki vektorun dogrudan carpiminin sonucu ne bir vektordur ne bir skalerdir bir dyad ab a1a2a3 b1b2b3 a1b1a1b2a1b3a2b1a2b2a2b3a3b1a3b2a3b3 displaystyle mathbf a mathbf b begin bmatrix a 1 a 2 a 3 end bmatrix begin bmatrix b 1 amp amp b 2 amp amp b 3 end bmatrix begin bmatrix a 1 b 1 amp amp a 1 b 2 amp amp a 1 b 3 a 2 b 1 amp amp a 2 b 2 amp amp a 2 b 3 a 3 b 1 amp amp a 3 b 2 amp amp a 3 b 3 end bmatrix Bu carpima eger vektorler es boyutluysa ciftli dyadic carpim denir Eger vektoreri birim vektorlerle ifade edersek a a1i1 a2i2 a3i3 displaystyle mathbf a a 1 mathbf i 1 a 2 mathbf i 2 a 3 mathbf i 3 b b1i1 b2i2 b3i3 displaystyle mathbf b b 1 mathbf i 1 b 2 mathbf i 2 b 3 mathbf i 3 seklinde tanimlanan iki vektor icin dogrudan carpim ab displaystyle mathbf a mathbf b a1i1 a2i2 a3i3 b1i1 b2i2 b3i3 displaystyle a 1 mathbf i 1 a 2 mathbf i 2 a 3 mathbf i 3 b 1 mathbf i 1 b 2 mathbf i 2 b 3 mathbf i 3 a1b1i1i1 a1b2i1i2 a1b3i1i3 displaystyle a 1 b 1 mathbf i 1 mathbf i 1 a 1 b 2 mathbf i 1 mathbf i 2 a 1 b 3 mathbf i 1 mathbf i 3 a2b1i2i1 a2b2i2i2 a2b3i2i3 displaystyle a 2 b 1 mathbf i 2 mathbf i 1 a 2 b 2 mathbf i 2 mathbf i 2 a 2 b 3 mathbf i 2 mathbf i 3 a3b1i3i1 a3b2i3i2 a3b3i3i3 displaystyle a 3 b 1 mathbf i 3 mathbf i 1 a 3 b 2 mathbf i 3 mathbf i 2 a 3 b 3 mathbf i 3 mathbf i 3 olarak elde edilir Buradaki i1i2 displaystyle mathbf i 1 mathbf i 2 gibi birimler yeni birer birimdir yani baska bir i displaystyle mathbf i cinsinden ifade edilemez Bu yuzdeniij iiij displaystyle mathbf i ij mathbf i i mathbf i j olarak tanimlandiginda displaystyle quad a1b1i11 a1b2i12 a1b3i13 displaystyle a 1 b 1 mathbf i 11 a 1 b 2 mathbf i 12 a 1 b 3 mathbf i 13 a2b1i21 a2b2i22 a2b3i23 displaystyle a 2 b 1 mathbf i 21 a 2 b 2 mathbf i 22 a 2 b 3 mathbf i 23 a3b1i31 a3b2i32 a3b3i33 displaystyle a 3 b 1 mathbf i 31 a 3 b 2 mathbf i 32 a 3 b 3 mathbf i 33 dd elde edilir ki bu da dizey gosterimine tekabul eder Konum yer vektoru Kartezyen koordinat duzleminde bir konum yer vektoru Vektorun koordinatlari A vektoru 2 3 Baslangic noktasi orijin olan vektorlere konum yer vektoru denir Eger vektor orjinde degilse vektorun uzunlugu ve yonunu degistirmemek kaydiyla orjine tasiyabiliriz Baslangic noktasi O 0 0 bitis noktasi A 2 3 olan iki boyutlu bir vektor dusunelim Bu vektor basit olarak asagidaki sekilde gosterilebilir A 2 3 displaystyle overrightarrow A 2 3 Uc boyutlu kartezyen koordinat sisteminde veya R3 displaystyle mathbb R 3 vektorler uc skaler sayi ile tanimlanir G a b c displaystyle overrightarrow G a b c Standart temel vektorler i j k temel birim vektorleri Birim vektor uzunlugu 1 birim olan vektorlere denir Uc boyutlu kartezyen koordinat sisteminde x y ve z eksenleri uzerinde yer alan uc tane temel birim vektor vardir Bunlar i e1 1 0 0 displaystyle i mathbf e 1 1 0 0 j e2 0 1 0 displaystyle j mathbf e 2 0 1 0 k e3 0 0 1 displaystyle k mathbf e 3 0 0 1 ise G a b c ai bj ck displaystyle overrightarrow G a b c a mathbf i b mathbf j c mathbf k dd Bir vektorun normu A vektorunun uzunlugu normu ya da boyu A sembolu ile gosterilir i j ve k temel birim vektorleri cinsinden yazilan bir vektorun uzunluk formulu Pisagor teoreminin bir sonucudur O halde G a b c ai bj ck displaystyle overrightarrow G a b c a mathbf i b mathbf j c mathbf k Yukaridaki vektoru ele alirsak G a2 b2 c2 displaystyle left overrightarrow G right sqrt a 2 b 2 c 2 Iki vektorun birbiriyle carpimiG a b c displaystyle overrightarrow G a b c H d e f displaystyle overrightarrow H d e f Bu iki vektoru ele alirsak Ic Skaler carpim G H displaystyle overrightarrow G cdot overrightarrow H Nokta carpim da denilen carpim yontemiyle yapilan carpimdir Bilesenleri turunden carpimi Ornek G a b c displaystyle overrightarrow G a b c H d e f displaystyle overrightarrow H d e f Bu iki vektoru ele alirsak G H a b c d e f a d b e c f displaystyle overrightarrow G cdot overrightarrow H a b c cdot d e f a cdot d b cdot e c cdot f Aralarindaki aci turunden carpimi A displaystyle overrightarrow A ve B displaystyle overrightarrow B vektorleri arasindaki theta acisi Ornek G a b c displaystyle overrightarrow G a b c H d e f displaystyle overrightarrow H d e f Bu iki vektoru ele alirsak G H G H cos 8 displaystyle overrightarrow G cdot overrightarrow H left overrightarrow G right left overrightarrow H right cos theta cos 8 displaystyle cos theta nin degerini bulmak icin cos 8 G H G H displaystyle cos theta frac overrightarrow G cdot overrightarrow H left overrightarrow G right left overrightarrow H right Vektorel carpim G H displaystyle overrightarrow G times overrightarrow H Capraz carpim da denilen carpim yontemiyle yapilan carpimdir Ornek G a b c ai bj ck displaystyle overrightarrow G a b c a mathbf i b mathbf j c mathbf k H d e f di ej fk displaystyle overrightarrow H d e f d mathbf i e mathbf j f mathbf k Bu iki vektoru ele alirsak G H displaystyle overrightarrow G times overrightarrow H ijkabcdef displaystyle begin vmatrix mathbf i amp amp mathbf j amp amp mathbf k a amp amp b amp amp c d amp amp e amp amp f end vmatrix displaystyle quad Yukaridaki problem bir determinant problemidir Sarrus kurali ile hesaplanir Kaynakca Ivanov 2001 Heinbockel 2001 Ito 1993 s 1678 Pedoe 1988 Online Etymology Dictionary 18 Agustos 2006 tarihinde kaynagindan Erisim tarihi 25 Ocak 2007 Turk Dil Kurumu Bilim ve Sanat Terimleri Ana Sozlugu olu kirik baglanti Ek kaynaklar Ivanov A B 2001 Vector Hazewinkel Michiel Ed Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Heinbockel J H 2001 Introduction to Tensor Calculus and Continuum Mechanics Trafford Publishing ISBN 1 55369 133 4 6 Ocak 2020 tarihinde kaynagindan erisim tarihi 30 Eylul 2022 Dis baglantilar

Yayın tarihi: Temmuz 01, 2024, 18:27 pm
En çok okunan
  • Aralık 01, 2024

    Berberis sellowiana

  • Aralık 01, 2024

    Berberis setosa

  • Aralık 01, 2024

    Berberis setigrifolia

  • Aralık 01, 2024

    Berberis schwerinii

  • Aralık 01, 2024

    Berberis schochii

Günlük

  • Orhan Eskiköy

  • Maraş Katliamı

  • Kürtler

  • Babamın Sesi

  • 2 Aralık

  • 1993

  • 3 Aralık

  • Avustralya 31-0 Amerikan Samoası

  • Avustralya millî futbol takımı

  • Göl

NiNa.Az - Stüdyo

  • Vikipedi

Bültene üye ol

Mail listemize abone olarak bizden her zaman en son haberleri alacaksınız.
Temasta ol
Bize Ulaşın
DMCA Sitemap Feeds
© 2019 nina.az - Her hakkı saklıdır.
Telif hakkı: Dadaş Mammedov
Üst