İş (fizik)

Fizikte, bir kuvvet bir cisim üzerine etki ettiğinde ve kuvvetin uygulama yönünde konum değişikliği olduğunda iş yaptığı söylenir. Örneğin, bir valizi yerden kaldırdığınızda, valiz üzerine yapılan iş kaldırıldığı yükseklik süresince ağırlığını kaldırmak için aldığı kuvvettir.

İş
Bir beyzbol atıcısı top üzerinde pozitif iş yaparken çekilen fotoğraflar.
Yaygın sembol(ler):	W
SI nicelik boyutu:	1 kg·m^2/s^2
SI birimi:	joule (J)
Diğer niceliklerden türetimi:	W = F · s W = τ θ

İş terimi ilk kez 1826 yılında Fransız matematikçi Gaspard-Gustave Coriolis tarafından sel altında kalmış madenlerden suyu çıkartmak için kullanılan eski buhar makinelerinin kullanımına dayanan “yükseklik boyu kaldırılan ağırlık olarak tanımlanmıştır. Uluslararası Birimler Sistemi (SI)’ndeki iş birimi newton-metre ya da jouledür.

F genliğinde sabit bir güç tarafından bir s yerdeğişimini hareket ettiren noktaya kuvvet doğrultusunda yapılan iş üründür.

${\displaystyle W=Fs.}$

Örneğin, 10 newtonluk bir kuvvet 2 metrelik yol giden bir noktaya uygulanırsa, W = (10 N)(2 m) = 20 N m = 20 J iş yapmış olur. Bu yaklaşık olarak 1 kg ağırlığın yerden bir insanın kafa hizasına kadar yerçekimi kuvvetine karşı kaldırılırken yapılan iştir. İşin aynı yükseklikte iki kat ağırlık ya da aynı ağırlıkta iki kat yüksekliğe kaldırılmasıyla ikiye katlandığını göz önüne alın.

Birimler

İş bir metrelik mesafe boyunca bir newtonluk kuvvet tarafında harcanmış enerji olarak tanımlanan joule (J)’dür. Eş değer ölçüde Newton-metre (N•m) bazen işin ölçüm birimi olarak kullanılır fakat bu dönme momenti ölçüm birimi olan Newton-metre birimiyle karıştırılabilir. Newton-metre olarak ifade edilen niceliğin dönme momenti ölçümü mü yoksa enerji ölçümümü olduğu konusunda karışıklığa neden olabileceği için Nm kullanımı SI yetkilileri tarafından kaldırılmıştır. SI dışındaki iş birimleri erg, ayak-libre, kilovat saat, litre-atmosfer ve beygir gücü-saattir. İşin ısıyla aynı fiziksel boyuta sahip olmasından dolayı, bazen kalori, BTU gibi genel olarak ısı veya enerji içeriğine mahsus ölçüm birimleri kullanılır.

• 1 N-m = kg m²/s²
• 1 Joule (J) = 1 N-m
• 1 Joule = 0,239 Kalori (cal) veya 1 cal = 4,184 J .
• Elektronvolt (eV)
• 1 İngiliz Isı Birimi (BTU) = 1,055 J, 1 kWh = 3412 BTU veya 1 BTU = 0,0002931 kWh
• 1 Watt-saat (W.h) = 3,600 J,
• 1 Kilowatt saat (kWh) = 1000 Wh, 1 kWh = 3.600.000 J
• 1 erg (Yunanca ergon: iş) = 10⁻⁷ J
• Foot - pound (ft lb), 1 ft lb = 1.356 N-m
• litre-atmosfer (l.atm)

İş ve Enerji

İş enerji ile yakından ilişkilidir. Enerjinin korunumu yasası bir sistemin toplam iç enerjisindeki değişimin eklenen ısıdan sistem tarafından yapılan işin çıkarılmasına eşit olduğunu öne sürer.

${\displaystyle dE=\delta Q-\delta W,}$

F sembolü ısı (Q) ve işin (W) kesin olmayan diferansiyeli olduğunu gösterir. Newton’un ikinci yasasından, serbest, katı bir cisim üzerine yapılan işin bu cismin rotasyon ve süratinin kinetik enerjisindeki değişime eşit olduğu görülebilir.^[]

${\displaystyle W=\Delta KE.}$

Potansiyel fonksiyon tarafından ortaya çıkarılan iki kuvvet potansiyel enerji olarak bilinir ve bu kuvvetler korunumludur denir. Böylece yalnızca korunumlu kuvvet alanına rotasyon ve süratta değişiklik olmadan yerleştirilmiş bir nesne üzerindeki iş nesnenin (-) potansiyel enerjisinin değişimine eşittir.^[]

${\displaystyle W=-\Delta PE.}$

Bu formüller işin bir kuvvetin hareketiyle ilgili enerjisi olduğunu gösterir, yani iş sonradan enerjinin fiziksel boyutlarını ve birimlerini sahip olur.^[] Burada tartışılan iş/enerji prensipleri elektrik iş/enerji prensiplerine benzerdir.

Belirleyici Kuvvetler

Belirleyici güçler nesneyi bir sınır içerisinde kısıtlı tutan bir sistemdeki bileşenlerin hareketini belirler (yerçekimi ve bir eğim durumunda, nesne eğime yapışır, gergin bir tele tutturulduğunda teli daha da germek için ileriye doğru hareket edemez). Belirleyicinin yönündeki bütün hareketleri ortadan kaldırırlar, yani belirleyici kuvvetler o nesnenin süratı bu kuvvete 0 paralel olmaya zorlandığı için bu kuvvet dolayısıyla sistem üzerinde iş yapmazlar.^[]

Örneğin, düzgün dairesel hareket yanında bir top üzerindeki bir yay tarafından içeriye doğru uygulanan merkezcil kuvvet topu hareketini dairenin merkezinden uzağa doğru sınırlandıran dairesel harekete zorlar. Bu kuvvet sıfır iş yapar çünkü topun süratine diktir. Bir diğer örnek ise masa üzerinde duran kitaptır. Eğer masa üzerinde kayması için kitaba dış kuvvetler uygulanırsa, masa tarafından uygulanan kuvvet kitabın aşağıya doğru hareketini kısıtlar. Masa tarafından uygulanan kuvvet kitabı destekler ve hareketine dikeydir, bu da belirleyici kuvvetin iş yapmadığı anlamına gelir.^[]

Yüklü bir parçacık üzerindeki manyetik güç F = qv × B’dir, burada q yük, v parçacığın sürati ve B manyetik alan. Çapraz çarpım sonucu daima orijinal vektörlerin her ikisine de diktir, yani F ⊥ v. İki dikey vektörün iç çarpım ürünü daima sıfırdır yani iş W = F · v = 0’dır ve manyetik güç iş yapmaz. Hareketin yönünü değiştirebilir ama hiçbir zaman sürati değiştiremez.^[]

Matematiksel Hesaplama

Nesneleri hareket ettirmek için, iş/zaman niceliği mesafe/zaman ya da sürat olarak hesaplanır. Yani, herhangi bir anda, kuvvet (joules/saniye ya da watt olarak ölçülen) tarafından yapılan bir işin değeri kuvvetin ve uygulama noktasının sürat vektörünün skaler çarpımıdır. Sürat ve kuvvetin skaler çarpımı ani güç olarak sınıflandırılır. Matematik temel teoremince, süratler bütün bir mesafeyi almak için zamanla birleşebileceklerinden, bir yol boyunca toplam iş benzer şekilde uygulama noktası yörüngesi boyunca uygulanan ani gücün zaman-integralidir.

İş bir mesafe boyunca hareket eden bir nokta üzerindeki kuvvetin sonucudur. Nokta hareket ettikçe, her and X eğrisini v sürati ile takip eder. dt bir anında oluşan küçük mikardaki δW işi

${\displaystyle \delta W=\mathbf {F} \cdot d\mathbf {s} =\mathbf {F} \cdot \mathbf {v} dt}$

F.v dt anı üzerindeki güçtür. Noktanın gidişatı üzerindeki bu küçük miktardaki işlerin şu sonucu verir;

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\tfrac {d\mathbf {s} }{dt}}dt=\int _{C}\mathbf {F} \cdot d\mathbf {s} ,}$

C x(t₁) x(t₂))’e olan gidim izidir. Bu integral parçacığın gidişatı boyunca hesaplanmıştır ve bu yüzden bağımlı opsiyon denir.

Eğer kuvvet daime bu hat boyu yönlendirilirse ve kuvvetin genliği F ise, bu integral şöyle sadeleştirilir:

${\displaystyle W=\int _{C}Fds}$

s hat boyunca olan mesafedir. Eğer F hat boyunca yönelmesinin yanı sıra sabit ise o zaman integral şu şekilde sadeleştirilir:

${\displaystyle W=\int _{C}Fds=F\int _{C}ds=Fs}$

s nokta tarafından hat boyunca gidilen mesafedir.

Bu hesaplama hat boyu yönelmeyen, parçacık tarafından takip edilmeyen sabit bir güç olarak genellenebilir. Bu durumda θ’nın kuvvet vektörü ve hareket yönü arasındaki açıyı gösterdiği F·ds = Fcosθds iç çarpımı:

${\displaystyle W=\int _{C}\mathbf {F} \cdot d\mathbf {s} =Fs\cos \theta .}$

Bir cisme uygulanan kuvvetin daima sürat vektöründen 90 derece açıda olması durumunda ( bir cisim merkezcil kuvvet altında bir dairede hareket ettiğinde), 90 derecenin kosinüsü sıfır olduğunda hiç iş yapılmamış olur. Yani, dairesel yörüngeli bir gezegen (bütün yörüngeler biraz eliptik olduğu için ideal budur) üzerinde yerçekimi tarafından hiç iş yapılamaz. Ayrıca, mekanik kuvvet tarafından sınırlandırılmışken sabit bir hızda dairesel olarak hareket eden bir cisim üzerine de hiç iş yapılmaz. Örneğin sürtünmesiz ideal bir santrifüjde sabit hızla hareket etmek gibi. İşi “kuvvet çarpı düz doğru dilimi” olarak hesaplamak yukarıda da belirtildiği gibi yalnızca en basit durumlarda uygulanır. Eğer kuvvet değişiyorsa ya da cisim eğimli muhtemelen dönen ve sert olmayan bir yolda hareket ediyorsa sadece kuvvetin uygulandığı noktanın yolu ve uygulama noktasına paralel kuvvetin bileşeni sürati iş yapıyor (süratle aynı yönde pozitif, zıt yönde negatif) olur. Kuvvetin bu bileşeni skaler teğetsel bileşen denilen (F, θ kuvvet ve sürat arasındaki açı) skaler büyüklükle tanımlanabilir. Ardından işin en genel tanımı aşağıdaki gibi formüle edilebilir: Kuvvetin işi uygulama noktası yolunda skaler teğetsel bileşeninin integral hattıdır.^[]

Dönme Momenti ve Dönüş

Dönme momenti katı bir cismin iki farklı noktası üzerine etki eden eşit ve zıt kuvvetlerden kaynaklanır. Bu kuvvetlerin toplamı nötrleşir fakat cisim üzerindeki etkileri T dönme momentidir. Dönme momentinin yaptığı iş:

${\displaystyle \delta W=\mathbf {T} \cdot {\vec {\omega }}\delta t,}$

T.ω, δt anındaki güç. Katı cismin gidişatı üzerindeki bu küçük miktardaki işlerin toplamı şu sonucu verir;

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\vec {\omega }}dt.}$

Bu integral, zamanla değişen ω açısal süratiyle katı cismin gidişatı boyunca hesaplanmıştır ve bu yüzden bağımlı opsiyon denir. Eğer açısal sürat vektörü sabit bir yön belirlerse,

${\displaystyle {\vec {\omega }}={\dot {\phi }}\mathbf {S} ,}$

φ, S sabit birim vektörü civarındaki rotasyon açısı. Bu durumda, dönme momentinin işi,

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\vec {\omega }}dt=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot \mathbf {S} {\frac {d\phi }{dt}}dt=\int _{C}\mathbf {T} \cdot \mathbf {S} d\phi ,}$

C, φ(t₁) ‘den φ(t₂)'’ye olan gidim izidir. Bu integral φ(t) rotasyonel gidim izine dayanır ve dolayısıyla bağımlı opsiyondur. Eğer T dönme momenti açısal sürat vektörü ile aynı hizaya konursa,

${\displaystyle \mathbf {T} =\tau \mathbf {S} ,}$

Ve hem dönme momenti hem de açısal sürat vektörü sabitse, o zaman iş şu formu alır;

${\displaystyle W=\int _{t_{1}}^{t_{2}}\tau {\dot {\phi }}dt=\tau (\phi _{2}-\phi _{1}).}$

${\displaystyle W=\int _{t_{1}}^{t_{2}}\tau {\dot {\phi }}dt=\tau (\phi _{2}-\phi _{1}).}$

A force of constant magnitude and perpendicular to the lever arm

Bu sonuç şekilde gösterildiği gibi dönme momentinin F sabit genliğinin kuvvetinden meydana geldiğini ve r mesafesindeki kaldıraç koluna dik olarak uygulandığı göz önüne alınarak daha kolay anlaşılabilir. Bu kuvvet s=rφ dairesel yayı boyu mesafeye etki edecektir, yani yapılan iş:

${\displaystyle W=Fs=Fr\phi .}$

τ=Fr' dönme momentini elde etmek için

${\displaystyle W=Fr\phi =\tau \phi ,}$ elde etmek için yukarıdaki gibi tanıtın.

Sadece açısal sürat vektörünün yönündeki dönme momentinin bileşeninin işe katkı sağladığı görülebilir.

İş ve Potansiyel Enerji

F kuvveti ve uygulama noktasının v süratinin skaler çarpımı zamanın herhangi bir anında bir sisteme güç girişini tanımlar. Bu gücün uygulama noktası gidim izine entegrasyonu, C=x(t), güç tarafından sisteme iş girişini tanımlar.

Patika Bağımlılığı

C eğrisi boyunca hareket eden bir nesne üzerine bir F kuvveti tarafından yapılan iş çizgisel integral tarafından verilir:

${\displaystyle W=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {x} =\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt,}$

'dx(t), C gidim izi ve v bu gidim izi boyunca olan sürat. Genelde bu integral süratin belirtildiği bir patika gerektirir, bu yüzden işin değerlendirmesi bağıl opsiyondur denir.

İşin integralinin zamana göre türevi ani güç sağlar,

${\displaystyle {\frac {dW}{dt}}=P(t)=\mathbf {F} \cdot \mathbf {v} .}$

Patika Bağımsızlığı

Eğer uygulanan kuvvet için iş yoldan bağımsız ise, kuvvet tarafından yapılan iş, gradyan teoremince, uygulama noktası gidim izinin başlangıcında ve sonunca değerlendirilen potansiyel fonksiyondur. Böyle bir kuvvet korunumlu olarak adlandırılır. Bu, x(t₁) ve x(t₂) noktalarında, bu iki nokta arasındaki gidişat üzerindeki işi elde etmek için hesaplanabilen bir U (x) potansiyel fonksiyonu var demektir. Potansiyelde pozitif işte bir indirgeme olması için bu fonksiyonu negatif işaretle tanımlamak alışılagelmiştir. Bu demek oluyor ki:

${\displaystyle W=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {x} =\int _{\mathbf {x} (t_{1})}^{\mathbf {x} (t_{2})}\mathbf {F} \cdot \mathrm {d} \mathbf {x} =U(\mathbf {x} (t_{1}))-U(\mathbf {x} (t_{2})).}$

U(x) fonksiyonu uygulanan güçle bağdaştırılan potansiyel enerji olarak adlandırılır. Yerçekimi ve yay kuvvetleri potansiyel enerjisi olan kuvvetlere örnektir. Bu durumda, işin gradyanı şu sonucu verir;

${\displaystyle {\frac {\partial W}{\partial \mathbf {x} }}=-{\frac {\partial U}{\partial \mathbf {x} }}=-{\big (}{\frac {\partial U}{\partial x}},{\frac {\partial U}{\partial y}},{\frac {\partial U}{\partial z}}{\big )}=\mathbf {F} ,}$

ve F kuvveti “potansiyelden türetilebilir” denir.

Yer Çekimi Tarafından Yapılan İş

Gravity F=mg does work W=mgh along any descending path

Yerçekimi her nesne üzerine devamlı aşağıya doğru bir kuvvet uygular. Yeryüzünün yüzeyine yakın yerlerde yerçekimine bağlı ivme g=9.8 m.s⁻² ‘dir ve m kütleli nesnenin üzerindeki yerçekimi kuvveti F_g=mg’dır. Bu yerçekimi kuvvetini nesnenin kütle merkezine yoğunlaşmış olarak düşünmek gerekir. Eğer bir nesnenein y₂ - y₁ dikey uzaklığında yukarıya ya da aşağıya doğru yeri değiştirilirse, mg cinsinden ağırlığı tarafından nesneye yapılan W işi:

${\displaystyle W=F_{g}(y_{2}-y_{1})=F_{g}\Delta y=mg\Delta y}$

F_g (İngiliz ölçü birimde pound, SI birimlerinde Newton) ağırlık ve Δy, y yüksekliğindeki değişim. Yerçekimi tarafından yapılan işin yalnızca nesnenin dikey hareketine dayandığına dikkat edin. Sürtünmenin varlığı nesneye ağırlığı tarafından yapılan işi etkilemez.

Uzayda Kütleçekimi Tarafından Yapılan İş

m kütlesi üzerindeki diğer bir M kütlesi tarafına uygulanan yerçekimi kuvveti şu şekilde verilmiştir:

${\displaystyle \mathbf {F} =-{\frac {GMm}{r^{3}}}\mathbf {r} ,}$

r vektörün M ’den m’ye olan konumu.

m kütlesini v süratinde hareket ettirin, r(t₁) konumundan r(t₂) konumuna hareket ederken kütle üzerindeki yerçekiminin yaptığı iş şu şekilde olur:

${\displaystyle W=-\int _{\mathbf {r} (t_{1})}^{\mathbf {r} (t_{2})}{\frac {GMm}{r^{3}}}\mathbf {r} \cdot d\mathbf {r} =-\int _{t_{1}}^{t_{2}}{\frac {GMm}{r^{3}}}\mathbf {r} \cdot \mathbf {v} dt.}$

m kütlesinin süratinin ve konumunun şu şekilde olduğuna dikkat edin:

${\displaystyle \mathbf {r} =r\mathbf {e} _{r},\qquad \mathbf {v} ={\dot {r}}\mathbf {e} _{r}+r{\dot {\theta }}\mathbf {e} _{t},}$

e_r ve e_tM’den m’ye olan vektöre ilişkin yönlendirilen radyal ve teğetsel vektörlerdir. Bunu yerçekiminin yaptığı işin formülünü sadeleştirmede kullanın,

${\displaystyle W=-\int _{t_{1}}^{t_{2}}{\frac {GmM}{r^{3}}}(r\mathbf {e} _{r})\cdot ({\dot {r}}\mathbf {e} _{r}+r{\dot {\theta }}\mathbf {e} _{t})dt=-\int _{t_{1}}^{t_{2}}{\frac {GmM}{r^{3}}}r{\dot {r}}dt={\frac {GMm}{r(t_{2})}}-{\frac {GMm}{r(t_{1})}}.}$

Bu hesaplama

${\displaystyle {\frac {d}{dt}}r^{-1}=-r^{-2}{\dot {r}}=-{\frac {\dot {r}}{r^{2}}}.}$ kullanılır.

Bu fonksiyon

${\displaystyle U=-{\frac {GMm}{r}},}$

yerçekiminin potansiyel enerjisi olarak da bilinen, yerçekiminin potansiyel fonksiyonudur. Negatif işaret bir potansiyel enerji kaybından işin kazanıldığı düzeni takip eder.

Yay Tarafından Yapılan İş

Forces in springs assembled in parallel

Yaylardaki kuvvetler paraleldir.Bir nesnenin nasıl hareket ettiğinden bağımsız olarak x yönündeki sapmasına orantısal olan bir yatay F=(-kx, 0, 0) kuvveti uygulayan bir yay göz önüne alın. Bu yayın X(t) = (x(t), y(t), z(t)), eğrisi boyunca hareket eden bir nesne üzerindeki işi F sağlamak için v=(v_x, v_y, v_z), sürati kullanılarak hesaplanır.^[]

Kolaylık için, t=0 noktasında yayla oluşan teması dikkate alın, x mesafesindeki sonucun integrali ve sonra da xv_x, is (1/2)x²

Gaz Tarafından Yapılan İş

${\displaystyle W=\int _{a}^{b}{-P}dV}$

P basınç, V hacim, a ve b ise önceki ve en son hacimler.

İş-Enerji İlkesi

İş ve kinetik enerji ilkesi (iş-enerji ilkesi olarak da bilinir) bir parçacık üzerine etki eden bütün kuvvetler tarafından yapılan işin parçacığın kinetik enerjisindeki değişime eşit olduğunu öne sürer.

Bir parçacık üzerine bileşke kuvvet tarafından yapılan W işi parçacığın kinetik enerjisindeki ${\displaystyle E_{k}}$, F değişime eşittir:

${\displaystyle W=\Delta E_{k}={\tfrac {1}{2}}mv_{2}^{2}-{\tfrac {1}{2}}mv_{1}^{2}}$,

${\displaystyle v_{1}}$ ve ${\displaystyle v_{2}}$ parçacığın değişim öncesi ve sonrasındaki hızları ve m kütle.

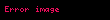
Eğer bileşke dönme momenti katı bir cisim üzerine etki ederse, tanım bileşke tork tarafından yapılan iş ve katı cismin rotasyonal kinetik enerjisindeki değişimi eşitlemek için genişletilebilir.

Genel Bakış

İş-enerji ilkesinin açığa çıkışı Newton’un ikinci kuralı ile ve parçacığa uygulanan kuvvetleri de içeren bileşke kuvvet ve hareketini etkileyen sınırlayıcı kuvvetlerle başlar. Parçacığın sürati ile birlikte kuvvetlerin skaler çarpımlarının ölçümlemesi sisteme eklenen eni gücü değerlendirir. Sınırlayıcılar parçacığın hareket yönünü sınırlayıcı kuvvetin yönünde süratin bileşkesi olmamasını sağlayarak belirlerler. Bu aynı zamanda sınırlayıcı kuvvetlerin ani güce katılmadıkları anlamına gelir. Bu skaler denklemin zamana göre türevi ani güçten iş ve sürat ve ivmenin skaler çarpımından kinetik enerji kazancı sağlar. İş-enerji ilkesinin sınırlayıcı kuvvetleri ortadan kaldırdığı gerçeği Lagrange mekaniği altında yatar. Bu bölüm iş-enerji ilkesine parçacık dinamiğine uygulanması noktasında odaklanıyor. Daha genel sistemlerde iş bir mekanik aracın potansiyel enerjisini, termal sistemdeki ısı enerjisini ya da bir elektronik aygıttaki elektrik enerjisini değiştirebilir. İş enerjisi bir noktadan diğerine ya da bir formdan diğerine transfer eder.

Düz bir hatta hareket eden parçacığın için türev

F bileşke kuvvet'in genlik ve yönde sabit olması ve parçacığın süratine paralel olması durumunda parçacık düz bir hat boyunca sabit bir ivme ile hareket eder. Net kuvvet ve içme arasındaki ilişki F = ma(Newton’un ikinci kuralı) denklemiyle verilir ve s parçacık yerdeğişimi aşağıdaki denklemle ifade edilebilir:

${\displaystyle s={\frac {v_{2}^{2}-v_{1}^{2}}{2a}}}$

${\displaystyle v_{2}^{2}=v_{1}^{2}+2as}$ sonucu çıkar.

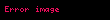
Net kuvvetin yaptığı iş genliğin ve parçacık yerdeğişiminin çarpımı olarak hesaplanır. Yukarıdaki denklemlere alternatif olarak:

${\displaystyle W=Fs=mas=ma\left({\frac {v_{2}^{2}-v_{1}^{2}}{2a}}\right)={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^{2}}{2}}=\Delta {E_{k}}}$

Doğrusual hareket durumunda genelde, F net kuvveti yönde sabit fakat genlikte sabit olmadığında ve sürate paralel olduğunda, iş parçacığın yolu boyunca birleştirilmiş olmalıdır:

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=\int _{t_{1}}^{t_{2}}F\,vdt=\int _{t_{1}}^{t_{2}}ma\,vdt=m\int _{t_{1}}^{t_{2}}v\,{dv \over dt}\,dt=m\int _{v_{1}}^{v_{2}}v\,dv={\tfrac {1}{2}}m(v_{2}^{2}-v_{1}^{2}).}$

Bir parçacık için iş-enerji teoreminin genel türevi

Eğrisel bir yol boyu hareket eden bir parçacık üzerine etki eden bir net kuvvet için, kuvvetinin parçacığın kinetik enerjisindeki değişime eşit olduğu yukarıdaki denkleme basit bir türev analoguyla gösterilebilir. Bazı yazarlar bu sonuca iş enerji ilkesi der fakat yaygın olarak iş enerji teoremi olarak bilinir:

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=m\int _{t_{1}}^{t_{2}}\mathbf {a} \cdot \mathbf {v} dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {dv^{2}}{dt}}\,dt={\frac {m}{2}}\int _{v_{1}^{2}}^{v_{2}^{2}}dv^{2}={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^{2}}{2}}=\Delta {E_{k}}}$

${\displaystyle \textstyle \mathbf {a} \cdot \mathbf {v} ={\frac {1}{2}}{\frac {dv^{2}}{dt}}}$ özdeşliği biraz cebir gerektirir. ${\displaystyle \textstyle v^{2}=\mathbf {v} \cdot \mathbf {v} }$ özdeşliğinden ve ${\displaystyle \textstyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}}$ tanımından şu sonuç ortaya çıkar:

${\displaystyle {\frac {dv^{2}}{dt}}={\frac {d(\mathbf {v} \cdot \mathbf {v} )}{dt}}={\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} +\mathbf {v} \cdot {\frac {d\mathbf {v} }{dt}}=2{\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} =2\mathbf {a} \cdot \mathbf {v} }$.

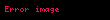
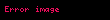
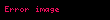
Yukarıdaki türevin kalan kısmı sadece önceki doğrusal durumda olduğu gibi basit matematiktir.

Sınırlanmış hareketteki bir parçacık için türev

Parçacık dinamiğinde, bir sisteme uygulanan işi kinetik enerjisindeki değişime eşitleyen bir formül Newton’un ikinci hareket yasasının ilk integrali olarak sağlanır. Newton’un yasalarında kullanılan bileşke kuvvet'in parçacığa uygulanan kuvvetler ve parçacığın hareketindeki sınırlayıcılara maruz kalan kuvvetler olarak ayrılabileceğini fark etmek gerekir. Sınırlayıcı kuvvetin işi sıfırdır, dolayısıyla yalnızca kuvvetlere uygulanan işin iş-enerji ilkesinde değerlendirilmesi gerekir.

Bunu görmek için, P parçacığının X(t) gidim izini üzerine etki eden F kuvvetiyle takip ettiğini göz önüne alın. Parçacığı Rsınırlayıcı kuvveti uygulamak için ortamından ayırın, o zaman Newton yasaları

${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }},}$ Formunu alır.

m parçacık kütlesi.

Vektör formülasyonu

Bir vektörün üzerindeki noktaların onun zamana göre n’inci türevini gösterdiğine dikkat edin. Sürat vektörü ile birlikte Newton’un yasalarının her iki yanının skaler çarpımı da

${\displaystyle \mathbf {F} \cdot {\dot {\mathbf {X} }}=m{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }},}$ sonucunu verir.

Çünkü sınırlayıcı kuvvetler parçacık süratine dikeydir. Bu denklemi X(t₁) noktasından X(t₂) noktasına olan gidişatı boyunca

${\displaystyle \int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\dot {\mathbf {X} }}dt=m\int _{t_{1}}^{t_{2}}{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}dt.}$ elde etmek için integralini alın.

Bu denklemin sol tarafı t₁ zamanından t₂ zamanına kadar olan gidişatı boyunca paracık üzerine etki ederken uygulanan kuvvetin yaptığı iştir. Bu aynı zamanda

${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\dot {\mathbf {X} }}dt=\int _{\mathbf {X} (t_{1})}^{\mathbf {X} (t_{2})}\mathbf {F} \cdot d\mathbf {X} .}$ olarak da yazılabilir.

Bu integral parçacığın X(t) gidim izi boyunca hesaplanmış ve dolayısıyla bağımlı opsiyondur. Newton’un denklemlerinin ilk integralinin sağ kısmı aşağıdaki ifade kullanılarak sadeleştirilebilir:

${\displaystyle {\frac {1}{2}}{\frac {d}{dt}}({\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }})={\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }},}$

Şimdi kinetik enerjideki değişimi elde etmek için açıkça integrali alınmış oldu,

${\displaystyle \Delta K=m\int _{t_{1}}^{t_{2}}{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {d}{dt}}({\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }})dt={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}(t_{2})-{\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}(t_{1})={\frac {1}{2}}m\Delta \mathbf {v^{2}} ,}$

parçacığın kinetik enerjisi skaler büyüklük olarak tanımlanmıştır.

${\displaystyle K={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}={\frac {1}{2}}m{\mathbf {v^{2}} }}$

Teğetsel ve normal bileşenler

Sürat ve ivme vektörlerini X(t) gidim izi boyunca teğetsel ve normal bileşenlerine şu şekilde ayırmak faydalı olacaktır:

${\displaystyle {\dot {\mathbf {X} }}=v\mathbf {T} ,\quad {\mbox{and}}\quad {\ddot {\mathbf {X} }}={\dot {v}}\mathbf {T} +v^{2}\kappa \mathbf {N} .}$

${\displaystyle v=|{\dot {\mathbf {X} }}|={\sqrt {{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}}}.}$

Bu durumda, Newton’un ikinci yasasında ivmeyle süratin skaler çarpımı

${\displaystyle \Delta K=m\int _{t_{1}}^{t_{2}}{\dot {v}}vdt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {d}{dt}}v^{2}dt={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}),}$. formunu alır.

Parçacığın kinetik enerjisi skaler büyüklük olarak tanımlanmış.

${\displaystyle K={\frac {m}{2}}v^{2}={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}.}$

Sonuç parçacık dinamiği için iş-enerji ilkesidir.

${\displaystyle W=\Delta K.\!}$

Bu türev rastlantısal katı cisim sistemlerine genellenebilir.

Düz bir hatta hareket (kayarak durma)

F toplamını veren bir itme kuvveti ve yerçekimi kuvveti etkisi altında bir düz yatay gidim izi boyunca hareket eden bir aracı düşünün. Araç ve yol arasındaki sınırlayıcı kuvvetler R olarak tanımlanır ve

${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }}.}$ elde ederiz.

Kolaylık için, gidim izini X ekseni boyunca alın böyleceX=(d,0) ve sürat V=(v, 0) olur, dolayısıyla da R.V=0 ve and F.V=F_xv (F_x x ekseni boyunca F’in bileşeni) olur. Yani,

${\displaystyle F_{x}v=m{\dot {v}}v.}$

İki tarafın integrali

${\displaystyle \int _{t_{1}}^{t_{2}}F_{x}vdt={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}).}$ sonucunu verir.

Eğer F_x gidişat boyunca sabit ise o zaman sürat integrali mesafedir, yani

${\displaystyle F_{x}(d(t_{2})-d(t_{1}))={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}).}$

Örnek olarak kayarak duran bir arabayı göz önüne alın (ksürtünme katsayısı ve W arabanın ağırlığı). Bu durumda gidim izi boyunca kuvvet F_x =-kW olur. Arabanın sürati v iş-enerji ilkesi kullanılarak kaymanın s uzunluğundan belirlenebilir.

${\displaystyle kWs={\frac {W}{2g}}v^{2},\quad {\mbox{or}}\quad v={\sqrt {2ksg}}.}$

Bu formülün aracın kütlesinin m=W/g olduğu gerçeğini kullandığına dikkat edin.

Lotus type 119B gravity racer at Lotus 60th celebration.

Gravity racing championship in Campos Novos, Santa Catarina, Brazil, 8 September 2010.

Bir dağ yolundan aşağıya inme

Bir aracın hareketsiz olarak başladığı ve bir dağ yolundan aşağıya doğru gittiğini düşünün, iş-enerji ilkesi aracın Vsüratine ulaşmak için gittiği minimum mesafeyi hesaplamaya yardım eder. Yuvarlanma direnci ve hava direnci aracı yavaşlatacaktır yani asıl mesafe kuvvetler ihmal edildiği durumdan daha az olacaktır.

Yolu takip eden aracın gidim izinin üç boyutlu uzayda bir eğim olan X(t) olarak alın. Araç üzerine etkiyen ve onu aşağıya doğru iten kuvvet sabit yerçekimi kuvvetiyken, yolun araç üzerindeki kuvveti X(t) sınırlayıcı kuvvetidir. Newton’un ikinci yasası

${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }}.}$ sonucunu verir.

Bu denklemin V=(v_x, v_y,v_z) vektörüyle sakler çarpımı :${\displaystyle Wv_{z}=m{\dot {V}}V,}$ sonucunu verir. V V’nin genliği. Araç ve yol arasındaki sınırlayıcı kuvvetler bu denklemi geçersiz kılar çünküR.V=0 ve bu iş yapmadıkları anlamına gelir. İki tarafın da :${\displaystyle \int _{t_{1}}^{t_{2}}Wv_{z}dt={\frac {m}{2}}V^{2}(t_{2})-{\frac {m}{2}}V^{2}(t_{1}).}$ elde etmek için integralini alalım.

W ağırlık kuvveti gidim izi boyunca sabittir ve dikey süratin integrali dikey uzaklıktır, yani,

${\displaystyle W\Delta z={\frac {m}{2}}V^{2}.}$

V(t₁)=0 olduğunu hatırlayın. Bu sonucun araç tarafından gidilen yolun şekline bağlı olmadığına dikkat edin. Yol boyu uzaklığı belirlemek için eğimin %6 yani dik bir yol olduğunu varsayalım. Bu –açılar için sin ve tan fonksiyonları neredeyse eşit- rakım her 100 fitte 6 fit azalıyor demektir. Dolayısıyla, %6 eğimli bir yolda V süratine ulaşmak için s mesafesi en azından

${\displaystyle s={\frac {\Delta z}{0.06}}=8.3{\frac {V^{2}}{g}},\quad {\mbox{or}}\quad s=8.3{\frac {88^{2}}{32.2}}\approx 2000{\mbox{ft}}.}$ dir.

Bu formül aracın ağırlığının W=mg olduğu gerçeğini kullanmıştır.

Katı bir cisim üzerine etkiyen kuvvetlerin yaptığı iş

Tek bir katı cisim üzerine çeşitli noktalardan etki eden kuvvetlerin yaptığı iş bileşke kuvvet ve tork'un işinden hesaplanabilir.^[] Bunu görmek için F₁,F₂ ... F_n kuvvetlerini bir katı cisme X₁, X₂ ... X_n noktalarından uygulayalım. X_i, i=1,...,n gidim izleri katı cismin hareket tarafından tanımlanır. Bu hareket [A(t)] rotasyonlar seti ve cisim üzerindeki referans noktanın d(t) gidim izi tarafından verilir.x_i i=1,...,n koordinatları hareket eden cismin M referans çerçevesi içindeki bu noktaları tanımlasın. Böylece F sabit çerçevesindeki izlenen gidim izleri şu şekilde verilir:

${\displaystyle \mathbf {X} _{i}(t)=[A(t)]\mathbf {x} _{i}+\mathbf {d} (t)\quad i=1,\ldots ,n.}$

Gidişatları boyunca X_i noktalarının süratleri

${\displaystyle \mathbf {V} _{i}={\vec {\omega }}\times (\mathbf {X} _{i}-\mathbf {d} )+{\dot {\mathbf {d} }},}$

ωters simetrik matriksten elde edilen açısal sürat vektörüdür. Açısal sürat matriksi olarak bilinir.^[]

Küçük δr_i yer değişimleri üzerindeki kuvvetler tarafından yapılan az miktarda iş yaklaşık olarak δr=vδt yerdağişimi tarafından belirlenebilir.^[]

${\displaystyle \delta W=\mathbf {F} _{1}\cdot \mathbf {V} _{1}\delta t+\mathbf {F} _{2}\cdot \mathbf {V} _{2}\delta t+\ldots +\mathbf {F} _{n}\cdot \mathbf {V} _{n}\delta t}$

Ya da

${\displaystyle \delta W=\sum _{i=1}^{n}\mathbf {F} _{i}\cdot ({\vec {\omega }}\times (\mathbf {X} _{i}-\mathbf {d} )+{\dot {\mathbf {d} }})\delta t.}$

Bu formül

${\displaystyle \delta W=(\sum _{i=1}^{n}\mathbf {F} _{i})\cdot {\dot {\mathbf {d} }}\delta t+(\sum _{i=1}^{n}(\mathbf {X} _{i}-\mathbf {d} )\times \mathbf {F} _{i})\cdot {\vec {\omega }}\delta t=(\mathbf {F} \cdot {\dot {\mathbf {d} }}+\mathbf {T} \cdot {\vec {\omega }})\delta t,}$ elde etmek için bu şekilde tekrar yazılabilir.

F ve T katı cismin M hareket çerçevesindeki d referans noktasına uygulanan bileşke kuvvet ve dönme momentinin sonuçlarıdır.^[]

Kaynakça

1. ^ ^{a b} Hugh D. Young and Roger A. Freedman (2008). University Physics. 12th. Addison-Wesley. s. 329. ISBN . 

Dış bağlantılar

• İngilizce vikipedi24 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi.