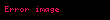Boyut analizi fiziksel büyüklüklerin farklı çeşitlerinin karışımını içeren fiziksel durumları içeren ve sıklıkla fizik, kimya ve mühendislikte kullanılan kavramsal bir yöntemdir.Fizikçiler ve mühendisler tarafından türevli denklemlerin ve hesaplamaların olasılıklarının kontrolünde kullanılır.Ayrıca deneylerle veya kavramın daha karmaşık teorileriyle denenebilen karmaşık fiziksel durumlarla ilgili mantıklı hipotezler oluşturmak için de kullanılır.
Giriş
Bir fiziksel büyüklüğün boyutları M kütle, L uzunluk ve T zaman ile bağlatılıdır, bunların her biri de kuvvetleriyle orantılı olarak artar.Örneğin; fiziksel bir büyüklük olan hızın boyutu "uzunluk/zaman"dır (L/T) ve kuvvetin de boyutu "kütle×ivme" veya "kütle×(uzunluk/zaman)/zaman"dır (ML/T2).
Fiziksel bir büyüklüğün birimi ile boyutu birbirleri ile bağlantılıdır fakat kesin tanımlayıcı kavramlar değillerdir.Fiziksel bir büyüklüğün birimleri geleneksel olarak tanımlanır ve bazı standartlarla ilişkilidir; örneğin uzunluğun birimi metre, feet, inch veya mikrometre olabilir; fakat herhangi bir uzunluk, onu ölçmek için keyfi olarak seçilen birimden bağımsız olarak daima L boyutuna sahiptir.Aynı fiziksel büyüklüğün iki farklı birimi çeşitli dönüştürme faktörleriyle birbirlerine dönüştürülebilirler.Örneğin; 1 inç = 2.54 cm; böylece (2.54 cm/in) dönüşüm faktörü olarak adlandırılır (yaygın bir büyüklüğün farklı birimleriyle gösterimlerinin arasındaki dönüşümü yapar) ve boyutsuzdur ve bire eşittir.Boyut sembolleri arasında dönüşüm faktörleri yoktur.
Boyut sembolleri, L gibi, matematiksel bir grup oluştururlar: buna göre şu özdeşlik yazılabilir, L0=1; Lnin tersi ise, ki bu 1/L veya L−1dir ve L'nin tüm oransal p kuvvetleri grubun bir üyesidir, tersi için de aynı şey geçerlidir L-p or 1/Lp.Grubun işlemi çarpımdır ve standart üslü işlemler uygulanır(Ln × Lm = Ln+m).
Mekanikte, herhangi bir fiziksel büyüklüğün boyutu M, L ve T tabanlı terimlerle ifade edilebilir.Bu tek mümkün seçenek değildir, fakat en sık kullanılanıdır.Örneğin, bazıları kuvvet F, uzunluk L ve kütle M boyutlarını temel almaktadırlar.Bu sebepten temel boyutların seçimi kısmen gelenekle ilgilidir ve kullanışlılığı ve aşinalığı arttırır.Bununla birlikte boyutların seçiminin sadece bir gelenek olmadığını da fark etmek önemlidir; örneğin, uzunluğu, hızı ve zamanı temel boyut olarak kullanmak iyi bir seçim deildir; çünkü mass—'i elde etmenin; veya force— gibi, ondan türetilen hiçbir şeyi başka bir temel boyut eklemeden elde etmenin yolu yoktur ve hız uzunluk ve zamandan türetilebildiğinden bu temel boyutlar en iyi anlatımla tam kullanılmaz ve en kötüsü de uygunsuzdur(örneğin eğer hızın temel birimi uzunluğun temel biriminin zamanın temel birimine oranı olan 1'e eşit değilse).
Kolaylık açısından tüm bilim dünyasının aynı seçimleri yapması önemlidir.SI birim sistemi en geniş kullanılan birimdir ve gerekli şekilde karmaşadan ve çakışmadan çeşitli birim dönüşümleri ile sakınır (santimetre gram saniye birim sistemi).
Fizik alanına bağlı olarak, boyut sembol setlerinden biri veya öbürünü seçmek avantajlı olabilir.Örneğin elektromagnetizmada M, L, T ve elektriksel yükü temsil eden Q boyutları kullanışlı olacaktır.Termodinamikte ise temel boyut setine sık sık sıcaklık için bir boyut eklenir.Kimyada moleküllerin sayısı da hesaba katılır ve bunun için bir boyut kullanılması da kullanışlı olur.Fiziğin farklı alanlarında kullanılacak boyutların veya hatta boyut sayısının seçimi daha çok keyfi olsa da kullanımdaki uyum ve iletişimdeki kolaylık en önemli husustur.
En ilkel formunda, boyut analizi fiziksel eşitliklerin olasılıklarını kontrol etmede kullanılabilir: herhangi bir eşitliğin iki tarafı da aynı ölçekte veya aynı boyutta olmalıdır, yani, eşitlik boyutsal olarak homojen olmalıdır.Bu gerekliliğin doğal bir sonucu olarak, fiziksel olarak anlamlı bir eşitlikte sadece aynı boyuttaki büyüklükler toplanabilir veya çıkarılabilir.Örneğin bir fare ile bir pirenin kütleleri birbirlerine eklenebilse de pirenin kütlesi ile farenin boyu anlamlı şekilde birbirine eklenemez.Farklı boyutlara sahip fiziksel büyüklükler birbirleriyle karşılaştırılamazlar da.Örneğin, "3 m > 1 g" anlamlı bir ifade değildir.
Sadece aynı boyuttaki büyüklükler toplanabilir, çıkarılabilir, karşılaştırılabilir veya eşitlenebilir.Farklı boyutlu büyüklükler "+", "-" ve "=" işaretlerinin tersi olarak görüldüğünde, o fiziksel eşitlik mümkün değildir, bunu kullanmadan önce hatalar düzeltilmelidir.Aynı veya farklı boyutlu büyüklükler çarpıldığında veya bölündüğünde, onların boyutsal sembolleri de çarpılır veya bölünür.Boyutlu büyüklüklerin üsleri alındığında ise aynı şey bunlara eklenen boyutsal sembollere de yapılır.
Üslü fonksiyonların, trigonometrik fonksiyonların, logaritmik ve diğer transandantal fonksiyonların skaler değişkenleri de boyutsuz olmalıdır.Bu gereklilik bu fonksiyonların Taylor açılımı alındığında açıklık kazanır.Örneğin, 3'ün logaritması neredeyse 0,477 iken 3 kg'ın logaritması tanımsızdır.ln3kg gibi bir hesap ise şu sonucu üretecektir
bu ise boyutsal olarak uyumsuzdur.
Boyutsal fiziksel bir büyüklüğün değeri onun biriminin ve boyutlu ve boyutsuz sayısal faktörlerin çarpımı şeklinde yazılır.Tam olarak, benzer boyutlu büyüklükler toplandığında, çıkarıldığında veya karşılaştırıldığında, bu boyutlu büyüklükler, sayısal büyüklükleri doğrudan toplanabilsin veya çıkarılabilsin diye, uyumlu birimlerle ifade edilmelidirler.Fakat, kavramsal olarak, farklı birimlerle ifade edilen aynı boyutlu büyüklükleri toplamada bir sorun yoktur.Örneğin, 1 metre 1 feet'e eklendiğinde bir uzunluk elde ederiz, fakat sonucu elde etmek için 1'e 1 eklemek yanlış olacaktır.Aynı boyutlu büyüklüklerin bir oranı olan ve boyutsuz bir sayıya eşit olan bir dönüşüm faktörüne gereksinim duyulur:
veya
Buradaki faktör 
Sadece bu yolla farklı birimlerdeki büyüklükler birbirleriyle toplanabilirler.
Boyut analizi ayrıca birinin anlamak ve karakterize etmek istediği özel kavramların içinde bulunan fiziksel büyüklüklerin arasındaki ilişkileri türetmekte kullanılır.İlk kez 1872 yılında, gökyüzünün neden mavi olduğunu anlamaya çalışan Lord Rayleigh tarafından kullanılmıştır.
Basit bir örnek
Yerçekimi kuvveti 












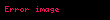
Analizimizin durumun fiziksel tanımına ait olduğuna emin olduğumuz bir değişkeni reddetmesi ile karşılaştığımızda(burada g), reddedilen değişkenin durumla alakalı olduğunu ve bizim durumla alakalı başka değişkenleri, reddedilen değişkenle beraber bir kombinasyonla boyutsuz bir büyüklük oluşturabilecek, sildiğimiz ihtimalini düşünebiliriz.Ancak burada durum o şekilde değildir.
Sadece kuvetlerin bir boyutsuz çarpımını içeren problemlerde boyut analizi ile sonuca ulaştığımızda, burada olduğu gibi, bilinmeyen fonksiyon yoktur ve çözüm "tamam"dır denir.
Daha karmaşık bir örnek
l [





burada F bilinmeyen bir fonksiyondur, veya, eşit şekilde
burada f bilinmeyen başka bir fonksiyondur.Burada bilinmeyen fonksiyon çözümümüzün tamamlanmadığı anlamına gelir, fakat boyut analizi bize açık olmayan bazı şeylerde vermişti:Enerji gerilmenin ilk kuvvetiyle orantılıdır.Daha ileri analitik analiz haricinde, bilinmeyen f fonksiyonunu bulmak için deney de yapabiliriz.Fakat deney yapmak eğer boyut analizi mümkün değilse daha kolaydır.Enerjinin gerilmeyle orantılı olduğunu kanıtlamak için hiçbir şey yapamazdık. Veya belki enerjinin 

Yukarıdakilere benzemeyen, daha kompleks, içerdiği değişkenlerin belirsiz olduğu ve temel denklemlerinin umutsuzca karmaşık olduğu durumlara uygulandığında; boyut analizinin gücü gerçekten belirginleşir.Örneğin, bir nehir yatağındaki küçük bir çakıl taşını düşünelim.Eğer nehir yeterince hızlı akıyorsa, çakıltaşı yükselir ve su içinde yüzer.Peki kritik hız nedir?Tahmin edilen değişkenleri çözmek daha öncekiler kadar kolay değildir.Fakat boyut analizi bunun gibi problemleri anlamakta yardımcı olabilir ve temel denklemlerin zr anlaşıldığı, karmaşık problemlerde uygulanacak ilk elemandır.
Huntley toplamı
Huntley (Huntley, 1967) boyut kavramımızı zaman zaman rafine etmemizin verimli olacağını iddia etmiştir.İki olası rafinasyon şunlardır:
- Bir vektörün bileşenlerinin büyüklüklerinin boyutsal olarak farklı olduğu düşünülmelidir.Örneğin, For example, farklılaştırılmamış bir uzunluk birimi L'dense,
gibi x yönün deki uzunluğu gösteren bir boyutu kullanabiliriz, diğer yönlerde de bu geçerlidir.Bu gereklilik temel olarak, fiziksel olarak anlamlı bir denklemin her bir bileşeninin(skaler, vektör veya tensör) boyutsal olarak uyumlu olması gerekliliğine dayanır.
- Bir büyüklük ölçüsü olarak kütle, bir atalet ölçüsü olan kütleden boyutsal olarak farklı düşünülmelidir.
İlk rafinasyonun kullanışlılığının bir örneği olarak, dikey 





Bu dört büyüklükle, R menzille ilgili aşağıdaki denkleme ulaşabiliriz:
veya boyutsal olarak
buradan bir katsayıyı tanımsız bırakan 

Bununla birlikte eğer yönlü uzunluk boyutlarını kullanırsak, o zaman 





ve şu sonuca varırız 


Benzer şekilde, ataletsel kütle ile maddesel kütleyi birbirinden ayırmak(örneğin akışkanlar mekaniği ve termodinamikte) zaman zaman kullanışlı bulunabilir.Örneğin, Poiseuille Yasası'nın türetilmesini düşünelim.Silindirik bir boru içinde viskoz bir akışkanın kütle akış oranını bulmak istiyoruz.Eğer ataletsel ve maddesel kütleyi birbirinden ayırmazsak ilgili şu değişkenleri seçebiliriz
;
boyutlu kütle akış oranı
;
boyutlu boru boyunca basınç gradyanı
;
boyutlu yoğunluk
;
boyutlu dinamik akışkan viskozitesi
;
boyutlu boru yarıçapı
Üç temel değişken vardır bu yüzden yukarıdaki beş eşitlik iki boyutsuz değişkene uyum sağlar; 

burada C ve a belirsiz sabitlerdir.Eğer ataletsel kütle(boyutu 

burada C belirsiz sabittir (boyut analizi dışındaki metotlarla 
Engelleri ve Geliştirilmesi: Yönelimsel çözümleme
Huntley toplamının bazı ciddi engelleri vardır.Ne çapraz çarpım içeren vektör denklemleri ile uğraşır ve ne de açıları fiziksel değişkenler olarak iyi şekilde kullanır.Ayrıca genellikle ilgilenilen problemlerde L'yi, 


Açılar geleneksel olarak boyutsuz değişkenler olarak düşünülmektedirler ve bu yüzden boyut analizinde açıların fiziksel değişken olarak kullanımı daha az anlamlı sonuçlar verir.Örneğin, yukarıdaki top örneğini düşünelim.Düşünün ki, x- ve y- ilk hız bileşenleri yerine, hızın büyüklüğü v ve fırlatılış açısı 
Siano (Siano, 1985-I, 1985-II) Huntley'in yönlü boyutlarının, vektörlerin yönlerini ve yönelimsiz sembol 





Yönelimsel sembollerin matematiksel grup oluşturduğuna dikkat edin.Bu sistemde, skalerler, "problemin simetrisi"nden bağımsız olarak, daima aynı yönelimi tanımlayıcı eleman olarak bulundurur.Vektör olan fiziksel büyüklükler ise şu yönelimlere sahiptirler: x-yönlü bir kuvvetin veya hızın yönelimi 







Fiziksel büyüklüklerin yönelimsel sembollerinin görevleri ve fiziksel denklemlerin yönelimsel olarak homojen olma gereklilikleri gerçekte boyut analizine, fiziksel problemlerin kabul edilebilir çözümleri hakkında çok az bilgi türetme açısından benzerdir.Bu sebepten boyutsal denklemi kurduğumuzda ancak yapabildiğimiz kadarını çözeriz.Eğer bir fiziksel değişkenin en düşük kuvveti kesirli ise, çözümün her iki tarafı da tğm kuvvetlerin integrali alınmış gibi bir kuvvete yükselir. Bu da denklemi "normal form"'a getirir.Daha sonra yönelimsel denklem, yönelimsel sembollerin bilinmeyen kuvvetlerine daha kısıtlayıcı şartlar koymak için çözülür ve boyut analizinin tek başına verdiği sonuçtan daha tam bir sonuca ulaşılır. Sıklıkla, eklenen bilgi belli bir değişkenin kuvvetlerinden birinin tek mi çift mi olduğudur.
Örneğin, fırlatma probleminde, yönelimsel sembolleri kullanırsak, θ, x-y düzleminde olacaktır ve boyutu 
bunun anlamı şudur
Boyutsal homojenlik şimdi doğru şekilde a=-1 ve b=2'yi sağlar ve yönelimsel homojenlik c'nin bir tek tam sayı olmasını gerektirir.Aslında θ'nın gereksinilen fonksiyonu 

Yukarıdaki çarpım tablosunu kullandığımızda, 



Yönelimsel semboller için kullanılan çarpım kuralının iki vektörün çapraz çarpımı kuralıyla aynı olduğu açıktır.İki özdeş vektörün çapraz çarpımları sıfırdır, nitekim özdeş iki yönelimsel sembolün çarpımı da özdeş elemandır.
Felsefi temel
Sonuç olarak, boyut analizi ve fiziksel eşitliklerin boyutsal olarak homojen olması gerekliliği fizik kanunlarının fiziksel büyüklükleri ölçmekde kullanılan birimlerden bağımsız olduğu fikrini yansıtır.Yani, örneğin, eğer SI sistemi, İngiliz birim sistemi, cgs sistemi veya herhangi başka bir uygun birim sistemi kullanıldığında F = ma denklemi doğrudur.Yönelimsel analiz ve fiziksel denklemlerin yönelimsel olarak homojen olması gerekliliği de fizik denkleminin kullanılan koordinat sisteminden bağımsız olmasını gerektirdiği fikrini yansıtır.
Boyutsuz sabitler
Poiseuille'in kanunundaki C ve yukarıda tartışılan yay problemi ile ilgili 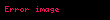
Buckingham π teoremi
boyut analizinin temelini oluşturan bir yöntemdir.Bu teorem n adet değişken içeren her anlamlı fiziksel denklemin n − m boyutsuz parametreli denklemle yeniden yazılabileceğini söyler, burada m kullanılan temel boyutların sayısıdır.Dahası ve daha önemlisi, teorem bu boyutsuz değişkenleri verilen değişkenlerden hesaplamak için bir yöntem sağlar.
Kaynakça
- Bhaskar, R. (1990). "Qualitative Physics Using Dimensional Analysis". Artificial Intelligence. Cilt 45. ss. 73-111.
- Bhaskar, R. (1991). "Qualitative Explanations of Red Giant Formation". The Astrophysical Journal. Cilt 372. ss. 592-6.
- Boucher (1960). "Dimensionless Numbers". Chem. Eng. Progress. Cilt 55. ss. 55-64.
- (1914). "On Physically Similar Systems: Illustrations of the Use of Dimensional Analysis". Phys. Rev. Cilt 4. s. 345.
- Klinkenberg, A. (1955), "Dimensional systems and systems of units in physics with special reference to chemical engineering: Part I. The principles according to which dimensional systems and systems of units are constructed", Chemical Engineering Science, 4 (3), ss. 130-140, 167-177, doi:10.1016/0009-2509(55)80004-8
- Moody, L. F. (1944). "Friction Factors for Pipe Flow". Trans. Am. Soc. Mech. Engrs. 66 (671).
- Murphy, N. F. (1949). "Dimensional Analysis". Bull. V.P.I. 42 (6).
- Perry, J. H. (1944). "Standard System of Nomenclature for Chemical Engineering Unit Operations". Trans. Am. Inst. Chem. Engrs. 40 (251).
- Petty, G. W. (2001). "Automated computation and consistency checking of physical dimensions and units in scientific programs". Software - Practice and Experience. Cilt 31. ss. 1067-1076.
- Lord Rayleigh (1915). "The Principle of Similitude". Nature. Cilt 95. ss. 66-68.
- Siano, Donald (1985). "Orientational Analysis - A Supplement to Dimensional Analysis - I". J. Franklin Institute, 320. s. 267.
- Siano, Donald (1985). "Orientational Analysis, Tensor Analysis and The Group Properties of the SI Supplementary Units - II". J. Franklin Institute, 320. s. 285.
- Silberberg, I. H. (1953). "Learning How to Use Dimensional Analysis". Petrol. Refiner. 32 (4 (p.5), 5(p.147), 6(p.101), 7(p.129)).
- Van Driest, E. R. (Mart 1946). "On Dimensional Analysis and the Presentation of Data in Fluid Flow Problems". J. App. Mech. 68 (A-34).
Dış bağlantılar
- http://en.wikibooks.org/wiki/Fluid_Mechanics/Ch4 8 Nisan 2009 tarihinde Wayback Machine sitesinde arşivlendi.
- Unicalc Live web calculator doing units conversion by dimensional analysis 22 Aralık 2008 tarihinde Wayback Machine sitesinde .
- http://www.math.ntnu.no/~hanche/notes/buckingham/buckingham-a4.pdf 20 Eylül 2008 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Boyut analizi fiziksel buyukluklerin farkli cesitlerinin karisimini iceren fiziksel durumlari iceren ve siklikla fizik kimya ve muhendislikte kullanilan kavramsal bir yontemdir Fizikciler ve muhendisler tarafindan turevli denklemlerin ve hesaplamalarin olasiliklarinin kontrolunde kullanilir Ayrica deneylerle veya kavramin daha karmasik teorileriyle denenebilen karmasik fiziksel durumlarla ilgili mantikli hipotezler olusturmak icin de kullanilir GirisBir fiziksel buyuklugun boyutlari M kutle L uzunluk ve T zaman ile baglatilidir bunlarin her biri de kuvvetleriyle orantili olarak artar Ornegin fiziksel bir buyukluk olan hizin boyutu uzunluk zaman dir L T ve kuvvetin de boyutu kutle ivme veya kutle uzunluk zaman zaman dir ML T2 Fiziksel bir buyuklugun birimi ile boyutu birbirleri ile baglantilidir fakat kesin tanimlayici kavramlar degillerdir Fiziksel bir buyuklugun birimleri geleneksel olarak tanimlanir ve bazi standartlarla iliskilidir ornegin uzunlugun birimi metre feet inch veya mikrometre olabilir fakat herhangi bir uzunluk onu olcmek icin keyfi olarak secilen birimden bagimsiz olarak daima L boyutuna sahiptir Ayni fiziksel buyuklugun iki farkli birimi cesitli donusturme faktorleriyle birbirlerine donusturulebilirler Ornegin 1 inc 2 54 cm boylece 2 54 cm in donusum faktoru olarak adlandirilir yaygin bir buyuklugun farkli birimleriyle gosterimlerinin arasindaki donusumu yapar ve boyutsuzdur ve bire esittir Boyut sembolleri arasinda donusum faktorleri yoktur Boyut sembolleri L gibi matematiksel bir grup olustururlar buna gore su ozdeslik yazilabilir L0 1 Lnin tersi ise ki bu 1 L veya L 1dir ve L nin tum oransal p kuvvetleri grubun bir uyesidir tersi icin de ayni sey gecerlidir L p or 1 Lp Grubun islemi carpimdir ve standart uslu islemler uygulanir Ln Lm Ln m Mekanikte herhangi bir fiziksel buyuklugun boyutu M L ve T tabanli terimlerle ifade edilebilir Bu tek mumkun secenek degildir fakat en sik kullanilanidir Ornegin bazilari kuvvet F uzunluk L ve kutle M boyutlarini temel almaktadirlar Bu sebepten temel boyutlarin secimi kismen gelenekle ilgilidir ve kullanisliligi ve asinaligi arttirir Bununla birlikte boyutlarin seciminin sadece bir gelenek olmadigini da fark etmek onemlidir ornegin uzunlugu hizi ve zamani temel boyut olarak kullanmak iyi bir secim deildir cunku mass i elde etmenin veya force gibi ondan turetilen hicbir seyi baska bir temel boyut eklemeden elde etmenin yolu yoktur ve hiz uzunluk ve zamandan turetilebildiginden bu temel boyutlar en iyi anlatimla tam kullanilmaz ve en kotusu de uygunsuzdur ornegin eger hizin temel birimi uzunlugun temel biriminin zamanin temel birimine orani olan 1 e esit degilse Kolaylik acisindan tum bilim dunyasinin ayni secimleri yapmasi onemlidir SI birim sistemi en genis kullanilan birimdir ve gerekli sekilde karmasadan ve cakismadan cesitli birim donusumleri ile sakinir santimetre gram saniye birim sistemi Fizik alanina bagli olarak boyut sembol setlerinden biri veya oburunu secmek avantajli olabilir Ornegin elektromagnetizmada M L T ve elektriksel yuku temsil eden Q boyutlari kullanisli olacaktir Termodinamikte ise temel boyut setine sik sik sicaklik icin bir boyut eklenir Kimyada molekullerin sayisi da hesaba katilir ve bunun icin bir boyut kullanilmasi da kullanisli olur Fizigin farkli alanlarinda kullanilacak boyutlarin veya hatta boyut sayisinin secimi daha cok keyfi olsa da kullanimdaki uyum ve iletisimdeki kolaylik en onemli husustur En ilkel formunda boyut analizi fiziksel esitliklerin olasiliklarini kontrol etmede kullanilabilir herhangi bir esitligin iki tarafi da ayni olcekte veya ayni boyutta olmalidir yani esitlik boyutsal olarak homojen olmalidir Bu gerekliligin dogal bir sonucu olarak fiziksel olarak anlamli bir esitlikte sadece ayni boyuttaki buyuklukler toplanabilir veya cikarilabilir Ornegin bir fare ile bir pirenin kutleleri birbirlerine eklenebilse de pirenin kutlesi ile farenin boyu anlamli sekilde birbirine eklenemez Farkli boyutlara sahip fiziksel buyuklukler birbirleriyle karsilastirilamazlar da Ornegin 3 m gt 1 g anlamli bir ifade degildir Sadece ayni boyuttaki buyuklukler toplanabilir cikarilabilir karsilastirilabilir veya esitlenebilir Farkli boyutlu buyuklukler ve isaretlerinin tersi olarak goruldugunde o fiziksel esitlik mumkun degildir bunu kullanmadan once hatalar duzeltilmelidir Ayni veya farkli boyutlu buyuklukler carpildiginda veya bolundugunde onlarin boyutsal sembolleri de carpilir veya bolunur Boyutlu buyukluklerin usleri alindiginda ise ayni sey bunlara eklenen boyutsal sembollere de yapilir Uslu fonksiyonlarin trigonometrik fonksiyonlarin logaritmik ve diger transandantal fonksiyonlarin skaler degiskenleri de boyutsuz olmalidir Bu gereklilik bu fonksiyonlarin Taylor acilimi alindiginda aciklik kazanir Ornegin 3 un logaritmasi neredeyse 0 477 iken 3 kg in logaritmasi tanimsizdir ln3kg gibi bir hesap ise su sonucu uretecektir 3kg 9kg22 displaystyle 3 mathrm kg frac 9 mathrm kg 2 2 cdots bu ise boyutsal olarak uyumsuzdur Boyutsal fiziksel bir buyuklugun degeri onun biriminin ve boyutlu ve boyutsuz sayisal faktorlerin carpimi seklinde yazilir Tam olarak benzer boyutlu buyuklukler toplandiginda cikarildiginda veya karsilastirildiginda bu boyutlu buyuklukler sayisal buyuklukleri dogrudan toplanabilsin veya cikarilabilsin diye uyumlu birimlerle ifade edilmelidirler Fakat kavramsal olarak farkli birimlerle ifade edilen ayni boyutlu buyuklukleri toplamada bir sorun yoktur Ornegin 1 metre 1 feet e eklendiginde bir uzunluk elde ederiz fakat sonucu elde etmek icin 1 e 1 eklemek yanlis olacaktir Ayni boyutlu buyukluklerin bir orani olan ve boyutsuz bir sayiya esit olan bir donusum faktorune gereksinim duyulur 1 ft 0 3048 m displaystyle 1 mbox ft 0 3048 mbox m veya 1 0 3048 m1 ft displaystyle 1 frac 0 3048 mbox m 1 mbox ft Buradaki faktor 0 3048 mft displaystyle 0 3048 frac mbox m mbox ft boyutsuz 1 e ozdestir boylece bu donusum faktorunu kullanarak carpim yapmak hicbir seyi degistirmez Ayni boyutta fakat farkli birimle ifade edilmis iki buyuklugu birbirine ekledigimizde aslinda 1 e esit olan uygun donusum faktoru buyukluklerin sayisal degerleri toplanabilsin veya cikarilabilsin diye birimleri ozdeslestirmek icin donusum yapmakta kullanilir 1 m 1 ft displaystyle 1 mbox m 1 mbox ft 1 m 1 ft 0 3048 mft displaystyle 1 mbox m 1 mbox ft times 0 3048 frac mbox m mbox ft 1 m 1 ft 0 3048 mft displaystyle 1 mbox m 1 mbox ft times 0 3048 frac mbox m mbox ft 1 m 0 3048 m displaystyle 1 mbox m 0 3048 mbox m 1 3048 m displaystyle 1 3048 mbox m Sadece bu yolla farkli birimlerdeki buyuklukler birbirleriyle toplanabilirler Boyut analizi ayrica birinin anlamak ve karakterize etmek istedigi ozel kavramlarin icinde bulunan fiziksel buyukluklerin arasindaki iliskileri turetmekte kullanilir Ilk kez 1872 yilinda gokyuzunun neden mavi oldugunu anlamaya calisan Lord Rayleigh tarafindan kullanilmistir Basit bir ornek Yercekimi kuvveti g displaystyle g dolayisiyla asili kalan k displaystyle k sabitli yaya bagli m displaystyle m kutlesinin saliniminin periyodu T displaystyle T nedir Bu dort buyuklugun boyutlari soyledir T displaystyle T T m displaystyle m M k displaystyle k M T 2 ve g displaystyle g L T 2 Buradan secilen degiskenlerin kuvvetlerinin carpimi olan boyutsuz tek bir sonuc elde ederiz G1 displaystyle G 1 T2k m displaystyle T 2 k m Degiskenlerin kuvvetlerinin carpimi olan bu boyutsuz sonuc bazen boyutsuz degisken grubu olarak adlandirilir fakat bu grup G1 displaystyle G 1 matematiksel bir grup olmaktan cok bir topluluk anlamindadir Sik sik boyutsuz sayilar olarak da adlandirilirlar g displaystyle g nin k m T ile veya sadece g ile kuvvetlerinin carpimlarini iceren baska boyutsuz carpimlarin olusturulamayacagina dikkat ediniz cunku g sadece L yi icermektedir Boyut analizi bazen bir problemdeki bazi buyukluklerin alakasizligi ile ilgili veya ek degiskenler ekleme ile ilgili guclu ifadeleri aciga vurur Problemi dogru sekilde tanimlamak icin yeterli degisken sectiysek bu argumandan yola cikarak yay uzerindeki kutlenin periyodunun g den bagimsiz oldugu sonucuna varabiliriz Dunya da ve Ay da sonuc aynidir Problemimiz icin kuvvetlerin carpiminin varligini gosteren denklem esdeger bir yolla soyle yazilabilir T km k displaystyle T kappa sqrt m k bir boyutsuz sabit k displaystyle kappa icin Analizimizin durumun fiziksel tanimina ait olduguna emin oldugumuz bir degiskeni reddetmesi ile karsilastigimizda burada g reddedilen degiskenin durumla alakali oldugunu ve bizim durumla alakali baska degiskenleri reddedilen degiskenle beraber bir kombinasyonla boyutsuz bir buyukluk olusturabilecek sildigimiz ihtimalini dusunebiliriz Ancak burada durum o sekilde degildir Sadece kuvetlerin bir boyutsuz carpimini iceren problemlerde boyut analizi ile sonuca ulastigimizda burada oldugu gibi bilinmeyen fonksiyon yoktur ve cozum tamam dir denir Daha karmasik bir ornek l L displaystyle L uzunlugunda ve A L displaystyle L genligiyle titreyen bir teli goz onune alalim Telin lineer yogunlugu r dur M L displaystyle M L ve s ML T2 displaystyle ML T 2 gerilimine maruzdur ve bizde tel uzerindeki enerji E yi bulmak istiyoruz Simdi kolayca secilen degiskenlerin kuvvetlerinin carpimlari olan iki boyutsuz carpim elde edebiliriz p1 E As displaystyle pi 1 E As ve p2 ℓ A displaystyle pi 2 ell A Belki sasirtici bir sekilde yukarida verilen g ile ilgili basit ornekte lineer yogunluk soz konusu degildir Bulunan bu iki grup asagidaki denkleme donusturulebilir F E As ℓ A 0 displaystyle F E As ell A 0 burada F bilinmeyen bir fonksiyondur veya esit sekilde E Asf ℓ A displaystyle E Asf ell A burada f bilinmeyen baska bir fonksiyondur Burada bilinmeyen fonksiyon cozumumuzun tamamlanmadigi anlamina gelir fakat boyut analizi bize acik olmayan bazi seylerde vermisti Enerji gerilmenin ilk kuvvetiyle orantilidir Daha ileri analitik analiz haricinde bilinmeyen f fonksiyonunu bulmak icin deney de yapabiliriz Fakat deney yapmak eger boyut analizi mumkun degilse daha kolaydir Enerjinin gerilmeyle orantili oldugunu kanitlamak icin hicbir sey yapamazdik Veya belki enerjinin ℓ displaystyle ell e orantili oldugunu tahmin edebilirdik ve su sonuca varabilirdik E ℓs displaystyle E ell s Boyut analizinin deneylere yardimci olma ve hipotez yaratma gucu kanitlidir Yukaridakilere benzemeyen daha kompleks icerdigi degiskenlerin belirsiz oldugu ve temel denklemlerinin umutsuzca karmasik oldugu durumlara uygulandiginda boyut analizinin gucu gercekten belirginlesir Ornegin bir nehir yatagindaki kucuk bir cakil tasini dusunelim Eger nehir yeterince hizli akiyorsa cakiltasi yukselir ve su icinde yuzer Peki kritik hiz nedir Tahmin edilen degiskenleri cozmek daha oncekiler kadar kolay degildir Fakat boyut analizi bunun gibi problemleri anlamakta yardimci olabilir ve temel denklemlerin zr anlasildigi karmasik problemlerde uygulanacak ilk elemandir Huntley toplamiHuntley Huntley 1967 boyut kavramimizi zaman zaman rafine etmemizin verimli olacagini iddia etmistir Iki olasi rafinasyon sunlardir Bir vektorun bilesenlerinin buyukluklerinin boyutsal olarak farkli oldugu dusunulmelidir Ornegin For example farklilastirilmamis bir uzunluk birimi L dense Lx displaystyle L x gibi x yonun deki uzunlugu gosteren bir boyutu kullanabiliriz diger yonlerde de bu gecerlidir Bu gereklilik temel olarak fiziksel olarak anlamli bir denklemin her bir bileseninin skaler vektor veya tensor boyutsal olarak uyumlu olmasi gerekliligine dayanir Bir buyukluk olcusu olarak kutle bir atalet olcusu olan kutleden boyutsal olarak farkli dusunulmelidir Ilk rafinasyonun kullanisliliginin bir ornegi olarak dikey Vy displaystyle V y ve yatay Vx displaystyle V x hiziyla firlatilan bir topun topun yatay bir yuzeyden ateslendigini dusunelim ucus mesafesini hesap etmek istedigimizi varsayalim Yonlu uzunluklari kullanmadigimizi dusunursek ilgilendigimiz buyuklukler Vx displaystyle V x Vy displaystyle V y dir ve ikisinin de boyutu L T displaystyle L T dir R topun gittigi mesafe boyutu L ve g asagiya dogru yercekimi ivmesidir boyutu L T2 displaystyle L T 2 dir Bu dort buyuklukle R menzille ilgili asagidaki denkleme ulasabiliriz R VxaVybgc displaystyle R propto V x a V y b g c veya boyutsal olarak L L T a b L T2 c displaystyle L L T a b L T 2 c buradan bir katsayiyi tanimsiz birakan a b c 1 displaystyle a b c 1 ve a b 2c 0 displaystyle a b 2c 0 yi cikarabiliriz Bu beklenmelidir cunku iki temel buyukluk L ve T miz var ve bir denklemde dort degiskenimiz var Bununla birlikte eger yonlu uzunluk boyutlarini kullanirsak o zaman Vx displaystyle V x in boyutu Lx T displaystyle L x T Vy displaystyle V y nin boyutu Ly T displaystyle L y T R nin boyutu Lx displaystyle L x ve gnin boyutu da Ly T2 displaystyle L y T 2 olur Boyutsal denklem su hale gelir Lx Lx T a Ly T b Ly T2 c displaystyle L x L x T a L y T b L y T 2 c ve su sonuca variriz a 1 displaystyle a 1 b 1 displaystyle b 1 ve c 1 displaystyle c 1 Yonlu boyutlar kullanilarak elde edilen cikarim gucu acikca gorulmektedir Benzer sekilde ataletsel kutle ile maddesel kutleyi birbirinden ayirmak ornegin akiskanlar mekanigi ve termodinamikte zaman zaman kullanisli bulunabilir Ornegin Poiseuille Yasasi nin turetilmesini dusunelim Silindirik bir boru icinde viskoz bir akiskanin kutle akis oranini bulmak istiyoruz Eger ataletsel ve maddesel kutleyi birbirinden ayirmazsak ilgili su degiskenleri secebiliriz m displaystyle dot m M T displaystyle M T boyutlu kutle akis orani px displaystyle p x ML2 T2 displaystyle ML 2 T 2 boyutlu boru boyunca basinc gradyani r displaystyle rho M L3 displaystyle M L 3 boyutlu yogunluk h displaystyle eta M LT displaystyle M LT boyutlu dinamik akiskan viskozitesi r displaystyle r L displaystyle L boyutlu boru yaricapi Uc temel degisken vardir bu yuzden yukaridaki bes esitlik iki boyutsuz degiskene uyum saglar p1 m hr displaystyle pi 1 dot m eta r ve p2 pxrr5 m 2 displaystyle pi 2 p x rho r 5 dot m 2 ve boyut denklemini soyle ifade edebiliriz C p1p2a m hr pxrr5m 2 a displaystyle C pi 1 pi 2 a left frac dot m eta r right left frac p x rho r 5 dot m 2 right a burada C ve a belirsiz sabitlerdir Eger ataletsel kutle boyutu Mi displaystyle M i ve maddesel kutle boyutu Ms displaystyle M s arasindaki farki dusunursek kutle akis orani ve yogunluk maddesel kutleyi kutle parametresi olarak kullanirve burada basinc gradyani ve viskozite katsayisi ataletsel kutleyi kullanir Simdi dort temel parametremiz var ve bir tane de boyutsuz sabitimiz var boylece boyutsal denklemi soyle yazabiliriz C pxrr4hm displaystyle C frac p x rho r 4 eta dot m burada C belirsiz sabittir boyut analizi disindaki metotlarla p 8 displaystyle pi 8 olarak bulunur Bu denklem Poiseuille Yasasi kullanilarak kutle akis orani icin cozulebilir Engelleri ve Gelistirilmesi Yonelimsel cozumleme Huntley toplaminin bazi ciddi engelleri vardir Ne capraz carpim iceren vektor denklemleri ile ugrasir ve ne de acilari fiziksel degiskenler olarak iyi sekilde kullanir Ayrica genellikle ilgilenilen problemlerde L yi Lx displaystyle L x Ly displaystyle L y Lz displaystyle L z olarak gostermek de oldukca zordur Huntley fiziksel problemlerde simetri yi iceren bir proseduru hatirlatmaktadir Bu ise genellikle guvenilir sekilde uygulamak icin cok zordur simetri kavramini iceren problemin hangi parcasinin cagrilacagi acik degildir Bu kuvvetlerin uzerine etkidigi fiziksel govdenin simetrisi midir veya kuvvetlerin uygulandigi noktalarin cizgilerin veya alanlarin simetrisi midir Peki ya farkli simetrilerde birden fazla govde isin icindeyse Silindirik tupe eklenmis kuresel bir balonu dusunelim burada havanin akis oranini basinc degisiminin bir fonksiyonu olarak iki parcada isteriz Bagli parcalarda tasinan havanin viskozitesinin genisletilmis Huntley boyutlari nelerdir Bu iki parcanin basincinin genisletilmis boyutlari nelerdir Bu zorluklar Huntley toplaminin gercek problemlere uygulamasindaki kisitlamalardan sorumludur Acilar geleneksel olarak boyutsuz degiskenler olarak dusunulmektedirler ve bu yuzden boyut analizinde acilarin fiziksel degisken olarak kullanimi daha az anlamli sonuclar verir Ornegin yukaridaki top ornegini dusunelim Dusunun ki x ve y ilk hiz bilesenleri yerine hizin buyuklugu v ve firlatilis acisi 8 displaystyle theta yi secelim Aci geleneksel olarak boyutsuz olarak dusunulur ve bir vektorun buyuklugu yonle ilgili bir bilgi tasimamaktadir bu yuzden g v R ve 8 degiskenlerindenhicbir boyutsuz degisken olusturulamaz Geleneksel analiz dogru sekilde g ve v nin kuvvetlerini verir fakat boyutsuz aci 8 ile ilgili hicbir bilgi vermez Siano Siano 1985 I 1985 II Huntley in yonlu boyutlarinin vektorlerin yonlerini ve yonelimsiz sembol 10 displaystyle 1 0 i ifade etmek icin yonelimsel semboller 1x 1y 1z displaystyle 1 x 1 y 1 z i onermistir Boylece Huntley in Lx displaystyle L x si L ile L1x displaystyle L 1 x haline gelir uzunluk boyutunu belirtir ve 1x displaystyle 1 x de yonelimi belirtir Siano daha sonra yonelimsel sembollerin kendi cebirleri oldugunu gostermistir 1i 1 1i displaystyle 1 i 1 1 i gerekliligi ile birlikte asagida yonelim sembollerinin carpim tablosu gosterilmistir 101x1y1z10101x1y1z1x1x101z1y1y1y1z101x1z1z1y1x10 displaystyle begin matrix amp mathbf 1 0 amp mathbf 1 x amp mathbf 1 y amp mathbf 1 z mathbf 1 0 amp 1 0 amp 1 x amp 1 y amp 1 z mathbf 1 x amp 1 x amp 1 0 amp 1 z amp 1 y mathbf 1 y amp 1 y amp 1 z amp 1 0 amp 1 x mathbf 1 z amp 1 z amp 1 y amp 1 x amp 1 0 end matrix Yonelimsel sembollerin matematiksel grup olusturduguna dikkat edin Bu sistemde skalerler problemin simetrisi nden bagimsiz olarak daima ayni yonelimi tanimlayici eleman olarak bulundurur Vektor olan fiziksel buyuklukler ise su yonelimlere sahiptirler x yonlu bir kuvvetin veya hizin yonelimi 1x displaystyle 1 x dir Acilar icin z duzleminde bir 8 acisi dusunun z duzleminde acilarindan biri 8 olan bir dik ucgen cizin Dik ucgenin acimizin yanindaki kenarinin yonelimi 1x displaystyle 1 x olur ve diger kenarinda yonelimi 1y displaystyle 1 y olur Sonra tan 8 ly lx 8 oldugundan xy duzlemindeki bir acinin 1y displaystyle 1 y 1x displaystyle 1 x 1z displaystyle 1 z yonelimine sahip oldugu sonucuna variriz ki bu da oldukca mantiklidir Benzer sekilde sin 8 nin yonelimi 1z displaystyle 1 z ve cos 8 nin yonelimi de 10 displaystyle 1 0 dir Bunlar farklidir bu yuzden a ve b skalerken a sin 8 b cos 8 seklindeki fiziksel esitlklerin cozumu olmadigi sonucuna varan biri dogru bir sonuc bulmus olur Fiziksel buyukluklerin yonelimsel sembollerinin gorevleri ve fiziksel denklemlerin yonelimsel olarak homojen olma gereklilikleri gercekte boyut analizine fiziksel problemlerin kabul edilebilir cozumleri hakkinda cok az bilgi turetme acisindan benzerdir Bu sebepten boyutsal denklemi kurdugumuzda ancak yapabildigimiz kadarini cozeriz Eger bir fiziksel degiskenin en dusuk kuvveti kesirli ise cozumun her iki tarafi da tgm kuvvetlerin integrali alinmis gibi bir kuvvete yukselir Bu da denklemi normal form a getirir Daha sonra yonelimsel denklem yonelimsel sembollerin bilinmeyen kuvvetlerine daha kisitlayici sartlar koymak icin cozulur ve boyut analizinin tek basina verdigi sonuctan daha tam bir sonuca ulasilir Siklikla eklenen bilgi belli bir degiskenin kuvvetlerinden birinin tek mi cift mi oldugudur Ornegin firlatma probleminde yonelimsel sembolleri kullanirsak 8 x y duzleminde olacaktir ve boyutu 1z displaystyle 1 z olacaktir ve menzil R soyle olacaktir R gavb8c displaystyle R g a v b theta c bunun anlami sudur L1x L1yT2 a LT b1zc displaystyle L 1 x sim left frac L 1 y T 2 right a left frac L T right b 1 z c Boyutsal homojenlik simdi dogru sekilde a 1 ve b 2 yi saglar ve yonelimsel homojenlik c nin bir tek tam sayi olmasini gerektirir Aslinda 8 nin gereksinilen fonksiyonu sin 8 cos 8 displaystyle sin theta cos theta olacaktir ve bu da 8 displaystyle theta nin tek kuvvetlerinin bir serisidir Yukaridaki carpim tablosunu kullandigimizda sin 8 displaystyle sin theta ve cos 8 displaystyle cos theta nin Taylor serileri yonelimsel olarak homojendir cos 8 sin 8 displaystyle cos theta sin theta ve exp 8 displaystyle exp theta nin Taylor serileri homojen degildir ve fiziksel olmadiklari varsayilir Yonelimsel semboller icin kullanilan carpim kuralinin iki vektorun capraz carpimi kuraliyla ayni oldugu aciktir Iki ozdes vektorun capraz carpimlari sifirdir nitekim ozdes iki yonelimsel sembolun carpimi da ozdes elemandir Felsefi temelSonuc olarak boyut analizi ve fiziksel esitliklerin boyutsal olarak homojen olmasi gerekliligi fizik kanunlarinin fiziksel buyuklukleri olcmekde kullanilan birimlerden bagimsiz oldugu fikrini yansitir Yani ornegin eger SI sistemi Ingiliz birim sistemi cgs sistemi veya herhangi baska bir uygun birim sistemi kullanildiginda F ma denklemi dogrudur Yonelimsel analiz ve fiziksel denklemlerin yonelimsel olarak homojen olmasi gerekliligi de fizik denkleminin kullanilan koordinat sisteminden bagimsiz olmasini gerektirdigi fikrini yansitir Boyutsuz sabitlerPoiseuille in kanunundaki C ve yukarida tartisilan yay problemi ile ilgili k displaystyle kappa gibi ulasilan sonuclardan elde edilen boyutsuz sabitler temelde yatan fizigin daha detayli analizinden elde edilir ve siklikla bazi diferansiyel denklemlerin integre edilmesiyle bulunur Boyut analizinin bu sabitlerle ilgili fazla soyleyebilecegi bir sey yoktur fakat basamak birligi buyuklugunu ogrenmekte kulanislidir Bu gozlem bize bazen ilgilendigimiz problemle ilgili cok zor hesaplamalari yapmakda izin verir ve boylece olcum yapacagimiz veya onemli olup olmadigina karar verecegimiz deneyleri daha verimli tasarlamamiza olanak saglar Buckingham p teoremiboyut analizinin temelini olusturan bir yontemdir Bu teorem n adet degisken iceren her anlamli fiziksel denklemin n m boyutsuz parametreli denklemle yeniden yazilabilecegini soyler burada m kullanilan temel boyutlarin sayisidir Dahasi ve daha onemlisi teorem bu boyutsuz degiskenleri verilen degiskenlerden hesaplamak icin bir yontem saglar KaynakcaBhaskar R 1990 Qualitative Physics Using Dimensional Analysis Artificial Intelligence Cilt 45 ss 73 111 Bhaskar R 1991 Qualitative Explanations of Red Giant Formation The Astrophysical Journal Cilt 372 ss 592 6 Boucher 1960 Dimensionless Numbers Chem Eng Progress Cilt 55 ss 55 64 1914 On Physically Similar Systems Illustrations of the Use of Dimensional Analysis Phys Rev Cilt 4 s 345 Klinkenberg A 1955 Dimensional systems and systems of units in physics with special reference to chemical engineering Part I The principles according to which dimensional systems and systems of units are constructed Chemical Engineering Science 4 3 ss 130 140 167 177 doi 10 1016 0009 2509 55 80004 8 Moody L F 1944 Friction Factors for Pipe Flow Trans Am Soc Mech Engrs 66 671 Murphy N F 1949 Dimensional Analysis Bull V P I 42 6 Perry J H 1944 Standard System of Nomenclature for Chemical Engineering Unit Operations Trans Am Inst Chem Engrs 40 251 Petty G W 2001 Automated computation and consistency checking of physical dimensions and units in scientific programs Software Practice and Experience Cilt 31 ss 1067 1076 Lord Rayleigh 1915 The Principle of Similitude Nature Cilt 95 ss 66 68 Siano Donald 1985 Orientational Analysis A Supplement to Dimensional Analysis I J Franklin Institute 320 s 267 Siano Donald 1985 Orientational Analysis Tensor Analysis and The Group Properties of the SI Supplementary Units II J Franklin Institute 320 s 285 Silberberg I H 1953 Learning How to Use Dimensional Analysis Petrol Refiner 32 4 p 5 5 p 147 6 p 101 7 p 129 Van Driest E R Mart 1946 On Dimensional Analysis and the Presentation of Data in Fluid Flow Problems J App Mech 68 A 34 Dis baglantilarhttp en wikibooks org wiki Fluid Mechanics Ch4 8 Nisan 2009 tarihinde Wayback Machine sitesinde arsivlendi Unicalc Live web calculator doing units conversion by dimensional analysis 22 Aralik 2008 tarihinde Wayback Machine sitesinde http www math ntnu no hanche notes buckingham buckingham a4 pdf 20 Eylul 2008 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans