Bir dalganın grup hızı, dalga şiddetinin genel şekli (dalga modülasyonu veya sarımı) ile boşlukta yayılan hızıdır. Örneğin, bir taşın, durgun bir su birikintisinin ortasına atıldığında ne olabileceğini düşünelim. Taş suyun yüzeyine geldiği anda, o bölgede dairesel dalgalanmalar meydana gelir. Kısa bir süre içinde, hareketsiz bir merkezden yayılan bu dalgalar dairesel halkalara dönüşür. Giderek genişleyen bu dairesel halkalar, farklı hızlarda yayılan ve farklı dalga boylarına sahip daha küçük dalgaları kendi içerisinde birbirinden ayırabilen bir dalga grubudur. Uzun dalgalar, tüm gruba kıyasla daha hızlı yol alabilirken; sona doğru yaklaştıkça kaybolurlar. Kısa dalgalar ise daha yavaş yol alırlar ve bir önceki dalga sınırına ulaştıklarında yok olurlar.


Tanım ve açıklama
Tanım

Grup hızı, yani Vg aşağıdaki denklem ile tanımlanabilir;
Bu denklemde ω dalgaların açısal tekrar sıklığını (genellikle saniye başına düşen radyan sayısı ile ifade edilir) ve k açısal dalga sayısını (genellikle metre başına düşen radyan sayısı ile ifade edilir) gösterir. ω(k) fonksiyonu, “dağılım ilişkisi” olarak bilinir.
- Eğer ω doğrudan k ile orantılıysa, o zaman grup hızı, tam olarak faz hızına eşit olur. Şekli ne olursa olsun, bir dalga, bu hızda, dağılmadan yol alacaktır.
- Eğer ω, k’ nın çizgisel fonksiyonu ama doğru orantılı değilse (ω=ak+b), bu durumda grup hızı ile faz hızı birbirinden farklı olacaktır. Dalga paketi sarmalı, grup hızında ilerlerken, her bir dalga tekrar sıklığı -bireysel olarak- faz hızında hareket eder.
- Eğer ω, k’ nın çizgisel fonksiyonu değil ise, dalga paketi hareket ettikçe bozulacaktır. Bu bozulma doğrudan grup hızını etkiler. Bir dalga paketi, farklı tekrar sıklıklar içerdiğinden, grup hızı - ∂ω/∂k- farklı değerler alabilir çünkü ω, k’ nın çizgisel bir fonksiyonu değildir. Sonuç olarak sarmal tek bir hızda değil, farklı hızlar aralığında hareket eder ve bu sarmalın bozulmasına neden olur.
Türev
Grup hızı formülünün başka bir türevi de aşağıdaki gibidir; Dalga paketinin, x konumundaki ve t süresindeki fonksiyonunu t: α(x,t) olarak alalım, t=0 aldığımızda, A(k) onun Fourier dönüşümü olsun;
Çakışma prensibiyle, herhangi bir zamanda dalga paketindeki t aşağıdaki gibi olacaktır;
(Burada ω, dolaylı olarak knın bir fonksiyonudur.)
Burada, A(k) sadece merkez dalga boyunda k 0 sıfırdan farklı bir değerde olabilsin diye dalga paketinin neredeyse monokromatik olduğunu varsayıyoruz. Daha sonra doğrusallaştırma aşağıdaki gibi olacaktır;
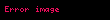

Örneğin bir dalga paketi; 
Dağınımda yüksek mertebe terimler

Bir önceki türevin bir kısmı varsayımdır.
Eğer dalga grubu geniş bir yayılma tekrarsıklığına sahip ise ya da yayılma hızı 

Fiziksel tanım
Grup hızı genellikle enerjinin veya bilginin bir dalga boyunca taşındığı hız olarak düşünülür. Birçok durumda bu doğrudur ve grup hızı aynı zamanda dalga şekli sinyali olarak da nitelendirilebilir. Ancak, eğer dalga emici bir ortamda hareket ediyorsa, bu bilgi her zaman doğru olmaz. 1980lerden beri yapılan birçok araştırma ve deney gösterdi ki özel olarak hazırlanmış materyallerle gönderilen lazer ışığının grup hızı, hava boşluğunda ışık hızını geçebilir. Ancak bu durumda, ışık hızından daha hızlı bir iletişim mümkün değildir çünkü sinyal hızı ışık hızından her şekilde daha yavaş kalır. Akımı durdurarak ya da negatif grup hızı oluşturarak, grup hızını sıfıra düşürmek de mümkündür. Ancak tüm durumlarda, fotonlar ortamda beklenilen ışık hızında yayılmaya devam eder.
Tarihi
Grup hızının, dalgaların faz hızından farklı olduğu fikri ilk olarak 1839 yılında W.R. Hamilton tarafından ortaya atılmıştır
Diğer açıklamalar
Işık için, kırılma indisi n,boşluk dalga boyu λ0 ve orta dalga λ aşağıdaki formül ile ilişkilidir.
Vp = ω/k faz hızı. Bu nedenle, grup hızı takip eden formül ile hesaplanabilir.
Üç Boyutta
Işık, ses ve madde dalgaları gibi üç boyutlu hareket eden dalgalar için, grup hızı ve faz hızı formülleri basit bir şekilde genelleşmiştir;
- Tek boyut:
- Üç boyut:

Kaynakça
İngilizce Vikipedi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bir dalganin grup hizi dalga siddetinin genel sekli dalga modulasyonu veya sarimi ile boslukta yayilan hizidir Ornegin bir tasin durgun bir su birikintisinin ortasina atildiginda ne olabilecegini dusunelim Tas suyun yuzeyine geldigi anda o bolgede dairesel dalgalanmalar meydana gelir Kisa bir sure icinde hareketsiz bir merkezden yayilan bu dalgalar dairesel halkalara donusur Giderek genisleyen bu dairesel halkalar farkli hizlarda yayilan ve farkli dalga boylarina sahip daha kucuk dalgalari kendi icerisinde birbirinden ayirabilen bir dalga grubudur Uzun dalgalar tum gruba kiyasla daha hizli yol alabilirken sona dogru yaklastikca kaybolurlar Kisa dalgalar ise daha yavas yol alirlar ve bir onceki dalga sinirina ulastiklarinda yok olurlar Bu grafik faz hizi ve grup hizi farkli yonlere giden bir dalgayi gosterir Tanim ve aciklamaTanim Duz Cizgi Dalga pakti Kesikli Cizgi Dalga paketinin sarimi Sarim grup hizinda hareket eder Grup hizi yani Vg asagidaki denklem ile tanimlanabilir vg w k displaystyle v g equiv frac partial omega partial k Bu denklemde w dalgalarin acisal tekrar sikligini genellikle saniye basina dusen radyan sayisi ile ifade edilir ve k acisal dalga sayisini genellikle metre basina dusen radyan sayisi ile ifade edilir gosterir w k fonksiyonu dagilim iliskisi olarak bilinir Eger w dogrudan k ile orantiliysa o zaman grup hizi tam olarak faz hizina esit olur Sekli ne olursa olsun bir dalga bu hizda dagilmadan yol alacaktir Eger w k nin cizgisel fonksiyonu ama dogru orantili degilse w ak b bu durumda grup hizi ile faz hizi birbirinden farkli olacaktir Dalga paketi sarmali grup hizinda ilerlerken her bir dalga tekrar sikligi bireysel olarak faz hizinda hareket eder Eger w k nin cizgisel fonksiyonu degil ise dalga paketi hareket ettikce bozulacaktir Bu bozulma dogrudan grup hizini etkiler Bir dalga paketi farkli tekrar sikliklar icerdiginden grup hizi w k farkli degerler alabilir cunku w k nin cizgisel bir fonksiyonu degildir Sonuc olarak sarmal tek bir hizda degil farkli hizlar araliginda hareket eder ve bu sarmalin bozulmasina neden olur Turev Grup hizi formulunun baska bir turevi de asagidaki gibidir Dalga paketinin x konumundaki ve t suresindeki fonksiyonunu t a x t olarak alalim t 0 aldigimizda A k onun Fourier donusumu olsun a x 0 dkA k eikx displaystyle alpha x 0 int infty infty dk A k e ikx Cakisma prensibiyle herhangi bir zamanda dalga paketindeki t asagidaki gibi olacaktir a x t dkA k ei kx wt displaystyle alpha x t int infty infty dk A k e i kx omega t Burada w dolayli olarak knin bir fonksiyonudur Burada A k sadece merkez dalga boyunda k0 sifirdan farkli bir degerde olabilsin diye dalga paketinin neredeyse monokromatik oldugunu varsayiyoruz Daha sonra dogrusallastirma asagidaki gibi olacaktir w k w0 k k0 w0 displaystyle omega k approx omega 0 k k 0 omega 0 w0 w k0 displaystyle omega 0 omega k 0 ve w0 w k k k k0 displaystyle omega 0 frac partial omega k partial k k k 0 Daha sonra bu esitlemelerden asagidaki sonuca ulasiriz a x t eit w0 k0 w0 dkA k eik x w0 t displaystyle alpha x t e it omega 0 k 0 omega 0 int infty infty dk A k e ik x omega 0 t a x t a x w0 t 0 displaystyle alpha x t alpha x omega 0 t 0 Ornegin bir dalga paketi w0 dw dk k k0 displaystyle omega 0 d omega dk k k 0 hizinda hareket etmektedir Bu grup hizi formulunu aciklar Daginimda yuksek mertebe terimler Bir onceki turevin bir kismi varsayimdir w k w0 k k0 w0 displaystyle omega k approx omega 0 k k 0 omega 0 Eger dalga grubu genis bir yayilma tekrarsikligina sahip ise ya da yayilma hizi w k displaystyle omega k keskin varyasyonlara sahip ise ornegin direnc gibi ya da eger dalga grubu cok uzun mesafelere hareket ediyorsa bu varsayim gecerli degildir Sonuc olarak dalga grubunun dalgalari sadece hareket etmiyor ayni zamanda sapiyor Genis anlamda dalga grubunun farkli tekrarsiklik bilesenleri farkli hizlarda hareket eder Dalga grubunun onune dogru hareket eden bilesenler daha hizli dalga boyunun arkasina dogru hareket eden bilesenler daha yavastir En sonunda dalga grubu uzamis olur Taylor serisindeki bir sonraki mertebe w k displaystyle omega k tureviyle ilgilidir grup hizi yayilimi olarak adlandirilir Ve bu kisa darbeli lazerlerde yuksek enerji tasariminda ve fiberoptik sinyallerde ki en onemli etkidir Fiziksel tanim Grup hizi genellikle enerjinin veya bilginin bir dalga boyunca tasindigi hiz olarak dusunulur Bircok durumda bu dogrudur ve grup hizi ayni zamanda dalga sekli sinyali olarak da nitelendirilebilir Ancak eger dalga emici bir ortamda hareket ediyorsa bu bilgi her zaman dogru olmaz 1980lerden beri yapilan bircok arastirma ve deney gosterdi ki ozel olarak hazirlanmis materyallerle gonderilen lazer isiginin grup hizi hava boslugunda isik hizini gecebilir Ancak bu durumda isik hizindan daha hizli bir iletisim mumkun degildir cunku sinyal hizi isik hizindan her sekilde daha yavas kalir Akimi durdurarak ya da negatif grup hizi olusturarak grup hizini sifira dusurmek de mumkundur Ancak tum durumlarda fotonlar ortamda beklenilen isik hizinda yayilmaya devam eder Tarihi Grup hizinin dalgalarin faz hizindan farkli oldugu fikri ilk olarak 1839 yilinda W R Hamilton tarafindan ortaya atilmistir Diger aciklamalar Isik icin kirilma indisi n bosluk dalga boyu l0 ve orta dalga l asagidaki formul ile iliskilidir l0 2pcw l 2pk 2pvpw n cvp l0l displaystyle lambda 0 frac 2 pi c omega lambda frac 2 pi k frac 2 pi v p omega n frac c v p frac lambda 0 lambda Vp w k faz hizi Bu nedenle grup hizi takip eden formul ile hesaplanabilir vg cn w n w cn l0 n l0 vp 1 ln n l vp l vp l vp k vp k displaystyle v g frac c n omega frac partial n partial omega frac c n lambda 0 frac partial n partial lambda 0 v p left 1 frac lambda n frac partial n partial lambda right v p lambda frac partial v p partial lambda v p k frac partial v p partial k Uc BoyuttaIsik ses ve madde dalgalari gibi uc boyutlu hareket eden dalgalar icin grup hizi ve faz hizi formulleri basit bir sekilde genellesmistir Tek boyut vp w k vg w k displaystyle v p omega k quad v g frac partial omega partial k Uc boyut vp k w k vg kw displaystyle mathbf v p hat mathbf k frac omega mathbf k quad mathbf v g vec nabla mathbf k omega kw displaystyle vec nabla mathbf k omega acisal frekansin dusumu k displaystyle mathbf k dalga vektorunun fonksiyonu ve k displaystyle hat mathbf k k nin birim vektorudur Eger dalgalar kristal gibi esyonsuz bir ortamda yayiliyorsa o zaman grup hizi vektoru ile faz hizi vektoru farkli yonleri gosterebilir KaynakcaIngilizce Vikipedi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans