Matematiğin bir alt dalı olan stokastik süreçlerde Doléans-Dade üsteli, Doléans üsteli ya da stokastik üstel, matematiksel analizin üstel fonksiyonuna stokastik süreçlerde karşılık gelen bir kavramdır. Bu kavram adını Fransız asıllı Amerikalı matematikçi Catherine Doléans-Dade'den almaktadır.
Stokastik üstel kavramı açık çözümlerini yazarken karşımıza çıkar. Girsanov teoreminin formülasyonunda da önemli bir yer tutar. Bu bağlamda en temel sorulardan birisi stokastik üstelin ne zaman martingal olacağıdır. Matematiksel finans modellerinin çoğu stokastik üstel olan süreçleri barındırmaktadır. Bunlardan önemli olan bir tanesi de Black-Scholes modelindeki .
Giriş
Üstel fonksiyon 
ve
.
Daha genel durum ise zincir kuralı kullanılarak halledilebilir; diğer deyişle, 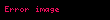
ve
şartlarıyla biricik olarak belirlenir.
Bu mekanizmayı kolaylıkla taşımak mümkün değildir. Buradaki ilk zorluk, zincir kuralının yerini alan ve süreçlerin (varyasyon) göz önüne almak zorunda olan . Örneğin, 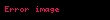

elde edilir. Bu diferansiyel denklemde ek olarak gelen 



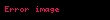
Tanım









olarak gösterilir.
Genel formül ve özel durumlar
sürekli ve
de
'in olursa, o zaman
- olur. Gerçekten de,
'nun yarı martingal, sürekli ve kati bir şekilde pozitif olduğunu kabul edelim. O zaman,
üstüne uygularsak
- elde ederiz. Here iki tarafın üstel fonksiyonunu alırsak ve
olduğunu göz önünde tutarsak,
Brown hareketi ise, o zaman stokastik üstel olur.
- Genel durumda ise
'in sıçrama yaptığı noktalar göz önüne alınmalıdır. Yani, eğer
sadece yarı martingalse ve sıçrama süreci
olarak alınırsa,
- olur.
- Üstel fonksiyonun fonksiyonel eşitliği olan
ifadesine karşılık stokastik üstelde
yarı martingal olmak üzere
- ifadesi vardır. Bu formüle Fransız matematikçi 'a atfen Yor formülü adı verilir.
Özellikler
- Stokastik üstel sürekli olarak sıfıra gidemez, sadece sıfıra sıçrayabilir. Bu nedenle, sürekli bir yarı martingalin stokastik üstel değeri her zaman kesinlikle pozitiftir.
- Stokastik üstel
sıfıra bir kere sıçradığında burada yani sıfır değerinde absorbe edilir. Sıfıra ilk sıçradığı zaman ise tam olarak
olduğu zamandır.
'in sadece
zamanındaki değerine bağlı olan doğal üstel fonksiyon
'nin davranışının aksine,
sadece
'ye bağlı olmakla kalmaz. Dahası,
'in
zaman aralığındaki bütün geçmiş değerlerine bağlıdır. Bu yüzden,
yazılmalıdır; yani,
doğru bir notasyon değildir.
- Bir yerel martingalin stokastik üsteli yine bir yerel martingaldir.
- Yukarıdaki tüm formüller ve özellikler, karmaşık değerli bir
'in stokastik üsteline de uygulanır. Bu uygulamanın, konform martingaller teorisinde ve karakteristik fonksiyonların hesaplanmasında uygulamaları vardır.
Ayrıca bakınız
Kaynakça
- ^ Doléans-Dade, C. (1970). "Quelques applications de la formule de changement de variables pour les semimartingales". Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete (Fransızca). 16 (3). ss. 181-194. doi:10.1007/BF00534595. ISSN 0044-3719.
- ^ Yor, Marc (1976), "Sur les integrales stochastiques optionnelles et une suite remarquable de formules exponentielles", Séminaire de Probabilités X Université de Strasbourg, Lecture Notes in Mathematics, 511, Berlin, Heidelberg: Springer Berlin Heidelberg, ss. 481-500, doi:10.1007/bfb0101123, ISBN , 26 Ocak 2022 tarihinde kaynağından arşivlendi, erişim tarihi: 14 Aralık 2021
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan stokastik sureclerde Doleans Dade usteli Doleans usteli ya da stokastik ustel matematiksel analizin ustel fonksiyonuna stokastik sureclerde karsilik gelen bir kavramdir Bu kavram adini Fransiz asilli Amerikali matematikci Catherine Doleans Dade den almaktadir Stokastik ustel kavrami acik cozumlerini yazarken karsimiza cikar Girsanov teoreminin formulasyonunda da onemli bir yer tutar Bu baglamda en temel sorulardan birisi stokastik ustelin ne zaman martingal olacagidir Matematiksel finans modellerinin cogu stokastik ustel olan surecleri barindirmaktadir Bunlardan onemli olan bir tanesi de Black Scholes modelindeki GirisUstel fonksiyon u t et displaystyle u t mathrm e t diferansiyel denklemler baglaminda iki sartla biricik olarak belirlenir u t u t displaystyle u t u t ve u 0 1 displaystyle u 0 1 Daha genel durum ise zincir kurali kullanilarak halledilebilir diger deyisle u t ex t x 0 displaystyle u t mathrm e x t x 0 fonksiyonu u t u t x t displaystyle u t u t x t ve u 0 1 displaystyle u 0 1 sartlariyla biricik olarak belirlenir Bu mekanizmayi kolaylikla tasimak mumkun degildir Buradaki ilk zorluk zincir kuralinin yerini alan ve sureclerin varyasyon goz onune almak zorunda olan Ornegin Wt displaystyle W t standart Wiener sureciyse ve Ut u Wt eWt displaystyle U t u W t mathrm e W t alinirsa o zaman kullanilarak dUt eWtdWt 12eWtdt Ut dWt 12dt displaystyle mathrm d U t mathrm e W t mathrm d W t frac 1 2 mathrm e W t mathrm d t U t left mathrm d W t frac 1 2 mathrm d t right elde edilir Bu diferansiyel denklemde ek olarak gelen dt displaystyle dt teriminden kacinmak icin ustel fonksiyonun biraz degistirilmis bir baska deyisle duzeltilmis hali kullanilir Eger Ut eWt 12t displaystyle U t mathrm e W t frac 1 2 t alinirsa ve kullanilirsa dUt UtdWt displaystyle mathrm d U t U t mathrm d W t elde edilir Bunlara ek olarak Ut displaystyle U t sureci Wt displaystyle W t gibi bir martingal olur TanimX Xt t R displaystyle X X t t in mathbb R bir olsun Ut displaystyle U t U displaystyle U surecinin t displaystyle t noktasinda soldan limiti olmak uzere dUt Ut dXt U0 1 displaystyle dU t U t dX t quad quad U 0 1 biricik guclu cozumu olan U Ut t R displaystyle U U t t in mathbb R yari martingaline X displaystyle X surecinin Doleans Dade usteli Doleans usteli ya da stokastik usteli denir ve E X displaystyle mathcal E X ile gosterilir Yani E X t Ut displaystyle mathcal E X t U t Ayni cozum temsili ile Ut 1 0tUs dXs displaystyle U t 1 int 0 t U s mathrm d X s olarak gosterilir Genel formul ve ozel durumlarX Xt t R displaystyle X X t t in mathbb R surekli ve X X displaystyle X X de X displaystyle X in olursa o zamanE X t eXt X0 12 X X t displaystyle mathcal E X t mathrm e X t X 0 frac 1 2 X X t olur Gercekten de U displaystyle U nun yari martingal surekli ve kati bir sekilde pozitif oldugunu kabul edelim O zaman f U log U displaystyle f U log U ustune uygularsak log Ut log U0 0t1UsdUs 0t12Us2d U s Xt X0 12 X X t displaystyle begin aligned log U t log U 0 amp int 0 t frac 1 U s dU s int 0 t frac 1 2U s 2 d U s X t X 0 frac 1 2 X X t end aligned elde ederiz Here iki tarafin ustel fonksiyonunu alirsak ve U0 1 displaystyle U 0 1 oldugunu goz onunde tutarsak Ut eXt X0 12 X X t t 0 displaystyle U t e X t X 0 frac 1 2 X X t qquad t geq 0 X displaystyle X Brown hareketi ise o zaman stokastik ustel olur Genel durumda ise X displaystyle X in sicrama yaptigi noktalar goz onune alinmalidir Yani eger X displaystyle X sadece yari martingalse ve sicrama sureci DXs Xs Xs displaystyle Delta X s X s X s olarak alinirsa E X t eXt X0 12 X X t s t 1 DXs e DXs 12 DXs 2 displaystyle mathcal E X t mathrm e X t X 0 frac 1 2 X X t prod s leq t 1 Delta X s mathrm e Delta X s frac 1 2 Delta X s 2 olur Ustel fonksiyonun fonksiyonel esitligi olan ex y exey displaystyle e x y e x e y ifadesine karsilik stokastik ustelde X t Y t displaystyle X t Y t yari martingal olmak uzereE X tE Y t E X Y X Y t displaystyle mathcal E X t mathcal E Y t mathcal E X Y X Y t ifadesi vardir Bu formule Fransiz matematikci a atfen Yor formulu adi verilir OzelliklerStokastik ustel surekli olarak sifira gidemez sadece sifira sicrayabilir Bu nedenle surekli bir yari martingalin stokastik ustel degeri her zaman kesinlikle pozitiftir Stokastik ustel E X displaystyle mathcal E X sifira bir kere sicradiginda burada yani sifir degerinde absorbe edilir Sifira ilk sicradigi zaman ise tam olarak DX 1 displaystyle Delta X 1 oldugu zamandir X displaystyle X in sadece t displaystyle t zamanindaki degerine bagli olan dogal ustel fonksiyon eXt displaystyle e X t nin davranisinin aksine E X t displaystyle mathcal E X t sadece Xt displaystyle X t ye bagli olmakla kalmaz Dahasi X displaystyle X in 0 t displaystyle 0 t zaman araligindaki butun gecmis degerlerine baglidir Bu yuzden E X t displaystyle mathcal E X t yazilmalidir yani E Xt displaystyle mathcal E X t dogru bir notasyon degildir Bir yerel martingalin stokastik usteli yine bir yerel martingaldir Yukaridaki tum formuller ve ozellikler karmasik degerli bir X displaystyle X in stokastik usteline de uygulanir Bu uygulamanin konform martingaller teorisinde ve karakteristik fonksiyonlarin hesaplanmasinda uygulamalari vardir Ayrica bakinizGirsanov teoremiKaynakca Doleans Dade C 1970 Quelques applications de la formule de changement de variables pour les semimartingales Zeitschrift fur Wahrscheinlichkeitstheorie und Verwandte Gebiete Fransizca 16 3 ss 181 194 doi 10 1007 BF00534595 ISSN 0044 3719 Yor Marc 1976 Sur les integrales stochastiques optionnelles et une suite remarquable de formules exponentielles Seminaire de Probabilites X Universite de Strasbourg Lecture Notes in Mathematics 511 Berlin Heidelberg Springer Berlin Heidelberg ss 481 500 doi 10 1007 bfb0101123 ISBN 978 3 540 07681 0 26 Ocak 2022 tarihinde kaynagindan arsivlendi erisim tarihi 14 Aralik 2021
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans





















