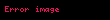Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının için kullanılır.

Bu gösterim ilk olarak Alman sayılar kuramcısı tarafından 1892 yılında yazdığı Analytische Zahlentheorie kitabında kullanılmıştır. Gösterim bir başka Alman matematikçi olan Edmund Landau tarafından yaygın kullanıma sokulmuştur, bundan ötürü bazen olarak da anılır. Büyük O, İngiliz dilindeki "order of" yani bir şeyin derecesi anlamına gelen söz öbeğini hatırlatmak amacı ile kullanılıyordu ve ilk olarak büyük harfi idi; günümüzde büyük O kullanılmakta ve 0 sayısı hiç kullanılmamaktadır.
Kullanım alanları
Bu gösterimin biçimsel olarak yakın ama temelde farklı iki kullanımı vardır: sonsuz ve asimptotikler. Bu ayrım sadece uygulamadadır ancak "büyük O"nun biçimsel tanımı her iki durumda aynı olup işlev argümanının limitleri değişmektedir.
Sonsuz asimptotikler
Büyük O gösterimi faydalıdır. Söz gelimi n boyundaki bir problemi çözmek için gereken zaman (adım sayısı) T(n) = 4n² - 2n + 2 olarak bulunabilir.
n büyüdükçe n² terimi o kadar hızlı büyüyecektir ki diğer terimlerin büyüme hızı buna kıyasla ihmal edilebilecek kadar düşük kalacaktır; örneğin n = 500 için 4n² terimi 2n teriminin 1000 katı büyüklüğünde olacaktır ve dolayısıyla bu ikinci terimin değeri tüm ifadenin değerini belirlemede çoğu amaç bakımından ihmal edilebilir bir etkiye sahip olacaktır.
Buna ek olarak, aynı ifadeyi n³ veya 2n terimleri içeren bir ifade ile kıyaslayacak olursak katsayılar da anlamlarını yitirecektir. T(n) = 1.000.000n² ve U(n) = n³ olsa bile ikinci ifade, n 1.000.000'u geçtikçe birinci ifadeye kıyasla daima daha büyük olacaktır (T(1.000.000) = 1.000.000³ = U(1.000.000)).
O halde Büyük O gösterimi işin özünü sade biçimde sunmaktadır: şu şekilde yazabilir
ve algoritmanın n2 dereceden zaman karmaşıklığına sahip olduğunu söyleyebiliriz.
Sonsuz küçük asimptotikler
Büyük O aynı zamanda bir matematiksel işlev için geliştirilen yaklaşık işlevin hata terimini tarif etmek için de kullanılabilir. Örneğin, :
Biçimsel tanım
f(x) ve g(x) gerçel sayılar kümesinin bir alt kümesi üzerinde tanımlanmış iki işlev olsun. Bu durumda deriz ki
- f(x), O(g(x))dir; x
∞
yalnız ve yalnız
- öyle x0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; x > x0 için.
Aynı gösterim f işlevinin bir a gerçel sayısı civarındaki davranışını tarif etmek için de kullanılabilir: Deriz ki
- f(x) O(g(x))dir; x
a
yalnız ve yalnız
- öyle δ>0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; |x - a| < δ için.
Eğer g(x) a sayısına yeterince yakın x değerleri için sıfırdan farklı ise yukarıdaki iki tanım kullanılarak birleştirilebilir:
- f(x) O(g(x))dir;x
a
yalnız ve yalnız
iken.
Matematikte hem ∞ hem de a civarındaki asimptotikler kullanılır. ise sadece ∞a giden asimptotikler kullanılır. Ayrıca sadece pozitif değerli işlevler ele alındığından mutlak değer de kullanılmadan yazılabilir.
Örnek
Şu çokterimlilere bakalım:
f(x), O(g(x)) ya da O(x4) derecesindedir diyebiliriz. Tanıma göre, tüm x>1 değerleri için ve C bir sabit iken, |f(x)| ≤ C |g(x)| ifadesi geçerlidir.
İspat:
x > 1 iken
çünkü x3 < x4 ve devam eder.
Dikkat edilmesi gereken hususlar
Yukarıda bahsi geçen "f(x) O(g(x))dir" ifadesi genellikle f(x) = O(g(x)) şeklinde yazılır. Bu, gösterimin bir nebze kötüye kullanılması demektir. Elbette kastettiğimiz iki işlevin birbirine eşit olmaları değildir. O(g(x)) olma hali simetrik değildir:
fakat
.
Bu yüzden bazı yazarlar küme gösterimini tercih ederler ve f 
Ayrıca, aşağıdaki gibi bir "eşitlik"
"f(x) ile h(x)nin farkı O(g(x))dir" olarak anlaşılmalıdır.
Sık rastlanan işlev dereceleri
Aşağıda algoritma çözümlemesinde sıkça karşılaşılan işlev derecelerini görebilirsiniz. Tüm bunlar n sonsuza giderken durumunda belirtilmiştir. Daha yavaş büyüyen işlevler önce listelenmiştir. c keyfi bir sabit değerdir.
| gösterim | isim |
|---|---|
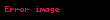 | sabit |
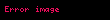 | |
 | logaritmik |
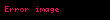 | |
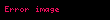 | |
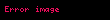 | |
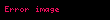 | (linearitmik), sözde doğrusal veya üst doğrusal |
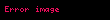 | |
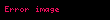 , , 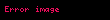 | çokterimli, bazen "cebirsel" de denir |
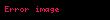 | , bazen "" de denir |
 | faktöriyel, bazen "kombinatoryel" de denir |
Pek sık rastlanmasa da, Büyük O gösterimi ile kullanılan çok daha hızlı büyüyen işlevler mevcuttur, mesela A(n,n) olarak temsil edilen Ackermann işlevinin tek değerli hâli. Bunun tam tersi çok yavaş büyüyen işlevler da vardır, ör. Ackermann işlevinin ters işlevi olan ve genellikle α(n) ile gösterilen işlev. Her ne kadar bu işlevler sınırsız olsa da pratik amaçlar için sabit çarpanlar olarak kabul edilirler.
Özellikler
Eğer bir f(n) işlevi diğer işlevlerin sonlu toplamı olarak yazılabiliyorsa o zaman bunların içinden en hızlı büyüyeni f(n) işlevinin derecesini belirler. Örneğin
.
Özel olarak eğer bir işlev n terimine bağlı birçokterimli tarafından üstten sınırlandırılabiliyorsa o zaman n değeri sonsuza gittikçe çokterimlinin düşük dereceli terimleri ihmal edilebilir.
O(nc) ve O(cn) çok farklıdır. İkincisi çok çok daha hızlı büyür ve c sabitinin değeri, bu değer 1 sayısından büyük olduğu sürece, bu durumu değiştirmez. n'nin herhangi bir kuvvetinden daha hızlı büyüyen bir işleve yüksek çokterimli (superpolynomial) denir. cn biçimindeki herhangi bir üssel işlevden daha yavaş büyüyen işleve ise altüssel denir. Bir algoritmanın zaman karmaşıklığı hem yüksek çokterimli hem de altüssel olabilir, bu tür algoritmalara örnek olarak bilinen en hızlı çarpanlara ayırma algoritmaları verilebilir.
O(log n) tam olarak O(log(nc)) ile aynıdır. Logaritmalar arasındaki fark sadece sabit değerden kaynaklanan farktır (çünkü log(nc)=c log n) ve bundan ötürü büyük O gösteriminde ihmal edilir. Benzer şekilde farklı tabanlara göre yazılmış logaritmalar da denk kabul edilir.
Çarpma
Toplama
Bir sabit ile çarpma
, k≠0
Bir sabit ile toplama
g(n) ∈ o(1) olmadığı takdirde ki bu durumda O(1)dir.
Diğer faydalı özellikler aşağıda belirtilmiştir.
İlişkili asimptotik gösterimler: O, o, Ω, ω, Θ, Õ
Büyük O işlevleri kıyaslamak için en sık kullanılan asimptotik gösterimdir ancak genellikle Θ yerine geçen resmi olmayan bir gösterim şeklidir (Theta, bk. aşağısı). Burada konuyla ilgili bazı gösterimleri "büyük O" cinsinden tanımlayacağız:
| Gösterim | Tanım | Matematiksel tanım |
|---|---|---|
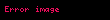 | asimptotik üst sınır |  |
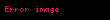 | asimptotik olarak ihmal edilebilir | 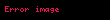 |
 | asimptotik alt sınır | 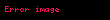 |
 | asimptotik baskın | 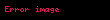 |
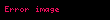 | asimptotik keskin sınır | 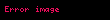 and and 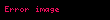 |
f(n) = o(g(n)) ilişkisi "f(n) g(n)nin küçük o'sudur" olarak okunur. Sezgisel olarak bunun anlamı şu demektir: g(n), f(n) işlevinden çok daha hızlı büyür. Biçimsel olarak söylemek gerekirse bu ifadenin anlamı şudur:
f(n)/g(n) ifadesinin limiti sıfırdır.
Büyük O gösterimi bir yana, Θ ve Ω sembolleri ile yapılan gösterim de bilgisayar bilimlerinde çok sık kullanılır. "Küçük o" daha ziyade matematikte kullanılır ve bilgisayar bilimlerinde kullanımı daha nadirdir. Küçük ω nadiren kullanılır.
Genelgeçer kullanımda O Θ kullanılması gereken yerlerde kullanılır, söz gelimi keskin bir sınır kastetildiğinde. Örneğin birisi "Yığın sıralaması ortalama durumda O(n log n)dir" diyebilir oysa asıl kastedilen "Yığın sıralaması ortalama durumda Θ(n log n)dir". Her iki ifade de doğru olmakla birlikte ikincisi daha güçlü bir iddiadır.
Bilgisayar bilimlerinde kullanılan bir başka sembol ise Õdir (Yumuşak-O olarak okunur). f(n) = Õ(g(n)) şeklindeki gösterim f(n) = O(g(n) logkg(n)) (bazı k değerleri için) için kısa yoldur. Temelde logaritmik çarpanları ihmal eden büyük O gösteriminden başka bir şey değildir. Bu gösterim daha çok algoritma başarımında "küçük kusurlar"ı belirlemeye yönelik başarım kestirimlerinde kullanılır (zira logkn, herhangi bir k sabiti için, daima o(n)'dir).
Büyük O ve küçük o
Aşağıdaki özellikleri bilmek faydalı olabilir:
- o(f) + o(f) ∈ o(f)
- o(f) o(g) ∈ o(fg)
- o(o(f)) ∈ o(f)
- o(f) ∈ O(f) (ve dolayısıyla yukarıdaki özellikler o ve O ile kombinasyonların çoğuna uygulanabilir).
Çoklu değişkenler
Büyük O (ve küçük o ve Ω...) birden çok değişken için de kullanılabilir. Örneğin,
ifadesine göre öyle C ve N sabitleri vardır ki
Çift anlamlılığı engellemek için hangi değişkenin esas kabul edildiği daima belirtilmelidir çünkü
ifadesi,
ifadesinden çok farklıdır.
Kaynakça
- Marian Slodička. Mathematical Analysis I. University of Ghent, 2003.
- Donald Knuth. The Art of Computer Programming, Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. . Section 1.2.11: Asymptotic Representations, pp. 107–123.
- , , , and . , Second Edition. MIT Press and McGraw-Hill, 2001. . Section 3.1: Asymptotic notation, pp. 41–50.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Buyuk O Big Oh gosterimi matematiksel bir gosterim olup islevlerin fonksiyonlarin davranislarini tarif etmek icin kullanilir Bir islevin buyumesinin asimptotik ust sinirini daha basit baska bir islev cinsinden tanimlanmasi demektir Iki temel uygulama alani vardir matematik alaninda genellikle kirpilmis bir sonsuz serinin kalan terimini karakterize etmek icin kullanilir bilgisayar bilimlerinde ise algoritmalarin bilgi islemsel karmasikliginin icin kullanilir Buyuk O gosterimi ornegi f x O g x Bu gosterim ilk olarak Alman sayilar kuramcisi tarafindan 1892 yilinda yazdigi Analytische Zahlentheorie kitabinda kullanilmistir Gosterim bir baska Alman matematikci olan Edmund Landau tarafindan yaygin kullanima sokulmustur bundan oturu bazen olarak da anilir Buyuk O Ingiliz dilindeki order of yani bir seyin derecesi anlamina gelen soz obegini hatirlatmak amaci ile kullaniliyordu ve ilk olarak buyuk harfi idi gunumuzde buyuk O kullanilmakta ve 0 sayisi hic kullanilmamaktadir Kullanim alanlariBu gosterimin bicimsel olarak yakin ama temelde farkli iki kullanimi vardir sonsuz ve asimptotikler Bu ayrim sadece uygulamadadir ancak buyuk O nun bicimsel tanimi her iki durumda ayni olup islev argumaninin limitleri degismektedir Sonsuz asimptotikler Buyuk O gosterimi faydalidir Soz gelimi n boyundaki bir problemi cozmek icin gereken zaman adim sayisi T n 4n 2n 2 olarak bulunabilir n buyudukce n terimi o kadar hizli buyuyecektir ki diger terimlerin buyume hizi buna kiyasla ihmal edilebilecek kadar dusuk kalacaktir ornegin n 500 icin 4n terimi 2n teriminin 1000 kati buyuklugunde olacaktir ve dolayisiyla bu ikinci terimin degeri tum ifadenin degerini belirlemede cogu amac bakimindan ihmal edilebilir bir etkiye sahip olacaktir Buna ek olarak ayni ifadeyi n veya 2n terimleri iceren bir ifade ile kiyaslayacak olursak katsayilar da anlamlarini yitirecektir T n 1 000 000n ve U n n olsa bile ikinci ifade n 1 000 000 u gectikce birinci ifadeye kiyasla daima daha buyuk olacaktir T 1 000 000 1 000 000 U 1 000 000 O halde Buyuk O gosterimi isin ozunu sade bicimde sunmaktadir su sekilde yazabilir T n O n2 displaystyle T n in O n 2 ve algoritmanin n2 dereceden zaman karmasikligina sahip oldugunu soyleyebiliriz Sonsuz kucuk asimptotikler Buyuk O ayni zamanda bir matematiksel islev icin gelistirilen yaklasik islevin hata terimini tarif etmek icin de kullanilabilir Ornegin ex 1 x x2 2 O x3 x 0 iken displaystyle e x 1 x x 2 2 hbox O x 3 hbox x to 0 hbox hbox iken ifadesi hatanin yani ex 1 x x2 2 displaystyle e x 1 x x 2 2 farkinin mutlak deger bakimindan sifira yeterince yakin x degerleri icin bir sabit carpi x3 degerinden daha kucuk oldugunu belirtir Bicimsel tanimf x ve g x gercel sayilar kumesinin bir alt kumesi uzerinde tanimlanmis iki islev olsun Bu durumda deriz ki f x O g x dir x displaystyle to yalniz ve yalniz oyle x0 ve M sayilari varsa ki f x M g x x gt x0 icin Ayni gosterim f islevinin bir a gercel sayisi civarindaki davranisini tarif etmek icin de kullanilabilir Deriz ki f x O g x dir x displaystyle to a yalniz ve yalniz oyle d gt 0 ve M sayilari varsa ki f x M g x x a lt d icin Eger g x a sayisina yeterince yakin x degerleri icin sifirdan farkli ise yukaridaki iki tanim kullanilarak birlestirilebilir f x O g x dir x displaystyle to a yalniz ve yalniz lim supx a f x g x lt displaystyle limsup x to a left frac f x g x right lt infty iken Matematikte hem hem de a civarindaki asimptotikler kullanilir ise sadece a giden asimptotikler kullanilir Ayrica sadece pozitif degerli islevler ele alindigindan mutlak deger de kullanilmadan yazilabilir OrnekSu cokterimlilere bakalim f x 6x4 2x3 5 displaystyle f x 6x 4 2x 3 5 g x x4 displaystyle g x x 4 f x O g x ya da O x4 derecesindedir diyebiliriz Tanima gore tum x gt 1 degerleri icin ve C bir sabit iken f x C g x ifadesi gecerlidir Ispat 6x4 2x3 5 6x4 2x3 5 displaystyle 6x 4 2x 3 5 leq 6x 4 2x 3 5 x gt 1 iken 6x4 2x3 5 6x4 2x4 5x4 displaystyle 6x 4 2x 3 5 leq 6x 4 2x 4 5x 4 cunku x3 lt x4 ve devam eder 6x4 2x3 5 13x4 displaystyle 6x 4 2x 3 5 leq 13x 4 6x4 2x3 5 13 x4 displaystyle 6x 4 2x 3 5 leq 13 x 4 Dikkat edilmesi gereken hususlarYukarida bahsi gecen f x O g x dir ifadesi genellikle f x O g x seklinde yazilir Bu gosterimin bir nebze kotuye kullanilmasi demektir Elbette kastettigimiz iki islevin birbirine esit olmalari degildir O g x olma hali simetrik degildir O x O x2 displaystyle mbox O x mbox O x 2 fakat O x2 O x displaystyle mbox O x 2 neq mbox O x Bu yuzden bazi yazarlar kume gosterimini tercih ederler ve f displaystyle in O g yazarlar bunu yaparken de O g yi g islevinin altinda kalan tum islevlerin kumesi olarak dusunurler Ayrica asagidaki gibi bir esitlik f x h x O g x displaystyle f x h x mbox O g x f x ile h x nin farki O g x dir olarak anlasilmalidir Sik rastlanan islev dereceleriAsagida algoritma cozumlemesinde sikca karsilasilan islev derecelerini gorebilirsiniz Tum bunlar n sonsuza giderken durumunda belirtilmistir Daha yavas buyuyen islevler once listelenmistir c keyfi bir sabit degerdir gosterim isimO 1 displaystyle O 1 sabitO log n displaystyle O log n O log n displaystyle O log n logaritmikO log n c displaystyle O log n c o n displaystyle o n O n displaystyle O n O nlog n displaystyle O n log n linearitmik sozde dogrusal veya ust dogrusalO n2 displaystyle O n 2 O nc displaystyle O n c c gt 1 displaystyle c gt 1 cokterimli bazen cebirsel de denirO cn displaystyle O c n bazen de denirO n displaystyle O n faktoriyel bazen kombinatoryel de denir Pek sik rastlanmasa da Buyuk O gosterimi ile kullanilan cok daha hizli buyuyen islevler mevcuttur mesela A n n olarak temsil edilen Ackermann islevinin tek degerli hali Bunun tam tersi cok yavas buyuyen islevler da vardir or Ackermann islevinin ters islevi olan ve genellikle a n ile gosterilen islev Her ne kadar bu islevler sinirsiz olsa da pratik amaclar icin sabit carpanlar olarak kabul edilirler OzelliklerEger bir f n islevi diger islevlerin sonlu toplami olarak yazilabiliyorsa o zaman bunlarin icinden en hizli buyuyeni f n islevinin derecesini belirler Ornegin f n 10log n 5 log n 3 7n 3n2 6n3 O n3 displaystyle f n 10 log n 5 log n 3 7n 3n 2 6n 3 in hbox O n 3 Ozel olarak eger bir islev n terimine bagli bircokterimli tarafindan ustten sinirlandirilabiliyorsa o zaman n degeri sonsuza gittikce cokterimlinin dusuk dereceli terimleri ihmal edilebilir O nc ve O cn cok farklidir Ikincisi cok cok daha hizli buyur ve c sabitinin degeri bu deger 1 sayisindan buyuk oldugu surece bu durumu degistirmez n nin herhangi bir kuvvetinden daha hizli buyuyen bir isleve yuksek cokterimli superpolynomial denir cn bicimindeki herhangi bir ussel islevden daha yavas buyuyen isleve ise altussel denir Bir algoritmanin zaman karmasikligi hem yuksek cokterimli hem de altussel olabilir bu tur algoritmalara ornek olarak bilinen en hizli carpanlara ayirma algoritmalari verilebilir O log n tam olarak O log nc ile aynidir Logaritmalar arasindaki fark sadece sabit degerden kaynaklanan farktir cunku log nc c log n ve bundan oturu buyuk O gosteriminde ihmal edilir Benzer sekilde farkli tabanlara gore yazilmis logaritmalar da denk kabul edilir Carpma O f n O g n O f n g n displaystyle O f n O g n O f n g n Toplama O f n O g n O max f n g n displaystyle O f n O g n O max lbrace f n g n rbrace Bir sabit ile carpma O kg n O g n displaystyle O kg n O g n k 0Bir sabit ile toplama O k g n O g n displaystyle O k g n O g n g n o 1 olmadigi takdirde ki bu durumda O 1 dir Diger faydali ozellikler asagida belirtilmistir Iliskili asimptotik gosterimler O o W w 8 OBuyuk O islevleri kiyaslamak icin en sik kullanilan asimptotik gosterimdir ancak genellikle 8 yerine gecen resmi olmayan bir gosterim seklidir Theta bk asagisi Burada konuyla ilgili bazi gosterimleri buyuk O cinsinden tanimlayacagiz Gosterim Tanim Matematiksel tanimf n O g n displaystyle f n in O g n asimptotik ust sinir limx f x g x lt displaystyle lim x to infty left frac f x g x right lt infty f n o g n displaystyle f n in o g n asimptotik olarak ihmal edilebilir limx f x g x 0 displaystyle lim x to infty frac f x g x 0 f n W g n displaystyle f n in Omega g n asimptotik alt sinir limx f x g x gt 0 displaystyle lim x to infty left frac f x g x right gt 0 f n w g n displaystyle f n in omega g n asimptotik baskin limx g x f x 0 displaystyle lim x to infty frac g x f x 0 f n 8 g n displaystyle f n in Theta g n asimptotik keskin sinir f O g displaystyle f in O g and g O f displaystyle g in O f f n o g n iliskisi f n g n nin kucuk o sudur olarak okunur Sezgisel olarak bunun anlami su demektir g n f n islevinden cok daha hizli buyur Bicimsel olarak soylemek gerekirse bu ifadenin anlami sudur f n g n ifadesinin limiti sifirdir Buyuk O gosterimi bir yana 8 ve W sembolleri ile yapilan gosterim de bilgisayar bilimlerinde cok sik kullanilir Kucuk o daha ziyade matematikte kullanilir ve bilgisayar bilimlerinde kullanimi daha nadirdir Kucuk w nadiren kullanilir Genelgecer kullanimda O 8 kullanilmasi gereken yerlerde kullanilir soz gelimi keskin bir sinir kastetildiginde Ornegin birisi Yigin siralamasi ortalama durumda O n log n dir diyebilir oysa asil kastedilen Yigin siralamasi ortalama durumda 8 n log n dir Her iki ifade de dogru olmakla birlikte ikincisi daha guclu bir iddiadir Bilgisayar bilimlerinde kullanilan bir baska sembol ise Odir Yumusak O olarak okunur f n O g n seklindeki gosterim f n O g n logkg n bazi k degerleri icin icin kisa yoldur Temelde logaritmik carpanlari ihmal eden buyuk O gosteriminden baska bir sey degildir Bu gosterim daha cok algoritma basariminda kucuk kusurlar i belirlemeye yonelik basarim kestirimlerinde kullanilir zira logkn herhangi bir k sabiti icin daima o n dir Buyuk O ve kucuk oAsagidaki ozellikleri bilmek faydali olabilir o f o f o f o f o g o fg o o f o f o f O f ve dolayisiyla yukaridaki ozellikler o ve O ile kombinasyonlarin coguna uygulanabilir Coklu degiskenlerBuyuk O ve kucuk o ve W birden cok degisken icin de kullanilabilir Ornegin f n m n2 m3 O n m as n m displaystyle f n m n 2 m 3 hbox O n m mbox as n m to infty ifadesine gore oyle C ve N sabitleri vardir ki n m gt N f n m n2 m3 n m C displaystyle forall n m gt N f n m leq n 2 m 3 n m C Cift anlamliligi engellemek icin hangi degiskenin esas kabul edildigi daima belirtilmelidir cunku f n m O nm as n m displaystyle f n m hbox O n m mbox as n m to infty ifadesi m f n m O nm as n displaystyle forall m f n m hbox O n m mbox as n to infty ifadesinden cok farklidir KaynakcaMarian Slodicka Mathematical Analysis I University of Ghent 2003 Donald Knuth The Art of Computer Programming Volume 1 Fundamental Algorithms Third Edition Addison Wesley 1997 ISBN 0 201 89683 4 Section 1 2 11 Asymptotic Representations pp 107 123 and Second Edition MIT Press and McGraw Hill 2001 ISBN 0 262 03293 7 Section 3 1 Asymptotic notation pp 41 50
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans