Düzgün olmayan rasyonel temelli eğri (İngilizce Non-uniform rational basis spline, NURBS), eğrileri ve yüzeyleri oluşturmak ve temsil etmek için bilgisayar grafiklerinde yaygın olarak kullanılan matematiksel bir modeldir. Hem analitik (ortak matematiksel formüllerle tanımlanan yüzeyler) hem de modellenmiş şekilleri işlemek için büyük esneklik ve hassasiyet sunar. NURBS yaygın olarak bilgisayar destekli tasarım (CAD ), imalat (CAM ) ve mühendislikte (CAE ) kullanılır ve IGES, STEP, ACIS ve PHIGS gibi çok sayıda endüstri çapında standardın parçasıdır . NURBS araçları ayrıca çeşitli 3B modelleme ve animasyon yazılım paketlerinde de bulunur. NURBS yüzeyleri, üç boyutlu uzayda bir yüzeye eşlenen iki parametrenin işlevleridir. Yüzeyin şekli kontrol noktaları ile belirlenir. NURBS yüzeyleri, kompakt bir biçimde basit geometrik şekilleri temsil edebilir. T-spline'lar ve alt bölme yüzeyleri, NURBS yüzeylerine kıyasla kontrol noktalarının sayısını iki kat azalttığı için karmaşık organik şekiller için daha uygundur. NURBS eğrilerini ve yüzeylerini düzenlemek oldukça sezgisel ve öngörülebilirdir. Kontrol noktaları her zaman doğrudan eğriye / yüzeye bağlanır veya bir lastik bantla bağlanmış gibi davranır. Kullanıcı arayüzünün türüne bağlı olarak, düzenleme, Bézier eğrileri için en açık ve yaygın olan bir elemanın kontrol noktaları aracılığıyla veya spline modelleme veya hiyerarşik düzenleme gibi daha yüksek seviyeli araçlar aracılığıyla gerçekleştirilebilir.

Tarih

Bilgisayarlardan önce tasarımlar çeşitli çizim araçlarıyla kağıt üzerine elle çizilirdi . Cetveller düz çizgiler, kullanıldı pergel çevreler için ve protractors açılar için. Ancak bir geminin pruvasının serbest biçimli eğrisi gibi birçok şekil bu aletlerle çizilemezdi. Bu tür eğriler çekim tahtasında serbestçe çizilebilmesine rağmen, gemi yapımcıları genellikle elle yapılamayacak gerçek boyutlu bir versiyona ihtiyaç duyuyordu. Bu tür büyük çizimler, spline adı verilen esnek ahşap şeritlerin yardımıyla yapıldı. Spline'lar, "ördekler" adı verilen önceden belirlenmiş birkaç noktada yerinde tutuldu; ördekler arasında, yivli malzemenin esnekliği, şeridin bükülme enerjisini en aza indiren şekli almasına neden oldu, böylece kısıtlamalara uyan mümkün olan en pürüzsüz şekli oluşturdu. Ördekler hareket ettirilerek şekil ayarlanabilir.
1946'da matematikçiler spline şeklini incelemeye başladılar ve spline eğrisi veya spline fonksiyonu olarak bilinen parçalı polinom formülü türettiler. IJ Schoenberg, teknik ressamlar tarafından kullanılan mekanik eğriye benzerliğinden sonra spline işlevine adını verdi.
Bilgisayarlar tasarım sürecine dahil edilirken, bu tür eğrilerin fiziksel özellikleri, matematiksel hassasiyetle modellenebilmeleri ve gerektiğinde yeniden üretilebilmeleri için araştırıldı. Fransa'da Renault mühendisi Pierre Bézier ve Citroën'in fizikçi ve matematikçisi Paul de Casteljau öncü çalışmalar yaptı. Birbirlerine neredeyse paralel çalıştılar, ancak Bézier çalışmasının sonuçlarını yayınladığı için, Bézier eğrilerine onun adı verilirken, de Casteljau'nun adı yalnızca ilgili algoritmalarla ilişkilendirildi.
Başlangıçta NURBS sadece otomobil şirketlerinin tescilli CAD paketlerinde kullanılıyordu. Daha sonra standart bilgisayar grafik paketlerinin bir parçası oldular.
NURBS eğrilerinin ve yüzeylerinin gerçek zamanlı, etkileşimli olarak oluşturulması ilk olarak 1989'da Silicon Graphics iş istasyonlarında ticari olarak sağlandı. 1993 yılında, NöRBS adı verilen PC'ler için ilk etkileşimli NURBS modelleyicisi, Berlin Teknik Üniversitesi ile işbirliği yapan küçük bir başlangıç şirketi olan CAS Berlin tarafından geliştirildi.
Süreklilik
Yapım aşamasında olan bir yüzey, örneğin bir motorlu yatın gövdesi, genellikle yama olarak bilinen birkaç NURBS yüzeyinden oluşur. Bu yamalar, sınırlar görünmeyecek şekilde birbirine takılmalıdır. Bu, matematiksel olarak geometrik süreklilik kavramı ile ifade edilir.
NURBS'nin farklı seviyelerde geometrik süreklilik oluşturma ve kurma becerisinden yararlanan daha yüksek seviyeli araçlar mevcuttur:
- Konumsal süreklilik (G 0 ), iki eğrinin veya yüzeyin son konumları çakıştığı zaman geçerlidir. Eğriler veya yüzeyler yine de bir açıyla birleşerek keskin bir köşe veya kenara yol açabilir ve kırılmış vurgulara neden olabilir.
- Teğetsel süreklilik (G¹), eğrilerin veya yüzeylerin uç vektörlerinin paralel olmasını ve keskin kenarları ekarte ederek aynı şekilde işaret etmesini gerektirir. Teğet olarak sürekli bir kenara düşen vurgular her zaman süreklidir ve bu nedenle doğal göründüğünden, bu süreklilik düzeyi çoğu zaman yeterli olabilir.
- Eğrilik sürekliliği (G²) ayrıca uç vektörlerin aynı uzunlukta ve uzunluk değişim hızında olmasını gerektirir. Sürekli eğrilikli bir kenara düşen parlak noktalar herhangi bir değişiklik göstermez ve iki yüzeyin tek olarak görünmesine neden olur. Bu görsel olarak "mükemmel derecede pürüzsüz" olarak tanınabilir. Bu süreklilik düzeyi, tek bir sürekli yüzey oluşturan birçok iki kübik yama gerektiren modellerin oluşturulmasında çok kullanışlıdır.
Geometrik süreklilik esas olarak ortaya çıkan yüzeyin şeklini ifade eder; NURBS yüzeyleri fonksiyonlar olduğundan, yüzeyin türevlerini parametrelere göre tartışmak da mümkündür. Bu, parametrik süreklilik olarak bilinir. Belirli bir derecenin parametrik sürekliliği, o derecenin geometrik sürekliliğini ifade eder.
Birinci ve ikinci düzey parametrik süreklilik (C 0 ve C¹), pratik amaçlar için konumsal ve teğetsel (G 0 ve G¹) süreklilikle aynıdır. Bununla birlikte, üçüncü düzey parametrik süreklilik (C²), parametrelendirmesinin de sürekli olması nedeniyle eğrilik sürekliliğinden farklıdır. Uygulamada, tek tip B-spline'lar kullanılırsa C² sürekliliği elde etmek daha kolaydır.
C n sürekliliğinin tanımı, bitişik eğrilerin / yüzeylerin n inci türevinin (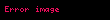
Parlak noktalar ve yansımalar, en azından G² sürekliliğine sahip NURBS yüzeyleri olmadan elde edilmesi pratik olarak imkansız olan mükemmel düzleştirmeyi ortaya çıkarabilir. Bu aynı ilke, yüzey değerlendirme yöntemlerinden biri olarak kullanılır; bu yöntemle, üzerine yansıyan beyaz şeritlere sahip bir yüzeyin ışın izlemeli veya yansıma haritalanmış bir görüntüsü, bir yüzey veya bir dizi yüzey üzerindeki en küçük sapmaları bile gösterecektir. Bu yöntem, araba yüzeyindeki neon ışıklı tavanın yansımalarının kalitesinin kontrol edilmesiyle yüzey kalitesinin denetlendiği otomobil prototiplemesinden türetilmiştir. Bu yöntem aynı zamanda "Zebra analizi" olarak da bilinir.
Teknik özellikler

Bir NURBS eğrisi, sırası, bir dizi ağırlıklı kontrol noktası ve bir düğüm vektörü ile tanımlanır. NURBS eğrileri ve yüzeyleri, hem B-spline'ların hem de Bézier eğrilerinin ve yüzeylerinin genelleştirmeleridir; birincil fark, NURBS eğrilerini rasyonel kılan kontrol noktalarının ağırlıklandırılmasıdır. (Sigara rasyonel bir deyişle, basit, B-spline her kontrol noktası normal homojen olmayan yerine daha [ 'w' no] koordinat oransal B-spline özel bir durum / alt küme vardır homojen koordinat. Bu, her kontrol noktasında "1" ağırlığa sahip olmaya eşdeğerdir; Rasyonel B-spline bir ağırlık olarak her bir kontrol noktasının 'w' kullanın. ) İki boyutlu kontrol noktaları ızgarası kullanılarak, düzlemsel yamalar ve kürelerin bölümleri dahil NURBS yüzeyleri oluşturulabilir. Bunlar iki değişkenle parametrelendirilir (tipik olarak s ve t veya u ve v olarak adlandırılır). Bu, NURBS haritalaması oluşturmak için rastgele boyutlara genişletilebilir 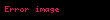
NURBS eğrileri ve yüzeyleri birkaç nedenden dolayı kullanışlıdır: -
- Belirli bir sıra için NURBS kümesi, afin dönüşümler altında değişmez : döndürme ve öteleme gibi işlemler, NURBS eğrilerine ve yüzeylerine, kontrol noktalarına uygulanarak uygulanabilir.
- Hem standart analitik şekiller (ör. Konikler ) hem de serbest biçimli şekiller için ortak bir matematiksel form sunarlar.
- Çok çeşitli şekiller tasarlama esnekliği sağlarlar.
- Şekilleri depolarken bellek tüketimini azaltırlar (daha basit yöntemlere kıyasla).
- Sayısal olarak kararlı ve doğru algoritmalarla oldukça hızlı bir şekilde değerlendirilebilirler.
Sonraki bölümlerde, NURBS tek boyutta (eğriler) tartışılmaktadır. Hepsi iki veya daha fazla boyuta genellenebilir.
NURBS eğrisinin kuvveti
Bir NURBS eğrisinin kuvveti, eğri üzerindeki herhangi bir noktayı etkileyen yakın kontrol noktalarının sayısını tanımlar. Eğri, matematiksel olarak eğrinin mertebesinden bir dereceden daha düşük bir polinom ile temsil edilir. Bu nedenle, ikinci dereceden eğrilere (doğrusal polinomlarla temsil edilenler) doğrusal eğriler, üçüncü dereceden eğrilere ikinci dereceden eğriler ve dördüncü dereceden eğrilere kübik eğriler denir. Kontrol noktalarının sayısı eğrinin kuvvetinden büyük veya ona eşit olmalıdır.
Pratikte, kübik eğriler en sık kullanılanlardır. Beşinci ve altıncı mertebeden eğriler bazen, özellikle sürekli yüksek mertebeden türevler elde etmek için kullanışlıdır, ancak daha yüksek mertebeden eğriler pratikte hiçbir zaman kullanılmaz, çünkü bunlar dahili sayısal problemlere yol açar ve orantısız şekilde büyük hesaplama süreleri gerektirme eğilimindedirler.
Kontrol noktaları

Kontrol noktaları, eğrinin şeklini belirler. Tipik olarak, eğrinin her noktası, bir dizi kontrol noktasının ağırlıklı toplamı alınarak hesaplanır. Her bir noktanın ağırlığı, geçerli parametreye göre değişir. D derecelik bir eğri için, herhangi bir kontrol noktasının ağırlığı, parametre uzayının d + 1 aralıklarında yalnızca sıfırdan farklıdır. Bu aralıklar içinde ağırlık, d derecesinin bir polinom fonksiyonuna (temel fonksiyonlar) göre değişir. Aralıkların sınırlarında, temel fonksiyonlar sorunsuz bir şekilde sıfıra gider, pürüzsüzlük polinomun derecesine göre belirlenir.
Örnek olarak, birinci derecenin temel işlevi bir üçgen işlevidir. Sıfırdan bire yükselir, sonra tekrar sıfıra düşer. Yükselirken, önceki kontrol noktasının temel işlevi düşer. Bu şekilde, eğri iki nokta arasında interpolasyon yapar ve ortaya çıkan eğri, aralıklı sınırlarda veya düğümlerde türevlenemeyen, sürekli olan bir çokgendir. Daha yüksek dereceli polinomlar buna bağlı olarak daha sürekli türevlere sahiptir. Aralık içinde temel fonksiyonların polinom doğasının ve yapının doğrusallığının eğriyi mükemmel bir şekilde pürüzsüz hale getirdiğine dikkat edin, bu nedenle süreksizlik sadece düğümlerde ortaya çıkabilir.
Pek çok uygulamada, tek bir kontrol noktasının yalnızca aktif olduğu aralıkları etkilemesi, yerel destek olarak bilinen oldukça istenen bir özelliktir. Modellemede, bir yüzeyin bir kısmının değiştirilmesine izin verirken diğer kısımların değişmeden kalmasına izin verir.
Daha fazla kontrol noktası eklemek, belirli bir eğriye daha iyi yaklaşıma izin verir, ancak yalnızca belirli bir eğri sınıfı tam olarak sınırlı sayıda kontrol noktasıyla temsil edilebilir. NURBS eğrileri ayrıca her kontrol noktası için bir skaler ağırlık içerir . Bu, kontrol noktalarının sayısını gereksiz yere yükseltmeden eğrinin şekli üzerinde daha fazla kontrole izin verir. Özellikle, tam olarak temsil edilebilen eğriler kümesine daire ve elips gibi konik bölümler ekler. NURBS'deki rasyonel terimi bu ağırlıkları ifade eder.
Kontrol noktaları herhangi bir boyutluluğa sahip olabilir. Tek boyutlu noktalar sadece parametrenin skaler bir fonksiyonunu tanımlar. Bunlar genellikle parlaklığı ve renk eğrilerini ayarlamak için görüntü işleme programlarında kullanılır. Üç boyutlu kontrol noktaları, 3B uzayda bir konum olan 'nokta' kelimesinin günlük anlamında kullanıldığı 3B modellemede bolca kullanılır. Çok boyutlu noktalar, bir robot kolunun farklı konumsal ve dönme ayarları gibi zamana bağlı değer kümelerini kontrol etmek için kullanılabilir. NURBS yüzeyleri bunun sadece bir uygulamasıdır. Her kontrol 'noktası' aslında bir eğri tanımlayan tam bir kontrol noktaları vektörüdür. Bu eğriler, derecelerini ve kontrol noktalarının sayısını paylaşır ve parametre uzayının bir boyutunu kapsar. Bu kontrol vektörlerinin parametre uzayının diğer boyutu üzerinde enterpolasyonuyla, yüzeyi tanımlayan sürekli bir eğri seti elde edilir.
Düğüm vektör
Düğüm vektörü, kontrol noktalarının NURBS eğrisini nerede ve nasıl etkilediğini belirleyen bir parametre değerleri dizisidir. Düğüm sayısı her zaman kontrol noktalarının sayısı artı eğri derecesi artı birdir (yani kontrol noktalarının sayısı artı eğri sırası). Düğüm vektörü, parametrik alanı daha önce bahsedilen aralıklarla böler, genellikle düğüm aralıkları olarak anılır. Parametre değeri yeni bir düğüm aralığına her girdiğinde, yeni bir kontrol noktası aktif hale gelirken, eski bir kontrol noktası atılır. Düğüm vektöründeki değerlerin azalan sırada olması gerektiği, dolayısıyla (0, 0, 1, 2, 3, 3) geçerliyken (0, 0, 2, 1, 3, 3) geçerli değildir.
Ardışık düğümler aynı değere sahip olabilir. Bu daha sonra sıfır uzunlukta bir düğüm aralığını tanımlar, bu da iki kontrol noktasının aynı anda etkinleştirildiğini (ve tabii ki iki kontrol noktasının devre dışı bırakıldığını) gösterir. Bunun, ortaya çıkan eğrinin veya daha yüksek türevlerinin sürekliliği üzerinde etkisi vardır; örneğin, başka türlü pürüzsüz bir NURBS eğrisinde köşelerin oluşturulmasına izin verir. Çakışan düğüm bir dizi bazen belirli bir çoğu ile bir düğüm olarak adlandırılır. Çokluğu iki veya üç olan düğümler, çift veya üçlü düğüm olarak bilinir. Bir düğümün çokluğu, eğrinin derecesiyle sınırlıdır; çünkü daha yüksek bir çokluk eğriyi ayrık parçalara böler ve kontrol noktalarını kullanılmadan bırakır. Birinci derece NURBS için, her düğüm bir kontrol noktası ile eşleştirilir.
Düğüm vektörü genellikle sıraya eşit çokluğa sahip bir düğümle başlar. Bu mantıklıdır, çünkü bu, ilk düğüm aralığı üzerinde etkisi olan kontrol noktalarını etkinleştirir. Benzer şekilde, düğüm vektörü genellikle bu çokluğun bir düğümü ile biter. Bu tür düğüm vektörlerine sahip eğriler bir kontrol noktasında başlar ve biter.
Düğümlerin değerleri, giriş parametresi ile karşılık gelen NURBS değeri arasındaki eşleşmeyi kontrol eder. Örneğin, bir NURBS, zaman içinde uzayda bir yolu tanımlıyorsa, düğümler, işlevin kontrol noktalarından sonra ilerlediği zamanı kontrol eder. Bununla birlikte, şekilleri temsil etme amaçları için, yalnızca düğüm değerleri arasındaki farkın oranları önemlidir; bu durumda düğüm vektörleri (0, 0, 1, 2, 3, 3) ve (0, 0, 2, 4, 6, 6) aynı eğriyi üretir. Düğüm değerlerinin pozisyonları, parametre uzayının eğri uzayıyla eşleştirilmesini etkiler. Bir NURBS eğrisinin oluşturulması, genellikle parametre aralığında sabit bir adımla adımlanarak yapılır. Düğüm aralığı uzunlukları değiştirilerek, eğriliğin yüksek olduğu bölgelerde daha fazla numune noktası kullanılabilir. Diğer bir kullanım, parametre değerinin bir miktar fiziksel öneme sahip olduğu durumlarda, örneğin parametre zaman ise ve eğri bir robot kolunun hareketini tanımlıyorsa. Düğüm aralığı uzunlukları daha sonra, robot koluna veya çevresine zarar gelmesini önlemek için doğru olmak için gerekli olan hız ve ivmeye dönüşür. Haritalamadaki bu esneklik, NURBS'deki tek tip olmayan ifadesinin kastettiği şeydir.
Yalnızca dahili hesaplamalar için gerekli olan düğümler genellikle modelleme yazılımı kullanıcıları için yararlı değildir. Bu nedenle, birçok modelleme uygulaması düğümleri düzenlenebilir ve hatta görünür hale getirmez. Kontrol noktalarındaki varyasyona bakarak makul düğüm vektörleri oluşturmak genellikle mümkündür. NURBS yazılımının daha yeni sürümleri (örneğin, Autodesk Maya ve Rhinoceros 3D ) düğüm konumlarının etkileşimli olarak düzenlenmesine izin verir, ancak bu, kontrol noktalarının düzenlenmesinden önemli ölçüde daha az sezgiseldir.
Temel fonksiyonların oluşturulması
NURBS eğrilerinin oluşturulmasında kullanılan B-spline temel fonksiyonları genellikle şu şekilde belirtilir: 



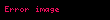

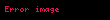
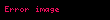




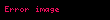

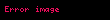 (mavi) ve
(mavi) ve  (yeşil) (üstte), ağırlık fonksiyonları
(yeşil) (üstte), ağırlık fonksiyonları  ve
ve  (orta) ve ortaya çıkan ikinci dereceden temel işlevi (alt). Düğümler 0, 1, 2 ve 2,5
(orta) ve ortaya çıkan ikinci dereceden temel işlevi (alt). Düğümler 0, 1, 2 ve 2,5



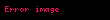





ve
Fonksiyonlar 



Yine tümevarımla, parametrenin belirli bir değeri için temel fonksiyonların toplamının birlik olduğu kanıtlanabilir. Bu, temel işlevlerin birlik özelliğinin bölümü olarak bilinir.
Şekiller, {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1, düğümler için doğrusal ve ikinci dereceden temel fonksiyonları gösterir. . . }
Bir düğüm aralığı diğerlerinden oldukça kısadır. Bu düğüm aralığında, ikinci dereceden temel fonksiyonundaki tepe daha belirgindir ve neredeyse bire ulaşır. Tersine, bitişik temel işlevler daha hızlı sıfıra düşer. Geometrik yorumlamada bu, eğrinin karşılık gelen kontrol noktasına yakından yaklaştığı anlamına gelir. Çift düğüm durumunda düğüm açıklığının uzunluğu sıfır olur ve tepe tam olarak bire ulaşır. Temel işlev artık bu noktada farklılaştırılamaz. Komşu kontrol noktaları eşdoğrusal değilse eğri keskin bir köşeye sahip olacaktır.
NURBS eğrisinin genel formu
Temel fonksiyonların tanımlarını kullanma 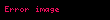
Bunda, 


rasyonel temel işlevler olarak bilinir.
NURBS yüzeyinin genel formu
İki NURBS eğrisinin tensör ürünü olarak bir NURBS yüzeyi elde edilir, böylece iki bağımsız parametre kullanılır. 


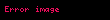
ile
rasyonel temel işlevler olarak.
NURBS nesnelerini düzenleme

Bir NURBS nesnesine bir dizi dönüşüm uygulanabilir. Örneğin, bazı eğri belirli bir derece ve N kontrol noktası kullanılarak tanımlanırsa, aynı eğri aynı derece ve N + 1 kontrol noktaları kullanılarak ifade edilebilir. İşlemde bir dizi kontrol noktası pozisyon değiştirir ve düğüm vektörüne bir düğüm eklenir. Bu manipülasyonlar, etkileşimli tasarım sırasında yoğun bir şekilde kullanılır. Bir kontrol noktası eklerken, eğrinin şekli aynı kalmalı ve sonraki ayarlamalar için başlangıç noktası oluşturmalıdır. Bu işlemlerden birkaçı aşağıda tartışılmaktadır.
Düğüm ekleme
Terimden de anlaşılacağı gibi, düğüm ekleme, düğüm vektörüne bir düğüm ekler. Eğrinin derecesi ise 


Bir düğüm, düğümün maksimum çokluğuna kadar birden çok kez eklenebilir. Bu bazen düğüm iyileştirme olarak adlandırılır ve tekrarlanan düğüm eklemeden daha verimli olan bir algoritma ile elde edilebilir.
Düğüm çıkarma
Düğüm çıkarma, düğüm atmanın tersidir. Amacı, daha kompakt bir görünüm elde etmek için düğümleri ve ilgili kontrol noktalarını kaldırmaktır. Açıktır ki, eğrinin tam şeklini korurken bu her zaman mümkün değildir. Pratikte, bir düğümün kaldırılıp kaldırılamayacağını belirlemek için doğrulukta bir tolerans kullanılır. İşlem, kontrol noktalarının manuel olarak eklenmiş olabileceği etkileşimli bir oturumdan sonra veya basit bir dönüştürme işleminin gereksiz kontrol noktalarına yol açtığı farklı bir temsilden bir eğri içe aktarıldıktan sonra temizlemek için kullanılır.
Derece yükselmesi
Belirli bir derecedeki bir NURBS eğrisi, her zaman daha yüksek dereceli bir NURBS eğrisi ile temsil edilebilir. Bu, ayrı NURBS eğrilerini birleştirirken, örneğin, bir dizi NURBS eğrisi arasında enterpolasyon yapan bir NURBS yüzeyi oluştururken veya bitişik eğrileri birleştirirken sıklıkla kullanılır. Süreçte, farklı eğriler aynı dereceye, genellikle eğri kümesinin maksimum derecesine getirilmelidir. Süreç, derece yükseltme olarak bilinir.
Eğrilik
Diferansiyel geometride en önemli özellik eğriliktir 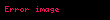
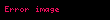

Örnek: bir daire

Rasyonel olmayan eğriler veya Bézier eğrileri bir daireye yaklaşabilir, ancak onu tam olarak temsil edemezler. Rasyonel eğriler, daire dahil herhangi bir konik bölümü tam olarak temsil edebilir. Bu temsil benzersiz değildir, ancak aşağıda bir olasılık görülmektedir:
| x | y | z | Weight |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 |  |
| 0 | 1 | 0 | 1 |
| -1 | 1 | 0 |  |
| -1 | 0 | 0 | 1 |
| -1 | -1 | 0 |  |
| 0 | -1 | 0 | 1 |
| 1 | -1 | 0 |  |
| 1 | 0 | 0 | 1 |
Sıra üçtür, çünkü bir daire ikinci dereceden bir eğridir ve spline'ın sırası, parçalı polinom segmentlerinin derecesinden bir fazladır. Düğüm vektörü 
Eğri tam olarak bir daireyi temsil eder, ancak dairenin yay uzunluğunda tam olarak parametreleştirilmez. Bu, örneğin şu anlama gelir: 




Ayrıca bakınız
- Spline
- Bézier yüzeyi
- de Boor algoritması
- Üçgen örgü
- Nokta bulutu
- Akılcı hareket
- İzogeometrik analiz
Kaynakça
- ^ . MACTECH. 19 Ağustos 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Eylül 2014.
- ^ Schoenberg (19 Ağustos 1964). "Spline Functions and the Problem of Graduation" (PDF). Proceedings of the National Academy of Sciences of the United States of America. National Academy of Sciences. 52 (4): 947-950. doi:10.1073/pnas.52.4.947. (PMC) 300377 $2. (PMID) 16591233. 30 Eylül 2007 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2012.
- ^ Foley, van Dam, Feiner & Hughes: , section 11.2, Addison-Wesley 1996 (2nd ed.
- ^ Bio-Inspired Self-Organizing Robotic Systems. s. 9. Erişim tarihi: 6 Ocak 2014.
- ^ "Rational B-splines". www.cl.cam.ac.uk. 3 Mayıs 2002 tarihinde kaynağından . Erişim tarihi: 20 Eylül 2020.
- ^ . www.cs.mtu.edu. 21 Aralık 2002 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Eylül 2020.
- ^ David F. Rogers: An Introduction to NURBS with Historical Perspective, section 7.1
- ^ The Nature of Mathematical Modeling. Cambridge University Press. 1999. s. 141. ISBN .
- ^ a b c d The NURBS Book. 2. Berlin: Springer. 1997. ISBN .
- ^ Piegl (1989). "Modifying the shape of rational B-splines. Part 1: curves". Computer-Aided Design. 21 (8): 509-518. doi:10.1016/0010-4485(89)90059-6.
- Uzman olmayanlar için NURBS hakkında net açıklama 15 Eylül 2020 tarihinde Wayback Machine sitesinde .
- Etkileşimli NURBS demosu 28 Ocak 2021 tarihinde Wayback Machine sitesinde .
- Düzgün Olmayan Rational B-Splines Hakkında - NURBS 19 Ekim 2016 tarihinde Wayback Machine sitesinde .
- TinySpline: Çeşitli diller için bağlamalar içeren Açık Kaynak C kitaplığı 17 Eylül 2020 tarihinde Wayback Machine sitesinde .
- Inspire kullanarak NURBS Eğrileri ve Yüzeyleri Oluşturun ve Kontrol Edin 28 Eylül 2020 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Duzgun olmayan rasyonel temelli egri Ingilizce Non uniform rational basis spline NURBS egrileri ve yuzeyleri olusturmak ve temsil etmek icin bilgisayar grafiklerinde yaygin olarak kullanilan matematiksel bir modeldir Hem analitik ortak matematiksel formullerle tanimlanan yuzeyler hem de modellenmis sekilleri islemek icin buyuk esneklik ve hassasiyet sunar NURBS yaygin olarak bilgisayar destekli tasarim CAD imalat CAM ve muhendislikte CAE kullanilir ve IGES STEP ACIS ve PHIGS gibi cok sayida endustri capinda standardin parcasidir NURBS araclari ayrica cesitli 3B modelleme ve animasyon yazilim paketlerinde de bulunur NURBS yuzeyleri uc boyutlu uzayda bir yuzeye eslenen iki parametrenin islevleridir Yuzeyin sekli kontrol noktalari ile belirlenir NURBS yuzeyleri kompakt bir bicimde basit geometrik sekilleri temsil edebilir T spline lar ve alt bolme yuzeyleri NURBS yuzeylerine kiyasla kontrol noktalarinin sayisini iki kat azalttigi icin karmasik organik sekiller icin daha uygundur NURBS egrilerini ve yuzeylerini duzenlemek oldukca sezgisel ve ongorulebilirdir Kontrol noktalari her zaman dogrudan egriye yuzeye baglanir veya bir lastik bantla baglanmis gibi davranir Kullanici arayuzunun turune bagli olarak duzenleme Bezier egrileri icin en acik ve yaygin olan bir elemanin kontrol noktalari araciligiyla veya spline modelleme veya hiyerarsik duzenleme gibi daha yuksek seviyeli araclar araciligiyla gerceklestirilebilir Bir NURBS egrisi Ayrica bu animasyonlu surume bakin TarihBir egri Bilgisayarlardan once tasarimlar cesitli cizim araclariyla kagit uzerine elle cizilirdi Cetveller duz cizgiler kullanildi pergel cevreler icin ve protractors acilar icin Ancak bir geminin pruvasinin serbest bicimli egrisi gibi bircok sekil bu aletlerle cizilemezdi Bu tur egriler cekim tahtasinda serbestce cizilebilmesine ragmen gemi yapimcilari genellikle elle yapilamayacak gercek boyutlu bir versiyona ihtiyac duyuyordu Bu tur buyuk cizimler spline adi verilen esnek ahsap seritlerin yardimiyla yapildi Spline lar ordekler adi verilen onceden belirlenmis birkac noktada yerinde tutuldu ordekler arasinda yivli malzemenin esnekligi seridin bukulme enerjisini en aza indiren sekli almasina neden oldu boylece kisitlamalara uyan mumkun olan en puruzsuz sekli olusturdu Ordekler hareket ettirilerek sekil ayarlanabilir 1946 da matematikciler spline seklini incelemeye basladilar ve spline egrisi veya spline fonksiyonu olarak bilinen parcali polinom formulu turettiler IJ Schoenberg teknik ressamlar tarafindan kullanilan mekanik egriye benzerliginden sonra spline islevine adini verdi Bilgisayarlar tasarim surecine dahil edilirken bu tur egrilerin fiziksel ozellikleri matematiksel hassasiyetle modellenebilmeleri ve gerektiginde yeniden uretilebilmeleri icin arastirildi Fransa da Renault muhendisi Pierre Bezier ve Citroen in fizikci ve matematikcisi Paul de Casteljau oncu calismalar yapti Birbirlerine neredeyse paralel calistilar ancak Bezier calismasinin sonuclarini yayinladigi icin Bezier egrilerine onun adi verilirken de Casteljau nun adi yalnizca ilgili algoritmalarla iliskilendirildi Baslangicta NURBS sadece otomobil sirketlerinin tescilli CAD paketlerinde kullaniliyordu Daha sonra standart bilgisayar grafik paketlerinin bir parcasi oldular NURBS egrilerinin ve yuzeylerinin gercek zamanli etkilesimli olarak olusturulmasi ilk olarak 1989 da Silicon Graphics is istasyonlarinda ticari olarak saglandi 1993 yilinda NoRBS adi verilen PC ler icin ilk etkilesimli NURBS modelleyicisi Berlin Teknik Universitesi ile isbirligi yapan kucuk bir baslangic sirketi olan CAS Berlin tarafindan gelistirildi SureklilikYapim asamasinda olan bir yuzey ornegin bir motorlu yatin govdesi genellikle yama olarak bilinen birkac NURBS yuzeyinden olusur Bu yamalar sinirlar gorunmeyecek sekilde birbirine takilmalidir Bu matematiksel olarak geometrik sureklilik kavrami ile ifade edilir NURBS nin farkli seviyelerde geometrik sureklilik olusturma ve kurma becerisinden yararlanan daha yuksek seviyeli araclar mevcuttur Konumsal sureklilik G 0 iki egrinin veya yuzeyin son konumlari cakistigi zaman gecerlidir Egriler veya yuzeyler yine de bir aciyla birleserek keskin bir kose veya kenara yol acabilir ve kirilmis vurgulara neden olabilir Tegetsel sureklilik G egrilerin veya yuzeylerin uc vektorlerinin paralel olmasini ve keskin kenarlari ekarte ederek ayni sekilde isaret etmesini gerektirir Teget olarak surekli bir kenara dusen vurgular her zaman sureklidir ve bu nedenle dogal gorundugunden bu sureklilik duzeyi cogu zaman yeterli olabilir Egrilik surekliligi G ayrica uc vektorlerin ayni uzunlukta ve uzunluk degisim hizinda olmasini gerektirir Surekli egrilikli bir kenara dusen parlak noktalar herhangi bir degisiklik gostermez ve iki yuzeyin tek olarak gorunmesine neden olur Bu gorsel olarak mukemmel derecede puruzsuz olarak taninabilir Bu sureklilik duzeyi tek bir surekli yuzey olusturan bircok iki kubik yama gerektiren modellerin olusturulmasinda cok kullanislidir Geometrik sureklilik esas olarak ortaya cikan yuzeyin seklini ifade eder NURBS yuzeyleri fonksiyonlar oldugundan yuzeyin turevlerini parametrelere gore tartismak da mumkundur Bu parametrik sureklilik olarak bilinir Belirli bir derecenin parametrik surekliligi o derecenin geometrik surekliligini ifade eder Birinci ve ikinci duzey parametrik sureklilik C 0 ve C pratik amaclar icin konumsal ve tegetsel G 0 ve G sureklilikle aynidir Bununla birlikte ucuncu duzey parametrik sureklilik C parametrelendirmesinin de surekli olmasi nedeniyle egrilik surekliliginden farklidir Uygulamada tek tip B spline lar kullanilirsa C surekliligi elde etmek daha kolaydir C n surekliliginin tanimi bitisik egrilerin yuzeylerin n inci turevinin dnC u dun displaystyle d n C u du n bir eklemde esittir Egrilerin ve yuzeylerin kismi turevlerinin bir yonu ve bir buyuklugu olan vektorler olduguna dikkat edin her ikisi de esit olmalidir Parlak noktalar ve yansimalar en azindan G surekliligine sahip NURBS yuzeyleri olmadan elde edilmesi pratik olarak imkansiz olan mukemmel duzlestirmeyi ortaya cikarabilir Bu ayni ilke yuzey degerlendirme yontemlerinden biri olarak kullanilir bu yontemle uzerine yansiyan beyaz seritlere sahip bir yuzeyin isin izlemeli veya yansima haritalanmis bir goruntusu bir yuzey veya bir dizi yuzey uzerindeki en kucuk sapmalari bile gosterecektir Bu yontem araba yuzeyindeki neon isikli tavanin yansimalarinin kalitesinin kontrol edilmesiyle yuzey kalitesinin denetlendigi otomobil prototiplemesinden turetilmistir Bu yontem ayni zamanda Zebra analizi olarak da bilinir Teknik ozelliklerBir NURBS egrisi sirasi bir dizi agirlikli kontrol noktasi ve bir dugum vektoru ile tanimlanir NURBS egrileri ve yuzeyleri hem B spline larin hem de Bezier egrilerinin ve yuzeylerinin genellestirmeleridir birincil fark NURBS egrilerini rasyonel kilan kontrol noktalarinin agirliklandirilmasidir Sigara rasyonel bir deyisle basit B spline her kontrol noktasi normal homojen olmayan yerine daha w no koordinat oransal B spline ozel bir durum alt kume vardir homojen koordinat Bu her kontrol noktasinda 1 agirliga sahip olmaya esdegerdir Rasyonel B spline bir agirlik olarak her bir kontrol noktasinin w kullanin Iki boyutlu kontrol noktalari izgarasi kullanilarak duzlemsel yamalar ve kurelerin bolumleri dahil NURBS yuzeyleri olusturulabilir Bunlar iki degiskenle parametrelendirilir tipik olarak s ve t veya u ve v olarak adlandirilir Bu NURBS haritalamasi olusturmak icin rastgele boyutlara genisletilebilir Rn Rn displaystyle mathbb R n to mathbb R n NURBS egrileri ve yuzeyleri birkac nedenden dolayi kullanislidir Belirli bir sira icin NURBS kumesi afin donusumler altinda degismez dondurme ve oteleme gibi islemler NURBS egrilerine ve yuzeylerine kontrol noktalarina uygulanarak uygulanabilir Hem standart analitik sekiller or Konikler hem de serbest bicimli sekiller icin ortak bir matematiksel form sunarlar Cok cesitli sekiller tasarlama esnekligi saglarlar Sekilleri depolarken bellek tuketimini azaltirlar daha basit yontemlere kiyasla Sayisal olarak kararli ve dogru algoritmalarla oldukca hizli bir sekilde degerlendirilebilirler Sonraki bolumlerde NURBS tek boyutta egriler tartisilmaktadir Hepsi iki veya daha fazla boyuta genellenebilir NURBS egrisinin kuvveti Bir NURBS egrisinin kuvveti egri uzerindeki herhangi bir noktayi etkileyen yakin kontrol noktalarinin sayisini tanimlar Egri matematiksel olarak egrinin mertebesinden bir dereceden daha dusuk bir polinom ile temsil edilir Bu nedenle ikinci dereceden egrilere dogrusal polinomlarla temsil edilenler dogrusal egriler ucuncu dereceden egrilere ikinci dereceden egriler ve dorduncu dereceden egrilere kubik egriler denir Kontrol noktalarinin sayisi egrinin kuvvetinden buyuk veya ona esit olmalidir Pratikte kubik egriler en sik kullanilanlardir Besinci ve altinci mertebeden egriler bazen ozellikle surekli yuksek mertebeden turevler elde etmek icin kullanislidir ancak daha yuksek mertebeden egriler pratikte hicbir zaman kullanilmaz cunku bunlar dahili sayisal problemlere yol acar ve orantisiz sekilde buyuk hesaplama sureleri gerektirme egilimindedirler Kontrol noktalari Uc boyutlu NURBS yuzeyleri karmasik organik sekillere sahip olabilir Kontrol noktalari yuzeyin aldigi yonleri etkiler Asagidaki en distaki kare yuzeyin X Y kapsamini gosterir Kontrol noktalari egrinin seklini belirler Tipik olarak egrinin her noktasi bir dizi kontrol noktasinin agirlikli toplami alinarak hesaplanir Her bir noktanin agirligi gecerli parametreye gore degisir D derecelik bir egri icin herhangi bir kontrol noktasinin agirligi parametre uzayinin d 1 araliklarinda yalnizca sifirdan farklidir Bu araliklar icinde agirlik d derecesinin bir polinom fonksiyonuna temel fonksiyonlar gore degisir Araliklarin sinirlarinda temel fonksiyonlar sorunsuz bir sekilde sifira gider puruzsuzluk polinomun derecesine gore belirlenir Ornek olarak birinci derecenin temel islevi bir ucgen islevidir Sifirdan bire yukselir sonra tekrar sifira duser Yukselirken onceki kontrol noktasinin temel islevi duser Bu sekilde egri iki nokta arasinda interpolasyon yapar ve ortaya cikan egri aralikli sinirlarda veya dugumlerde turevlenemeyen surekli olan bir cokgendir Daha yuksek dereceli polinomlar buna bagli olarak daha surekli turevlere sahiptir Aralik icinde temel fonksiyonlarin polinom dogasinin ve yapinin dogrusalliginin egriyi mukemmel bir sekilde puruzsuz hale getirdigine dikkat edin bu nedenle sureksizlik sadece dugumlerde ortaya cikabilir Pek cok uygulamada tek bir kontrol noktasinin yalnizca aktif oldugu araliklari etkilemesi yerel destek olarak bilinen oldukca istenen bir ozelliktir Modellemede bir yuzeyin bir kisminin degistirilmesine izin verirken diger kisimlarin degismeden kalmasina izin verir Daha fazla kontrol noktasi eklemek belirli bir egriye daha iyi yaklasima izin verir ancak yalnizca belirli bir egri sinifi tam olarak sinirli sayida kontrol noktasiyla temsil edilebilir NURBS egrileri ayrica her kontrol noktasi icin bir skaler agirlik icerir Bu kontrol noktalarinin sayisini gereksiz yere yukseltmeden egrinin sekli uzerinde daha fazla kontrole izin verir Ozellikle tam olarak temsil edilebilen egriler kumesine daire ve elips gibi konik bolumler ekler NURBS deki rasyonel terimi bu agirliklari ifade eder Kontrol noktalari herhangi bir boyutluluga sahip olabilir Tek boyutlu noktalar sadece parametrenin skaler bir fonksiyonunu tanimlar Bunlar genellikle parlakligi ve renk egrilerini ayarlamak icin goruntu isleme programlarinda kullanilir Uc boyutlu kontrol noktalari 3B uzayda bir konum olan nokta kelimesinin gunluk anlaminda kullanildigi 3B modellemede bolca kullanilir Cok boyutlu noktalar bir robot kolunun farkli konumsal ve donme ayarlari gibi zamana bagli deger kumelerini kontrol etmek icin kullanilabilir NURBS yuzeyleri bunun sadece bir uygulamasidir Her kontrol noktasi aslinda bir egri tanimlayan tam bir kontrol noktalari vektorudur Bu egriler derecelerini ve kontrol noktalarinin sayisini paylasir ve parametre uzayinin bir boyutunu kapsar Bu kontrol vektorlerinin parametre uzayinin diger boyutu uzerinde enterpolasyonuyla yuzeyi tanimlayan surekli bir egri seti elde edilir Dugum vektor Dugum vektoru kontrol noktalarinin NURBS egrisini nerede ve nasil etkiledigini belirleyen bir parametre degerleri dizisidir Dugum sayisi her zaman kontrol noktalarinin sayisi arti egri derecesi arti birdir yani kontrol noktalarinin sayisi arti egri sirasi Dugum vektoru parametrik alani daha once bahsedilen araliklarla boler genellikle dugum araliklari olarak anilir Parametre degeri yeni bir dugum araligina her girdiginde yeni bir kontrol noktasi aktif hale gelirken eski bir kontrol noktasi atilir Dugum vektorundeki degerlerin azalan sirada olmasi gerektigi dolayisiyla 0 0 1 2 3 3 gecerliyken 0 0 2 1 3 3 gecerli degildir Ardisik dugumler ayni degere sahip olabilir Bu daha sonra sifir uzunlukta bir dugum araligini tanimlar bu da iki kontrol noktasinin ayni anda etkinlestirildigini ve tabii ki iki kontrol noktasinin devre disi birakildigini gosterir Bunun ortaya cikan egrinin veya daha yuksek turevlerinin surekliligi uzerinde etkisi vardir ornegin baska turlu puruzsuz bir NURBS egrisinde koselerin olusturulmasina izin verir Cakisan dugum bir dizi bazen belirli bir cogu ile bir dugum olarak adlandirilir Coklugu iki veya uc olan dugumler cift veya uclu dugum olarak bilinir Bir dugumun coklugu egrinin derecesiyle sinirlidir cunku daha yuksek bir cokluk egriyi ayrik parcalara boler ve kontrol noktalarini kullanilmadan birakir Birinci derece NURBS icin her dugum bir kontrol noktasi ile eslestirilir Dugum vektoru genellikle siraya esit cokluga sahip bir dugumle baslar Bu mantiklidir cunku bu ilk dugum araligi uzerinde etkisi olan kontrol noktalarini etkinlestirir Benzer sekilde dugum vektoru genellikle bu coklugun bir dugumu ile biter Bu tur dugum vektorlerine sahip egriler bir kontrol noktasinda baslar ve biter Dugumlerin degerleri giris parametresi ile karsilik gelen NURBS degeri arasindaki eslesmeyi kontrol eder Ornegin bir NURBS zaman icinde uzayda bir yolu tanimliyorsa dugumler islevin kontrol noktalarindan sonra ilerledigi zamani kontrol eder Bununla birlikte sekilleri temsil etme amaclari icin yalnizca dugum degerleri arasindaki farkin oranlari onemlidir bu durumda dugum vektorleri 0 0 1 2 3 3 ve 0 0 2 4 6 6 ayni egriyi uretir Dugum degerlerinin pozisyonlari parametre uzayinin egri uzayiyla eslestirilmesini etkiler Bir NURBS egrisinin olusturulmasi genellikle parametre araliginda sabit bir adimla adimlanarak yapilir Dugum araligi uzunluklari degistirilerek egriligin yuksek oldugu bolgelerde daha fazla numune noktasi kullanilabilir Diger bir kullanim parametre degerinin bir miktar fiziksel oneme sahip oldugu durumlarda ornegin parametre zaman ise ve egri bir robot kolunun hareketini tanimliyorsa Dugum araligi uzunluklari daha sonra robot koluna veya cevresine zarar gelmesini onlemek icin dogru olmak icin gerekli olan hiz ve ivmeye donusur Haritalamadaki bu esneklik NURBS deki tek tip olmayan ifadesinin kastettigi seydir Yalnizca dahili hesaplamalar icin gerekli olan dugumler genellikle modelleme yazilimi kullanicilari icin yararli degildir Bu nedenle bircok modelleme uygulamasi dugumleri duzenlenebilir ve hatta gorunur hale getirmez Kontrol noktalarindaki varyasyona bakarak makul dugum vektorleri olusturmak genellikle mumkundur NURBS yaziliminin daha yeni surumleri ornegin Autodesk Maya ve Rhinoceros 3D dugum konumlarinin etkilesimli olarak duzenlenmesine izin verir ancak bu kontrol noktalarinin duzenlenmesinden onemli olcude daha az sezgiseldir Temel fonksiyonlarin olusturulmasi NURBS egrilerinin olusturulmasinda kullanilan B spline temel fonksiyonlari genellikle su sekilde belirtilir Ni n u displaystyle N i n u icinde i displaystyle i karsilik gelir i displaystyle i inci kontrol noktasi ve n displaystyle n temel islevin derecesine karsilik gelir Parametre bagimliligi genellikle disarida birakilir boylece yazabiliriz Ni n displaystyle N i n Bu temel islevlerin tanimi n displaystyle n Derece 0 fonksiyonlari Ni 0 displaystyle N i 0 parcali sabit fonksiyonlardir Karsilik gelen dugum araliginda bir ve diger her yerde sifirdir Etkili bir sekilde Ni n displaystyle N i n dogrusal bir enterpolasyondur Ni n 1 displaystyle N i n 1 ve Ni 1 n 1 displaystyle N i 1 n 1 Son iki islev sifirdan farklidir n displaystyle n dugum araliklari ortusen n 1 displaystyle n 1 dugum acikliklari Islev Ni n displaystyle N i n olarak hesaplanir Yukaridan asagiya Dogrusal temel fonksiyonlar N1 1 displaystyle N 1 1 mavi ve N2 1 displaystyle N 2 1 yesil ustte agirlik fonksiyonlari f displaystyle f ve g displaystyle g orta ve ortaya cikan ikinci dereceden temel islevi alt Dugumler 0 1 2 ve 2 5Ni n fi nNi n 1 gi 1 nNi 1 n 1 displaystyle N i n f i n N i n 1 g i 1 n N i 1 n 1 fi displaystyle f i sifirdan bire dogrusal olarak yukselir burada aralikta Ni n 1 displaystyle N i n 1 sifir olmayan gi 1 displaystyle g i 1 aralikta birden sifira duser burada Ni 1 n 1 displaystyle N i 1 n 1 sifir degildir Onceden belirtildigi uzere Ni 1 displaystyle N i 1 iki dugum boyunca sifirdan farkli bir fonksiyondur ilkinde sifirdan bire yukselen ve ikinci dugum araliginda sifira dusen Daha yuksek dereceli temel fonksiyonlar karsilik gelen daha fazla dugum araligi uzerinde sifirdan farklidir ve buna gore daha yuksek dereceye sahiptir Eger u displaystyle u parametredir ve ki displaystyle k i i displaystyle i inci dugum fonksiyonlari yazabiliriz f displaystyle f ve g displaystyle g gibi fi n u u kiki n ki displaystyle f i n u u k i over k i n k i ve gi n u 1 fi n u ki n uki n ki displaystyle g i n u 1 f i n u k i n u over k i n k i Fonksiyonlar f displaystyle f ve g displaystyle g karsilik gelen alt sira temel islevleri sifir olmadiginda pozitiftir N deki tumevarim yoluyla temel fonksiyonlarin tum degerleri icin negatif olmadigini izler n displaystyle n ve u displaystyle u Bu temel fonksiyonlarin hesaplanmasini sayisal olarak kararli hale getirir Yine tumevarimla parametrenin belirli bir degeri icin temel fonksiyonlarin toplaminin birlik oldugu kanitlanabilir Bu temel islevlerin birlik ozelliginin bolumu olarak bilinir Sekiller 0 1 2 3 4 4 1 5 1 6 1 7 1 dugumler icin dogrusal ve ikinci dereceden temel fonksiyonlari gosterir Bir dugum araligi digerlerinden oldukca kisadir Bu dugum araliginda ikinci dereceden temel fonksiyonundaki tepe daha belirgindir ve neredeyse bire ulasir Tersine bitisik temel islevler daha hizli sifira duser Geometrik yorumlamada bu egrinin karsilik gelen kontrol noktasina yakindan yaklastigi anlamina gelir Cift dugum durumunda dugum acikliginin uzunlugu sifir olur ve tepe tam olarak bire ulasir Temel islev artik bu noktada farklilastirilamaz Komsu kontrol noktalari esdogrusal degilse egri keskin bir koseye sahip olacaktir NURBS egrisinin genel formu Temel fonksiyonlarin tanimlarini kullanma Ni n displaystyle N i n onceki paragraftan bir NURBS egrisi asagidaki bicimi alir C u i 1kNi nwi j 1kNj nwjPi i 1kNi nwiPi i 1kNi nwi displaystyle C u sum i 1 k frac N i n w i sum j 1 k N j n w j mathbf P i frac sum i 1 k N i n w i mathbf P i sum i 1 k N i n w i Bunda k displaystyle k kontrol noktalarinin sayisi Pi displaystyle mathbf P i ve wi displaystyle w i karsilik gelen agirliklardir Payda tum agirliklarin bir olup olmadigini degerlendiren normallestirme faktorudur Bu temel islevlerin birlik ozelliginin bolumlemesinden gorulebilir Bunu su sekilde yazmak gelenekseldir C u i 1kRi n u Pi displaystyle C u sum i 1 k R i n u mathbf P i Ri n u Ni n u wi j 1kNj n u wj displaystyle R i n u N i n u w i over sum j 1 k N j n u w j rasyonel temel islevler olarak bilinir NURBS yuzeyinin genel formu Iki NURBS egrisinin tensor urunu olarak bir NURBS yuzeyi elde edilir boylece iki bagimsiz parametre kullanilir u displaystyle u ve v displaystyle v endekslerle i displaystyle i ve j displaystyle j sirasiyla S u v i 1k j 1lRi j u v Pi j displaystyle S u v sum i 1 k sum j 1 l R i j u v mathbf P i j ile Ri j u v Ni n u Nj m v wi j p 1k q 1lNp n u Nq m v wp q displaystyle R i j u v frac N i n u N j m v w i j sum p 1 k sum q 1 l N p n u N q m v w p q rasyonel temel islevler olarak NURBS nesnelerini duzenlemeMotoryat tasarimi Bir NURBS nesnesine bir dizi donusum uygulanabilir Ornegin bazi egri belirli bir derece ve N kontrol noktasi kullanilarak tanimlanirsa ayni egri ayni derece ve N 1 kontrol noktalari kullanilarak ifade edilebilir Islemde bir dizi kontrol noktasi pozisyon degistirir ve dugum vektorune bir dugum eklenir Bu manipulasyonlar etkilesimli tasarim sirasinda yogun bir sekilde kullanilir Bir kontrol noktasi eklerken egrinin sekli ayni kalmali ve sonraki ayarlamalar icin baslangic noktasi olusturmalidir Bu islemlerden birkaci asagida tartisilmaktadir Dugum ekleme Terimden de anlasilacagi gibi dugum ekleme dugum vektorune bir dugum ekler Egrinin derecesi ise n displaystyle n sonra n 1 displaystyle n 1 kontrol noktalari ile degistirilir n displaystyle n Yeni olanlar Egrinin sekli ayni kalir Bir dugum dugumun maksimum cokluguna kadar birden cok kez eklenebilir Bu bazen dugum iyilestirme olarak adlandirilir ve tekrarlanan dugum eklemeden daha verimli olan bir algoritma ile elde edilebilir Dugum cikarma Dugum cikarma dugum atmanin tersidir Amaci daha kompakt bir gorunum elde etmek icin dugumleri ve ilgili kontrol noktalarini kaldirmaktir Aciktir ki egrinin tam seklini korurken bu her zaman mumkun degildir Pratikte bir dugumun kaldirilip kaldirilamayacagini belirlemek icin dogrulukta bir tolerans kullanilir Islem kontrol noktalarinin manuel olarak eklenmis olabilecegi etkilesimli bir oturumdan sonra veya basit bir donusturme isleminin gereksiz kontrol noktalarina yol actigi farkli bir temsilden bir egri ice aktarildiktan sonra temizlemek icin kullanilir Derece yukselmesi Belirli bir derecedeki bir NURBS egrisi her zaman daha yuksek dereceli bir NURBS egrisi ile temsil edilebilir Bu ayri NURBS egrilerini birlestirirken ornegin bir dizi NURBS egrisi arasinda enterpolasyon yapan bir NURBS yuzeyi olustururken veya bitisik egrileri birlestirirken siklikla kullanilir Surecte farkli egriler ayni dereceye genellikle egri kumesinin maksimum derecesine getirilmelidir Surec derece yukseltme olarak bilinir Egrilik Diferansiyel geometride en onemli ozellik egriliktir k displaystyle kappa Yerel ozellikleri kenarlar koseler vb Ve birinci ve ikinci turev arasindaki iliskileri ve dolayisiyla kesin egri seklini aciklar Turevleri belirledikten sonra hesaplamasi kolaydir k r t r t r t 3 displaystyle kappa frac r t times r t r t 3 veya ikinci turevden yay uzunlugu olarak yaklastirilir k r so displaystyle kappa r s o Egriligin dogrudan hesaplanmasi k displaystyle kappa bu denklemlerle parametrelestirilmis egrilerin poligonal gosterimlerine karsi buyuk avantaji vardir Ornek bir daireNURBS daireleri tam olarak tanimlama yetenegine sahiptir Burada siyah ucgen bir NURBS egrisinin kontrol cokgenidir w 1 de gosterilmistir Mavi noktali cizgi bir B spline egrisinin karsilik gelen kontrol poligonunu NURBS yi kontrol noktalari ile karsilik gelen agirliklarla carparak olusturulan 3D homojen koordinatlarda gosterir Mavi paraboller uc parabolden olusan 3D deki karsilik gelen B spline egrisidir Nurbs kontrol noktalari ve agirliklar secerek parabol boylece yaylarin 1 w duzlem sonuclari uzerine parabolas proje agirlik bolunmesi 3D orijinde ucu ile gri bir koni karsi yuzeyine paraleldir kirmizi daire bkz konik bolum Rasyonel olmayan egriler veya Bezier egrileri bir daireye yaklasabilir ancak onu tam olarak temsil edemezler Rasyonel egriler daire dahil herhangi bir konik bolumu tam olarak temsil edebilir Bu temsil benzersiz degildir ancak asagida bir olasilik gorulmektedir x y z Weight1 0 0 11 1 0 22 displaystyle scriptstyle frac sqrt 2 2 0 1 0 1 1 1 0 22 displaystyle scriptstyle frac sqrt 2 2 1 0 0 1 1 1 0 22 displaystyle scriptstyle frac sqrt 2 2 0 1 0 11 1 0 22 displaystyle scriptstyle frac sqrt 2 2 1 0 0 1 Sira uctur cunku bir daire ikinci dereceden bir egridir ve spline in sirasi parcali polinom segmentlerinin derecesinden bir fazladir Dugum vektoru 0 0 0 p 2 p 2 p p 3p 2 3p 2 2p 2p 2p displaystyle 0 0 0 pi 2 pi 2 pi pi 3 pi 2 3 pi 2 2 pi 2 pi 2 pi Daire cift dugumlerle birbirine baglanmis dort ceyrek daireden olusur Ucuncu dereceden bir NURBS egrisindeki cift dugum normal olarak birinci turevde sureklilik kaybina yol acsa da kontrol noktalari birinci turevin surekli olacagi sekilde konumlandirilir Aslinda egri her yerde sonsuz derecede turevlenebilir cunku tam olarak bir daireyi temsil ediyor olmasi gerekir Egri tam olarak bir daireyi temsil eder ancak dairenin yay uzunlugunda tam olarak parametrelestirilmez Bu ornegin su anlama gelir t displaystyle t yalan soylemez sin t cos t displaystyle sin t cos t temsil simetrik oldugundan her ceyrek dairenin baslangic orta ve bitis noktalari haric Cemberin x koordinati icin tam bir rasyonel polinom ifadesi saglayacagindan bu imkansiz olurdu cos t displaystyle cos t imkansizdir Daire parametresi olarak bir tam devir yapar t displaystyle t 0 dan 2p displaystyle 2 pi ancak bunun tek nedeni dugum vektorunun keyfi olarak degerin katlari olarak secilmesidir p 2 displaystyle pi 2 Ayrica bakinizSpline Bezier yuzeyi de Boor algoritmasi Ucgen orgu Nokta bulutu Akilci hareket Izogeometrik analizKaynakca MACTECH 19 Agustos 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 26 Eylul 2014 Schoenberg 19 Agustos 1964 Spline Functions and the Problem of Graduation PDF Proceedings of the National Academy of Sciences of the United States of America National Academy of Sciences 52 4 947 950 doi 10 1073 pnas 52 4 947 PMC 300377 2 PMID 16591233 30 Eylul 2007 tarihinde kaynagindan Erisim tarihi 24 Subat 2012 Foley van Dam Feiner amp Hughes section 11 2 Addison Wesley 1996 2nd ed Bio Inspired Self Organizing Robotic Systems s 9 Erisim tarihi 6 Ocak 2014 Rational B splines www cl cam ac uk 3 Mayis 2002 tarihinde kaynagindan Erisim tarihi 20 Eylul 2020 www cs mtu edu 21 Aralik 2002 tarihinde kaynagindan arsivlendi Erisim tarihi 20 Eylul 2020 David F Rogers An Introduction to NURBS with Historical Perspective section 7 1 The Nature of Mathematical Modeling Cambridge University Press 1999 s 141 ISBN 0 521 57095 6 a b c d The NURBS Book 2 Berlin Springer 1997 ISBN 3 540 61545 8 Piegl 1989 Modifying the shape of rational B splines Part 1 curves Computer Aided Design 21 8 509 518 doi 10 1016 0010 4485 89 90059 6 Uzman olmayanlar icin NURBS hakkinda net aciklama 15 Eylul 2020 tarihinde Wayback Machine sitesinde Etkilesimli NURBS demosu 28 Ocak 2021 tarihinde Wayback Machine sitesinde Duzgun Olmayan Rational B Splines Hakkinda NURBS 19 Ekim 2016 tarihinde Wayback Machine sitesinde TinySpline Cesitli diller icin baglamalar iceren Acik Kaynak C kitapligi 17 Eylul 2020 tarihinde Wayback Machine sitesinde Inspire kullanarak NURBS Egrileri ve Yuzeyleri Olusturun ve Kontrol Edin 28 Eylul 2020 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans