Akışkanlar dinamiği alanında, basınç katsayısı bir boyutsuz sayı olup, bir akış alanındaki bağıl basınçları ifade eder. Basınç katsayısı, aerodinamik ve hidrodinamik çalışmalarında kullanılmaktadır. Her bir akış alanında, her konumsal noktanın kendine özgü bir basınç katsayısı, Cp değeri bulunmaktadır.
Aerodinamik ve hidrodinamik alanlarında, birçok durumda, bir cismin yakınındaki bir noktadaki basınç katsayısı, cismin boyutundan bağımsız olarak değerlendirilir. Bu sebeple, bir mühendislik modeli rüzgar tüneli veya test edilerek, modelin çevresindeki kritik noktalardaki basınç katsayıları belirlenebilir ve bu katsayılar, tam boyutlu bir uçak veya geminin etrafındaki kritik noktalardaki akışkan basıncını güvenle tahmin etmek için kullanılabilir.
Tanım
Basınç katsayısı, sıkıştırılamaz ve sıkıştırılabilir akışkanları (su ve hava gibi) incelemek için kullanılan bir parametredir. Boyutsuz katsayı ile boyutlu sayılar arasındaki ilişki şu şekildedir:
burada:
basınç katsayısının hesaplandığı noktadaki (statik basınçtır)
(yani herhangi bir bozulmadan uzak olan, İng. freestream) statik basınçtır
serbest akım akışkan yoğunluğudur (Deniz seviyesinde ve 15 °C'deki hava yoğunluğu 1.225
’tür)
akışkanın serbest akım hızı veya akışkan içerisindeki cismin hızıdır
Sıkıştırılamaz akış
Bernoulli denklemi kullanılarak, basınç katsayısı (viskoz olmayan ve kararlı akışlar) için daha basit hale getirilebilir:
burada:
basınç katsayısının değerlendirildiği noktadaki akış hızıdır
Mach sayısı olup sıfır limitinde değerlendirilir
akışın
Bu ilişki, hız ve basınçtaki değişimlerin, akışkan yoğunluğundaki değişimlerin ihmal edilebileceği kadar küçük olduğu sıkıştırılamaz akışkanların akışı için geçerlidir. Bu varsayım, Mach sayısı yaklaşık olarak 0.3'ün altında olduğunda mühendislik uygulamalarında yaygın olarak kabul edilir.
değerinin sıfır olması, basıncın serbest akım basıncı ile aynı olduğunu belirtir.
değerinin bir olması, karşılık gelir ve bir durgunluk noktasını ifade eder.
- Bir sıvı akışında en negatif
değerleri, kavitasyon sayısına eklenerek kavitasyon marjını verir. Bu marj pozitifse, akış yerel olarak tamamen sıvıdır; sıfır veya negatifse, akış kavitasyon yapmakta veya gaz halindedir.

Bir cismin etrafındaki sıkıştırılamaz akışkan akış alanında, 'bir'e kadar pozitif basınç katsayısına sahip noktalar ve negatif basınç katsayıları (eksi birin altında olan katsayılar dahil) bulunmaktadır.
Sıkıştırılabilir akış
Hava gibi sıkıştırılabilir akışkanların akışında ve özellikle yüksek hızlı sıkıştırılabilir akışkan akışında, 
Perturbasyon teorisi
Basınç katsayısı 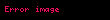



Bernoulli denklemi kullanılarak,
bu denklem şu şekilde yeniden yazılabilir
burada 
Basınç katsayısı şu şekilde ifade edilir:
burada 
Yerel piston teorisi
Klasik piston teorisi, güçlü bir aerodinamik analiz aracıdır. Momentum denklemi ve izentropik perturbasyonların varsayımı kullanılarak, yüzey basıncı için aşağıdaki temel piston teorisi formülü elde edilir:
burada 

Yüzey şu şekilde tanımlanır:
Kayma hızı sınır koşulu (İng. slip velocity boundary condition) şuna yol açar:
Aşağı inhiraf hızı (İng. downwash speed) 
Basınç dağılımı
Belirli bir hücum açısındaki bir kanat profili, basınç dağılımı olarak adlandırılan bir duruma sahiptir. Bu basınç dağılımı, kanat profilinin etrafındaki tüm noktalardaki basınç değerlerini ifade eder. Genellikle, bu dağılımların grafiklerinde negatif değerler grafikte daha yüksek konumda çizilir, çünkü kanat profilinin üst yüzeyindeki 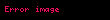
Aerodinamik katsayılarla ilişki
Üç aerodinamik katsayının tamamı, basınç katsayısı eğrisinin kord boyunca integralidir. Kaldırma katsayısı, tamamen yatay yüzeylere sahip iki boyutlu bir kanat profili kesiti için, basınç katsayısı dağılımından entegrasyon yoluyla veya dağılımdaki çizgiler arasındaki alanın hesaplanması ile belirlenebilir. Bu ifade, kaldırma yaklaştırmasının panel yöntemi kullanılarak doğrudan sayısal entegrasyon için uygun değildir, çünkü basınç kaynaklı kaldırma yönünü dikkate almaz. Bu denklem yalnızca sıfır hücum açısı için geçerlidir.
burada:
alt yüzeydeki basınç katsayısıdır
üst yüzeydeki basınç katsayısıdır
ön kenarın konumudur
arka kenarın konumudur
Alt yüzeydeki 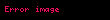
Ayrıca bakınız
Kaynakça
- ^ (1975) Aerodynamics, § 3.6, Pitman Publishing Limited, London.
- ^ Abbott and Von Doenhoff, Theory of Wing Sections, equation 2.24
- ^ Anderson, John D. Fundamentals of Aerodynamics. 4th ed. New York: McGraw Hill, 2007. 219.
- ^ https://thesis.library.caltech.edu/608/1/Scherer_lr_1950.pdf
Diğer okumalar
- Abbott, I.H. and Von Doenhoff, A.E. (1959) Theory of Wing Sections, Dover Publications, Inc. New York, Standard Book No. 486-60586-8
- Anderson, John D (2001) Fundamentals of Aerodynamic 3rd Edition, McGraw-Hill.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Akiskanlar dinamigi alaninda basinc katsayisi bir boyutsuz sayi olup bir akis alanindaki bagil basinclari ifade eder Basinc katsayisi aerodinamik ve hidrodinamik calismalarinda kullanilmaktadir Her bir akis alaninda her konumsal noktanin kendine ozgu bir basinc katsayisi Cp degeri bulunmaktadir Aerodinamik ve hidrodinamik alanlarinda bircok durumda bir cismin yakinindaki bir noktadaki basinc katsayisi cismin boyutundan bagimsiz olarak degerlendirilir Bu sebeple bir muhendislik modeli ruzgar tuneli veya test edilerek modelin cevresindeki kritik noktalardaki basinc katsayilari belirlenebilir ve bu katsayilar tam boyutlu bir ucak veya geminin etrafindaki kritik noktalardaki akiskan basincini guvenle tahmin etmek icin kullanilabilir TanimBasinc katsayisi sikistirilamaz ve sikistirilabilir akiskanlari su ve hava gibi incelemek icin kullanilan bir parametredir Boyutsuz katsayi ile boyutlu sayilar arasindaki iliski su sekildedir Cp p p 12r V 2 displaystyle C p p p infty over frac 1 2 rho infty V infty 2 burada p displaystyle p basinc katsayisinin hesaplandigi noktadaki statik basinctir p displaystyle p infty yani herhangi bir bozulmadan uzak olan Ing freestream statik basinctir r displaystyle rho infty serbest akim akiskan yogunlugudur Deniz seviyesinde ve 15 C deki hava yogunlugu 1 225 kg m3 displaystyle rm kg m 3 tur V displaystyle V infty akiskanin serbest akim hizi veya akiskan icerisindeki cismin hizidirSikistirilamaz akisBernoulli denklemi kullanilarak basinc katsayisi viskoz olmayan ve kararli akislar icin daha basit hale getirilebilir Cp M 0 p p p0 p 1 uu 2 displaystyle C p M approx 0 p p infty over p 0 p infty 1 bigg frac u u infty bigg 2 burada u displaystyle u basinc katsayisinin degerlendirildigi noktadaki akis hizidir M displaystyle M Mach sayisi olup sifir limitinde degerlendirilir p0 displaystyle p 0 akisin Bu iliski hiz ve basinctaki degisimlerin akiskan yogunlugundaki degisimlerin ihmal edilebilecegi kadar kucuk oldugu sikistirilamaz akiskanlarin akisi icin gecerlidir Bu varsayim Mach sayisi yaklasik olarak 0 3 un altinda oldugunda muhendislik uygulamalarinda yaygin olarak kabul edilir Cp displaystyle C p degerinin sifir olmasi basincin serbest akim basinci ile ayni oldugunu belirtir Cp displaystyle C p degerinin bir olmasi karsilik gelir ve bir durgunluk noktasini ifade eder Bir sivi akisinda en negatif Cp displaystyle C p degerleri kavitasyon sayisina eklenerek kavitasyon marjini verir Bu marj pozitifse akis yerel olarak tamamen sividir sifir veya negatifse akis kavitasyon yapmakta veya gaz halindedir Cp 1 displaystyle C p 1 olan noktalar planor tasariminda onem tasir cunku bu varyometreye sinyal basinci saglamak icin uygun bir toplam enerji portu yerini gosterir Varyometre atmosferin dikey hareketlerine tepki verir ancak planorun dikey manevralarina tepki vermez Bir cismin etrafindaki sikistirilamaz akiskan akis alaninda bir e kadar pozitif basinc katsayisina sahip noktalar ve negatif basinc katsayilari eksi birin altinda olan katsayilar dahil bulunmaktadir Sikistirilabilir akisHava gibi sikistirilabilir akiskanlarin akisinda ve ozellikle yuksek hizli sikistirilabilir akiskan akisinda 12rv2 displaystyle frac 1 2 rho v 2 artik ile statik basinc arasindaki farkin dogru bir olcusu olarak kabul edilmez Ayrica toplam basinca esit oldugu tanidik iliski her zaman gecerli degildir Bu izentropik akista her zaman dogrudur ancak sok dalgasinin varligi akisin izotermal olmasindan sapmasina neden olabilir Sonuc olarak sikistirilabilir akista basinc katsayilari birden buyuk olabilir Perturbasyon teorisi Basinc katsayisi Cp displaystyle C p Ing irrotational flow ve izentropik akis icin serbest akim hizi u displaystyle u infty ile normalize edilen potansiyel F displaystyle Phi ve perturbasyon potansiyeli ϕ displaystyle phi tanitilarak tahmin edilebilir F u x ϕ x y z displaystyle Phi u infty x phi x y z Bernoulli denklemi kullanilarak F t F F2 gg 1pr sabit displaystyle frac partial Phi partial t frac nabla Phi cdot nabla Phi 2 frac gamma gamma 1 frac p rho text sabit bu denklem su sekilde yeniden yazilabilir F t F F2 a2g 1 sabit displaystyle frac partial Phi partial t frac nabla Phi cdot nabla Phi 2 frac a 2 gamma 1 text sabit burada a displaystyle a ses hizidir Basinc katsayisi su sekilde ifade edilir Cp p p g2p M2 2gM2 aa 2gg 1 1 2gM2 g 1a 2 u 22 Ft F F2 1 gg 1 1 2gM2 1 g 1a 2 ϕt u ϕx gg 1 1 2ϕtu 2 2ϕxu displaystyle begin aligned C p amp frac p p infty frac gamma 2 p infty M 2 frac 2 gamma M 2 left left frac a a infty right frac 2 gamma gamma 1 1 right amp frac 2 gamma M 2 left left frac gamma 1 a infty 2 frac u infty 2 2 Phi t frac nabla Phi cdot nabla Phi 2 1 right frac gamma gamma 1 1 right amp approx frac 2 gamma M 2 left left 1 frac gamma 1 a infty 2 phi t u infty phi x right frac gamma gamma 1 1 right amp approx frac 2 phi t u infty 2 frac 2 phi x u infty end aligned burada a displaystyle a infty uzak alan ses hizidir Yerel piston teorisi Klasik piston teorisi guclu bir aerodinamik analiz aracidir Momentum denklemi ve izentropik perturbasyonlarin varsayimi kullanilarak yuzey basinci icin asagidaki temel piston teorisi formulu elde edilir p p 1 g 12wa 2gg 1 displaystyle p p infty left 1 frac gamma 1 2 frac w a right frac 2 gamma gamma 1 burada w displaystyle w asagi inhiraf hizi Ing downwash speed ve a displaystyle a ses hizidir Cp p p g2p M2 2gM2 1 g 12wa 2gg 1 1 displaystyle C p frac p p infty frac gamma 2 p infty M 2 frac 2 gamma M 2 left left 1 frac gamma 1 2 frac w a right frac 2 gamma gamma 1 1 right Yuzey su sekilde tanimlanir F x y z t z f x y t 0 displaystyle F x y z t z f x y t 0 Kayma hizi sinir kosulu Ing slip velocity boundary condition suna yol acar F F u ϕx ϕy ϕz Vduvar F F F t1 F displaystyle frac nabla F nabla F u infty phi x phi y phi z V text duvar cdot frac nabla F nabla F frac partial F partial t frac 1 nabla F Asagi inhiraf hizi Ing downwash speed w displaystyle w su sekilde yaklasik olarak hesaplanir w f t u f x displaystyle w frac partial f partial t u infty frac partial f partial x Basinc dagilimiBelirli bir hucum acisindaki bir kanat profili basinc dagilimi olarak adlandirilan bir duruma sahiptir Bu basinc dagilimi kanat profilinin etrafindaki tum noktalardaki basinc degerlerini ifade eder Genellikle bu dagilimlarin grafiklerinde negatif degerler grafikte daha yuksek konumda cizilir cunku kanat profilinin ust yuzeyindeki Cp displaystyle C p genellikle sifirin oldukca altinda olacak ve bu nedenle grafikteki en ust cizgi olacaktir Aerodinamik katsayilarla iliskiUc aerodinamik katsayinin tamami basinc katsayisi egrisinin kord boyunca integralidir Kaldirma katsayisi tamamen yatay yuzeylere sahip iki boyutlu bir kanat profili kesiti icin basinc katsayisi dagilimindan entegrasyon yoluyla veya dagilimdaki cizgiler arasindaki alanin hesaplanmasi ile belirlenebilir Bu ifade kaldirma yaklastirmasinin panel yontemi kullanilarak dogrudan sayisal entegrasyon icin uygun degildir cunku basinc kaynakli kaldirma yonunu dikkate almaz Bu denklem yalnizca sifir hucum acisi icin gecerlidir Cl 1xTE xLE xLExTE Cpl x Cpu x dx displaystyle C l frac 1 x TE x LE int limits x LE x TE left C p l x C p u x right dx burada Cpl displaystyle C p l alt yuzeydeki basinc katsayisidir Cpu displaystyle C p u ust yuzeydeki basinc katsayisidir xLE displaystyle x LE on kenarin konumudur xTE displaystyle x TE arka kenarin konumudur Alt yuzeydeki Cp displaystyle C p daha yuksek daha negatif oldugunda bu negatif bir alan olarak kabul edilir cunku bu durum kaldirma yerine asagi dogru kuvvet uretecektir Ayrica bakinizKaldirma katsayisi Surukleme katsayisiKaynakca 1975 Aerodynamics 3 6 Pitman Publishing Limited London 0 273 01120 0 Abbott and Von Doenhoff Theory of Wing Sections equation 2 24 Anderson John D Fundamentals of Aerodynamics 4th ed New York McGraw Hill 2007 219 https thesis library caltech edu 608 1 Scherer lr 1950 pdfDiger okumalarAbbott I H and Von Doenhoff A E 1959 Theory of Wing Sections Dover Publications Inc New York Standard Book No 486 60586 8 Anderson John D 2001 Fundamentals of Aerodynamic 3rd Edition McGraw Hill 0 07 237335 0
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans























