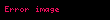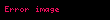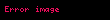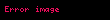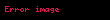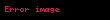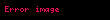Diofantos denklemi diğer bir adıyla Diophantine denklemleri adını M.S. 3. yüzyılda yaşadığı tahmin edilen Antik Yunan matematikçilerden Diofantos'dan alan değişkenleri ve katsayıları tam sayılar olan denklemlerdir. Diofantos Arithmetika adlı sadece 6 cildi günümüze ulaşan çalışmasında 130 denkleme (bugün Diofantos denklemleri olarak adlandırılan) ve bunların çözümlerine yer vermiştir.
Doğrusal denklemler
Basit doğrusal Diofantos denklemine örnekler aşağıdaki gibi verilebilinir;
- Örnek 1.1
Bu eşitlikte her bir x değeri için tek bir y çözümü vardır (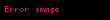
- (X, 1 − X) şeklindedir her X ∈ Z için
- Örnek 1.2
Bu defa x'in herhangi bir tam sayı olamayacağı fakat sadece tek sayı olabileceği görülüyor (
- (1-2y, y) şeklindedir her y ∈ Z için
- Örnek 1.3
Bu eşitliğin çözüm kümesi boş kümedir. Her 

- Genel doğrusal Diofantos denklemi
Şeklindedir. Burada a, b ve c tam katsayılarve
tam sayı değişkenlerdir.
Diğer Örnekler
Pisagor Denklemi
Genel bir örnek Pisagor denklemidir (Bakınız; Pisagor teoremi )
- Örnek 2.1.1
Buradatam sayıları dik üçgenin kenar uzunluklarını da temsil ettiği için Pisagor üçlemi olarak da adlandırılır.
Fermat Denklemi
(Bakınız; Fermat'nın son teoremi )
- Örnek 2.2.1
, n > 2
Bu eşitliğintam sayı değişkenlerinden en az birinin 0 olması durumu dışında çözümü yoktur.
Pell'in Denklemi
Bakınız
Bu denklem adını 17. yüzyıl İngiliz Matematikçi John Pell'den alır.
- Örnek 2.3.1
, n>0 ve n tam sayısı tam kare değildir
Kaynakça
- Özel
- Genel
- "Diophantine Equation". 30 Ekim 2012 tarihinde http://mathworld.wolfram.com/DiophantineEquation2ndPowers.html 11 Mayıs 2012 tarihinde Wayback Machine sitesinde . adresinden
- "Diophantine Equation". 30 Ekim 2012 tarihinde http://planetmath.org/encyclopedia/DiophantineEquation.html 8 Mart 2016 tarihinde Wayback Machine sitesinde . adresinden
- "Diophantine Equation". 30 Ekim 2012 tarihinde http://www.math.umass.edu/~gunnells/talks/abc.pdf 15 Haziran 2010 tarihinde Wayback Machine sitesinde . adresinden
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Diofantos denklemi diger bir adiyla Diophantine denklemleri adini M S 3 yuzyilda yasadigi tahmin edilen Antik Yunan matematikcilerden Diofantos dan alan degiskenleri ve katsayilari tam sayilar olan denklemlerdir Diofantos Arithmetika adli sadece 6 cildi gunumuze ulasan calismasinda 130 denkleme bugun Diofantos denklemleri olarak adlandirilan ve bunlarin cozumlerine yer vermistir Dogrusal denklemlerBasit dogrusal Diofantos denklemine ornekler asagidaki gibi verilebilinir Ornek 1 1x y 1 displaystyle x y 1 Bu esitlikte her bir x degeri icin tek bir y cozumu vardir y 1 x displaystyle y 1 x Bu esitligin cozum kumesi X 1 X seklindedir her X Z icinOrnek 1 2x 2y 1 displaystyle x 2y 1 Bu defa x in herhangi bir tam sayi olamayacagi fakat sadece tek sayi olabilecegi goruluyor x 1 2y displaystyle x 1 2y Bu esitligin cozum kumesi 1 2y y seklindedir her y Z icinOrnek 1 33x 6y 1 displaystyle 3x 6y 1 Bu esitligin cozum kumesi bos kumedir Her x displaystyle x ve y displaystyle y tam sayi secimi icin bu denklemin sol tarafi her zaman 3 un kati oldugu halde sag tarafi hicbir zaman 3 un kati olamaz Genel dogrusal Diofantos denklemiax by c displaystyle ax by c Seklindedir Burada a b ve c tam katsayilar x displaystyle x ve y displaystyle y tam sayi degiskenlerdir Diger OrneklerPisagor Denklemi Genel bir ornek Pisagor denklemidir Bakiniz Pisagor teoremi Ornek 2 1 1x2 y2 z2 displaystyle x 2 y 2 z 2 Burada x y z displaystyle x y z tam sayilari dik ucgenin kenar uzunluklarini da temsil ettigi icin Pisagor uclemi olarak da adlandirilir Fermat Denklemi Bakiniz Fermat nin son teoremi Ornek 2 2 1xn yn zn displaystyle x n y n z n n gt 2 Bu esitligin x y z displaystyle x y z tam sayi degiskenlerinden en az birinin 0 olmasi durumu disinda cozumu yoktur Pell in Denklemi Bakiniz Bu denklem adini 17 yuzyil Ingiliz Matematikci John Pell den alir Ornek 2 3 1x2 ny2 1 displaystyle x 2 ny 2 1 n gt 0 ve n tam sayisi tam kare degildirKaynakcaOzel Quick Martyn PDF Ingilizce University of St Andrews 25 Kasim 2011 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 30 Ekim 2012 Kirschenbaum Marni Alexandrian Algebra according to Diophantus Ruthgers 21 Mart 2015 tarihinde kaynagindan Erisim tarihi 28 Ekim 2012 Genel Diophantine Equation 30 Ekim 2012 tarihinde http mathworld wolfram com DiophantineEquation2ndPowers html 11 Mayis 2012 tarihinde Wayback Machine sitesinde adresinden Diophantine Equation 30 Ekim 2012 tarihinde http planetmath org encyclopedia DiophantineEquation html 8 Mart 2016 tarihinde Wayback Machine sitesinde adresinden Diophantine Equation 30 Ekim 2012 tarihinde http www math umass edu gunnells talks abc pdf 15 Haziran 2010 tarihinde Wayback Machine sitesinde adresinden
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans