EPR paradoksu, kuantum mekani─¤inin Kopenhag yorumuna kar┼¤─▒ erken ve etkili bir ele┼¤tiridir. Albert Einstein ve arkada┼¤lar─▒ ve Nathan Rosen (topluca EPR olarak bilinen) kuantum mekani─¤inin daha ├Čnce fark edilmemi┼¤ fakat belli sonu├¦lara sahip olan kabul edilmi┼¤ denklemlendirimini meydana ├¦─▒karan bir d├╝┼¤├╝nce deneyi haz─▒rlad─▒lar, ancak zamanla bu denklemlendirimler mant─▒ks─▒z g├Čr├╝nd├╝. A├¦─▒klanan senaryo kuantum dolan─▒kl─▒k olarak bilinen bir olay i├¦eriyordu.

Kuantum mekani─¤ine g├Čre, baz─▒ ko┼¤ullar alt─▒nda, ortakla┼¤a veya bireysel olan ├¦ift kuantum sistemleri, ├¦ift sistemde ger├¦ekle┼¤en deneylerin sonu├¦lar─▒n─▒n olas─▒l─▒klar─▒n─▒ kodlayan tek bir dalgan─▒n i┼¤leviyle tan─▒mlanabilir. A┼¤a─¤─▒da ele al─▒nan EPR makalesi yaz─▒ld─▒─¤─▒nda, yap─▒lan deneyler sonucu, bir deneyin sonucunun bazen tek bir tahmini olmad─▒─¤─▒ biliniyordu. Bu tip bir belirsizlik, bir ─▒┼¤─▒k s├╝zmesi yar─▒m g├╝m├╝┼¤lenmi┼¤ bir aynan─▒n ├╝zerine d├╝┼¤t├╝─¤├╝nde g├Čr├╝lebilir. I┼¤─▒k s├╝zmesinin yar─▒s─▒ yans─▒rken di─¤er yar─▒s─▒ ge├¦ecektir. E─¤er ─▒┼¤─▒k s├╝zmesinin ┼¤iddeti, tek bir foton ge├¦ene kadar indirgenirse, kuantum mekani─¤inde fotonun yans─▒mas─▒ veya ge├¦i┼¤i tahmin edilemez.
Bu etkinin rutin a├¦─▒klamas─▒ o zamanlar Heisenberg'in belirsizlik ilkesiyle sa─¤lanm─▒┼¤t─▒. Fiziksel nicelikler e┼¤lenik denilen ├¦iftler halinde gelir. Bu t├╝r e┼¤lenik ├¦iftlerinin ├Črnekleri aras─▒nda konumu ve farkl─▒ eksenler etraf─▒nda ├Čl├¦├╝len bir par├¦ac─▒─¤─▒n ve bile┼¤enlerinin devinirli─¤i verilebilir. Bir nicelik ├Čl├¦├╝ld├╝─¤├╝nde ve belirlendi─¤inde, birle┼¤mi┼¤ nicelikler belirsizle┼¤ir. Heisenberg bunu ├Čl├¦├╝mden kaynaklanan bir rahats─▒zl─▒k olarak a├¦─▒klam─▒┼¤t─▒r.
1935 y─▒l─▒nda yaz─▒lm─▒┼¤ EPR makalesi, bu a├¦─▒klaman─▒n yetersiz oldu─¤unu g├Čstermeyi ama├¦lam─▒┼¤t─▒r. A ve B olarak adland─▒r─▒lan iki dola┼¤─▒k par├¦ac─▒─¤─▒ dikkate ald─▒─¤─▒m─▒zda; A par├¦ac─▒─¤─▒n─▒n niceli─¤inin ├Čl├¦├╝lmesi, B par├¦ac─▒─¤─▒n─▒n e┼¤leni─¤inin niceli─¤inin hi├¦bir temas ve kar─▒┼¤─▒kl─▒k olmadan belirsizle┼¤mesine neden olur. Temel fikir, bir sistemin i├¦indeki iki par├¦ac─▒─¤─▒n kuantum durumlar─▒, her zaman ikisinin ortak durumundan ayr─▒┼¤amaz. Bunun bra-ket yaz─▒l─▒m─▒ndaki bir ├Črne─¤i ┼¤u ┼¤ekildedir;
Heisenberg belirsizlik ilkesi, bazen yerel olmayan denilen bir kuantum etkisinin klasik bir a├¦─▒klamas─▒n─▒n sa─¤lanmas─▒n─▒ ├¦abalad─▒. EPR'ye g├Čre bu durumun iki olas─▒ a├¦─▒klamas─▒ vard─▒. Par├¦ac─▒klar aras─▒nda ayr─▒m olsa bile ya aralar─▒nda bir etkile┼¤im vard─▒ ya da t├╝m olas─▒ ├Čl├¦├╝mlerin sonu├¦lar─▒ hakk─▒nda bilgiler par├¦ac─▒klarda mevcuttu.
EPR yazarlar─▒ ikinci a├¦─▒klamay─▒, baz─▒ kodlanm─▒┼¤ 'gizli de─¤i┼¤kenlerden' dolay─▒ tercih etmi┼¤lerdir. Bir etki an─▒nda bir uzakl─▒k boyunca yay─▒lan ilk a├¦─▒klama, g├Črelilik teorisi ile ├¦eli┼¤mekteydi. Daha sonra, kuantum mekani─¤inin kuralc─▒l─▒─¤─▒ndan dolay─▒ tamamlanmam─▒┼¤ oldu─¤u sonucuna vard─▒lar ├¦├╝nk├╝ bu tip gizli de─¤i┼¤kenlere kuantum mekani─¤inde yer yoktur.
Bell teoremi sonu├¦lar─▒ndaki ihlaller genellikle Einstein, Poldolsky ve Rosen taraf─▒ndan da varsay─▒lan Bell'in teoreminin hipotezlerinin bizim d├╝nyam─▒zda ge├¦erli olmamas─▒ndan anla┼¤─▒lmaktad─▒r. Konuyu ve konuyla ilgili deneyleri inceleyen Alain Aspect ve grubu gibi fizik├¦ilerin ├¦o─¤u, EPR ilk dikkat ├¦ekti─¤inde, kuantum teorisinin ├Čng├Črd├╝─¤├╝ gibi, EPR'nin tercih etti─¤i ŌĆ£yerel gizli de─¤i┼¤kenŌĆØ teorisini Bell e┼¤itsizliklerini ihlal etti─¤inden ├Čt├╝r├╝ ge├¦ersiz kabul etti.
EPR geli┼¤imlerinin tarihi
Bu konular─▒ ilk ortaya koyan makale, 1935 y─▒l─▒nda yay─▒nlanan "Fiziksel Ger├¦ekli─¤in Kuantum Mekaniksel Tan─▒m─▒ Tam Olarak D├╝┼¤├╝n├╝lebilir Mi?"'dir. Einstein kuantum mekanik bi├¦imcili─¤i a├¦─▒s─▒ndan ├Čl├¦├╝mlerle yorumlanarak ortaya ├¦─▒kanlar d─▒┼¤─▒ndaki nesnel fiziksel bir ger├¦ekli─¤in var oldu─¤u g├Čr├╝┼¤├╝n├╝ protesto etmi┼¤, kendi d├╝┼¤├╝ncesine daha ├¦ok uyan nedensellik teorisi i├¦in hayat─▒n─▒n sonuna kadar m├╝cadele etmi┼¤tir. Ancak, Einstein'─▒n ├Čl├╝m├╝nden sonra, bir EPR ka─¤─▒d─▒nda anlat─▒lan and─▒ran deneyler Frans─▒z bilim adamlar─▒ Lamehi-Rachti ve Mittig taraf─▒ndan 1976 y─▒l─▒nda Saclay N├╝kleer Ara┼¤t─▒rma Merkezinde ger├¦ekle┼¤tirilmi┼¤tir. Bu deneyler, yerel ger├¦ek├¦ilik fikrinin yanl─▒┼¤ oldu─¤unu g├Čstermi┼¤tir.
Kuantum mekani─¤i ve yorumlanmas─▒
Yirminci y├╝zy─▒l─▒n ba┼¤─▒ndan beri, kuantum kuram─▒, do─¤ru mezoskopik ve mikroskobik d├╝nyan─▒n fiziksel ger├¦ekli─¤ini a├¦─▒klayan birden fazla tekrarlanabilir fizik deneylerinde ba┼¤ar─▒l─▒ oldu─¤unu kan─▒tlam─▒┼¤t─▒r.
Kuantum mekani─¤i, atomunlar─▒ tan─▒mlayan ve bir ├Čl├¦├╝m cihaz─▒nda g├Čzlenen tayfi ├¦izgileri a├¦─▒klama amac─▒ ile geli┼¤tirilmi┼¤tir.Yirminci y├╝zy─▒l─▒n ba┼¤lar─▒nda iddial─▒ olmas─▒na ra─¤men, konuyla ilgili hen├╝z ciddi bir meydan okuma yap─▒lmam─▒┼¤t─▒r. Kuantum olaylar─▒n─▒n felsefi yorumlamas─▒, ancak, ba┼¤ka bir meseledir: kuantum mekani─¤inin matematiksel denklemlendirimini yorumlaman─▒n nas─▒l olaca─¤─▒n─▒n sorusu farkl─▒ felsefi g├Čr├╝┼¤lerden insanlar─▒n farkl─▒ cevaplar vermesini do─¤urmu┼¤tur.
Kuantum teorisi ve kuantum mekani─¤i belirleyici bir ┼¤ekilde tek ├Čl├¦├╝m sonu├¦lar─▒ vermemektedir. Kopenhag yorumlamas─▒ olarak bilinen kuantum mekani─¤i anlay─▒┼¤─▒na g├Čre, ├Čl├¦├╝mlerin dalga i┼¤levlerinin anl─▒k ├¦├Čkmesine neden olmas─▒, ├Čzdurumdaki kuantum sistemini betimler. Einstein, 1927 Solvay Konferans─▒nda bu ├¦├Čkmenin canland─▒rmas─▒n─▒ yapm─▒┼¤t─▒r. Deneyi, i├¦ y├╝zeyi alg─▒lan─▒m ekran─▒na sahip k├╝redeki k├╝├¦├╝k bir delikten elektron tan─▒mlamas─▒yla yapm─▒┼¤t─▒r. Bu deneyde elektronlar k├╝renin i├¦ y├╝zeyiyle yayg─▒n olarak da─¤─▒n─▒k bir ┼¤ekilde temasta bulunmu┼¤tur. Ancak bu elektronlar dalga cephelerinin girdi─¤i noktadan b├╝t├╝n y├Čnlere geni┼¤lemesiyle a├¦─▒klanabilir. G├╝nl├╝k ya┼¤amdan da anla┼¤─▒laca─¤─▒ gibi bir dalga alg─▒lan─▒m ekran─▒nda geni┼¤ bir b├Člge kaplar fakat elektronlar─▒n tek noktalarda ekrana bir etkisi olacakt─▒r ve sonunda kendi ├Čzde┼¤ dalga fonksiyonlar─▒ taraf─▒ndan a├¦─▒klanan olas─▒l─▒klar─▒ do─¤rultusunda bir model olu┼¤turacakt─▒r. Einstein, konumuna ba─¤l─▒ olarak neden her elektronun dalgas─▒n─▒n ├Čn cephesinin ├¦├Čkt├╝─¤├╝n├╝, niye elektronlar─▒n y├╝zey ├╝zerindeki enerji gibi lo┼¤ olmas─▒ yerine tek parlak p─▒r─▒ldan─▒mlar olarak g├Čr├╝nmesini ve neden tek bir elektronun herhangi bir nokta yerine sabit tek bir noktada bulundu─¤unu sorar. Elektronlar─▒n davran─▒┼¤─▒, b├╝t├╝n olas─▒ noktalara g├Čnderilmi┼¤ fakat biri d─▒┼¤─▒nda t├╝m hepsini ge├¦ersiz k─▒lan baz─▒ sinyallerin izlenimini verir. Di─¤er bir deyi┼¤le, t├╝m noktalar haricinde tek bir nokta se├¦ilebilir.
Einstein'─▒n kar┼¤─▒tl─▒─¤─▒
Einstein Kopenhag yorumunun en ├Čnemli rakibi oldu. Onun g├Čr├╝┼¤├╝ne g├Čre, kuantum mekani─¤i tamamlanmam─▒┼¤t─▒. Bunu yorumlayan, John von Neumann ve David Bohm gibi di─¤er yazarlar orijinal k├ó─¤─▒t a├¦─▒k├¦a iddia edilmemi┼¤, rastgele yap─▒lan ├Čl├¦├╝m sonu├¦lar─▒ndan 'gizli' de─¤i┼¤kenleri sorumlu tutmu┼¤tur.
1935 EPR makalesi felsefi tart─▒┼¤may─▒ fiziksel bir tart─▒┼¤man─▒n i├¦ine s─▒k─▒┼¤t─▒rm─▒┼¤t─▒r. Yazarlar bir ├Čl├¦├╝m├╝n sonucu olan verilmi┼¤ ├Čzg├╝l bir deneyde ├Čl├¦├╝m ger├¦ekle┼¤meden ├Čnce ger├¦eklik unsuru denilen bir ┼¤eyin ger├¦ek d├╝nyada var oldu─¤unu iddia etmi┼¤lerdir. Yazarlar, ger├¦ekli─¤in bu unsurlar─▒n─▒n her uzayzamandaki belli bir noktaya ait oldu─¤unu yani yerel oldu─¤unu varsaymaktad─▒r. Her element sadece uzay-zaman─▒n (yani, ge├¦mi┼¤in) onun ─▒┼¤─▒k konisinin gerisinde bulunan olaylardan etkilenmi┼¤tir. Bu iddialar art─▒k yerel ger├¦ek├¦ilik olarak bilinen te┼¤kil do─¤as─▒ hakk─▒nda varsay─▒mlar ├╝zerine kurulmu┼¤tur.
EPR makalesi s─▒k s─▒k Einstein'─▒n g├Čr├╝┼¤lerinin tam bir ifadesi olarak al─▒nm─▒┼¤ olsa da, ba┼¤ta Einstein ve Rosen ile Geli┼¤mi┼¤ ├ćal─▒┼¤ma Enstit├╝s├╝ndeki g├Čr├╝┼¤melere dayanarak, Podolsky taraf─▒ndan yaz─▒lm─▒┼¤t─▒r. Einstein, daha sonra Erwin Schr├Čdinger'e "bu, benim normalde istedi─¤im gibi bir sonu├¦ vermedi, daha ziyade, ├Čnemli ┼¤ey, tabiri caizse, bi├¦imcilik taraf─▒ndan bo─¤uldu." demi┼¤tir. 1936 y─▒l─▒nda, Einstein yerel ger├¦ek├¦i fikirlerinin bir bireysel hesab─▒n─▒ sundu.
Paradoksun tan─▒m─▒
Orijinal EPR paradoksu, kuantum mekani─¤inin bir tahmini olan bir kuantum par├¦ac─▒─¤─▒n─▒n konumunun ve devinirli─¤inin ayn─▒ anda bilinememesine meydan okur. Bu meydan okuma, ba┼¤ka fiziksel ├Čzelliklerin di─¤er ├¦iftlerinin geni┼¤lemesiyle olabilir.
EPR Makalesi
Orijinal makale, etkile┼¤ime ge├¦mesine izin verilen iki sisteme ne olaca─¤─▒n─▒ ve bir s├╝re sonra etkile┼¤im kalmad─▒─¤─▒nda neler olaca─¤─▒n─▒ tan─▒mlama amac─▒ g├╝tm├╝┼¤t├╝r. Kumar'─▒n s├Čzleriyle bu, A ve B olan iki par├¦ac─▒─¤─▒n k─▒saca etkile┼¤imde olmas─▒ ve daha sonra farkl─▒ y├Čnlere hareket etmesi olarak tan─▒mlanabilir. Heisenberg'in belirsizlik ilkesine g├Čre, devinirli─¤i ve B par├¦ac─▒─¤─▒n─▒n tam olarak konumunu ayn─▒ anda ├Čl├¦mek m├╝mk├╝n de─¤ildir fakat Kumar'a g├Čre A par├¦ac─▒─¤─▒n─▒n kesin konumunu belirlemek m├╝mk├╝nd├╝r. Bu nedenle, ├Čl├¦├╝mler sonucu A'n─▒n bilinen kesin konumu yard─▒m─▒yla B'nin kesin konumu bulunabilir. Ayr─▒ca, A par├¦ac─▒─¤─▒n─▒n devinirli─¤i ├Čl├¦├╝lebildi─¤inden, B par├¦ac─▒─¤─▒n─▒nkini de A'ya ba─¤l─▒ olarak bulmak m├╝mk├╝nd├╝r. Kumar, bunu ┼¤u ┼¤ekilde yazm─▒┼¤t─▒r; ŌĆ£EPR, B par├¦ac─▒─¤─▒ e┼¤ zamanl─▒ olarak kesin ve ger├¦ek bir devinirlik ve konum de─¤erine sahiptir yarg─▒s─▒n─▒ kan─▒tlam─▒┼¤ ve savunmu┼¤tur.ŌĆØ EPR, B par├¦ac─▒─¤─▒ fiziksel olarak rahats─▒z olma olas─▒l─▒─¤─▒ olmadan, par├¦ac─▒k A ├╝zerinde yap─▒lan ├Čl├¦├╝mler sonucunda B'nin ya devinirli─¤inin ya da pozisyonunun kesin de─¤erlerini bulmay─▒ ama├¦lad─▒.
EPR Kuantum Mekani─¤i ger├¦ek uygulama aral─▒─¤─▒n─▒ sorgulamak i├¦in bir paradoks yaratmaya ├¦al─▒┼¤t─▒. Bu paradoks; Kuantum teorisi iki de─¤erin de par├¦ac─▒k i├¦in tahmin edilemez olmas─▒n─▒ ve hen├╝z EPR d├╝┼¤├╝nce deneyinin hepsinin belirli de─¤erlere sahip olmas─▒ gerekti─¤ini g├Čstermesini i├¦eriyordu. EPR ka─¤─▒d─▒: "Biz, fiziksel ger├¦ekli─¤in kuantum mekaniksel tan─▒m─▒n─▒n tam olarak dalga i┼¤levleri taraf─▒ndan a├¦─▒klanamayaca─¤─▒ sonunu kabul etmek zorunda kal─▒yoruz.ŌĆØ demi┼¤tir.
EPR ka─¤─▒d─▒ ┼¤u s├Čz ile sonlan─▒r: Biz b├Čylece dalga fonksiyonun fiziksel ger├¦ekli─¤in tam bir a├¦─▒klamas─▒n─▒ yapamad─▒─¤─▒n─▒ g├Čstersek de, biz b├Čyle bir a├¦─▒klaman─▒n var olup olmad─▒─¤─▒ sorusuna kesin bir cevap bulamad─▒k. Biz b├Čyle bir teori m├╝mk├╝n oldu─¤una, yine de, inan─▒yoruz.
Dola┼¤─▒k durumda ├Čl├¦├╝mler
Elimizde elektron-pozitron ├¦iftlerini yayan bir kaynak var ve Alice ad─▒ndan bir g├Čzlemcinin oldu─¤u A noktas─▒na elektron, Bob ad─▒nda bir g├Čzlemci bulunan B noktas─▒na da pozitron g├Čnderiyoruz. Kuantum mekani─¤ine g├Čre, kayna─¤─▒m─▒z─▒, yay─▒lan her ├¦iftin tekli f─▒r─▒l ad─▒ verilen kuantum durumunu i┼¤gal edece─¤i ┼¤ekilde ayarlayabiliriz. B├Čylece, bu par├¦ac─▒klar dola┼¤─▒kt─▒r diyebiliriz. Bu, durum 1 ve durum 2 olarak adland─▒rd─▒─¤─▒m─▒z iki kuantum ├¦ak─▒┼¤mas─▒ durumu olarak g├Čr├╝lebilir. Durum 1de, pozitif z ekseninde bir f─▒r─▒l─▒ olan elektron ve negatif z ekseninde bir f─▒r─▒la sahip pozitron vard─▒r. Durum 2de ise, elektron negatif z ekseninde bir f─▒r─▒la sahipken, pozitif z ekseninde pozitron bir f─▒r─▒la sahiptir. Bundan dolay─▒, ├Čl├¦├╝m yapmadan tekli f─▒r─▒l durumundaki bir par├¦ac─▒─¤─▒n durum f─▒r─▒l─▒n─▒ belirlemek m├╝mk├╝n de─¤ildir.

Art─▒k, Alice z ekseni etraf─▒ndaki f─▒r─▒l─▒ ├Čl├¦er ve +z veya -z olmak ├╝zere iki muhtemel sonu├¦ elde edebilir. E─¤er elde etti─¤i sonu├¦ +z ise; kuantum mekani─¤inin Kopenhag yorumlamas─▒na g├Čre sistemin kuantum durumu durum 1de ├¦├Čker. Kuantum durumu sistemde ger├¦ekle┼¤en her t├╝rl├╝ ├Čl├¦├╝m├╝n sonucunu belirler. Bu durumda, e─¤er Bob z ekseni etraf─▒nda sonradan ├Čl├¦├╝m yaparsa, bulaca─¤─▒ sonu├¦ -z ekseninde olur. Ayn─▒ ┼¤ekilde, e─¤er Alice -z ekseninde sonu├¦ al─▒rsa, Bob +z ekseninde bir sonu├¦ al─▒r.
├¢zellikle z eksenini se├¦memizin belirli bir nedeni yoktur, kuantum mekani─¤ine g├Čre tekli f─▒r─▒l durumu x eksenini g├Čsteren f─▒r─▒l durumunun ├¦ak─▒┼¤mas─▒ da e┼¤it olur. E─¤er Alice ve Bob f─▒r─▒l─▒ x ekseninde ├Čl├¦meye karar verirse, buna durum 1a ve durum 2a deriz. Durum 1a'da, Alice'in elektronu +x f─▒r─▒l─▒na sahipken, Bob'un pozitronu -x f─▒r─▒l─▒na sahiptir. Durum 2a'da ise, Alice'in elektronu -x f─▒r─▒l─▒na sahipken, Bob'un pozitronu +x f─▒r─▒l─▒na sahiptir. Bundan dolay─▒, E─¤er Alice +x ├Čl├¦erse, sistem durum 1ada ├¦├Čker ve Bob -x sonucunu elde eder. E─¤er Alice -x ├Čl├¦erse, sistem durum 2a'da ├¦├Čker ve Bob +x sonucunu elde eder.
Herhangi bir eksende f─▒r─▒llar─▒ ├Čl├¦├╝l├╝rse, sonu├¦ her zaman birbirlerinin tersi olur. Bu durum, sadece par├¦ac─▒klar birbirlerine ba─¤l─▒ysa a├¦─▒klanabilir. Ya her eksende kesin olarak farkl─▒ f─▒r─▒la sahip ┼¤ekilde yarat─▒lm─▒┼¤lard─▒r (gizli de─¤i┼¤ken tart─▒┼¤mas─▒) ya da birbirlerine ba─¤l─▒lard─▒r ve bu y├╝zden bir elektron di─¤erinin eksenin hangi taraf─▒nda oldu─¤unu hissediyordur ve onun kar┼¤─▒t sonucunu al─▒yorudur (dola┼¤─▒kl─▒k tart─▒┼¤mas─▒). Ayr─▒ca, e─¤er iki par├¦ac─▒─¤─▒n farkl─▒ eksenler boyunca f─▒r─▒llar─▒ ├Čl├¦├╝l├╝yorsa, x ekseninde elektron f─▒r─▒l─▒ ├Čl├¦├╝ld├╝─¤├╝nde (ve x eksenindeki pozitronun f─▒r─▒l─▒ yok say─▒ld─▒─¤─▒nda), z eksenindeki pozitronun f─▒r─▒l─▒ kesin de─¤ildir ├¦├╝nk├╝ ├Čl├¦├╝m yerini alm─▒┼¤t─▒r ve zaten ikinci bir eksende f─▒r─▒l─▒ mevcuttur. Buna ra─¤men, deneyler taraf─▒ndan onaylanan kuantum mekani─¤i hakk─▒ndaki varsay─▒mlar, herhangi bir gizli de─¤i┼¤ken teorisiyle a├¦─▒klanamaz. Bu, Bell teoreminde g├Čsterilmi┼¤tir.
Kuantum mekani─¤inde,Heisenberg belirsizlik ilkesine g├Čre iki de─¤i┼¤ken i├¦in de kuantum durumu kesin bir sonuca sahip olamaz ve bu durum x-f─▒r─▒l─▒ ve z-f─▒r─▒l─▒ ŌĆ£uyumsuz g├ČzlemlenenlerdirŌĆØ anlam─▒na gelir. Alice'in z-f─▒r─▒l─▒ ├Čl├¦t├╝─¤├╝n├╝ varsayal─▒m ve buldu─¤u sonu├¦ +z olsun, bu durumda kuantum durumu durum 1de ├¦├Čker. ┼×imdi, z-f─▒r─▒l─▒n─▒ ├Čl├¦mek yerine, Bob x-f─▒r─▒l─▒n─▒ ├Čl├¦s├╝n. Kuantum mekani─¤ine g├Čre, e─¤er sistem durum 1de ise, Bob'un x-f─▒r─▒l ├Čl├¦├╝m├╝ %50 ihtimalle +xde olabilir ya da %50 ihtimalle -xde olabilir. Bob'un kendisi ├Čl├¦├╝m yapana kadar, nas─▒l bir sonu├¦ elde edilece─¤ini tahmin etmek imk├óns─▒zd─▒r.
Bu, konunun d├Čn├╝m noktas─▒d─▒r. Bob pozitronun x-f─▒r─▒l─▒n─▒ ├Čl├¦t├╝─¤├╝nde, kesin bir sonuca ula┼¤abilir ├¦├╝nk├╝ kendi par├¦ac─▒─¤─▒n─▒ rahats─▒z etmemi┼¤tir. Bob'un pozitronu %50 ihtimalle +x veya -x'dedir ve kesin bir sonu├¦ yoktur ├¦├╝nk├╝ Bob'un pozitronu Alice'in elektronunu bilir ve Alice'in elektronu bilinip ├Čl├¦├╝ld├╝─¤├╝ i├¦in Bob'un elektronunun spini hakk─▒nda kesin bir bilgi elde edemeyiz.
Kopenhag yorumuna g├Čre, dalga i┼¤levi ├Čl├¦├╝m yap─▒ld─▒─¤─▒ zaman ├¦├Čker ve bu y├╝zden belli bir uzakl─▒kta bir etki olmal─▒d─▒r veya pozitron bilmesi gerekenden daha fazlas─▒n─▒ bilmelidir.
Paradoksun ├Čzeti
─░lk par├¦ac─▒─¤─▒n fiziksel ├Čl├¦├╝mleri kendi konumunda devinirli─¤e etkisi kesin de─¤ildir fakat ilk par├¦ac─▒─¤─▒n devinirli─¤ini ├Čl├¦mek ├Čb├╝r├╝n├╝n konumunun kesinli─¤ini etkiler. Einstein, Podolsky ve Rosen, ikinci par├¦ac─▒─¤─▒n nas─▒l kesin olmayan konumuna ra─¤men kesin bir devinirli─¤e sahip oldu─¤unu sorgulad─▒. Bir par├¦ac─▒k di─¤eriyle uzayda ileti┼¤im halinde oldu─¤undan, bu bir ŌĆ£paradoksturŌĆØ.
Bu arada, Bell, f─▒r─▒l─▒ kendi ├Črne─¤inde kulland─▒ fakat kuantum mekani─¤inde g├Čzlemlenebilirler denilen bir├¦ok ├¦e┼¤it fiziksel nicelik kullan─▒l─▒yordu. EPR ka─¤─▒d─▒, bu g├Čzlemlenebilirlerin devinirli─¤i i├¦in kullan─▒l─▒yordu. EPR plan─▒n─▒n deneysel ger├¦ekle┼¤tirmeleri genellikle foton kutupla┼¤mas─▒nda kullan─▒yor ├¦├╝nk├╝ kutupla┼¤m─▒┼¤ fotonlar─▒n haz─▒rlanmas─▒ ve ├Čl├¦├╝lmesi kolayd─▒r.
EPR deneylerindeki yerellik
Yerellik ilkesi, bir yerde meydana gelen fiziksel i┼¤lemlerin ba┼¤ka bir yerdeki ger├¦eklik unsurlar─▒ ├╝zerinde bir etkisinin olmamas─▒ gerekti─¤ini belirtir. ─░lk bak─▒┼¤ta, bu bilgiler nedenselli─¤i ihlal etmeden ─▒┼¤─▒k h─▒z─▒ndan daha h─▒zl─▒ iletilmeyen bilgileri savunan ├Čzel g├Črelili─¤in sonu├¦lar─▒ hakk─▒nda makul bir varsay─▒m gibi g├Čr├╝n├╝yordu. Genellikle nedenselli─¤i ihlal eden herhangi bir teori de i├¦ten tutars─▒z olaca─¤─▒ndan, yarars─▒z olaca─¤─▒ d├╝┼¤├╝n├╝lmektedir.
Kuantum mekani─¤i ve klasik tan─▒mlar─▒n birle┼¤tirmek i├¦in olan ola─¤an kurallar, nedensellik yasas─▒n─▒ ihlal etmeden yerellik ilkesini ihlal etmektedir. Nedensellik korunmaktad─▒r ├¦├╝nk├╝ Alice'in Bob'un ├Čl├¦├╝m eksenini y├Čnlendirerek mesaj iletmesinin ba┼¤ka bir yolu yoktur. Alice hangi ekseni kullan─▒rsa kullans─▒n, %50 oran─▒nda + veya ŌĆō sonu├¦ elde etme olas─▒l─▒─¤─▒ vard─▒r ve kuantum mekani─¤ine g├Čre temel olarak hangi sonucu alaca─¤─▒n─▒ etkilemesi imk├óns─▒zd─▒r. Ayr─▒ca, Bob sadece bir kez kendi ├Čl├¦├╝m├╝n├╝ yapabilir ├¦├╝nk├╝ kuantum mekani─¤inin temel ├Čzelli─¤i ald─▒─¤─▒ elektronlar─▒n milyon tane kopyas─▒n─▒ yapmas─▒n─▒, hepsine tek tek f─▒r─▒l ├Čl├¦├╝m├╝ yapmas─▒n─▒ ve sonu├¦lar─▒n istatistiksel da─¤─▒l─▒m─▒na bakmas─▒n─▒ imk├óns─▒z k─▒lar. Bu nedenle, e─¤er sadece bir ├Čl├¦├╝m yapmas─▒na izin verilirse, + veya ŌĆō sonu├¦ bulmas─▒ Alice'le ayn─▒ eksende olup olmamas─▒na ba─¤l─▒ olmadan %50 ┼¤ans─▒ oldu─¤unu g├Čr├╝r├╝z.
Yine de, yerellik ilkesi fiziksel sezgilere g├╝├¦l├╝ bir ┼¤ekilde hitap etmi┼¤tir ve Einstein, Podolsky ve Rosen bu y├╝zden bu teoriyi terk etmek istemiyorlard─▒. Einstein, kuantum mekaniksel tahminlerle ŌĆ£bir noktada ├╝rk├╝t├╝c├╝ŌĆØ diyerek dalga ge├¦mi┼¤tir. Bu nedenle, kuantum mekani─¤inin hen├╝z tamamlanmam─▒┼¤ olmas─▒yla sonu├¦land─▒rm─▒┼¤lard─▒r.
Son y─▒llarda ise, EPR'nin ula┼¤t─▒─¤─▒ sonu├¦ yerellik anlamadaki geli┼¤melerden ve kuantumun elveri┼¤li olmamas─▒ndan ┼¤├╝phe uyand─▒rm─▒┼¤t─▒r. Yerellik kelimesi, fizikte bir├¦ok anlama sahiptir. ├¢rne─¤in, kuantum alan teorisinde "yerellik" uzay─▒n de─¤i┼¤ik noktalar─▒ndaki kuantum alanlar─▒n─▒n birbirleriyle etkile┼¤imde olmamalar─▒ anlam─▒na gelir. Ancak, bu anlamda "yerel" olan kuantum alan teorileri EPR taraf─▒ndan tan─▒mlanan yerellik ilkesine ayk─▒r─▒ g├Čr├╝nmektedir, ama yine de daha genel anlamda yerelli─¤i ihlal etmezler. Dalga i┼¤levinin ├¦├Čk├╝┼¤├╝, kuantum elveri┼¤sizli─¤inin epifenomeni olarak g├Čr├╝lebilir. Temel davran─▒┼¤ yerel nedenselli─¤i ihlal etmedi─¤inden, bu ger├¦ek ya da belirgin olsun, dalga fonksiyonu ├¦├Čk├╝┼¤├╝ ek bir etki yapar. Yukar─▒daki ├Črnekte belirtilen nedenle, ne EPR deneyinim ne de herhangi bir kuantum deneyinin g├Čsterilmesinin ─▒┼¤─▒k sinyalinden h─▒zl─▒ olmas─▒ m├╝mk├╝n de─¤ildir.
Paradoksun ├¦├Čz├╝m├╝
Gizli de─¤i┼¤kenler
EPR paradoksunu ├¦├Čzmek i├¦in ├¦e┼¤itli yollar vard─▒r. EPR taraf─▒ndan ├Čnerilen bir tanesi, kuantum mekani─¤idir, deneysel senaryolarda ├¦e┼¤itli ba┼¤ar─▒lar elde etmesine ra─¤men, asl─▒nda tamamlanmam─▒┼¤ bir teoridir. Di─¤er bir deyi┼¤le, kuantum mekani─¤i (bir derece ba┼¤ar─▒l─▒ bir de olsa) istatistiksel yakla┼¤─▒m gibi davranan do─¤an─▒n hen├╝z ke┼¤fedilmemi┼¤ baz─▒ teorileri vard─▒r. Kuantum mekani─¤inin aksine, daha tam bir teori t├╝m "ger├¦eklik unsurlar─▒na" kar┼¤─▒l─▒k gelen de─¤i┼¤kenleri i├¦erebilir. Heisenberg belirsizlik ilkesi, yani "iletmez kuantum g├Čzlenebilirlerinin" g├Čzlenen etkilerine yol vermek i├¦in bu de─¤i┼¤kenler ├╝zerinde hareket eden baz─▒ bilinmeyen mekanizmalar olmal─▒d─▒r. B├Čyle bir teoriye gizli de─¤i┼¤ken teorisi denir.
Bu fikir g├Čstermek i├¦in, yukar─▒daki d├╝┼¤├╝nce deneyi i├¦in ├¦ok basit bir gizli de─¤i┼¤ken teorisini haz─▒rlayabiliriz. Bir kaynaktan yay─▒lan kuantum tekli-f─▒r─▒l durumu do─¤ru fiziksel durum i├¦in x-f─▒r─▒l─▒ ve z-f─▒r─▒l─▒n─▒n kesin de─¤eri i├¦in yakla┼¤─▒k bir tan─▒m olu┼¤turur. Bu "ger├¦ek" durumlarda, Bob'a giden pozitron her zaman Alice'e giden elektronun ters f─▒r─▒l de─¤erine sahip olacakt─▒r, ancak aksi bir durumda de─¤erler tamamen rastgele olacakt─▒r. ├¢rne─¤in, kaynak taraf─▒ndan yay─▒lan ilk ├¦ift "Alice'e (+z,-x) ve Bob'a (-z, +x)" olabilir, bir sonraki ├¦ift ise "Alice'e (-z,-x) ve Bob'a (+z, +x) "ve benzerleri olabilir. Bu nedenle, Bob'un ├Čl├¦me ekseni, Alice'inki ile ayn─▒ hizada ise, Bob mutlaka Alice ne gelirse tersini alacak; aksi halde, Bob e┼¤it olas─▒l─▒kla "+" veya "-" al─▒cakt─▒r.
├¢l├¦├╝mlerimizi z ve x eksenleriyle s─▒n─▒rlad─▒─¤─▒m─▒z─▒ varsayarsak, b├Čyle bir gizli de─¤i┼¤ken teorisi kuantum mekani─¤inden deneysel olarak ay─▒rt edilemez. Ger├¦ekte, Alice ve Bob'un kendi ├Čl├¦├╝mlerini yapt─▒─¤─▒ sonsuz say─▒da eksen olabilir, bu y├╝zden sonsuz say─▒da ba─¤─▒ms─▒z gizli de─¤i┼¤kenler olmas─▒ gerekir. Ancak, bu ciddi bir sorun de─¤ildir ├¦├╝nk├╝ biz gizli de─¤i┼¤ken teorisini ├¦ok basit bir ┼¤ekilde ba─¤─▒nt─▒sal yazd─▒k ve daha sofistike bir teorinin bu konuda yama yapmas─▒ m├╝mk├╝n olabilir. Bu gizli de─¤i┼¤kenlerin fikrinde ├¦ok daha ciddi bir sorun oldu─¤unu ortaya ├¦─▒k─▒yor.
Bell e┼¤itsizlikleri
1964 y─▒l─▒nda, , EPR d├╝┼¤├╝nce deneyindeki kuantum mekani─¤inin tahminlerinin gizli de─¤i┼¤ken teorileriyle (yerel gizli de─¤i┼¤ken kuramlar─▒n─▒n) ├Čnemli ├Čl├¦├╝de farkl─▒ oldu─¤unu g├Čsterdi. Kabaca s├Čylemek gerekirse, kuantum mekani─¤inin di─¤er eksenlerde yap─▒lan ├Čl├¦├╝m sonu├¦lar─▒n─▒n istatistiksel ba─¤─▒nt─▒s─▒, gizli de─¤i┼¤ken teorilerindekinden daha g├╝├¦l├╝d├╝r. Bu farkl─▒l─▒klar, e┼¤itsizlik ili┼¤kilerini kullanan "Bell e┼¤itsizlikleri" olarak bilinen deneysel saptanabilen prensiplerdir. Eberhard taraf─▒ndan daha sonraki ├¦al─▒┼¤malarda Bell'in e┼¤itsizliklerine ├Čnc├╝l├╝k eden gizli de─¤i┼¤ken kuramlar─▒n─▒n yerelli─¤i ve kar┼¤─▒-olgusal kesinlik ├Čzelli─¤i g├Čsterilmi┼¤tir. Bu ilkelerin ge├¦erli oldu─¤u herhangi bir teori e┼¤itsizlikleri ├╝retir. Arthur Fine sonradan e┼¤itsizlikleri tatmin eden herhangi bir teorinin, yerel gizli de─¤i┼¤ken teorisi ile modellenebilir oldu─¤unu g├Čstermi┼¤tir.
Bell'in k├ó─¤─▒t yay─▒nlanmas─▒ndan sonra, Bell e┼¤itsizliklerini test etmek i├¦in ├¦e┼¤itli deneyler icat edildi. Bunlar genellikle foton kutupla┼¤mas─▒ ├Čl├¦├╝mlerine dayan─▒yordu. Bug├╝ne kadar yap─▒lan t├╝m deneylerin standart kuantum mekani─¤i teorisinin ├Čng├Čr├╝leri do─¤rultusunda oldu─¤u bulunmu┼¤tur.
Ancak Bell'in teoremi t├╝m olas─▒ felsefi olarak realist olan teoriler i├¦in ge├¦erli de─¤ildir. Kuantum mekani─¤inin felsefi ger├¦ek├¦ili─¤in t├╝m kavramlar─▒ ile tutars─▒z olmas─▒ yayg─▒n bir yan─▒lg─▒d─▒r. Kuantum mekani─¤inin realistik yorumlamas─▒ m├╝mk├╝nd├╝r, fakat yukar─▒da tart─▒┼¤─▒ld─▒─¤─▒ gibi, bu tip yorumlamalar yerelli─¤i ya da kar┼¤─▒-olgusal kesinli─¤i reddeder. Ana fizik, kar┼¤─▒-olgusal kesinli─¤i reddeden ger├¦ek├¦ilik kavram─▒n─▒ korumak i├¦in u─¤ra┼¤ verirken, yerelli─¤i tutmay─▒ da tercih eder. B├Čyle genel realist yorumlar─▒n ├Črnekleri, tutarl─▒ ge├¦mi┼¤lerini yorumlanmas─▒ ve ilk kez 1986 y─▒l─▒nda John G. Cramer taraf─▒ndan ├Čnerilen i┼¤lem yorumudur. Fine'─▒n ├¦al─▒┼¤malar─▒ g├Čsterdi ki, yerelli─¤i alarak, iki istatistiksel de─¤i┼¤ken olan kar┼¤─▒-olgusal kesinlikler tutars─▒z bir ┼¤ekilde ili┼¤kilidir ve bu t├╝r senaryolar olmas─▒na ra─¤men, daha gizemli senaryolar─▒n verilmesi ile tutars─▒zl─▒k kar┼¤─▒-olgusal kesinlik 'sezgilerde' g├Čr├╝nebilir.
Yerelli─¤in ihlalin, ├Čzel g├Črelilik ile ba─¤da┼¤t─▒rmak zordur ve nedensellik ilkesi ile uyumsuz oldu─¤u d├╝┼¤├╝n├╝lmektedir. Ancak, Schr├Čdinger denkleminin ┼¤artlar─▒n─▒ biri olarak tan─▒mlanan 'kuantum potansiyeli' ┼¤eklinde bir varsay─▒m─▒ yerel olmayan mekanizmas─▒ tan─▒t─▒l─▒rken, kuantum mekani─¤inin Bohm yorumlanmas─▒, kar┼¤─▒-olgusal kesinlik├¦e tutarl─▒d─▒r. Baz─▒ bu alanda ├¦al─▒┼¤anlar ger├¦ek deneylerde ka├¦amaklar─▒ s├Čm├╝ren gizli de─¤i┼¤ken teorisini ba─¤─▒nt─▒sal olarak yazmay─▒ denemi┼¤tir.
Ayr─▒ca, yerel gizli de─¤i┼¤kenleri olmayan bireysel EPR benzeri deneylerin a├¦─▒klamas─▒ da vard─▒r. ├¢rnekler David Bohm ve Lucien Hardy taraf─▒ndan ├Čnerilebilir.
Einstein'─▒n saf cebirsel teoriye inanc─▒
Kuantum mekani─¤inin Bohm yorumlanmas─▒na g├Čre, evrenin durumunun, kuantum dalga i┼¤levleri ├¦├Čkmeden zaman i├¦inde sorunsuzca geli┼¤ti─¤i varsay─▒lmaktad─▒r. Kopenhag yorumlanmas─▒ i├¦in olu┼¤an sorunlardan biri dalga i┼¤levinin ├¦├Čk├╝┼¤├╝n├╝n tan─▒mlanmas─▒d─▒r. Einstein kuantum mekani─¤inin fiziksel olarak eksik ve mant─▒ksal olarak yetersiz oldu─¤unu ileri s├╝rm├╝┼¤t├╝r. "G├Črelili─¤in Anlam─▒"nda Einstein, ŌĆ£Birisi neden ger├¦ekli─¤i s├╝rekli bir alanda a├¦─▒klanamayaca─¤─▒na iyi bir neden versin.ŌĆØ demi┼¤tir. Kuantum olaylar─▒na bak─▒ld─▒─¤─▒nda, sonlu bir enerjinin sonlu bir sistemi tamamen kuantum numaralar─▒ denilen sonlu bir dizi rakamla tarif edilebilir. Bu, bir s├╝reklilik teorisi i├¦in uygun olarak g├Čr├╝lmemektedir ve ger├¦ekli─¤in temsili i├¦in bir cebirsel teori bulma giri┼¤imine neden olmaktad─▒r. Ama hi├¦ kimse bu tip bir teori i├¦in bir temel bulamam─▒┼¤t─▒r."E─¤er zaman, mekan ve enerji Planck ├Čl├¦e─¤inde alt tabakadan t├╝retilmi┼¤ ikincil ├Čzellikleri ise (Bell'in teoremi hala ge├¦erli olsa da), Einstein'─▒n varsay─▒msal cebirsel sistemi EPR paradoksunu ├¦├Čzmek i├¦in yeterli olabilir. Fredkin'in Sonlu Do─¤a Hipotezi'nde Edward Fredkin, Einstein'─▒n varsay─▒msal cebirsel sistemi i├¦in bir bilgi temeli ├Čnerdi. E─¤er fiziksel ger├¦eklik tamamen sonlu ise, Kopenhag yorumu Planck ├Čl├¦e─¤inde, bir bilgi i┼¤lem sistemine bir yakla┼¤─▒m olabilir.
"Kabul edilebilir teoriler" ve deneyler
Durumun bug├╝nk├╝ g├Čr├╝┼¤├╝ne g├Čre, kuantum mekani─¤i kesin bir dille kabul edilebilir herhangi bir fiziksel teorinin "yerel ger├¦ek├¦ili─¤i" yerine getirmesi gerekti─¤ini savunan Einstein'─▒n yerel felsefi ├Čnermesiyle ├¦eli┼¤mektedir.
1935 y─▒l─▒nda yaz─▒lan EPR ka─¤─▒d─▒nda, yazarlar kuantum mekani─¤inin kendi varsay─▒mlar─▒ ile tutars─▒z oldu─¤unu fark etmi┼¤lerdir, ama yine de Einstein kuantum mekani─¤inin sadece gizli de─¤i┼¤kenleriyle ba┼¤ka bir de─¤i┼¤iklik olmadan, kabul edilebilir bir teori elde etmeyi ama├¦lam─▒┼¤t─▒r. 1955 y─▒l─▒nda, hayat─▒n─▒n sonuna kadar olan yirmi y─▒lda bu fikirleri izlemi┼¤tir.
Aksine, 1964 y─▒l─▒nda yay─▒nlad─▒─¤─▒ k├ó─¤─▒tta John Bell, kuantum mekani─¤inin ve Einstein'─▒n tercih etti─¤i belirli ba─¤─▒nt─▒larda 3Ōüä2lik katsay─▒ya sahip gizli de─¤i┼¤ken teorisinin de─¤i┼¤ik deney sonu├¦lar─▒na ├Čnderlik edebilece─¤ini g├Čstermi┼¤tir.
Alain Aspect'in ve di─¤erlerinin yapt─▒─¤─▒ bir├¦ok Bell test deneyi bulunmaktad─▒r. Bunlar kuantum mekani─¤inin tahminlerinden ziyade, Einstein taraf─▒ndan desteklenen gizli de─¤i┼¤ken kuramlar─▒ s─▒n─▒f─▒n─▒ desteklemektedirler.
Kuantum mekani─¤i i├¦in olan imalar
├ćo─¤u fizik├¦i g├╝n├╝m├╝zde kuantum mekani─¤inin do─¤ru oldu─¤una ve EPR paradoksunun klasik sezgilerin fiziksel ger├¦ekli─¤e kar┼¤─▒l─▒k gelmemesinden dolay─▒ sadece bir "paradoks" oldu─¤una inanmaktad─▒r. EPR'nin yerellik konusunu nas─▒l yorumland─▒─¤─▒ kuantum mekani─¤inin kullan─▒mlar─▒n─▒n yorumlar─▒na ba─¤l─▒d─▒r. Kopenhag yorumuna g├Čre, genellikle ani dalga fonksiyonu ├¦├Čk├╝┼¤├╝n├╝n meydana geldi─¤i anla┼¤─▒lmaktad─▒r. Ancak, Kopenhag g├Čr├╝┼¤├╝nde, nedensel anl─▒k bir etkisi olmad─▒─¤─▒ ileri s├╝r├╝lm├╝┼¤t├╝r: Bu alternatif g├Čr├╝┼¤te, ├Čl├¦├╝mler sistemin kendisini de─¤il, fiziksel sistemdeki nicelikleri tan─▒mlamam─▒z─▒ etkiler. Bir├¦ok d├╝nyan─▒n yorumlanmas─▒nda, bu t├╝r ├Čl├¦├╝mlerde i┼¤lemlerin etkileri sadece ├Čl├¦├╝len par├¦ac─▒─¤─▒n durumunu etkiledi─¤inden, yerellik kesinlikle korunmaktad─▒r. Ancak, ├Čl├¦├╝m sonu├¦lar─▒ e┼¤siz de─¤ildir, her t├╝rl├╝ sonu├¦ elde edilebilir.
EPR paradoksu, ├Čl├¦├╝m s├╝recinin temelde klasik olmayan ├Čzelliklerini a├¦arak kuantum mekani─¤ine olan anlay─▒┼¤─▒m─▒z─▒ derinle┼¤tirdi. EPR ka─¤─▒d─▒n─▒n yay─▒nlanmas─▒ndan ├Čnce, bir ├Čl├¦├╝m genellikle ├Čl├¦├╝len sistemin ├╝zerine do─¤rudan ├¦arpt─▒r─▒lan fiziksel bir rahats─▒zl─▒k olarak d├╝┼¤├╝n├╝lm├╝┼¤t├╝r. Bir elektronun konumunu ├Čl├¦erken ├╝zerinde bir ─▒┼¤─▒─¤─▒n yans─▒d─▒─¤─▒n─▒n hayal edilmesi ve elektronu rahats─▒z edip ve pozisyonuna ba─¤l─▒ olarak kuantum mekaniksel belirsizlikleri bulmak buna ├Črneklerdir. Kuantum mekani─¤inde hala pop├╝ler olan bu tip a├¦─▒klamalar, ├Čl├¦├╝m├╝n par├¦ac─▒─¤─▒ direkt olarak rahats─▒z etmeden yap─▒lmas─▒ gerekti─¤ini g├Čsteren EPR paradoksu taraf─▒ndan ├¦├╝r├╝t├╝lm├╝┼¤t├╝r. Asl─▒nda, Yagil Aharonov ve ortaklar─▒ Weak ├Čl├¦├╝mleri olarak adland─▒r─▒lan bir teori geli┼¤tirdiler.
Kuantum dolanmas─▒na dayanan teknolojiler g├╝n├╝m├╝zde geli┼¤mektedirler. Kuantum ┼¤ifrelemesinde, dola┼¤─▒k par├¦ac─▒klar iz b─▒rakmadan ve dinlenilmeden sinyallerin iletilmesinde kullan─▒lmaktad─▒r. Kuantum hesaplamas─▒nda, dola┼¤─▒k kuantum durumu, klasik bilgisayarlardan daha h─▒zl─▒ i┼¤lem yapabilen paralel hesaplamalar─▒n yap─▒lmas─▒nda kullan─▒l─▒r.
Matematiksel denklemlendirim
Yukar─▒daki tart─▒┼¤ma, f─▒r─▒l─▒n kuantum mekaniksel denklemlendiriminin matematiksel yaz─▒l─▒m─▒ olarak ifade edilebilir. Bir elektron i├¦in spin serbestlik derecesi her kuantum durumu uzayda bir vekt├Čre denk gelen iki boyutlu karma┼¤─▒k uzay vekt├Čr├╝ olan V ile ili┼¤kilidir. x, y ve z y├Čn├╝nde f─▒r─▒la kar┼¤─▒l─▒k gelen i┼¤lemciler, s─▒ras─▒yla Sx, Sy ve Sz ┼¤eklinde g├Čsterilen, Pauli matrisleri kullan─▒larak yaz─▒labilir.
Bu denklemde 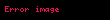
Sz 'nin ├Čzdurumu ┼¤u ┼¤ekilde g├Čsterilebilir;
ve Sx 'ninki;
Elektron-pozitron ├¦iftinin uzay vekt├Čr├╝ 
bu denklemde sa─¤ taraftaki iki terim daha ├Čnceden durum 1 ve durum 2 olarak tan─▒mlad─▒─¤─▒m─▒z niceliklerdir.
Yukar─▒daki denklemden f─▒r─▒l tekilinin ayr─▒ca ┼¤u ┼¤ekilde yaz─▒labilece─¤ini g├Črebiliriz;
yine sa─¤ taraftaki terimler durum 1a ve durum 2a olarak tan─▒mlad─▒─¤─▒m─▒z niceliklerdir.
Bunun nas─▒l yerel ger├¦ekli─¤i ihlal etti─¤ini anlamak i├¦in, Alice'in Sz veya Sx ├Čl├¦├╝m├╝nden sonra, Bob'un Sz veya Sx de─¤erinin tek olarak tan─▒mlanmas─▒d─▒r ve bu "fiziksel ger├¦ekli─¤in elementi"ne denk gelir. Bu, kuantum mekani─¤indeki ├Čl├¦├╝mlerin prensibiyle alakal─▒d─▒r. Sz de─¤eri ├Čl├¦├╝ld├╝─¤├╝nde, sistem durumu olan Žł Sz'in ├Čzvekt├Čr├╝nde ├¦├Čker. E─¤er ├Čl├¦├╝mlerin sonucu +z ise, ├Čl├¦├╝mden hemen sonra sistem durumu Žł'─▒n dikey ├¦─▒k─▒nt─▒s─▒na maruz kal─▒r ve ┼¤u formu al─▒r;
F─▒r─▒l tekili i├¦in yeni durum;
Ayn─▒ ┼¤ekilde, e─¤er Alice'in ├Čl├¦├╝m sonucu ŌłÆz ├¦─▒karsa, sistem dikey ├¦─▒k─▒nt─▒ya maruz kal─▒r;
bu, yeni durumun a┼¤a─¤─▒daki gibi oldu─¤unu g├Čsterir;
Bu, Sz i├¦in yap─▒lan ├Čl├¦├╝mde Bob'un pozitronunun tan─▒mland─▒─¤─▒na ve ilk durumda ŌłÆz veya ikinci durumda +z oldu─¤u anlam─▒na gelir.
Sx ve Sz, kuantum mekani─¤inde kesin sonu├¦lara sahip olamaz. Aralar─▒ndan biri i┼¤lemcilerin de─¤i┼¤memesi unsurunu kullanabilir;
Heisenberg belirsizlik ilkesi ile birlikte;
Kaynak├¦a
- "EPR Paradox". 6 Kas─▒m 2015 tarihinde kayna─¤─▒ndan ar┼¤ivlendi. Eri┼¤im tarihi: 10 Haziran 2014.
wikipedia, wiki, viki, vikipedia, oku, kitap, k├╝t├╝phane, k├╝t├╝bhane, ara, ara bul, bul, her┼¤ey, ne arasan─▒z burada,hikayeler, makale, kitaplar, ├Č─¤ren, wiki, bilgi, tarih, yukle, izle, telefon i├¦in, turk, t├╝rk, t├╝rk├¦e, turkce, nas─▒l yap─▒l─▒r, ne demek, nas─▒l, yapmak, yap─▒l─▒r, indir, ├╝cretsiz, ├╝cretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, m├╝zik, ┼¤ark─▒, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
EPR paradoksu kuantum mekaniginin Kopenhag yorumuna karsi erken ve etkili bir elestiridir Albert Einstein ve arkadaslari ve Nathan Rosen topluca EPR olarak bilinen kuantum mekaniginin daha once fark edilmemis fakat belli sonuclara sahip olan kabul edilmis denklemlendirimini meydana cikaran bir dusunce deneyi hazirladilar ancak zamanla bu denklemlendirimler mantiksiz gorundu Aciklanan senaryo kuantum dolaniklik olarak bilinen bir olay iceriyordu Albert Einstein 1931 Kuantum mekanigine gore bazi kosullar altinda ortaklasa veya bireysel olan cift kuantum sistemleri cift sistemde gerceklesen deneylerin sonuclarinin olasiliklarini kodlayan tek bir dalganin isleviyle tanimlanabilir Asagida ele alinan EPR makalesi yazildiginda yapilan deneyler sonucu bir deneyin sonucunun bazen tek bir tahmini olmadigi biliniyordu Bu tip bir belirsizlik bir isik suzmesi yarim gumuslenmis bir aynanin uzerine dustugunde gorulebilir Isik suzmesinin yarisi yansirken diger yarisi gececektir Eger isik suzmesinin siddeti tek bir foton gecene kadar indirgenirse kuantum mekaniginde fotonun yansimasi veya gecisi tahmin edilemez Bu etkinin rutin aciklamasi o zamanlar Heisenberg in belirsizlik ilkesiyle saglanmisti Fiziksel nicelikler eslenik denilen ciftler halinde gelir Bu tur eslenik ciftlerinin ornekleri arasinda konumu ve farkli eksenler etrafinda olculen bir parcacigin ve bilesenlerinin devinirligi verilebilir Bir nicelik olculdugunde ve belirlendiginde birlesmis nicelikler belirsizlesir Heisenberg bunu olcumden kaynaklanan bir rahatsizlik olarak aciklamistir 1935 yilinda yazilmis EPR makalesi bu aciklamanin yetersiz oldugunu gostermeyi amaclamistir A ve B olarak adlandirilan iki dolasik parcacigi dikkate aldigimizda A parcaciginin niceliginin olculmesi B parcaciginin esleniginin niceliginin hicbir temas ve karisiklik olmadan belirsizlesmesine neden olur Temel fikir bir sistemin icindeki iki parcacigin kuantum durumlari her zaman ikisinin ortak durumundan ayrisamaz Bunun bra ket yazilimindaki bir ornegi su sekildedir F 12 00 11 displaystyle Phi rangle frac 1 sqrt 2 left 00 rangle 11 rangle right Heisenberg belirsizlik ilkesi bazen yerel olmayan denilen bir kuantum etkisinin klasik bir aciklamasinin saglanmasini cabaladi EPR ye gore bu durumun iki olasi aciklamasi vardi Parcaciklar arasinda ayrim olsa bile ya aralarinda bir etkilesim vardi ya da tum olasi olcumlerin sonuclari hakkinda bilgiler parcaciklarda mevcuttu EPR yazarlari ikinci aciklamayi bazi kodlanmis gizli degiskenlerden dolayi tercih etmislerdir Bir etki aninda bir uzaklik boyunca yayilan ilk aciklama gorelilik teorisi ile celismekteydi Daha sonra kuantum mekaniginin kuralciligindan dolayi tamamlanmamis oldugu sonucuna vardilar cunku bu tip gizli degiskenlere kuantum mekaniginde yer yoktur Bell teoremi sonuclarindaki ihlaller genellikle Einstein Poldolsky ve Rosen tarafindan da varsayilan Bell in teoreminin hipotezlerinin bizim dunyamizda gecerli olmamasindan anlasilmaktadir Konuyu ve konuyla ilgili deneyleri inceleyen Alain Aspect ve grubu gibi fizikcilerin cogu EPR ilk dikkat cektiginde kuantum teorisinin ongordugu gibi EPR nin tercih ettigi yerel gizli degisken teorisini Bell esitsizliklerini ihlal ettiginden oturu gecersiz kabul etti EPR gelisimlerinin tarihiBu konulari ilk ortaya koyan makale 1935 yilinda yayinlanan Fiziksel Gercekligin Kuantum Mekaniksel Tanimi Tam Olarak Dusunulebilir Mi dir Einstein kuantum mekanik bicimciligi acisindan olcumlerle yorumlanarak ortaya cikanlar disindaki nesnel fiziksel bir gercekligin var oldugu gorusunu protesto etmis kendi dusuncesine daha cok uyan nedensellik teorisi icin hayatinin sonuna kadar mucadele etmistir Ancak Einstein in olumunden sonra bir EPR kagidinda anlatilan andiran deneyler Fransiz bilim adamlari Lamehi Rachti ve Mittig tarafindan 1976 yilinda Saclay Nukleer Arastirma Merkezinde gerceklestirilmistir Bu deneyler yerel gercekcilik fikrinin yanlis oldugunu gostermistir Kuantum mekanigi ve yorumlanmasiYirminci yuzyilin basindan beri kuantum kurami dogru mezoskopik ve mikroskobik dunyanin fiziksel gercekligini aciklayan birden fazla tekrarlanabilir fizik deneylerinde basarili oldugunu kanitlamistir Kuantum mekanigi atomunlari tanimlayan ve bir olcum cihazinda gozlenen tayfi cizgileri aciklama amaci ile gelistirilmistir Yirminci yuzyilin baslarinda iddiali olmasina ragmen konuyla ilgili henuz ciddi bir meydan okuma yapilmamistir Kuantum olaylarinin felsefi yorumlamasi ancak baska bir meseledir kuantum mekaniginin matematiksel denklemlendirimini yorumlamanin nasil olacaginin sorusu farkli felsefi goruslerden insanlarin farkli cevaplar vermesini dogurmustur Kuantum teorisi ve kuantum mekanigi belirleyici bir sekilde tek olcum sonuclari vermemektedir Kopenhag yorumlamasi olarak bilinen kuantum mekanigi anlayisina gore olcumlerin dalga islevlerinin anlik cokmesine neden olmasi ozdurumdaki kuantum sistemini betimler Einstein 1927 Solvay Konferansinda bu cokmenin canlandirmasini yapmistir Deneyi ic yuzeyi algilanim ekranina sahip kuredeki kucuk bir delikten elektron tanimlamasiyla yapmistir Bu deneyde elektronlar kurenin ic yuzeyiyle yaygin olarak daginik bir sekilde temasta bulunmustur Ancak bu elektronlar dalga cephelerinin girdigi noktadan butun yonlere genislemesiyle aciklanabilir Gunluk yasamdan da anlasilacagi gibi bir dalga algilanim ekraninda genis bir bolge kaplar fakat elektronlarin tek noktalarda ekrana bir etkisi olacaktir ve sonunda kendi ozdes dalga fonksiyonlari tarafindan aciklanan olasiliklari dogrultusunda bir model olusturacaktir Einstein konumuna bagli olarak neden her elektronun dalgasinin on cephesinin coktugunu niye elektronlarin yuzey uzerindeki enerji gibi los olmasi yerine tek parlak pirildanimlar olarak gorunmesini ve neden tek bir elektronun herhangi bir nokta yerine sabit tek bir noktada bulundugunu sorar Elektronlarin davranisi butun olasi noktalara gonderilmis fakat biri disinda tum hepsini gecersiz kilan bazi sinyallerin izlenimini verir Diger bir deyisle tum noktalar haricinde tek bir nokta secilebilir Einstein in karsitligiEinstein Kopenhag yorumunun en onemli rakibi oldu Onun gorusune gore kuantum mekanigi tamamlanmamisti Bunu yorumlayan John von Neumann ve David Bohm gibi diger yazarlar orijinal kagit acikca iddia edilmemis rastgele yapilan olcum sonuclarindan gizli degiskenleri sorumlu tutmustur 1935 EPR makalesi felsefi tartismayi fiziksel bir tartismanin icine sikistirmistir Yazarlar bir olcumun sonucu olan verilmis ozgul bir deneyde olcum gerceklesmeden once gerceklik unsuru denilen bir seyin gercek dunyada var oldugunu iddia etmislerdir Yazarlar gercekligin bu unsurlarinin her uzayzamandaki belli bir noktaya ait oldugunu yani yerel oldugunu varsaymaktadir Her element sadece uzay zamanin yani gecmisin onun isik konisinin gerisinde bulunan olaylardan etkilenmistir Bu iddialar artik yerel gercekcilik olarak bilinen teskil dogasi hakkinda varsayimlar uzerine kurulmustur EPR makalesi sik sik Einstein in goruslerinin tam bir ifadesi olarak alinmis olsa da basta Einstein ve Rosen ile Gelismis Calisma Enstitusundeki gorusmelere dayanarak Podolsky tarafindan yazilmistir Einstein daha sonra Erwin Schrodinger e bu benim normalde istedigim gibi bir sonuc vermedi daha ziyade onemli sey tabiri caizse bicimcilik tarafindan boguldu demistir 1936 yilinda Einstein yerel gercekci fikirlerinin bir bireysel hesabini sundu Paradoksun tanimiOrijinal EPR paradoksu kuantum mekaniginin bir tahmini olan bir kuantum parcaciginin konumunun ve devinirliginin ayni anda bilinememesine meydan okur Bu meydan okuma baska fiziksel ozelliklerin diger ciftlerinin genislemesiyle olabilir EPR Makalesi Orijinal makale etkilesime gecmesine izin verilen iki sisteme ne olacagini ve bir sure sonra etkilesim kalmadiginda neler olacagini tanimlama amaci gutmustur Kumar in sozleriyle bu A ve B olan iki parcacigin kisaca etkilesimde olmasi ve daha sonra farkli yonlere hareket etmesi olarak tanimlanabilir Heisenberg in belirsizlik ilkesine gore devinirligi ve B parcaciginin tam olarak konumunu ayni anda olcmek mumkun degildir fakat Kumar a gore A parcaciginin kesin konumunu belirlemek mumkundur Bu nedenle olcumler sonucu A nin bilinen kesin konumu yardimiyla B nin kesin konumu bulunabilir Ayrica A parcaciginin devinirligi olculebildiginden B parcacigininkini de A ya bagli olarak bulmak mumkundur Kumar bunu su sekilde yazmistir EPR B parcacigi es zamanli olarak kesin ve gercek bir devinirlik ve konum degerine sahiptir yargisini kanitlamis ve savunmustur EPR B parcacigi fiziksel olarak rahatsiz olma olasiligi olmadan parcacik A uzerinde yapilan olcumler sonucunda B nin ya devinirliginin ya da pozisyonunun kesin degerlerini bulmayi amacladi EPR Kuantum Mekanigi gercek uygulama araligini sorgulamak icin bir paradoks yaratmaya calisti Bu paradoks Kuantum teorisi iki degerin de parcacik icin tahmin edilemez olmasini ve henuz EPR dusunce deneyinin hepsinin belirli degerlere sahip olmasi gerektigini gostermesini iceriyordu EPR kagidi Biz fiziksel gercekligin kuantum mekaniksel taniminin tam olarak dalga islevleri tarafindan aciklanamayacagi sonunu kabul etmek zorunda kaliyoruz demistir EPR kagidi su soz ile sonlanir Biz boylece dalga fonksiyonun fiziksel gercekligin tam bir aciklamasini yapamadigini gostersek de biz boyle bir aciklamanin var olup olmadigi sorusuna kesin bir cevap bulamadik Biz boyle bir teori mumkun olduguna yine de inaniyoruz Dolasik durumda olcumler Elimizde elektron pozitron ciftlerini yayan bir kaynak var ve Alice adindan bir gozlemcinin oldugu A noktasina elektron Bob adinda bir gozlemci bulunan B noktasina da pozitron gonderiyoruz Kuantum mekanigine gore kaynagimizi yayilan her ciftin tekli firil adi verilen kuantum durumunu isgal edecegi sekilde ayarlayabiliriz Boylece bu parcaciklar dolasiktir diyebiliriz Bu durum 1 ve durum 2 olarak adlandirdigimiz iki kuantum cakismasi durumu olarak gorulebilir Durum 1de pozitif z ekseninde bir firili olan elektron ve negatif z ekseninde bir firila sahip pozitron vardir Durum 2de ise elektron negatif z ekseninde bir firila sahipken pozitif z ekseninde pozitron bir firila sahiptir Bundan dolayi olcum yapmadan tekli firil durumundaki bir parcacigin durum firilini belirlemek mumkun degildir Elektron pozitron ciftiyle yapilan EPR dusunce deneyi Merkezdeki kaynak iki gozlemciye parcacik gonderir sol taraftaki Alice gozlemcisine elektron gonderirken sag taraftaki Bob gozlemcisine pozitron gonderilir ve firil olcumleri yapilabilir Artik Alice z ekseni etrafindaki firili olcer ve z veya z olmak uzere iki muhtemel sonuc elde edebilir Eger elde ettigi sonuc z ise kuantum mekaniginin Kopenhag yorumlamasina gore sistemin kuantum durumu durum 1de coker Kuantum durumu sistemde gerceklesen her turlu olcumun sonucunu belirler Bu durumda eger Bob z ekseni etrafinda sonradan olcum yaparsa bulacagi sonuc z ekseninde olur Ayni sekilde eger Alice z ekseninde sonuc alirsa Bob z ekseninde bir sonuc alir Ozellikle z eksenini secmemizin belirli bir nedeni yoktur kuantum mekanigine gore tekli firil durumu x eksenini gosteren firil durumunun cakismasi da esit olur Eger Alice ve Bob firili x ekseninde olcmeye karar verirse buna durum 1a ve durum 2a deriz Durum 1a da Alice in elektronu x firilina sahipken Bob un pozitronu x firilina sahiptir Durum 2a da ise Alice in elektronu x firilina sahipken Bob un pozitronu x firilina sahiptir Bundan dolayi Eger Alice x olcerse sistem durum 1ada coker ve Bob x sonucunu elde eder Eger Alice x olcerse sistem durum 2a da coker ve Bob x sonucunu elde eder Herhangi bir eksende firillari olculurse sonuc her zaman birbirlerinin tersi olur Bu durum sadece parcaciklar birbirlerine bagliysa aciklanabilir Ya her eksende kesin olarak farkli firila sahip sekilde yaratilmislardir gizli degisken tartismasi ya da birbirlerine baglilardir ve bu yuzden bir elektron digerinin eksenin hangi tarafinda oldugunu hissediyordur ve onun karsit sonucunu aliyorudur dolasiklik tartismasi Ayrica eger iki parcacigin farkli eksenler boyunca firillari olculuyorsa x ekseninde elektron firili olculdugunde ve x eksenindeki pozitronun firili yok sayildiginda z eksenindeki pozitronun firili kesin degildir cunku olcum yerini almistir ve zaten ikinci bir eksende firili mevcuttur Buna ragmen deneyler tarafindan onaylanan kuantum mekanigi hakkindaki varsayimlar herhangi bir gizli degisken teorisiyle aciklanamaz Bu Bell teoreminde gosterilmistir Kuantum mekaniginde Heisenberg belirsizlik ilkesine gore iki degisken icin de kuantum durumu kesin bir sonuca sahip olamaz ve bu durum x firili ve z firili uyumsuz gozlemlenenlerdir anlamina gelir Alice in z firili olctugunu varsayalim ve buldugu sonuc z olsun bu durumda kuantum durumu durum 1de coker Simdi z firilini olcmek yerine Bob x firilini olcsun Kuantum mekanigine gore eger sistem durum 1de ise Bob un x firil olcumu 50 ihtimalle xde olabilir ya da 50 ihtimalle xde olabilir Bob un kendisi olcum yapana kadar nasil bir sonuc elde edilecegini tahmin etmek imkansizdir Bu konunun donum noktasidir Bob pozitronun x firilini olctugunde kesin bir sonuca ulasabilir cunku kendi parcacigini rahatsiz etmemistir Bob un pozitronu 50 ihtimalle x veya x dedir ve kesin bir sonuc yoktur cunku Bob un pozitronu Alice in elektronunu bilir ve Alice in elektronu bilinip olculdugu icin Bob un elektronunun spini hakkinda kesin bir bilgi elde edemeyiz Kopenhag yorumuna gore dalga islevi olcum yapildigi zaman coker ve bu yuzden belli bir uzaklikta bir etki olmalidir veya pozitron bilmesi gerekenden daha fazlasini bilmelidir Paradoksun ozeti Ilk parcacigin fiziksel olcumleri kendi konumunda devinirlige etkisi kesin degildir fakat ilk parcacigin devinirligini olcmek oburunun konumunun kesinligini etkiler Einstein Podolsky ve Rosen ikinci parcacigin nasil kesin olmayan konumuna ragmen kesin bir devinirlige sahip oldugunu sorguladi Bir parcacik digeriyle uzayda iletisim halinde oldugundan bu bir paradokstur Bu arada Bell firili kendi orneginde kullandi fakat kuantum mekaniginde gozlemlenebilirler denilen bircok cesit fiziksel nicelik kullaniliyordu EPR kagidi bu gozlemlenebilirlerin devinirligi icin kullaniliyordu EPR planinin deneysel gerceklestirmeleri genellikle foton kutuplasmasinda kullaniyor cunku kutuplasmis fotonlarin hazirlanmasi ve olculmesi kolaydir EPR deneylerindeki yerellik Yerellik ilkesi bir yerde meydana gelen fiziksel islemlerin baska bir yerdeki gerceklik unsurlari uzerinde bir etkisinin olmamasi gerektigini belirtir Ilk bakista bu bilgiler nedenselligi ihlal etmeden isik hizindan daha hizli iletilmeyen bilgileri savunan ozel goreliligin sonuclari hakkinda makul bir varsayim gibi gorunuyordu Genellikle nedenselligi ihlal eden herhangi bir teori de icten tutarsiz olacagindan yararsiz olacagi dusunulmektedir Kuantum mekanigi ve klasik tanimlarin birlestirmek icin olan olagan kurallar nedensellik yasasini ihlal etmeden yerellik ilkesini ihlal etmektedir Nedensellik korunmaktadir cunku Alice in Bob un olcum eksenini yonlendirerek mesaj iletmesinin baska bir yolu yoktur Alice hangi ekseni kullanirsa kullansin 50 oraninda veya sonuc elde etme olasiligi vardir ve kuantum mekanigine gore temel olarak hangi sonucu alacagini etkilemesi imkansizdir Ayrica Bob sadece bir kez kendi olcumunu yapabilir cunku kuantum mekaniginin temel ozelligi aldigi elektronlarin milyon tane kopyasini yapmasini hepsine tek tek firil olcumu yapmasini ve sonuclarin istatistiksel dagilimina bakmasini imkansiz kilar Bu nedenle eger sadece bir olcum yapmasina izin verilirse veya sonuc bulmasi Alice le ayni eksende olup olmamasina bagli olmadan 50 sansi oldugunu goruruz Yine de yerellik ilkesi fiziksel sezgilere guclu bir sekilde hitap etmistir ve Einstein Podolsky ve Rosen bu yuzden bu teoriyi terk etmek istemiyorlardi Einstein kuantum mekaniksel tahminlerle bir noktada urkutucu diyerek dalga gecmistir Bu nedenle kuantum mekaniginin henuz tamamlanmamis olmasiyla sonuclandirmislardir Son yillarda ise EPR nin ulastigi sonuc yerellik anlamadaki gelismelerden ve kuantumun elverisli olmamasindan suphe uyandirmistir Yerellik kelimesi fizikte bircok anlama sahiptir Ornegin kuantum alan teorisinde yerellik uzayin degisik noktalarindaki kuantum alanlarinin birbirleriyle etkilesimde olmamalari anlamina gelir Ancak bu anlamda yerel olan kuantum alan teorileri EPR tarafindan tanimlanan yerellik ilkesine aykiri gorunmektedir ama yine de daha genel anlamda yerelligi ihlal etmezler Dalga islevinin cokusu kuantum elverissizliginin epifenomeni olarak gorulebilir Temel davranis yerel nedenselligi ihlal etmediginden bu gercek ya da belirgin olsun dalga fonksiyonu cokusu ek bir etki yapar Yukaridaki ornekte belirtilen nedenle ne EPR deneyinim ne de herhangi bir kuantum deneyinin gosterilmesinin isik sinyalinden hizli olmasi mumkun degildir Paradoksun cozumuGizli degiskenler EPR paradoksunu cozmek icin cesitli yollar vardir EPR tarafindan onerilen bir tanesi kuantum mekanigidir deneysel senaryolarda cesitli basarilar elde etmesine ragmen aslinda tamamlanmamis bir teoridir Diger bir deyisle kuantum mekanigi bir derece basarili bir de olsa istatistiksel yaklasim gibi davranan doganin henuz kesfedilmemis bazi teorileri vardir Kuantum mekaniginin aksine daha tam bir teori tum gerceklik unsurlarina karsilik gelen degiskenleri icerebilir Heisenberg belirsizlik ilkesi yani iletmez kuantum gozlenebilirlerinin gozlenen etkilerine yol vermek icin bu degiskenler uzerinde hareket eden bazi bilinmeyen mekanizmalar olmalidir Boyle bir teoriye gizli degisken teorisi denir Bu fikir gostermek icin yukaridaki dusunce deneyi icin cok basit bir gizli degisken teorisini hazirlayabiliriz Bir kaynaktan yayilan kuantum tekli firil durumu dogru fiziksel durum icin x firili ve z firilinin kesin degeri icin yaklasik bir tanim olusturur Bu gercek durumlarda Bob a giden pozitron her zaman Alice e giden elektronun ters firil degerine sahip olacaktir ancak aksi bir durumda degerler tamamen rastgele olacaktir Ornegin kaynak tarafindan yayilan ilk cift Alice e z x ve Bob a z x olabilir bir sonraki cift ise Alice e z x ve Bob a z x ve benzerleri olabilir Bu nedenle Bob un olcme ekseni Alice inki ile ayni hizada ise Bob mutlaka Alice ne gelirse tersini alacak aksi halde Bob esit olasilikla veya alicaktir Olcumlerimizi z ve x eksenleriyle sinirladigimizi varsayarsak boyle bir gizli degisken teorisi kuantum mekaniginden deneysel olarak ayirt edilemez Gercekte Alice ve Bob un kendi olcumlerini yaptigi sonsuz sayida eksen olabilir bu yuzden sonsuz sayida bagimsiz gizli degiskenler olmasi gerekir Ancak bu ciddi bir sorun degildir cunku biz gizli degisken teorisini cok basit bir sekilde bagintisal yazdik ve daha sofistike bir teorinin bu konuda yama yapmasi mumkun olabilir Bu gizli degiskenlerin fikrinde cok daha ciddi bir sorun oldugunu ortaya cikiyor Bell esitsizlikleri 1964 yilinda EPR dusunce deneyindeki kuantum mekaniginin tahminlerinin gizli degisken teorileriyle yerel gizli degisken kuramlarinin onemli olcude farkli oldugunu gosterdi Kabaca soylemek gerekirse kuantum mekaniginin diger eksenlerde yapilan olcum sonuclarinin istatistiksel bagintisi gizli degisken teorilerindekinden daha gucludur Bu farkliliklar esitsizlik iliskilerini kullanan Bell esitsizlikleri olarak bilinen deneysel saptanabilen prensiplerdir Eberhard tarafindan daha sonraki calismalarda Bell in esitsizliklerine onculuk eden gizli degisken kuramlarinin yerelligi ve karsi olgusal kesinlik ozelligi gosterilmistir Bu ilkelerin gecerli oldugu herhangi bir teori esitsizlikleri uretir Arthur Fine sonradan esitsizlikleri tatmin eden herhangi bir teorinin yerel gizli degisken teorisi ile modellenebilir oldugunu gostermistir Bell in kagit yayinlanmasindan sonra Bell esitsizliklerini test etmek icin cesitli deneyler icat edildi Bunlar genellikle foton kutuplasmasi olcumlerine dayaniyordu Bugune kadar yapilan tum deneylerin standart kuantum mekanigi teorisinin ongoruleri dogrultusunda oldugu bulunmustur Ancak Bell in teoremi tum olasi felsefi olarak realist olan teoriler icin gecerli degildir Kuantum mekaniginin felsefi gercekciligin tum kavramlari ile tutarsiz olmasi yaygin bir yanilgidir Kuantum mekaniginin realistik yorumlamasi mumkundur fakat yukarida tartisildigi gibi bu tip yorumlamalar yerelligi ya da karsi olgusal kesinligi reddeder Ana fizik karsi olgusal kesinligi reddeden gercekcilik kavramini korumak icin ugras verirken yerelligi tutmayi da tercih eder Boyle genel realist yorumlarin ornekleri tutarli gecmislerini yorumlanmasi ve ilk kez 1986 yilinda John G Cramer tarafindan onerilen islem yorumudur Fine in calismalari gosterdi ki yerelligi alarak iki istatistiksel degisken olan karsi olgusal kesinlikler tutarsiz bir sekilde iliskilidir ve bu tur senaryolar olmasina ragmen daha gizemli senaryolarin verilmesi ile tutarsizlik karsi olgusal kesinlik sezgilerde gorunebilir Yerelligin ihlalin ozel gorelilik ile bagdastirmak zordur ve nedensellik ilkesi ile uyumsuz oldugu dusunulmektedir Ancak Schrodinger denkleminin sartlarini biri olarak tanimlanan kuantum potansiyeli seklinde bir varsayimi yerel olmayan mekanizmasi tanitilirken kuantum mekaniginin Bohm yorumlanmasi karsi olgusal kesinlikce tutarlidir Bazi bu alanda calisanlar gercek deneylerde kacamaklari somuren gizli degisken teorisini bagintisal olarak yazmayi denemistir Ayrica yerel gizli degiskenleri olmayan bireysel EPR benzeri deneylerin aciklamasi da vardir Ornekler David Bohm ve Lucien Hardy tarafindan onerilebilir Einstein in saf cebirsel teoriye inanci Kuantum mekaniginin Bohm yorumlanmasina gore evrenin durumunun kuantum dalga islevleri cokmeden zaman icinde sorunsuzca gelistigi varsayilmaktadir Kopenhag yorumlanmasi icin olusan sorunlardan biri dalga islevinin cokusunun tanimlanmasidir Einstein kuantum mekaniginin fiziksel olarak eksik ve mantiksal olarak yetersiz oldugunu ileri surmustur Goreliligin Anlami nda Einstein Birisi neden gercekligi surekli bir alanda aciklanamayacagina iyi bir neden versin demistir Kuantum olaylarina bakildiginda sonlu bir enerjinin sonlu bir sistemi tamamen kuantum numaralari denilen sonlu bir dizi rakamla tarif edilebilir Bu bir sureklilik teorisi icin uygun olarak gorulmemektedir ve gercekligin temsili icin bir cebirsel teori bulma girisimine neden olmaktadir Ama hic kimse bu tip bir teori icin bir temel bulamamistir Eger zaman mekan ve enerji Planck olceginde alt tabakadan turetilmis ikincil ozellikleri ise Bell in teoremi hala gecerli olsa da Einstein in varsayimsal cebirsel sistemi EPR paradoksunu cozmek icin yeterli olabilir Fredkin in Sonlu Doga Hipotezi nde Edward Fredkin Einstein in varsayimsal cebirsel sistemi icin bir bilgi temeli onerdi Eger fiziksel gerceklik tamamen sonlu ise Kopenhag yorumu Planck olceginde bir bilgi islem sistemine bir yaklasim olabilir Kabul edilebilir teoriler ve deneyler Durumun bugunku gorusune gore kuantum mekanigi kesin bir dille kabul edilebilir herhangi bir fiziksel teorinin yerel gercekciligi yerine getirmesi gerektigini savunan Einstein in yerel felsefi onermesiyle celismektedir 1935 yilinda yazilan EPR kagidinda yazarlar kuantum mekaniginin kendi varsayimlari ile tutarsiz oldugunu fark etmislerdir ama yine de Einstein kuantum mekaniginin sadece gizli degiskenleriyle baska bir degisiklik olmadan kabul edilebilir bir teori elde etmeyi amaclamistir 1955 yilinda hayatinin sonuna kadar olan yirmi yilda bu fikirleri izlemistir Aksine 1964 yilinda yayinladigi kagitta John Bell kuantum mekaniginin ve Einstein in tercih ettigi belirli bagintilarda 3 2 lik katsayiya sahip gizli degisken teorisinin degisik deney sonuclarina onderlik edebilecegini gostermistir Alain Aspect in ve digerlerinin yaptigi bircok Bell test deneyi bulunmaktadir Bunlar kuantum mekaniginin tahminlerinden ziyade Einstein tarafindan desteklenen gizli degisken kuramlari sinifini desteklemektedirler Kuantum mekanigi icin olan imalar Cogu fizikci gunumuzde kuantum mekaniginin dogru olduguna ve EPR paradoksunun klasik sezgilerin fiziksel gerceklige karsilik gelmemesinden dolayi sadece bir paradoks olduguna inanmaktadir EPR nin yerellik konusunu nasil yorumlandigi kuantum mekaniginin kullanimlarinin yorumlarina baglidir Kopenhag yorumuna gore genellikle ani dalga fonksiyonu cokusunun meydana geldigi anlasilmaktadir Ancak Kopenhag gorusunde nedensel anlik bir etkisi olmadigi ileri surulmustur Bu alternatif goruste olcumler sistemin kendisini degil fiziksel sistemdeki nicelikleri tanimlamamizi etkiler Bircok dunyanin yorumlanmasinda bu tur olcumlerde islemlerin etkileri sadece olculen parcacigin durumunu etkilediginden yerellik kesinlikle korunmaktadir Ancak olcum sonuclari essiz degildir her turlu sonuc elde edilebilir EPR paradoksu olcum surecinin temelde klasik olmayan ozelliklerini acarak kuantum mekanigine olan anlayisimizi derinlestirdi EPR kagidinin yayinlanmasindan once bir olcum genellikle olculen sistemin uzerine dogrudan carptirilan fiziksel bir rahatsizlik olarak dusunulmustur Bir elektronun konumunu olcerken uzerinde bir isigin yansidiginin hayal edilmesi ve elektronu rahatsiz edip ve pozisyonuna bagli olarak kuantum mekaniksel belirsizlikleri bulmak buna orneklerdir Kuantum mekaniginde hala populer olan bu tip aciklamalar olcumun parcacigi direkt olarak rahatsiz etmeden yapilmasi gerektigini gosteren EPR paradoksu tarafindan curutulmustur Aslinda Yagil Aharonov ve ortaklari Weak olcumleri olarak adlandirilan bir teori gelistirdiler Kuantum dolanmasina dayanan teknolojiler gunumuzde gelismektedirler Kuantum sifrelemesinde dolasik parcaciklar iz birakmadan ve dinlenilmeden sinyallerin iletilmesinde kullanilmaktadir Kuantum hesaplamasinda dolasik kuantum durumu klasik bilgisayarlardan daha hizli islem yapabilen paralel hesaplamalarin yapilmasinda kullanilir Matematiksel denklemlendirimYukaridaki tartisma firilin kuantum mekaniksel denklemlendiriminin matematiksel yazilimi olarak ifade edilebilir Bir elektron icin spin serbestlik derecesi her kuantum durumu uzayda bir vektore denk gelen iki boyutlu karmasik uzay vektoru olan V ile iliskilidir x y ve z yonunde firila karsilik gelen islemciler sirasiyla Sx Sy ve Sz seklinde gosterilen Pauli matrisleri kullanilarak yazilabilir Sx ŌäÅ2 0110 Sy ŌäÅ2 0 ii0 Sz ŌäÅ2 100 1 displaystyle S x frac hbar 2 begin bmatrix 0 amp 1 1 amp 0 end bmatrix quad S y frac hbar 2 begin bmatrix 0 amp i i amp 0 end bmatrix quad S z frac hbar 2 begin bmatrix 1 amp 0 0 amp 1 end bmatrix Bu denklemde ŌäÅ displaystyle hbar indirgenmis Planck sabitidir ya da 2p ye bolunmus Planck sabiti Sz nin ozdurumu su sekilde gosterilebilir z 10 z 01 displaystyle left z right rangle leftrightarrow begin bmatrix 1 0 end bmatrix quad left z right rangle leftrightarrow begin bmatrix 0 1 end bmatrix ve Sx ninki x 12 11 x 12 1 1 displaystyle left x right rangle leftrightarrow frac 1 sqrt 2 begin bmatrix 1 1 end bmatrix quad left x right rangle leftrightarrow frac 1 sqrt 2 begin bmatrix 1 1 end bmatrix Elektron pozitron ciftinin uzay vektoru V V displaystyle V otimes V dur elektronun ve pozitronun uzay vektorunun tansor carpimi Firil tekil durumu ps 12 z z z z displaystyle left psi right rangle frac 1 sqrt 2 bigg left z right rangle otimes left z right rangle left z right rangle otimes left z right rangle bigg bu denklemde sag taraftaki iki terim daha onceden durum 1 ve durum 2 olarak tanimladigimiz niceliklerdir Yukaridaki denklemden firil tekilinin ayrica su sekilde yazilabilecegini gorebiliriz ps 12 x x x x displaystyle left psi right rangle frac 1 sqrt 2 bigg left x right rangle otimes left x right rangle left x right rangle otimes left x right rangle bigg yine sag taraftaki terimler durum 1a ve durum 2a olarak tanimladigimiz niceliklerdir Bunun nasil yerel gercekligi ihlal ettigini anlamak icin Alice in Sz veya Sx olcumunden sonra Bob un Sz veya Sx degerinin tek olarak tanimlanmasidir ve bu fiziksel gercekligin elementi ne denk gelir Bu kuantum mekanigindeki olcumlerin prensibiyle alakalidir Sz degeri olculdugunde sistem durumu olan ps Sz in ozvektorunde coker Eger olcumlerin sonucu z ise olcumden hemen sonra sistem durumu ps in dikey cikintisina maruz kalir ve su formu alir z ŽĢ ŽĢ V displaystyle left z right rangle otimes left phi right rangle quad phi in V Firil tekili icin yeni durum z z displaystyle left z right rangle otimes left z right rangle Ayni sekilde eger Alice in olcum sonucu z cikarsa sistem dikey cikintiya maruz kalir z ŽĢ ŽĢ V displaystyle left z right rangle otimes left phi right rangle quad phi in V bu yeni durumun asagidaki gibi oldugunu gosterir z z displaystyle left z right rangle otimes left z right rangle Bu Sz icin yapilan olcumde Bob un pozitronunun tanimlandigina ve ilk durumda z veya ikinci durumda z oldugu anlamina gelir Sx ve Sz kuantum mekaniginde kesin sonuclara sahip olamaz Aralarindan biri islemcilerin degismemesi unsurunu kullanabilir Sx Sz iŌäÅSy 0 displaystyle left S x S z right i hbar S y neq 0 Heisenberg belirsizlik ilkesi ile birlikte DSx2 DSz2 14 Sx Sz 2 displaystyle left langle Delta S x 2 right rangle left langle Delta S z 2 right rangle geq frac 1 4 left left langle left S x S z right right rangle right 2 Kaynakca Einstein A Podolsky B Rosen N 15 Mayis 1935 Can Quantum Mechanical Description of Physical Reality Be Considered Complete Physical Review 47 10 777 780 doi 10 1103 PhysRev 47 777 12 Mayis 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 6 Ekim 2022 EPR Paradox 6 Kasim 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 10 Haziran 2014
 Azərbaycanca
Az╔Örbaycanca ąæąĄą╗ą░čĆčāčüą║č¢
ąæąĄą╗ą░čĆčāčüą║č¢ Dansk
Dansk Deutsch
Deutsch Espa├▒ola
Espa├▒ola Fran├¦ais
Fran├¦ais Indonesia
Indonesia Italiana
Italiana µŚźµ£¼Ķ¬×
µŚźµ£¼Ķ¬× ęÜą░ąĘą░ęø
ęÜą░ąĘą░ęø Lietuvos
Lietuvos Nederlands
Nederlands Português
Portugu├¬s ąĀčāčüčüą║ąĖą╣
ąĀčāčüčüą║ąĖą╣ ÓĘāÓĘÆÓČéÓĘäÓČĮ
ÓĘāÓĘÆÓČéÓĘäÓČĮ Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó
Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó T├╝rk├¦e
T├╝rk├¦e ąŻą║čĆą░茹Įčüčīą║ą░
ąŻą║čĆą░茹Įčüčīą║ą░ õĖŁÕ£ŗõ║║
õĖŁÕ£ŗõ║║ United State
United State Afrikaans
Afrikaans