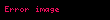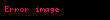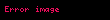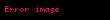Sayılar teorisinde, Skewes' sayısı, birkaç çok büyük sayıdan biridir. Güney Afrikalı matematikçi tarafından bulunan ve en küçük x doğal sayılarının belirleyen şöyle bir ifadedir:
buradaki π(x), ve li(x) ise . Bu sınırlar geliştirildi: bir geçiş noktasıdır.
Skewes sayıları
Skewes'ın öğretmeni olan John Edensor Littlewood, 1914'te 'da, büyük bir sayı olduğunu ve π(x) − li(x) fark işaretinin son derece sık değişdiğini kanıtladı. Sonradan tüm sayısal deliller, π(x)'nin daima li(x)'den daha az olduğunu gösterdi.
1933'te Skewes, Riemann hipotezinin doğruluğunu ve x gibi bir sayının π(x) < li(x)'i ihlal ettiğini aşağıdaki şekilde ispatladı;
1955'te Skewes, Riemann hipotezini varsaymaksızın. x gibi bir değerin olduğunu şöyle ispatladı;
Her iki Skewes sayıları, matematiksel delillerdeki çoğu büyük sayılarla karşılaştırıldığında onlardan büyüktür ve neredeyse Graham sayısı kadardır.
Son tahminler
Bu devasa üst sınırlar, Rieman zeta fonksiyonunun sıfırlarıyla büyük ölçekli bilgisayar hesaplamalarını kullanarak epeyce azaltıldı. Keşisme noktasının geçerli değerini için ilk yaklaşım 1966'da Lehman tarafından yapıldı. Lehman, 1,53×101165 ile 1,65×101165 arasında, 10500 ardışık x tam sayıları olduğunu π(x) > li(x) ile gösterdi. Riemann hipotezini kullanmadan Herman te Riele, 2000 yılında 7×10370 şeklinde bir üst sınır olduğunu ispatladı.
Riemann formülü
Riemann, π(x) için şöyle bir formül geliştirdi;
buradaki toplama, Rieman zeta fonksiyonunun ρ sıfırlarından fazladır. π(x) = li(x) (eğer Riemann hipotezi doğruysa) En büyük hata terimi yaklaşımındaki en büyük hata terimi 
Rieman hipotezinin yanlış olduğu varsayılırsa, argüman çok basit olur. li(xρ) terimlerinden dolayı, sıfırlal ihlal edilirse, Riemann hipotezi (gerçek bölüm 1/2'den daha büyüktür), nihayet li(x1/2)'den büyük olur.
Dış bağlantılar
- Demichel, Patrick (2005), Asal hesaplama fonksiyonu ve ilgili konular (PDF), 3.1415, Google, erişim tarihi: 4 Kasım 2007[] π(x) − li(x) farkının birçok grafiklerini içeriyor.
Patrick Demichel. Asal hesaplama fonksiyonu ve ilgili konular. 20.09.2009'da gözden geçirildi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Sayilar teorisinde Skewes sayisi birkac cok buyuk sayidan biridir Guney Afrikali matematikci tarafindan bulunan ve en kucuk x dogal sayilarinin belirleyen soyle bir ifadedir p x gt li x displaystyle pi x gt operatorname li x buradaki p x ve li x ise Bu sinirlar gelistirildi e727 952 displaystyle e 727 952 bir gecis noktasidir Skewes sayilariSkewes in ogretmeni olan John Edensor Littlewood 1914 te da buyuk bir sayi oldugunu ve p x li x fark isaretinin son derece sik degisdigini kanitladi Sonradan tum sayisal deliller p x nin daima li x den daha az oldugunu gosterdi 1933 te Skewes Riemann hipotezinin dogrulugunu ve x gibi bir sayinin p x lt li x i ihlal ettigini asagidaki sekilde ispatladi eee79 lt 10101034 displaystyle e e e 79 lt 10 10 10 34 1955 te Skewes Riemann hipotezini varsaymaksizin x gibi bir degerin oldugunu soyle ispatladi 101010963 displaystyle 10 10 10 963 Her iki Skewes sayilari matematiksel delillerdeki cogu buyuk sayilarla karsilastirildiginda onlardan buyuktur ve neredeyse Graham sayisi kadardir Son tahminlerBu devasa ust sinirlar Rieman zeta fonksiyonunun sifirlariyla buyuk olcekli bilgisayar hesaplamalarini kullanarak epeyce azaltildi Kesisme noktasinin gecerli degerini icin ilk yaklasim 1966 da Lehman tarafindan yapildi Lehman 1 53 101165 ile 1 65 101165 arasinda 10500 ardisik x tam sayilari oldugunu p x gt li x ile gosterdi Riemann hipotezini kullanmadan Herman te Riele 2000 yilinda 7 10370 seklinde bir ust sinir oldugunu ispatladi Riemann formuluRiemann p x icin soyle bir formul gelistirdi p x li x li x 2 rli xr ufak terimler displaystyle pi x operatorname li x frac operatorname li sqrt x 2 sum rho operatorname li x rho text ufak terimler buradaki toplama Rieman zeta fonksiyonunun r sifirlarindan fazladir p x li x eger Riemann hipotezi dogruysa En buyuk hata terimi yaklasimindaki en buyuk hata terimi li x 2 displaystyle operatorname li sqrt x 2 dir li x genellikle p x den daha buyuktur Yukaridaki diger terimler biraz daha kucuktur Rieman hipotezinin yanlis oldugu varsayilirsa arguman cok basit olur li xr terimlerinden dolayi sifirlal ihlal edilirse Riemann hipotezi gercek bolum 1 2 den daha buyuktur nihayet li x1 2 den buyuk olur Dis baglantilarDemichel Patrick 2005 Asal hesaplama fonksiyonu ve ilgili konular PDF 3 1415 Google erisim tarihi 4 Kasim 2007 olu kirik baglanti p x li x farkinin bircok grafiklerini iceriyor Patrick Demichel Asal hesaplama fonksiyonu ve ilgili konular 20 09 2009 da gozden gecirildi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans