Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Kontrol diyagramı, bir kalite izleme diyagramıdır. Doğada, toplumda ve insan etkisi ile meydana gelen tüm olaylarda değişkenlik bilinen bir olgudur. Bu nedenle üretim sürecinde çeşitli nedenlerin etkisi sonucu değişkenliğin ortaya çıkması, doğal ve kaçınılmaz kabul edilmektedir. Aslında kalite kontrol faaliyetlerinin temel amacı, üretim sürecinin ekonomik olması koşulu ile kontrol altında tutulmasıdır. Buradaki ekonomiklik ile ifade edilmek istenen husus, kontrolün gerçekleştirilmesi için harcanan çabalarla elde edilen yararlar arasında bir dengenin sağlanmasıdır.
Bu aşamada kontrol için kullanılan diyagramların tanımına gelirsek ; proses kontrolünün istatistik yöntemlerle ekonomik ve güvenilir biçimde gerçekleştirilebilmesinde kullanılan başlıca araç kontrol diygramlarıdır. Armand V. Feigenbaum, kontrol diyagramını; mamulun, mamulü oluşturan parçaların veya diğer bileşenlerin kalite spesifikasyonlarını geçmiş deneyimlere dayanarak saptanan limitlere göre kronolojik olarak karşılaştırmaya yarayan grafik araç olarak tanımlamaktadır.
Türleri
Kabul kontrol diyagramları
Belirli bir boyut için mühendislik toleransı, imalat prosesinin, doğal dağılımını aştığı takdirde farklı bir X- diyagramı kullanılarak prosesin kusurlu yüzdesinin kontrol altında kalmasına çalışılmaktadır. Bu durumda kontrol diyagramının limitleri proses ortalamasının standart düzeyi yerine mamülün spesifikasyon limitlerine dayalı olmaktadır. Örnek ortalaması bu limitler içinde kaldığı sürece, proses kabul edilebilir varsayılacaktır. Proses ortalamasının sabit kaldığı varsayımı ortadan kalkacak ve bu değişmeler, istenmeyen düzeyde kusurlu parça yüzdesi imaline yol açan bir proses ortaya çıkmadıkça, proses ortalamasının spesifikasyon limitleri içinde değişmeler göstermesine izin verilecektir. Bu türden X diyagramları “kabul kontrol diyagramları” olarak isimlendirilmektedir.[]
Birikimli toplam kontrol diyagramları
Daha önce ele alınmış olan kontrol diyagramları, bu tür diyagramları ilk defa ortaya koyan ve uygulayan kimsenin adına izafeten “Shewhart” diyagramları olarak adlandırılmaktaydı. Bu diyagramların kullanılmasında temel kural, genellikle orta çizgiden 3σ uzaklıktaki kontrol limitleri dışına taşma olduğunda gerekli önlemlerin alınmasıdır. Orta çizgiden 2σ uzaklıktaki limitler ise uyarı limitleri olarak adlandırılır ve bu limitler dışına birbiri peşi sıra iki noktanın taşması harekete geçmek için tetikleyici olmaktadır. Walter A. Shewhart diyagramları ile ilgili uygulamalarda elde edilen gelişmelerin ışığında, verilerin tamamı veya son birkaç örneği göz önünde bulundurmaksızın harekete geçmek için yeni bir kuralın saptanması zorunluluğu ortaya çıkmıştır. Bu amaçla ilk defa 1954 yılında İngiliz istatistik uzmanı E. S. Page tarafından “Birikimli toplam kontrol diyagramları” ortaya konmuş ve diğer bazı İngiliz istatistikçiler tarafından geliştirilmiştir.
Birikimli toplam kontrol diyagramları, temel olarak bir prosesin sürekli kontrolünün sağlanması amacıyla kullanılmaktadır. Shewhart diyagramlarına karşı başlıca üstünlüğü, daha düşük maliyette aynı etkinliği sağlamasıdır. Özellikle değişimin fazla büyük olmadığı durumlarda, proses ortalamasındaki ani ve ısrarlı değişme birikimli toplam kontrol diyagramlarında derhal fark edilmekte, değişmenin zamanı daha belirgin olarak saptanabilmekte ve gösterilebilmektedir. Birikimli toplam kontrol diyagramlarında herhangi bir karara varılırken verilerden elde edilen bilgilerin tümünün kullanılması gerekmemektedir.
Kontrol diyagramı çeşitleri
| Diyagram Türü | Süreç gözlemi | Süreç gözlemlerinin ilişkileri | Süreç Gözlem Tipi | Saptanacak değişimin büyüklüğü | |
|---|---|---|---|---|---|
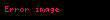 aritmetik ortalama ve R açıklık diyagramı | Bir alt gruptaki kalite özelliklerinin ölçümü | Bağımsız | Değişkenler | Büyük (≥ 1.5σ) | |
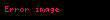| aritmetik ortalama ve s standart sapma diyagramı | Bir alt gruptaki kalite özelliklerinin ölçümü | Bağımsız | Değişkenler | Büyük (≥ 1.5σ) | |
| Shewhard bireysel kontrol diyagramı (ImR veya XmR diyagramları) | Bir gözlemdeki kalite özelliklerinin ölçülmesi | Bağımsız | Değişkenler | Büyük (≥ 1.5σ) | |
| Üç Yollu Kontrol Diyagramı | Bir alt gruptaki kalite özelliklerinin ölçülmesi | Bağımsız | Değişkenler | Büyük (≥ 1.5σ) | |
| p-diyagramı | Bir alt gruptaki uygun olmayan oranlar | Bağımsız | Nitelikler | Büyük (≥ 1.5σ) | |
| np-diyagramı | Bir alt gruptaki uygun olmayan sayılar | Bağımsız | Nitelikler | Büyük (≥ 1.5σ) | |
| c-diyagramı | Bir alt gruptaki uygun olmayan eleman sayısı | Bağımsız | Nitelikler | Büyük (≥ 1.5σ) | |
| u-diyagramı | Bir alt gruptaki birim başına düşen uygun olmayan eleman sayısı | Bağımsız | Nitelikler | Büyük (≥ 1.5σ) | |
| EWMA diyagramı (Üstel Ağırlıklandırmalı Hareketli Ortalamalar) | Üstel Ağırlıklandırmalı Hareketli Ortalamalar Moving average - Wikipedia, the free encyclopedia 30 Kasım 2011 tarihinde Wayback Machine sitesinde arşivlendi. Bir alt gruptaki kalite özelliklerinin üstel ağırlıklandırmalı hareketli ortalamaları | Bağımsız | Değişkenler veya Nitelikler | Küçük (< 1.5σ) | |
| CUSUM diyagramı | Bir alt gruptaki kalite özelliklerinin birikimli toplamı (Cumulative sum of quality characteristic measurement) | Bağımsız | Değişkenler veya Nitelikler | Küçükl (< 1.5σ) | |
| Zaman Serileri modeli | Bir alt gruptaki kalite özelliklerinin ölçümü | Kendiliğinden ilişkili | Değişkenler veya Nitelikler | Yok | |
| Regresyon Kontrol Diyagramı | Bir alt gruptaki kalite özelliklerinin ölçümü | Süreç kontrol değişkenlerine bağlı | Değişkenler | Büyük (≥ 1.5σ) | |
| Gerçek zamanlı karşılaştıran diyagramlar | Bir alt gruptaki kalite özelliklerinin ölçümü | Bağımsız | Değişkenler veya Nitelikler | Küçük (< 1.5σ) |
Nasıl çizilir?
Çizerken şu adımlar izlenir:
- Kullanılacak kalite karakteristiği belirlenir. Bunun için en çok hata meydana getire özelliğe öncelik verilir ve nihai mamülün kalitesini etkileyen proses değişkenleri ve koşulları tanımlanır.
- En uygun kontrol diyagramı türü çizilir.
- Kullanılacak orta çizgi ve kontrol limitlerinin hesaplanmasındaki kriterler saptanır.
- Kontrol diyagramında kullanılacak veri kümeleri seçilir ve kronolojik olarak kontrol diyagramına yerleştirilir.
- Veri toplamasında kullanılacak sistem oluşturulur. Kontrol diyagramı sadece günlük amaçlar için kullanılacaksa basit ve kullanışlı olmalıdır.
- Sonuçların yorumlanmasında uygulanacak kurallar belirlenir ve kontrol limitleri hesaplanır.
Uygulama alanları
- Aritmetik ortalama, dağılma aralığı ve standart sapma türünden istatistiksel ölçümlerle ilgili değişkenler için kontrol diyagramlarının genel uygulama alanı, tekil özelliklerin kontrolünü kapsamaktadır.
- Kusurlu parça yüzdesi (p) ve kusurlu parça sayısı (c) türünden istatistiksel ölçümlerle ilgili özellikler için kontrol diyagramlarının genel uygulama alanı, prosesteki toplam kusurlu parçanın kontrolünü kapsamaktadır.
Kaynakça
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kontrol diyagrami bir kalite izleme diyagramidir Dogada toplumda ve insan etkisi ile meydana gelen tum olaylarda degiskenlik bilinen bir olgudur Bu nedenle uretim surecinde cesitli nedenlerin etkisi sonucu degiskenligin ortaya cikmasi dogal ve kacinilmaz kabul edilmektedir Aslinda kalite kontrol faaliyetlerinin temel amaci uretim surecinin ekonomik olmasi kosulu ile kontrol altinda tutulmasidir Buradaki ekonomiklik ile ifade edilmek istenen husus kontrolun gerceklestirilmesi icin harcanan cabalarla elde edilen yararlar arasinda bir dengenin saglanmasidir Bu asamada kontrol icin kullanilan diyagramlarin tanimina gelirsek proses kontrolunun istatistik yontemlerle ekonomik ve guvenilir bicimde gerceklestirilebilmesinde kullanilan baslica arac kontrol diygramlaridir Armand V Feigenbaum kontrol diyagramini mamulun mamulu olusturan parcalarin veya diger bilesenlerin kalite spesifikasyonlarini gecmis deneyimlere dayanarak saptanan limitlere gore kronolojik olarak karsilastirmaya yarayan grafik arac olarak tanimlamaktadir TurleriKabul kontrol diyagramlari Belirli bir boyut icin muhendislik toleransi imalat prosesinin dogal dagilimini astigi takdirde farkli bir X diyagrami kullanilarak prosesin kusurlu yuzdesinin kontrol altinda kalmasina calisilmaktadir Bu durumda kontrol diyagraminin limitleri proses ortalamasinin standart duzeyi yerine mamulun spesifikasyon limitlerine dayali olmaktadir Ornek ortalamasi bu limitler icinde kaldigi surece proses kabul edilebilir varsayilacaktir Proses ortalamasinin sabit kaldigi varsayimi ortadan kalkacak ve bu degismeler istenmeyen duzeyde kusurlu parca yuzdesi imaline yol acan bir proses ortaya cikmadikca proses ortalamasinin spesifikasyon limitleri icinde degismeler gostermesine izin verilecektir Bu turden X diyagramlari kabul kontrol diyagramlari olarak isimlendirilmektedir kaynak belirtilmeli Birikimli toplam kontrol diyagramlari Daha once ele alinmis olan kontrol diyagramlari bu tur diyagramlari ilk defa ortaya koyan ve uygulayan kimsenin adina izafeten Shewhart diyagramlari olarak adlandirilmaktaydi Bu diyagramlarin kullanilmasinda temel kural genellikle orta cizgiden 3s uzakliktaki kontrol limitleri disina tasma oldugunda gerekli onlemlerin alinmasidir Orta cizgiden 2s uzakliktaki limitler ise uyari limitleri olarak adlandirilir ve bu limitler disina birbiri pesi sira iki noktanin tasmasi harekete gecmek icin tetikleyici olmaktadir Walter A Shewhart diyagramlari ile ilgili uygulamalarda elde edilen gelismelerin isiginda verilerin tamami veya son birkac ornegi goz onunde bulundurmaksizin harekete gecmek icin yeni bir kuralin saptanmasi zorunlulugu ortaya cikmistir Bu amacla ilk defa 1954 yilinda Ingiliz istatistik uzmani E S Page tarafindan Birikimli toplam kontrol diyagramlari ortaya konmus ve diger bazi Ingiliz istatistikciler tarafindan gelistirilmistir Birikimli toplam kontrol diyagramlari temel olarak bir prosesin surekli kontrolunun saglanmasi amaciyla kullanilmaktadir Shewhart diyagramlarina karsi baslica ustunlugu daha dusuk maliyette ayni etkinligi saglamasidir Ozellikle degisimin fazla buyuk olmadigi durumlarda proses ortalamasindaki ani ve israrli degisme birikimli toplam kontrol diyagramlarinda derhal fark edilmekte degismenin zamani daha belirgin olarak saptanabilmekte ve gosterilebilmektedir Birikimli toplam kontrol diyagramlarinda herhangi bir karara varilirken verilerden elde edilen bilgilerin tumunun kullanilmasi gerekmemektedir Kontrol diyagrami cesitleriDiyagram Turu Surec gozlemi Surec gozlemlerinin iliskileri Surec Gozlem Tipi Saptanacak degisimin buyuklugux displaystyle bar x aritmetik ortalama ve R aciklik diyagrami Bir alt gruptaki kalite ozelliklerinin olcumu Bagimsiz Degiskenler Buyuk 1 5s x displaystyle bar x aritmetik ortalama ve s standart sapma diyagrami Bir alt gruptaki kalite ozelliklerinin olcumu Bagimsiz Degiskenler Buyuk 1 5s Shewhard bireysel kontrol diyagrami ImR veya XmR diyagramlari Bir gozlemdeki kalite ozelliklerinin olculmesi Bagimsiz Degiskenler Buyuk 1 5s Uc Yollu Kontrol Diyagrami Bir alt gruptaki kalite ozelliklerinin olculmesi Bagimsiz Degiskenler Buyuk 1 5s p diyagrami Bir alt gruptaki uygun olmayan oranlar Bagimsiz Nitelikler Buyuk 1 5s np diyagrami Bir alt gruptaki uygun olmayan sayilar Bagimsiz Nitelikler Buyuk 1 5s c diyagrami Bir alt gruptaki uygun olmayan eleman sayisi Bagimsiz Nitelikler Buyuk 1 5s u diyagrami Bir alt gruptaki birim basina dusen uygun olmayan eleman sayisi Bagimsiz Nitelikler Buyuk 1 5s EWMA diyagrami Ustel Agirliklandirmali Hareketli Ortalamalar Ustel Agirliklandirmali Hareketli Ortalamalar Moving average Wikipedia the free encyclopedia 30 Kasim 2011 tarihinde Wayback Machine sitesinde arsivlendi Bir alt gruptaki kalite ozelliklerinin ustel agirliklandirmali hareketli ortalamalari Bagimsiz Degiskenler veya Nitelikler Kucuk lt 1 5s CUSUM diyagrami Bir alt gruptaki kalite ozelliklerinin birikimli toplami Cumulative sum of quality characteristic measurement Bagimsiz Degiskenler veya Nitelikler Kucukl lt 1 5s Zaman Serileri modeli Bir alt gruptaki kalite ozelliklerinin olcumu Kendiliginden iliskili Degiskenler veya Nitelikler YokRegresyon Kontrol Diyagrami Bir alt gruptaki kalite ozelliklerinin olcumu Surec kontrol degiskenlerine bagli Degiskenler Buyuk 1 5s Gercek zamanli karsilastiran diyagramlar Bir alt gruptaki kalite ozelliklerinin olcumu Bagimsiz Degiskenler veya Nitelikler Kucuk lt 1 5s Nasil cizilir Cizerken su adimlar izlenir Kullanilacak kalite karakteristigi belirlenir Bunun icin en cok hata meydana getire ozellige oncelik verilir ve nihai mamulun kalitesini etkileyen proses degiskenleri ve kosullari tanimlanir En uygun kontrol diyagrami turu cizilir Kullanilacak orta cizgi ve kontrol limitlerinin hesaplanmasindaki kriterler saptanir Kontrol diyagraminda kullanilacak veri kumeleri secilir ve kronolojik olarak kontrol diyagramina yerlestirilir Veri toplamasinda kullanilacak sistem olusturulur Kontrol diyagrami sadece gunluk amaclar icin kullanilacaksa basit ve kullanisli olmalidir Sonuclarin yorumlanmasinda uygulanacak kurallar belirlenir ve kontrol limitleri hesaplanir Uygulama alanlariAritmetik ortalama dagilma araligi ve standart sapma turunden istatistiksel olcumlerle ilgili degiskenler icin kontrol diyagramlarinin genel uygulama alani tekil ozelliklerin kontrolunu kapsamaktadir Kusurlu parca yuzdesi p ve kusurlu parca sayisi c turunden istatistiksel olcumlerle ilgili ozellikler icin kontrol diyagramlarinin genel uygulama alani prosesteki toplam kusurlu parcanin kontrolunu kapsamaktadir Kaynakca a b A V Feigenbaum Total Quality Control a g e p 396 Tapiero Charles S 1996 The Management of Quality and its Control Great Britain Chapman amp Hall ISBN 0 412 55720 7 Besterfield Dale H 2004 Quality Control 7th Edition Pearson Prentice Hall ISBN 0 13 191135 X Ayrica bakinizYedi kalite araci