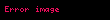Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan x2 − 4x + 7, ikinci dereceden oluşan bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olma zorunluluğu vardır 2. terimde x′i ele alan bir bölme işlemi x'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2).

=1/4(x+4)(x+1)(x-2)
Polinomlar, bilimde ve matematik alanında sıkça görülür. Ekonomiden kimyaya, kimyadan fiziğe ve sosyal bilimlerde problemlerin çözülmesi için kullanılır. Polinomlar, toplama işlemlerinde ve sayısal analizlerde diğer fonksiyonları belirlemek için kullanılır. İleri seviye matematikte, polinomlar, polinom halkaları oluşturmak için kullanılır ve bu halkalar temel matematikte ve cebirsel geometride kullanılan merkezi bir kavramdır.
Bu ismin akılda kalması amacıyla, Türk Dil Kurumu'nun da belirttiği polinom sözlük anlamıyla "çok terimli" anlamına gelmektedir.
Etimoloji
Oxford İngilizce Sözlüğü'ne göre, polinom, kelimesindeki bi- kökünün Yunanca "poli" kökü ile değiştirilmesiyle oluşmuş bir kelimedir. Yunanca kelime poli, çok anlamına gelmektedir. polinom kelimesi ilk 17. yüzyılda kullanılmıştır.
Notasyon
Bir polinomda belirsiz X, formüllerde P ya da P(X) olarak belirebilir.
Genelde, polinomun ismi P(X) değil, P′dir. Ancak, eğer a bir sayı, bir değişken, başka bir polinom, veya, daha genel olarak herhangi bir ifadeyi belirtmek için kullanılırsa, P(a) teamül olarak P′deki X′in yerine a′nın geçmesini belirtir. Örnek olarak polinom P, yandaki fonksiyonu tanımlar: 
İlişkilendirilen fonksiyonda bilinmeyenler için büyük harf ve değişkenler için küçük harf kullanmak bilinen bir uzlaşımdır.
Özellikle, eğer a = X olursa, P(a)′nın tanımı P = P(X)′i belirtir.
Bu eşitlik bazı durumlarda sözle ifade etmeyi basitleştirir. Örneğin ″P(X) bir polinom olsun″ yerine ″X bilinmeyeni içinde P bir polinom olsun″ kullanılır. Diğer yandan, bilinmeyenin ismini vurgulamak gerekli olmadığı zaman, eğer polinomun her görünüşünde bilinmeyenin ismi gözükmüyorsa çoğu formül daha basit ve okuması daha kolay olur.
Polinomların Aritmetiği
Toplama
Polinomlar toplamanın birleşmeli yasasını kullanarak (bütün terimlerin tek bir toplamda birleştirilmesi), mümkün olduğunca tekrar sıralanıp, benzeri terimler birleştirilebilir.
Örneğin:
olsun
olsun
- sonrasında
- basitleştirirsek:
Polinomların toplamı polinom verir.
Katsayılar Toplamı: Bir polinomun katsayılar toplamını bulabilmek için o polinomun tüm değişkenlerine 1 vermeliyiz.
Örneğin:
P(3x+2)'in katsayılar toplamı P(5).

Polinomun sadece çift dereceli terimlerinin katsayılar toplamını bulabilmek için değişkenlere 1 ve -1 değerlerini vererek çıkan sonucu toplar ve ikiye böleriz. Sadece tek dereceli terimlerim katsayılar toplamı için ise aradaki toplama işlemini çıkarma işlemine çevirerek sonuca ulaşmak mümkündür.
Çarpım
İki polinomun çarpımlarının terimlerinin toplamını çözmek için, dağılma yasası tekrar edecek şekilde uygulanılır, ki bu, bir polinomun her teriminin diğer polinomun her terimiyle çarpılmasıyla sonuçlanır.
Örneğin:
olsun
olsun
- sonrasında
- basitleştirirsek:
Polinomların çarpımı polinom verir.
Bölme
Polinom değerlendirmesi birinci dereceden bir polinomun kalanı hesaplamak için kullanılabilir, çünkü f(x)′in (x − a)′ya bölümü f(a)′dir; bakınız. Bu yöntem oran gerekli olmadığı zaman, çoğunlukta kullanılan bölüm algoritmasından daha verimli olur.
Diğer Özellikler
- İki polinomun bileşke fonksiyonu bir polinomdur, ki bu ilk polinomdaki değişkenin ikinci polinomdaki bir değişkenle değiştirilmesiyle elde edilir.
- anxn + an−1xn−1 + ... + a2x2 + a1x + a0 polinomunun türevi: nanxn−1 + (n−1)an−1xn−2 + ... + 2a2x + a1′dir. Eğer katsayı dizisi tam sayı içermezse (örneğin katsayılar asal sayı olan p′nin modülosu ise), o zaman kak, k kere ak′nin toplamı olarak yorumlanmalıdır. Örneğin tam sayı üstünde modülo p iken, xp + 1′nin türevi polinom 0′dır.
- Özel olarak; bir polinomun derecesi 3 ise polinoma kübik, derecesi 2 ise kuadratik, derecesi 1 ise doğrusal veya lineer, derecesi 0 ise (P(x)≠0) sabit polinom denir.
- Sıfıra eşit olan bir polinoma sıfır polinomu denir ama sıfır polinomun derecesi 0 değildir. Sıfır polinomunun derecesi tanımlanmamıştır.
Hermit polinomları
Hermit polinomları Pierre-Simon Laplace tarafından 1810'da zor anlaşılır bir biçimde tanımlanmış ve 1859'da Pafnuty Chebyshev tarafından ayrıntılı olarak incelenmiştir. Diğer klasik dik polinomlar gibi, Hermit polinomları birkaç farklı başlangıç noktasından tanımlanabilir.

Tanım
Olasılıkçıların kullandığı Hermit polinomu;

Fizikçilerin kullandığı Hermit polinomu;
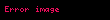
Olasılıkçıların kullandığı Hermit polinomunun ilk on bir değeri;





 ) Hermit polinomunun ilk altı değer grafiği
) Hermit polinomunun ilk altı değer grafiği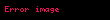



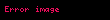

Özellikleri




Diklik



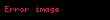
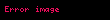
ya da


Ayrıca bakınız
Kaynakça
- ^ . 8 Aralık 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Aralık 2013.
- ^ "polynomial" kelimesinin köken bilgisi. Sıkıştırılmış Oxford İngilizce Sözlüğü
- ^ a b Edwards, Harold M. (1995). Linear Algebra (İngilizce). Springer. s. 47. ISBN . 2 Ocak 2014 tarihinde kaynağından . Erişim tarihi: 11 Aralık 2013.
- ^ Salomon, David (2006). Coding for Data and Computer Communications (İngilizce). Springer. s. 459. ISBN . 2 Ocak 2014 tarihinde kaynağından . Erişim tarihi: 11 Aralık 2013.
- ^ a b c Barbeau, E.J. (2003). Polynomials (İngilizce). Springer. ss. 1-2. ISBN . 28 Mart 2016 tarihinde kaynağından . Erişim tarihi: 13 Eylül 2020.
- ^ Barbeau, E.J. (2003). Polynomials (İngilizce). Springer. ss. 64-65. ISBN . 2 Ocak 2014 tarihinde kaynağından . Erişim tarihi: 11 Aralık 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir polinom belirli sayida bagimsiz degisken ve sabit sayidan olusan bir ifadedir Polinom kendi icinde toplama cikarma carpma ve negatif olmayan sayinin ussunu alma islemlerini kullanir Ornek olarak tek bilinmeyenli bir polinom olan x2 4x 7 ikinci dereceden olusan bir polinomdur Diger bir ornek olarak x2 4 x 7x3 2 bir polinom degildir cunku polinomlarda terimlerin derecelerinin dogal sayi olma zorunlulugu vardir 2 terimde x i ele alan bir bolme islemi x in derecesini negatif yapmaktadir ve 3 terim dogal sayi olmayan bir derece icermektedir 3 2 3 dereceden bir polinomun grafigi 1 4 x3 3x2 6x 8 displaystyle 1 4 x 3 3x 2 6x 8 1 4 x 4 x 1 x 2 Polinomlar bilimde ve matematik alaninda sikca gorulur Ekonomiden kimyaya kimyadan fizige ve sosyal bilimlerde problemlerin cozulmesi icin kullanilir Polinomlar toplama islemlerinde ve sayisal analizlerde diger fonksiyonlari belirlemek icin kullanilir Ileri seviye matematikte polinomlar polinom halkalari olusturmak icin kullanilir ve bu halkalar temel matematikte ve cebirsel geometride kullanilan merkezi bir kavramdir Bu ismin akilda kalmasi amaciyla Turk Dil Kurumu nun da belirttigi polinom sozluk anlamiyla cok terimli anlamina gelmektedir EtimolojiOxford Ingilizce Sozlugu ne gore polinom kelimesindeki bi kokunun Yunanca poli koku ile degistirilmesiyle olusmus bir kelimedir Yunanca kelime poli cok anlamina gelmektedir polinom kelimesi ilk 17 yuzyilda kullanilmistir NotasyonBir polinomda belirsiz X formullerde P ya da P X olarak belirebilir Genelde polinomun ismi P X degil P dir Ancak eger a bir sayi bir degisken baska bir polinom veya daha genel olarak herhangi bir ifadeyi belirtmek icin kullanilirsa P a teamul olarak P deki X in yerine a nin gecmesini belirtir Ornek olarak polinom P yandaki fonksiyonu tanimlar x P x displaystyle x mapsto P x Iliskilendirilen fonksiyonda bilinmeyenler icin buyuk harf ve degiskenler icin kucuk harf kullanmak bilinen bir uzlasimdir Ozellikle eger a X olursa P a nin tanimi P P X i belirtir Bu esitlik bazi durumlarda sozle ifade etmeyi basitlestirir Ornegin P X bir polinom olsun yerine X bilinmeyeni icinde P bir polinom olsun kullanilir Diger yandan bilinmeyenin ismini vurgulamak gerekli olmadigi zaman eger polinomun her gorunusunde bilinmeyenin ismi gozukmuyorsa cogu formul daha basit ve okumasi daha kolay olur Polinomlarin AritmetigiToplama Polinomlar toplamanin birlesmeli yasasini kullanarak butun terimlerin tek bir toplamda birlestirilmesi mumkun oldugunca tekrar siralanip benzeri terimler birlestirilebilir Ornegin P 3x2 2x 5xy 2 displaystyle P 3x 2 2x 5xy 2 olsun Q 3x2 3x 4y2 8 displaystyle Q 3x 2 3x 4y 2 8 olsun sonrasinda P Q 3x2 2x 5xy 2 3x2 3x 4y2 8 displaystyle P Q 3x 2 2x 5xy 2 3x 2 3x 4y 2 8 basitlestirirsek P Q x 5xy 4y2 6 displaystyle P Q x 5xy 4y 2 6 Polinomlarin toplami polinom verir Katsayilar Toplami Bir polinomun katsayilar toplamini bulabilmek icin o polinomun tum degiskenlerine 1 vermeliyiz Ornegin P 3x 2 in katsayilar toplami P 5 Cift dereceli terimlerin katsayilarinin toplami Polinomun sadece cift dereceli terimlerinin katsayilar toplamini bulabilmek icin degiskenlere 1 ve 1 degerlerini vererek cikan sonucu toplar ve ikiye boleriz Sadece tek dereceli terimlerim katsayilar toplami icin ise aradaki toplama islemini cikarma islemine cevirerek sonuca ulasmak mumkundur Carpim Iki polinomun carpimlarinin terimlerinin toplamini cozmek icin dagilma yasasi tekrar edecek sekilde uygulanilir ki bu bir polinomun her teriminin diger polinomun her terimiyle carpilmasiyla sonuclanir Ornegin P 2x 3y 5 displaystyle color BrickRed P 2x 3y 5 olsun Q 2x 5y xy 1 displaystyle color RoyalBlue Q 2x 5y xy 1 olsun sonrasinda PQ 2x 2x 2x 5y 2x xy 2x 1 3y 2x 3y 5y 3y xy 3y 1 5 2x 5 5y 5 xy 5 1 displaystyle begin array rccrcrcrcr color BrickRed P color RoyalBlue Q amp amp amp color BrickRed 2x cdot color RoyalBlue 2x amp amp color BrickRed 2x cdot color RoyalBlue 5y amp amp color BrickRed 2x cdot color RoyalBlue xy amp amp color BrickRed 2x cdot color RoyalBlue 1 amp amp amp color BrickRed 3y cdot color RoyalBlue 2x amp amp color BrickRed 3y cdot color RoyalBlue 5y amp amp color BrickRed 3y cdot color RoyalBlue xy amp amp color BrickRed 3y cdot color RoyalBlue 1 amp amp amp color BrickRed 5 cdot color RoyalBlue 2x amp amp color BrickRed 5 cdot color RoyalBlue 5y amp amp color BrickRed 5 cdot color RoyalBlue xy amp amp color BrickRed 5 cdot color RoyalBlue 1 end array basitlestirirsek PQ 4x2 21xy 2x2y 12x 15y2 3xy2 28y 5 displaystyle PQ 4x 2 21xy 2x 2 y 12x 15y 2 3xy 2 28y 5 Polinomlarin carpimi polinom verir Bolme Polinom degerlendirmesi birinci dereceden bir polinomun kalani hesaplamak icin kullanilabilir cunku f x in x a ya bolumu f a dir bakiniz Bu yontem oran gerekli olmadigi zaman cogunlukta kullanilan bolum algoritmasindan daha verimli olur Diger Ozellikler Iki polinomun bileske fonksiyonu bir polinomdur ki bu ilk polinomdaki degiskenin ikinci polinomdaki bir degiskenle degistirilmesiyle elde edilir anxn an 1xn 1 a2x2 a1x a0 polinomunun turevi nanxn 1 n 1 an 1xn 2 2a2x a1 dir Eger katsayi dizisi tam sayi icermezse ornegin katsayilar asal sayi olan p nin modulosu ise o zaman kak k kere ak nin toplami olarak yorumlanmalidir Ornegin tam sayi ustunde modulo p iken xp 1 nin turevi polinom 0 dir Ozel olarak bir polinomun derecesi 3 ise polinoma kubik derecesi 2 ise kuadratik derecesi 1 ise dogrusal veya lineer derecesi 0 ise P x 0 sabit polinom denir Sifira esit olan bir polinoma sifir polinomu denir ama sifir polinomun derecesi 0 degildir Sifir polinomunun derecesi tanimlanmamistir Hermit polinomlariHermit polinomlari Pierre Simon Laplace tarafindan 1810 da zor anlasilir bir bicimde tanimlanmis ve 1859 da Pafnuty Chebyshev tarafindan ayrintili olarak incelenmistir Diger klasik dik polinomlar gibi Hermit polinomlari birkac farkli baslangic noktasindan tanimlanabilir Ilk alti Hermit polinomunun deger grafigiTanim Olasilikcilarin kullandigi Hermit polinomu Hen x 1 ne x22 dndxne x22 textstyle He n x 1 n e left frac x 2 2 right d n over dx n e left frac x 2 2 right Fizikcilerin kullandigi Hermit polinomu Hn x 1 nex2dndxne x2 displaystyle H n x 1 n e x 2 d n over dx n e x 2 Olasilikcilarin kullandigi Hermit polinomunun ilk on bir degeri He0 x 1 displaystyle He 0 x 1 He1 x x displaystyle He 1 x x He2 x x2 1 textstyle He 2 x x 2 1 He3 x x3 3x textstyle He 3 x x 3 3x Fizikcilerin kullandigi Hn displaystyle H n Hermit polinomunun ilk alti deger grafigi He4 x x4 6x2 3 textstyle He 4 x x 4 6x 2 3 He5 x x5 10x3 15x textstyle He 5 x x 5 10x 3 15x He6 x x6 15x4 45x2 15 textstyle He 6 x x 6 15x 4 45x 2 15 He7 x x7 21x5 105x3 105x textstyle He 7 x x 7 21x 5 105x 3 105x He8 x x8 28x6 210x4 420x2 105 textstyle He 8 x x 8 28x 6 210x 4 420x 2 105 He9 x x9 36x7 378x5 1260x3 945x textstyle He 9 x x 9 36x 7 378x 5 1260x 3 945x He10 x x10 45x8 630x6 3150x4 4725x3 945 textstyle He 10 x x 10 45x 8 630x 6 3150x 4 4725x 3 945 Ozellikleri n displaystyle n dereceden bir Hermit polinomu n displaystyle n dereceleri bir polinomdur Olasilikcilarin Hen displaystyle He n kullandigi Hermit polinomunun ilk terimindeki katsayisi 1 dir Fiziklerin kullandigi Hermit polinomunun katsayisi 2n displaystyle 2 n Diklik Hen displaystyle He n ve Hn displaystyle H n n displaystyle n dereceden polinomlari icin n 1 2 3 4 displaystyle n 1 2 3 4 Bu polinomlar agirlik islevine fonksiyon gore dikliktir w x e x22 He displaystyle w x e left frac x 2 2 right He icin ya da w x e x2 displaystyle w x e x 2 H displaystyle H icin Ayrica bakinizMatematiksel fonksiyonlar listesiKaynakca 8 Aralik 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 17 Aralik 2013 polynomial kelimesinin koken bilgisi Sikistirilmis Oxford Ingilizce Sozlugu a b Edwards Harold M 1995 Linear Algebra Ingilizce Springer s 47 ISBN 9780817637316 2 Ocak 2014 tarihinde kaynagindan Erisim tarihi 11 Aralik 2013 Salomon David 2006 Coding for Data and Computer Communications Ingilizce Springer s 459 ISBN 9780387238043 2 Ocak 2014 tarihinde kaynagindan Erisim tarihi 11 Aralik 2013 a b c Barbeau E J 2003 Polynomials Ingilizce Springer ss 1 2 ISBN 9780387406275 28 Mart 2016 tarihinde kaynagindan Erisim tarihi 13 Eylul 2020 Barbeau E J 2003 Polynomials Ingilizce Springer ss 64 65 ISBN 9780387406275 2 Ocak 2014 tarihinde kaynagindan Erisim tarihi 11 Aralik 2013
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans