Akışkanlar statiği

Akışkan statiği ya da hidrostatik, hareketsiz akışkanlar üzerinde çalışmalar yapan akışkan mekaniğinin dalı. Hangi akışkanların durağan dengede hareketsiz kaldığıyla ilgili yapılan çalışmaları kabul eder ve akışkan dinamiğiyle karşılaştırıldığında hareket halindeki akışkanları inceler.

Hidrolik ve hidrostatik tablosu, 1728, Cyclopaedia

Hidrostatik depolama, taşıma ve akışkan kullanma için ekipman mühendisliği olan hidrolik için esastır. Ayrıca jeofizik, astrofizik, meteoroloji gibi birçok alanla ilgilidir.

Hidrostatik günlük hayatta yaşadığımız örneğin atmosfer basıncının neden rakımla değiştiği, neden tahta ya da zeytinyağının su yüzeyinde yüzdüğü veya su hangi şekle sahip kaba konulursa konulsun yüzeyinin neden yatay çizgi olarak gözüktüğü gibi birçok olaya fiziksel açıklama getirir.

Tarihçe

Hidrostatikle ilgili bazı prensipler deneye ve antik çağlardan beri sezgiye dayalı olarak bilinir. Arşimet aynı zamanda kendi adını taşıyan yer değiştiren sıvının hacim ve öz kütlesi için kaldırma kuvveti ile ilgili matematiksel yasayı keşfederek itibar sahibi olmuştur. Romalı mühendis Vitruvius okuyucularını boruların hidrostatik basınç altında patladığı hakkında uyarmıştır.

Basınç konsepti ve akışkanlar tarafından taşınma yolları Fransız matematikçi ve felsefeci Blaise Pascal tarafından 1647 yılında formüle edilmiştir.

Hareketsiz sıvılarda basınç

Akışkanların esas doğalarından dolayı, akışkanlar kayma gerilimi mevcudiyeti altında hareketsizliğini sürdüremezler. Fakat, akışkanlar etkileştiği her yüzeye normal basınç uygulayabilirler. Eğer akışkan içerisindeki bir nokta son derece küçük bir küp olarak düşünülürse, her kenardaki akışkan biriminin eşit olmak zorunda olduğunu söyleyen denge yasalarından sonuç çıkarılır. Eğer durum böyle değil ise, akışkan sonuçta oluşan kuvvete doğru hareket edecektir. Dahası, akışkan üzerindeki basınç izotropiktir. Her yöne doğru eşit büyüklükteymiş gibi davranır. Bu özellik akışkanlara boru ya da tüplere doğru iletme kuvveti verir. Kuvvet, taşınan akışkan tarafından borunun diğer ucuna kadar uygulanır. Bu prensip ilk olarak Blaise Pascal tarafından biraz gelişmiş formuyla formüle edildi ve günümüzde Pascal yasası olarak bilinmektedir.

Hidrostatik basınç

Hareketsiz akışkanlarda, bütün sürtünme gerilmesi ortadan kaybolmuştur ve sistemin gerilmesi hidrostatik olarak adlandırılmıştır. Bu şart Navier-Stokes denklemlerine uygulandığında, basıncın değişimi sadece gövde kuvveti haline gelir. için denge durumunda akışkan tarafından uygulanan korunan kuvvet alanı basıncı, yer çekimi kuvvet alanı gibi, yer çekimi tarafından uygulanan kuvvet olarak görev yapar haline gelir.

Hidrostatik basınç akışkanın son derece küçük derecede küpünün kontrol hacim analizi tarafından belirlenebilir. Basınç test yüzeyine etki eden kuvvet olarak tanımlandığından beri ve akışkanın herhangi bir son derece küçük küpüne etki eden tek kuvvet akışkan kolonunun üzerindeki ağırlıktır. Hidrostatik basınç formülle hesaplanabilir.

${\displaystyle p(z)-p(z_{0})={\frac {1}{A}}\int _{z_{0}}^{z}dz'\iint \limits _{A}dx'dy'\,\rho (z')g(z')=\int _{z_{0}}^{z}dz'\,\rho (z')g(z')}$

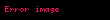
• p: hidrostatik basınç (Pa)
• ρ: akışkan yoğunluğu (kg/m³)
• g: yer çekimsel ivme (m/s²)
• A: test yüzeyi (m²)
• z: yer çekim yönüne paralel olan test yüzeyi yüksekliği (m)

Su ve diğer akışkanlar için, integral birçok pratik uygulama için iki varsayımı esas alarak önemli derecede basitleştirilmiştir. Birçok akışkan sıkıştırılamayan olarak düşünüldüğünden dolayı, makul olan tahminler öz kütleyi akışkan genelinde sabit varsayarak yapılmıştır. Aynı tahmin gaz ortamında yapılamaz. Ayrıca, akışkan kolonunun yer çekim yönüne paralel olan test yüzeyi yüksekliği ve basıncın sıfır referans noktasına göre yüksekliği arasındaki yükseklik genel olarak yer çekimi varyasyonu ihmal edilip Dünya yarıçapıyla karşılaştırıldığında küçüktür. Bu şartlar altında, integral basit bir formüle dönüşür:

${\displaystyle \ p-p_{0}=\rho gh}$

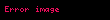
Basınç referans noktasının sıvı maddenin yüzeyinin altında veya yüzeyinde olması gerektiği not edilmelidir. Başka bir deyişle, integral iki ya da daha çok terime ayrılmalıdır. Örnek olarak, mutlak basınç vakumla karşılaştırıldığında:

${\displaystyle p=\rho gH+p_{\mathrm {atm} }}$

Basınç hava kolonun üzerinde geriye kalan integralden sonsuza giden sıvı madde yüzeyine kadar hesaplanabilir. Bu basınç prizması kullanılarak görselleştirilebilir.

Hidrostatik basınç gıdaların korunması sürecinde kullanılır.

Atmosfer basıncı

İstatistiksel mekanikler sabit derecedeki gaz için gösterir ki:

${\displaystyle \ p(h)=p(0)e^{-Mgh/kT}}$

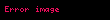
• g: yer çekiminden dolayı oluşan ivme
• T: Mutlak sıcaklık
• k: Boltzmann sabiti
• M: Tek gaz molekülünün kütlesi
• p: basınç
• h: yükseklik

Barometrik formül olarak bilinir ve basıncı hidrostatik varsayımından türetilebilir.

Eğer gazın içerisinde birçok molekül tipi varsa, her tipin kısmi basıncı bu denklem tarafından verilir. Birçok şart altında, her gaz türünün dağılımı diğer türlerden bağımsızdır.

Kaldırma kuvveti

Bir akışkan içerisine tamamen ya da kısmen batmış herhangi bir şekle sahip cisim yerel basıncın tersi yönünde bir net kuvvetle karşılaşacaktır. Eğer bu basınç yer çekiminden dolayı oluşursa, dik doğrultudaki net kuvvet yer çekim kuvvetine zıt yönlü olacaktır. Bu zıt kuvvet kaldırma kuvveti olarak adlandırılır ve eşit büyüklükte fakat yer değiştiren sıvının ağırlığı kadar olmak için zıt yöndedir. Matematiksel olarak:

${\displaystyle F=\rho gV}$

Örnek olarak, geminin yüzmesi durumunda, cismin kütlesi yüzmesine olanak tanıyan suyun çevresindeki kuvvetlerin basıncı tarafından dengelenmiştir.

Eğer gemiye ağırlık yüklenmeye devam ederse, su içerisine daha çok batar, daha çok su yer değiştirir ve dahası artan kütleyi dengelemek için daha çok kaldırma kuvveti elde edilir.

Kaldırma kuvveti prensibinin keşfi Arşimet yasasına dayandırılmaktadır.

Batmış yüzeyler için hidrostatik kuvvet

Hidrostatik kuvvetin yatay ve dikey bileşenleri batmış yüzeyler için formülle ifade edilir:

${\displaystyle F_{H}=p_{c}A}$

${\displaystyle F_{V}=\rho gV}$

• p_c: batmış cismin dik izdüşümünün merkezindeki basınç
• A: yüzeyin aynı dik iz düşüme sahip alanı
• ρ: akışkanın öz kütlesi
• g: yer çekiminden dolayı oluşan ivme
• V: eğimli yüzeyinin hemen üzerindeki akışkanın hacmi

Serbest sıvı maddeler

Sıvılar gazlarla ya da vakumla birlikte arayüz oluşturabilen serbest yüzeye sahip olabilirler. Genellikle, kayma gerilmesini devam ettirme yeteneği eksikliği serbest yüzeyin düzensiz olarak dengeye karşı ayarlanmasına neden olur. Fakat, kısa uzunluk ölçümlerinde yüzey geriliminden oluşan önemli dengeleyici kuvvet vardır.

Kılcal hareket

İlgili uzunluk ölçüleriyle karşılaştırıldığında boyutları küçük kanal içerisindeki sıvı zorla hareket ettirilirse, yüzey gerilimi etkisi önemli kılcal hareket yoluyla menüsküs oluşumuna neden olur. Bu kılcal hareket odun borusu içerisindeki akan suyu hareket ettirme mekanizmasına sahip olduğundan biyolojik sistemler için önemli sonuçlara sahiptir.

Asılı damlalar

Yüzey gerilimsiz, damlalar şekle sahip olamaz. Damlanın boyutları ve durağanlığı yüzey gerilimi tarafından karar verilir. Damlanın yüzey gerilimi doğrudan akışkanın kohezyon özelliğiyle orantılıdır.

Kaynakça

1. ^ Marcus Vitruvius Pollio (ca. 15 BCE), "The Ten Books of Architecture", Book VIII, Chapter 6. At the University of Chicago's Penelope site. Accessed on 2013-02-25.
2. ^ Brown, Amy Christian (2007). Understanding Food: Principles and Preparation (3 bas.). Cengage Learning. s. 546. ISBN . 1 Ekim 2014 tarihinde kaynağından . Erişim tarihi: 20 Ocak 2015. 
3. ^ ^{a b} Fox, Robert; McDonald, Alan; Pritchard, Philip (2012). Fluid Mechanics (8 bas.). . ss. 76-83. ISBN . 

Dış bağlantılar

• J.B. Calvert (2003) Denver Üniversitesi, Hidrostatik9 Şubat 2014 tarihinde Wayback Machine sitesinde .