Bu madde, uygun değildir. (Mayıs 2015) |
Hipotez testi, bir hipotezin doğruluğunun istatistiksel bir güvenilirlik aralığında saptanması için kullanılan yöntem.
Hipotez testleri bir örneklem ortalaması ile bu örneklemin çekilmiş olduğu düşünülen ortalama değer etrafındaki farkın anlamlı olup olmadığını (yani önemli bir fark olup olmadığını) saptayan testlerdir.
Eğer iki ana kütlenin ortalamaları arasındaki fark sınanıyorsa bunlardan çekilen örneklemlerin ortalamaları üzerinde hipotez testleri yapılarak farkın doğru olup olmadığı anlaşılabilir.
Hipotez testleri için temel varsayımlar
- Örneğe alınan birimler birbirlerinden bağımsız olarak seçilmiş olmalıdırlar.
- Ana kütle normal dağılıma sahip olmalıdır.
- İki ana kütle söz konusu ise bunların varyansları eşit olmalıdır.
Hipotez testinin aşamaları
- Hipotezlerin oluşturulması nasıl yapacağım?
- Anlam düzeyinin (α- alfa) belirlenmesi.
- Örnekleme dağılımının belirlenmesi.
- Ret alanının ve kritik değerin belirlenmesi.
- Karşılaştırmalar, sonuç ve yorum.
Sıfır hipotezi (Ho)
Null, Yokluk Hipotezi, İstatistiksel Hipotez => :Örneklemden elde edilen ortalama ile anakütleye ait ortalamanın farkı "sıfır","0" sayılabilir. Yani anakütle üzerinde yapılan deformasyonların anakütle aritmetik ortalamasını değiştirmeyeceği görüşünü savunur. Bu görüş savunulurken istatistiksel anlamlılık denilen (%99 %97 veya %95) yanılgı payı göz önüne alınır. Zaten yapılan işlemlerden sonra farkın çok küçük de olsa sıfırdan farklı olduğu görülür
Karşıt Hipotez (H1)
Alternatif, Araştırma Hipotezi.:Yani yapılan deformasyonun anakütle aritmetik ortalamasını değiştireceği öngürüsüdür.
Karşılaşılabilecek durumlar
- "Ho doğrudur": Hipotez testi sonunda biz doğru olduğunu buluyoruz. Yani "reddedemiyoruz" diyoruz. Reddettiğimizde yapacağımız hatayı biliriz ama kabul ettiğimizde yapacağımız hatayı bilemeyeceğimiz için yorumlarken "reddedemiyoruz" diyoruz. ((1-α) güven katsayısı ile bu çıkardığımız sonuç doğrudur.)
- "Ho doğru" olmasına karşın hipotez testi sonunda biz onun yanlış olduğunu zannedip Ho'ı reddediyoruz. (I. tür hata veya α hata)
- "H0 hatalı veya yanlıştır": Biz onu doğru reddedemedik. Hata! (II. tür hata veya β hata)
- "H0 hatalı veya yanlıştır": Biz onun yanlış olduğunu bulduk; H0'ı reddettik. ((1-β) veya testin gücü ile bu çıkardığımız sonuç doğrudur .
"Güç", bir hipotez testinin isabetliliği için önemli bir kriterdir ve her zaman maksimize edilmek istenir. Güç'ün 1 çıkması o testin ideal olduğunu gösterir ama pratikte "Güç = 1" olan testlere çok nadir rastlanır.
I. Tür - α ve II. Tür - β tipi hatalar bilinçli olarak yapılan hatalardır. Burada bu hataların bilinçli yapılmasının sebebi olaylara bir de tersinden bakma gereksiniminden dolayıdır.
Özetle:
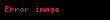 gerçek gerçek | 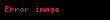 hatalı hatalı | |
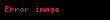 kabulu kabulu | Doğru karar çıkarım | II.Tür hata (β) |
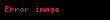 reddi reddi | I.Tür hata (α) | Doğru karar çıkarım |
Olasılıklar
α: Hatalı karar, Ho doğru, biz onu yanlış diye reddediyoruz. (I. Tip Hata)
β: Hatalı karar, Ho yanlış, biz onu doğru diye kabul ediyoruz.
(1-α) : Doğru bir Ho hipotezini kabul etmemiz olasılığı olup buna denir.
(1-β) : Yanlış bir H0 hipotezini reddetmemiz olasılığı olup buna denir.
Hipotez testi yaparken, α ve β hatalarını en aza indirmek için örneklemdeki birim sayısını olabildiğince fazlalaştırmak gerekir. α hatası yapma olasılığı azalırsa β hatası yapma olasılığı artar. İki hatanın olasılığından biri azalırken diğeri artar. Aynı testte hem α hem de β hatası beraber yapılamaz. Hatasız bir test yapmak mümkün değildir. %1,0 doğru karar verilemez. Normal dağılım asimtotik olup x-ekseni ile kesişmediği için çok küçük de olsa bir risk söz konusudur.
Tek Anakütle Ortalaması İçin Test
Burada araştırma sorunu tek bir anakütle parametresi (anakütle ortalaması) hakkındadır. Bu anakütle ortalama değeri tam olarak bilinmemekte ve belirlenen bir hipotez değerde 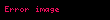
- Ho : μ = μo
alternatif hipotez ise
- Ho : μ <> μo
Bir anakütleden "basit olasılık örnekleme yöntemi" kullanarak "n" örneklem büyüklüğü olan bir örneklem ele geçirilir; istenilen değerler ölçülür ve 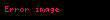
Örnek
Bir alçı dolum makinesi μo=20 kg ortalama ağırlıklı alçı dolumu yaparken arıza yapar. Tamirci getirip tamir ettirilir. Acaba yine μo=20kglık dolum yapabilecek midir?
Deneme yapıp görmek gerekir.
40 torba basit örneklem yöntemine göre seçilip bu 40 alçı torbası ağırlıkları şöyle ölçülmüştür:
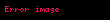
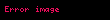
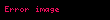
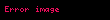

Örneklem istatistikleri şöyle hesaplanmıştır:
n = 40 torba
Örneklem ortalaması: 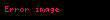
Örneklem standart sapması: σ = 3,2 kg



Buradan sonra hipotez testleri sürecine geçilir.
Hipotezler
Ho: Elimizdeki örneklem anakütle ortalaması "Mo = 20kg" olan bir anakütleden çekilmiş bir rassal örneklem olup, örneklem ortalaması X- değeri anakütle ortalamasına eşit olarak kabul edilebilir. Aradaki 1,4 kg lık fark ise tesadüfe bağlanabilecek, önemli olmayan, anlam taşımayan çok küçük bir farktır. Dolayısıyla X- = Mo yazabiliriz. Yani elimizdeki örneklemin ait olduğu anakütle ortalamasını M ile gösteririz.
H1: Bu örneklem "Mo = 20kg" olan bir anakütleden çekilmiş bir rassal örneklem olamaz. Aradaki 1,4 kg lık fark tesadüfe bağlı değil, ayarlamanın yapılmamış olması nedeni ile gerçekleşmiştir. Bu kadarlık farkın tesadüfen ortaya çıkmış olması olasılığı çok küçüktür. Dolayısıyla dolum ayarı iyi olmadığı için istenenden daha hafif ya da daha ağır dolumlarla karşılaşmamız olasıdır. Bu örneklemin çekilmiş olduğu anakütle 20 kg olamaz. Örneklemimiz kendine ait başka bir anakütleden çekilmiş olmalıdır.
İstatistiksel anlamlılık düzeyinin belirlenmesi (Risk düzeyi, Yanılgı Payı, Hata payı)
α nın saptanması.
Hatasız bir test yapamayacağımız için her testte bir miktar yanılma riskimiz vardır. Bunu 0,05; 0,01; 0,005; 0,0001;... gibi bir düzey olarak benimseyebiliriz. Yanılma payımız küçüldükçe, teste olan güven düzeyimiz yükselir. O nedenle olabildiğince az yanılma ile test yapmak isterler. Yine de α =0,05 ve α=0,01 düzeyleri en çok kullanılanlardır.
- α=0,05 olsun. Testin güven düzeyi = 1 - α = 0,95 olur.
Örnekleme dağılımının belirlenmesi
Elimizdeki veriler tartma yoluyla elde edilmiş sürekli, nitelik, nicel bir değişkene aittir. Bu tip veriler genelde normal dağılım gösterirler. Yani örneklemimiz "normal dağılım" lı bir anakütleden çekilmiştir. Anakütle sonsuz büyüklüktedir. Seçim iadesiz seçimdir ve tamamen rassal bir süreçle yapılmıştır. Yani torbaların ağırlıkları birbirini etkilememiştir. n>30 olduğu için büyük bir örneklem ile çalışıyoruz. Aynı anakütleden n=40 birimli pek çok sayıda örneklem çekmiş olsak, bunların X- ortalama dağılımı bir normal dağılım olur. Bu ortalamaların ortalaması anakütle ortalamasını verir. "kg" biriminden kurtulmak için X- ortalama değerlerini standardize edersek, verilerimiz z değerlerine dönüşür ve dağılımımız bir standart normal dağılım olan z dağılımı na dönüşür.
Ret alanının belirlenmesi
Kritik değerin saptanması
Ret alanı demek; normal dağılım eğrisi altında seçtiğimiz güven alanı (Ho'ın kabul alanı) dışında kalan Ho'ın reddedilmesini sağlayan küçük alanlardır. Ret alanı çift yönlü olabilir. (eksi taraf, artı taraf) veya tek taraflı olabilir. (Yani ya sol tarafta ya da sağ tarafta) Bunun anlaşılması için H1 hipotezine bakarız.
Test istatistiği
Elimizdeki örnekleme ait zh değeri örneklemin bir istatistiğidir. Bu istatistik yardımıyla hipotez testini sonuçlandıracağız. O nedenle, zh değerine adını veriyoruz.

- = (21,4-20)/0,51 = 2,74
Karşılaştırma, sonuç ve yorum
Bir hipotez testinde; zh< zα ise; Hokabul edilir. Bu elimizdeki X-in, M ye yakın kabul edilebilecek bir konumda (Ho'ın kabul alanında) bulunduğunu gösterir.
Eğer zh> zα ise; Horeddedilir. Elimizdeki örneklemin, Mo ortalamalı bir anakütleden çekilmiş rassal bir örneklem olmayacağı çünkü böyle bir şeyin gerçekleşmesi olasılığının çok küçük (p<0,05 veya p<0,01) olduğu sonucuna ulaşılır.
Sonuç
zh = 2,74 > z0,05 = 1,96 --> Ho RET
Bu duruma göre: elimizdeki örneklemin ortalaması, ilgilendiğim anakütlenin ortalamasından çok uzağa düşen bir büyüklüktedir. O nedenle iki ortalama arasındaki farkı z değerine dönüştürdüğümde, bulduğum zh = 2,74 değeri de z0,05 = 1,96 nın ötesine düşmüştür. Yani %5'lik ret alanına düşmüştür. Bu durumda X- = Mo biçiminde ifade ettiğim ve oradan M=Mo düzeyine yükselttiğim Ho hipotezini kabul edemem. Demek ki, bu makine hatalı dolum yapmakta, ortalaması 20 kg olan dolumlar gerçekleştirememektedir. Aynı deneyi n=40 olan 100 örneklem ile tekrarlarsam, bunun 95inde gene aynı sonuçla karşılaşmayı beklerim. Belki yalnızca 5inde makinenin ayarı iyiymiş gibi hatalı bir sonuca ulaşabilirim.
Dolayısıyla; verdiğim kararın doğru olması olasılığı %95 iken hatalı olması olasılığı en fazla %5 tir.
Test sonucundaki değerlendirmeler ve yorum
1) zh<zα olduğunda, Ho hipotezini kabul ediyoruz ve;
- Bu iki örneklemin çekilmiş olduğu anakütle ortalamalarının birbirlerine eşit olduklarını,
- Bu iki anakütlenin aynı anakütleden çekilmiş birer rassal örneklem olduğunu,
- İki örneklem ortalaması arasında gözlediğimiz farkın bir olasılık eseri olarak ortaya çıkmış, istatistik bakımından anlamlı olmayan, önemli olmayan küçük bir fark olduğunu düşünürüz.
2) zh>zα olduğunda, Ho hipotezini reddediyoruz ve;
- Ho hipotezine ait olan düşüncemizin tersini kabul ediyoruz, yani H1'i kabul ediyoruz.
- Bu büyüklükteki zh değerinin olasılığa bağlı olarak ortaya çıkmış olması olasılığı (ihtimali) çok düşüktür. Bu olasılık (p değeri) seçtiğimiz α değerinden de küçüktür. Bu kadar küçük bir olasılıkla ortaya çıkan bu z değerini artık rastgeleliğe değil anakütlenin gerçekten farklı olmasına bağlarız.
Önemli parametrik hipotez sınamaları özeti
Tek örneklem ve tek anakütle parametresi için hipotez sınamaları
| İsim | Formül | Varsayımlar |
| Tek-örneklem |  | (Normal dağılım veya n > 30) ve bilinen σ değeri. (z standard sapmalar sayı birimleri ile ölçülen ortalamaya uzaklıktır. n standard sapma aralığına düşen bir anakütlenin oranin en küçük değerini hesaplamak mümkündür; (bakin: ). |
| Tek-örneklem t-testi | 
| (Normal anakütle veya n < 30) ve bilinmeyen σ değeri |
| Tek-oran için z-testi |  | n .p > 10 ve n (1 − p) > 10 |
İki-örneklem ve iki anakütle parametresi farkı için hipotez sınamaları
| İsim | Formül | Varsayımlar |
| İki-örneklem z-testi |  | Normal dağılım ve bağımsız gözlemler ve (bilinen σ1 ve σ1 değerleri) |
| İki-örneklem pool edilmiş t-testi | 
| (Normal anakütle veya n1+n2 > 40) ve bağımsız gözlemler ve σ1 = σ2ve (bilinmeyen σ1 ve σ2 değerleri) |
| İki-örneklem pool edilmemiş t-testi | 
| (Normal anakütleler veya n1+n2 > 40) ve bağımsız gözlemler ve σ1 ≠ σ2ve (bilinmeyen σ1ve σ2 değerleri) |
| Çiftleştirilmiş t-testi | 
| (Normal farklar anakütlesi veya n < 30) ve bilinmeyen σ değeri |
| İki-oran için z-testi, eşit varyanslar | 
| n1.p1 > 5 ve n1(1 − p1) > 5 ve n2.p2 > 5 ve n2(1 − p2) > 5 ve bağımsız gözlemler |
| İki-oran için z-testi, eşit olmayan varyanslar |  | n1.p1 > 5 ve n1(1 − p1) > 5 ve n2.p2 > 5 ve n2(1 − p2) > 5 ve bağımsız gözlemler |
Sembollerin tanımlanması
= örneklem büyüklüğü
= örneklem ortalaması
= anakütle ortalaması
= anakütle standart sapması
= t istatistiği
= serbestlik derecesi
= örneklem 1 büyüklüğü
= örneklem 2 büyüklüğü
= örneklem 1 std. sapması
= örneklem 2 std. sapması
= oran 1
= oran 2
= anakütle 1 ortalaması
= anakütle 2 ortalaması
= n1 veya n2 için en küçük değer
Kaynakça
- ^ Işık, İ. (2014). Yokluk Hipotezi Anlamlılık Testi ve Etki Büyüklüğü Tartışmalarının Psikoloji Araştırmalarına Yansımaları. Eleştirel Psikoloji Bülteni, Nisan 2014, sayı: 5, sayfa:55-80. http://elestirelpsikoloji.org/wp-content/uploads/2014/11/55-80-Isik.pdf 8 Aralık 2015 tarihinde Wayback Machine sitesinde .
Dış bağlantılar
- Klasik hipotez test etmenin Bayes tipi görüşle tenkiti18 Şubat 2008 tarihinde Wayback Machine sitesinde .
- Uzun zamandan beri istatistikçileri düşündüren klasik hipotez test etmenin tenkitlerinin açığa konulması24 Kasım 2005 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Mayis 2015 Hipotez testi bir hipotezin dogrulugunun istatistiksel bir guvenilirlik araliginda saptanmasi icin kullanilan yontem Hipotez testleri bir orneklem ortalamasi ile bu orneklemin cekilmis oldugu dusunulen ortalama deger etrafindaki farkin anlamli olup olmadigini yani onemli bir fark olup olmadigini saptayan testlerdir Eger iki ana kutlenin ortalamalari arasindaki fark sinaniyorsa bunlardan cekilen orneklemlerin ortalamalari uzerinde hipotez testleri yapilarak farkin dogru olup olmadigi anlasilabilir Hipotez testleri icin temel varsayimlarOrnege alinan birimler birbirlerinden bagimsiz olarak secilmis olmalidirlar Ana kutle normal dagilima sahip olmalidir Iki ana kutle soz konusu ise bunlarin varyanslari esit olmalidir Hipotez testinin asamalari Hipotezlerin olusturulmasi nasil yapacagim Anlam duzeyinin a alfa belirlenmesi Ornekleme dagiliminin belirlenmesi Ret alaninin ve kritik degerin belirlenmesi Karsilastirmalar sonuc ve yorum Sifir hipotezi Ho Null Yokluk Hipotezi Istatistiksel Hipotez gt Orneklemden elde edilen ortalama ile anakutleye ait ortalamanin farki sifir 0 sayilabilir Yani anakutle uzerinde yapilan deformasyonlarin anakutle aritmetik ortalamasini degistirmeyecegi gorusunu savunur Bu gorus savunulurken istatistiksel anlamlilik denilen 99 97 veya 95 yanilgi payi goz onune alinir Zaten yapilan islemlerden sonra farkin cok kucuk de olsa sifirdan farkli oldugu gorulur Karsit Hipotez H1 Alternatif Arastirma Hipotezi Yani yapilan deformasyonun anakutle aritmetik ortalamasini degistirecegi ongurusudur Karsilasilabilecek durumlar Ho dogrudur Hipotez testi sonunda biz dogru oldugunu buluyoruz Yani reddedemiyoruz diyoruz Reddettigimizde yapacagimiz hatayi biliriz ama kabul ettigimizde yapacagimiz hatayi bilemeyecegimiz icin yorumlarken reddedemiyoruz diyoruz 1 a guven katsayisi ile bu cikardigimiz sonuc dogrudur Ho dogru olmasina karsin hipotez testi sonunda biz onun yanlis oldugunu zannedip Ho i reddediyoruz I tur hata veya a hata H0 hatali veya yanlistir Biz onu dogru reddedemedik Hata II tur hata veya b hata H0 hatali veya yanlistir Biz onun yanlis oldugunu bulduk H0 i reddettik 1 b veya testin gucu ile bu cikardigimiz sonuc dogrudur Guc bir hipotez testinin isabetliligi icin onemli bir kriterdir ve her zaman maksimize edilmek istenir Guc un 1 cikmasi o testin ideal oldugunu gosterir ama pratikte Guc 1 olan testlere cok nadir rastlanir I Tur a ve II Tur b tipi hatalar bilincli olarak yapilan hatalardir Burada bu hatalarin bilincli yapilmasinin sebebi olaylara bir de tersinden bakma gereksiniminden dolayidir Ozetle H0 displaystyle H 0 gercek H0 displaystyle H 0 hataliH0 displaystyle H 0 kabulu Dogru karar cikarim II Tur hata b H0 displaystyle H 0 reddi I Tur hata a Dogru karar cikarimOlasiliklara Hatali karar Ho dogru biz onu yanlis diye reddediyoruz I Tip Hata b Hatali karar Ho yanlis biz onu dogru diye kabul ediyoruz 1 a Dogru bir Ho hipotezini kabul etmemiz olasiligi olup buna denir 1 b Yanlis bir H0 hipotezini reddetmemiz olasiligi olup buna denir Hipotez testi yaparken a ve b hatalarini en aza indirmek icin orneklemdeki birim sayisini olabildigince fazlalastirmak gerekir a hatasi yapma olasiligi azalirsa b hatasi yapma olasiligi artar Iki hatanin olasiligindan biri azalirken digeri artar Ayni testte hem a hem de b hatasi beraber yapilamaz Hatasiz bir test yapmak mumkun degildir 1 0 dogru karar verilemez Normal dagilim asimtotik olup x ekseni ile kesismedigi icin cok kucuk de olsa bir risk soz konusudur Tek Anakutle Ortalamasi Icin TestBurada arastirma sorunu tek bir anakutle parametresi anakutle ortalamasi hakkindadir Bu anakutle ortalama degeri tam olarak bilinmemekte ve belirlenen bir hipotez degerde m0 displaystyle mu 0 Mu sifir diye okunur oldugu varsayilmaktadir Hipotez testi anakutle ortalamasina verilen deger hakkindadir Sifir hipotez degeri bu parametre icin belirtilen degerde oldugudur ve yani Ho m mo dd alternatif hipotez ise Ho m lt gt mo dd Bir anakutleden basit olasilik ornekleme yontemi kullanarak n orneklem buyuklugu olan bir orneklem ele gecirilir istenilen degerler olculur ve x displaystyle bar x x bar diye okunur degerindeki orneklem ortalamasi bulunur Hipotez testi yonteminde arastirma hedefi bu orneklemin soz konusu anakutleden cekilmis olup olamayacagini ya da kaynagi olan anakutleden cekilmis olabilmesinin olasiliginin ne olabilecegini ortaya koymaktir OrnekBir alci dolum makinesi mo 20 kg ortalama agirlikli alci dolumu yaparken ariza yapar Tamirci getirip tamir ettirilir Acaba yine mo 20kglik dolum yapabilecek midir Deneme yapip gormek gerekir 40 torba basit orneklem yontemine gore secilip bu 40 alci torbasi agirliklari soyle olculmustur X1 displaystyle X 1 19 8 kg X2 displaystyle X 2 20 5 kg X3 displaystyle X 3 21 2 kg X4 displaystyle X 4 18 9 kg X40 displaystyle X 40 20 8 kg Orneklem istatistikleri soyle hesaplanmistir n 40 torba Orneklem ortalamasi x displaystyle bar x 21 4 kg Orneklem standart sapmasi s 3 2 kg sx displaystyle sigma bar x 3 2 40 0 506 displaystyle 3 2 sqrt 4 0 0 506 x sx displaystyle bar x mp sigma bar x gt 21 4 0 506 kg Buradan sonra hipotez testleri surecine gecilir Hipotezler Ho Elimizdeki orneklem anakutle ortalamasi Mo 20kg olan bir anakutleden cekilmis bir rassal orneklem olup orneklem ortalamasi X degeri anakutle ortalamasina esit olarak kabul edilebilir Aradaki 1 4 kg lik fark ise tesadufe baglanabilecek onemli olmayan anlam tasimayan cok kucuk bir farktir Dolayisiyla X Mo yazabiliriz Yani elimizdeki orneklemin ait oldugu anakutle ortalamasini M ile gosteririz H1 Bu orneklem Mo 20kg olan bir anakutleden cekilmis bir rassal orneklem olamaz Aradaki 1 4 kg lik fark tesadufe bagli degil ayarlamanin yapilmamis olmasi nedeni ile gerceklesmistir Bu kadarlik farkin tesadufen ortaya cikmis olmasi olasiligi cok kucuktur Dolayisiyla dolum ayari iyi olmadigi icin istenenden daha hafif ya da daha agir dolumlarla karsilasmamiz olasidir Bu orneklemin cekilmis oldugu anakutle 20 kg olamaz Orneklemimiz kendine ait baska bir anakutleden cekilmis olmalidir Istatistiksel anlamlilik duzeyinin belirlenmesi Risk duzeyi Yanilgi Payi Hata payi a nin saptanmasi Hatasiz bir test yapamayacagimiz icin her testte bir miktar yanilma riskimiz vardir Bunu 0 05 0 01 0 005 0 0001 gibi bir duzey olarak benimseyebiliriz Yanilma payimiz kuculdukce teste olan guven duzeyimiz yukselir O nedenle olabildigince az yanilma ile test yapmak isterler Yine de a 0 05 ve a 0 01 duzeyleri en cok kullanilanlardir a 0 05 olsun Testin guven duzeyi 1 a 0 95 olur Ornekleme dagiliminin belirlenmesi Elimizdeki veriler tartma yoluyla elde edilmis surekli nitelik nicel bir degiskene aittir Bu tip veriler genelde normal dagilim gosterirler Yani orneklemimiz normal dagilim li bir anakutleden cekilmistir Anakutle sonsuz buyukluktedir Secim iadesiz secimdir ve tamamen rassal bir surecle yapilmistir Yani torbalarin agirliklari birbirini etkilememistir n gt 30 oldugu icin buyuk bir orneklem ile calisiyoruz Ayni anakutleden n 40 birimli pek cok sayida orneklem cekmis olsak bunlarin X ortalama dagilimi bir normal dagilim olur Bu ortalamalarin ortalamasi anakutle ortalamasini verir kg biriminden kurtulmak icin X ortalama degerlerini standardize edersek verilerimiz z degerlerine donusur ve dagilimimiz bir standart normal dagilim olan z dagilimi na donusur Ret alaninin belirlenmesi Kritik degerin saptanmasi Ret alani demek normal dagilim egrisi altinda sectigimiz guven alani Ho in kabul alani disinda kalan Ho in reddedilmesini saglayan kucuk alanlardir Ret alani cift yonlu olabilir eksi taraf arti taraf veya tek tarafli olabilir Yani ya sol tarafta ya da sag tarafta Bunun anlasilmasi icin H1 hipotezine bakariz Test istatistigi Elimizdeki ornekleme ait zh degeri orneklemin bir istatistigidir Bu istatistik yardimiyla hipotez testini sonuclandiracagiz O nedenle zh degerine adini veriyoruz zh x m0sn displaystyle z h frac overline x mu 0 frac sigma sqrt n 21 4 20 0 51 2 74 dd Karsilastirma sonuc ve yorum Bir hipotez testinde zh lt za ise Hokabul edilir Bu elimizdeki X in M ye yakin kabul edilebilecek bir konumda Ho in kabul alaninda bulundugunu gosterir Eger zh gt za ise Horeddedilir Elimizdeki orneklemin Mo ortalamali bir anakutleden cekilmis rassal bir orneklem olmayacagi cunku boyle bir seyin gerceklesmesi olasiliginin cok kucuk p lt 0 05 veya p lt 0 01 oldugu sonucuna ulasilir Sonuc zh 2 74 gt z0 05 1 96 gt Ho RET Bu duruma gore elimizdeki orneklemin ortalamasi ilgilendigim anakutlenin ortalamasindan cok uzaga dusen bir buyukluktedir O nedenle iki ortalama arasindaki farki z degerine donusturdugumde buldugum zh 2 74 degeri de z0 05 1 96 nin otesine dusmustur Yani 5 lik ret alanina dusmustur Bu durumda X Mo biciminde ifade ettigim ve oradan M Mo duzeyine yukselttigim Ho hipotezini kabul edemem Demek ki bu makine hatali dolum yapmakta ortalamasi 20 kg olan dolumlar gerceklestirememektedir Ayni deneyi n 40 olan 100 orneklem ile tekrarlarsam bunun 95inde gene ayni sonucla karsilasmayi beklerim Belki yalnizca 5inde makinenin ayari iyiymis gibi hatali bir sonuca ulasabilirim Dolayisiyla verdigim kararin dogru olmasi olasiligi 95 iken hatali olmasi olasiligi en fazla 5 tir Test sonucundaki degerlendirmeler ve yorum 1 zh lt za oldugunda Ho hipotezini kabul ediyoruz ve Bu iki orneklemin cekilmis oldugu anakutle ortalamalarinin birbirlerine esit olduklarini Bu iki anakutlenin ayni anakutleden cekilmis birer rassal orneklem oldugunu Iki orneklem ortalamasi arasinda gozledigimiz farkin bir olasilik eseri olarak ortaya cikmis istatistik bakimindan anlamli olmayan onemli olmayan kucuk bir fark oldugunu dusunuruz 2 zh gt za oldugunda Ho hipotezini reddediyoruz ve Ho hipotezine ait olan dusuncemizin tersini kabul ediyoruz yani H1 i kabul ediyoruz Bu buyuklukteki zh degerinin olasiliga bagli olarak ortaya cikmis olmasi olasiligi ihtimali cok dusuktur Bu olasilik p degeri sectigimiz a degerinden de kucuktur Bu kadar kucuk bir olasilikla ortaya cikan bu z degerini artik rastgelelige degil anakutlenin gercekten farkli olmasina baglariz Onemli parametrik hipotez sinamalari ozetiTek orneklem ve tek anakutle parametresi icin hipotez sinamalari Isim Formul VarsayimlarTek orneklem z x m0sn displaystyle z frac overline x mu 0 frac sigma sqrt n Normal dagilim veya n gt 30 ve bilinen s degeri z standard sapmalar sayi birimleri ile olculen ortalamaya uzakliktir n standard sapma araligina dusen bir anakutlenin oranin en kucuk degerini hesaplamak mumkundur bakin Tek orneklem t testi t x m0sn displaystyle t frac overline x mu 0 frac s sqrt n df n 1 displaystyle df n 1 Normal anakutle veya n lt 30 ve bilinmeyen s degeriTek oran icin z testi z p pp 1 p n displaystyle z frac hat p p sqrt frac p 1 p n n p gt 10 ve n 1 p gt 10Iki orneklem ve iki anakutle parametresi farki icin hipotez sinamalari Isim Formul VarsayimlarIki orneklem z testi z x 1 x 2 m1 m2 s12n1 s22n2 displaystyle z frac overline x 1 overline x 2 mu 1 mu 2 sqrt frac sigma 1 2 n 1 frac sigma 2 2 n 2 Normal dagilim ve bagimsiz gozlemler ve bilinen s1 ve s1 degerleri Iki orneklem pool edilmis t testi t x 1 x 2 m1 m2 sp1n1 1n2 displaystyle t frac overline x 1 overline x 2 mu 1 mu 2 s p sqrt frac 1 n 1 frac 1 n 2 sp2 n1 1 s12 n2 1 s22n1 n2 2 displaystyle s p 2 frac n 1 1 s 1 2 n 2 1 s 2 2 n 1 n 2 2 df n1 n2 2 displaystyle df n 1 n 2 2 Normal anakutle veya n1 n2 gt 40 ve bagimsiz gozlemler ve s1 s2ve bilinmeyen s1 ve s2 degerleri Iki orneklem pool edilmemis t testi t x 1 x 2 m1 m2 s12n1 s22n2 displaystyle t frac overline x 1 overline x 2 mu 1 mu 2 sqrt frac s 1 2 n 1 frac s 2 2 n 2 df n1 1 n2 1 n2 1 c2 n1 1 1 c 2 displaystyle df frac n 1 1 n 2 1 n 2 1 c 2 n 1 1 1 c 2 c s12n1s12n1 s22n2 displaystyle c frac frac s 1 2 n 1 frac s 1 2 n 1 frac s 2 2 n 2 veya sd min n1 n2 1 displaystyle sd min n 1 n 2 1 Normal anakutleler veya n1 n2 gt 40 ve bagimsiz gozlemler ve s1 s2ve bilinmeyen s1ve s2 degerleri Ciftlestirilmis t testi t d d0sd displaystyle t frac overline d d 0 s d sd n 1 displaystyle sd n 1 Normal farklar anakutlesi veya n lt 30 ve bilinmeyen s degeriIki oran icin z testi esit varyanslar z p1 p2p 1 p 1n1 1n2 displaystyle z frac p 1 p 2 sqrt hat p 1 hat p frac 1 n 1 frac 1 n 2 p x1 x2n1 n2 displaystyle hat p frac x 1 x 2 n 1 n 2 n1 p1 gt 5 ve n1 1 p1 gt 5 ve n2 p2 gt 5 ve n2 1 p2 gt 5 ve bagimsiz gozlemlerIki oran icin z testi esit olmayan varyanslar z p 1 p 2 p1 p2 p 1 1 p 1 n1 p 2 1 p 2 n2 displaystyle z frac hat p 1 hat p 2 p 1 p 2 sqrt frac hat p 1 1 hat p 1 n 1 frac hat p 2 1 hat p 2 n 2 n1 p1 gt 5 ve n1 1 p1 gt 5 ve n2 p2 gt 5 ve n2 1 p2 gt 5 ve bagimsiz gozlemlerSembollerin tanimlanmasi n displaystyle n orneklem buyuklugu x displaystyle overline x orneklem ortalamasi m0 displaystyle mu 0 anakutle ortalamasi s displaystyle sigma anakutle standart sapmasi t displaystyle t t istatistigi sd displaystyle sd serbestlik derecesi n1 displaystyle n 1 orneklem 1 buyuklugu n2 displaystyle n 2 orneklem 2 buyuklugu s1 displaystyle s 1 orneklem 1 std sapmasi s2 displaystyle s 2 orneklem 2 std sapmasi p1 displaystyle p 1 oran 1 p2 displaystyle p 2 oran 2 m1 displaystyle mu 1 anakutle 1 ortalamasi m2 displaystyle mu 2 anakutle 2 ortalamasi min n1 n2 displaystyle min n 1 n 2 n1 veya n2 icin en kucuk degerKaynakca Isik I 2014 Yokluk Hipotezi Anlamlilik Testi ve Etki Buyuklugu Tartismalarinin Psikoloji Arastirmalarina Yansimalari Elestirel Psikoloji Bulteni Nisan 2014 sayi 5 sayfa 55 80 http elestirelpsikoloji org wp content uploads 2014 11 55 80 Isik pdf 8 Aralik 2015 tarihinde Wayback Machine sitesinde Dis baglantilarKlasik hipotez test etmenin Bayes tipi gorusle tenkiti18 Subat 2008 tarihinde Wayback Machine sitesinde Uzun zamandan beri istatistikcileri dusunduren klasik hipotez test etmenin tenkitlerinin aciga konulmasi24 Kasim 2005 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State