Ortalama veya merkezsel konum ölçüleri, istatistik bilim dalında ve veri analizinde kullanılan bir veri dizisinin orta konumunu, tek bir sayı ile ifade eden betimsel istatistik ölçüsüdür. Günlük hayatta ortalama dendiğinde genellikle kast edilen aritmetik ortalama olmakla beraber bu ölçünün çok belirli bazı dezavantajları söz konusudur. Bu yüzden matematik ve istatistikte, bir anakütle veya örneklem veri dizisi değerlerini temsil eden tek bir orta değer veya beklenen değer, olarak medyan (ortanca), mod (tepedeğer), geometrik ortalama, harmonik ortalama vb adlari verilen birçok değişik merkezsel konum ölçüleri geliştirilmiş ve pratikte kullanılmaktadır.
Tarihçe
Ortalama kavramı başlangıçta deniz nakliyatında ortaya çıkan zarar kavramından geliştirilmiştir. Deniz nakliyatında zarar, ya zarar gören eşya sahibi tarafından özel avarya olarak tümüyle yüklenilir veya nakledilen eşyaların satış kârını ortak olarak paylaşanlar tarafından genel avarya ortaklık payına göre karşılanır. Genel avarya hesabının yapılması için geliştirilip kullanılan matematiksel hesaplar aritmetik ortalamanın ilk kullanılma alanı olmuştur. Bu kavrama Arapça avar, İtalyanca avaria, Türkçede (pek çok denizcilik terimi gibi İtalyancadan alınan) avarya ve İngilizce average adı verilmektedir. İngilizcede aynı sözcük ve bazı günlük pratik hallerde Türkçede kullanılan averaj sözcüğü ortalamaya eşit anlamda kullanılmaktadır.
İstatistikte bilimsel olarak ortalamalar kavramına bir aksiyomatik yaklaşım John Bibby (1974) tarafından verilmiştir.
Ortalama tipleri
Ortalama bir sayısal veri dizisinin merkezsel konumunu temsil etmek için seçilen tek bir sayı halinde bir özettir. Eğer veri dizisinde tüm elemanlar aynı sayı ise ortalama bu tek sayıdır. Ancak bu tip veri dizisi pratikte gayet az olarak bulunduğu, hatta nerede ise hiç bulunmadığı için, bir pratik veri dizisinin merkezsel konumunu farklı şekilde temsil edecek ortalamalar geliştirilmiştir. Önce bu ortalamalardan en çok kullanılanları kısaca ele alınacak ve sonra daha geniş kapsamlı bir tablo sunulacaktır.
En çok kullanılan ortalama tipleri
Günlük hayatta en çok kullanılan ortalama türü aritmetik ortalama olmakla birlikte, bazı durumlarda mod, medyan, geometrik ortalama ve diğer ortalama türleri tercih edilmektedir.
Aritmetik ortalama
Aritmetik ortalama bir anakütle veya bir örneklem veri değerlerinin toplamlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne bölünerek elde edilen merkezsel konum değeridir. Bu tanınım şu formülle gösterilir:
Burada 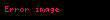
Bu yöntem istatistikte sıkça kullanılır. Fakat bazı eksik yönleri vardır.
- Verilerin ölçülme ölçeğinin aralıklı veya oransal olması gerekir. veriler için aritmetik ortalama anlamsızdır. Birçok istatistikçi veriler için aritmetik ortalamanın anlamsız olduğunu kabul etmektedirler; ancak pratikte, özellikle bir anketten ortaya çıkarılan, sırasal ölçekli veriler için aritmetik ortalama hesaplanıp önemli alanlarda kullanılmaktadır.
- Eğer anakütle veya örneklem veri dağılımı simetrik olmayıp çarpıklık gösteriyorsa, aritmetik ortalama merkezsel değer olmaktan çıkıp çarpıklık kuyruğunun bulunduğu tarafa doğru gitmeye eğilimlidir. Bu halde aritmetik ortalama istatistik bilenlerin istatistik bilmeyenlere karşı kullanabilecekleri bir aldatmaca yolu olarak da kullanılabilir.
Örnek: Bir iş yerinde işçiler maaşlarının düşük olmasından dolayı şikayetçidirler. Fakat yöneticiler tam tersini savunabilirler. Maaş dağılımları şöyle olsun:
- 1 Genel Müdür: 15.000,00 YTL
- 2 tane Genel Müdür Yardımcısı: her biri 5.500,00 YTL
- 5 tane idari işler sorumluları (Halkla ilişkiler, İnsan kaynakları...vb): her biri 1.500,00 YTL
- 30 tane normal personel = her biri 1.000,00 YTL
- Böyle bir durumda maaşların aritmetik ortalaması alınırsa
- [15000+(2x5500)+(5x1500)+(30x1000)]/38 = 1.671,05 YTL
olarak ortalama aylık maaş hesaplanır. Ama bu ortalama merkezsel konumu göstermez. 38 personelden ancak 3'ü ortalamadan fazla maaş almakta görülmektedir ve maaş dağılımı çok bariz şekilde çarpıktır. Çok küçük sayıda kişi (müdür ve 2 yardımcısı) karşılaştırılmalı olarak çok büyük değerde maaş almakta ama çok büyük sayıda kişi düşük değerde maaş almaktadır. Böylece maaş dağılımı gayet asimetrik olup sağda ince uzun bir kuyruk bulunmaktadır; veri dağılımı pozitif çarpıklık göstermektedir. Bu nedenle maaş aritmetik ortalaması merkezsel konum göstergesi olmaktan çıkmıştır.
GRiS
Aritmetik Ortalama'nın Çarpık veri dizilerinde işlevini kaybetmesi durumunun önüne geçebilmek için, 2014 yılında yayınlanan "İstatistikte Altın Oran" Kitabında yeni bir ortalama tanımlanmıştır. Bu yeni ortalama GRiS (Golden Ratio in Statistics) Ortalama olarak adlandırılmıştır. Bu ortalamanın özelliği, veri dizisindeki her bir elemanın, konumuna göre katkı sağlamasıdır.

Veri Dizisi küçükten büyüğe sıralandıktan sonra, her bir elemana bulunduğu konuma göre, yukarıda gösterilen GRiS ortalama katsayı maskesindeki ağırlıklandırma katsayıları atanır. Her bir elemanın Medyan'dan farkı, kendine atanmış ağırlıklandırma katsayısı ile çarpılır, bu çarpımların toplamı, ağırlıklandırma katsayıları toplamına bölünür ve medyandan sapma hesaplanır. Veri dizisinin her iki ucunda bulunan elemanlar, aynı ölçüde baskılandığı için; GRiS ortalama her durumda medyana, aritmetik ortalamadan daha yakın konumlanmaktadır. Bu yöntem sayesinde aritmetik ortalamanın en bariz zayıflığı olan merkezsel değer olmaktan çıkıp çarpıklık kuyruğunun bulunduğu tarafa doğru gitme eğilimi bertaraf edilmiştir.
Geometrik ortalama
Geometrik ortalama bir anakütle veya bir örneklem veri değerlerinin çarpımlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne eşit kökü alınmak suretiyle elde edilen bir merkezsel konum değeridir. Bu tanımlama için formül şöyle verilir:
Burada G geometrik ortalama sembolüdür.
Bu tür ortalamanın da dezavantajları bulunmaktadır:
- Büyük bir sayıda kök almak el hesabı ile imkânsız olduğu için bu tür ortalama genel olarak elektronik hesap makinelerinin veya bilgisayarların gelişmesinden önce kullanılması çok zor olmaktaydı. Verilerin logaritması alınıp bu logaritma verilerinin toplamı bulunduktan sonra eldeki veri büyüklük sayısına bölünerek geometrik ortalamanın logaritma değeri bulunur, bunun antilogaritmasının alınması gerekirdi. Orta basitlikte hesaplar yapabilen elektronik hesap makinaları veya kompüter kullanılarak geometrik ortalama almak çok kolaylaşmıştır.
- Geometrik ortalama bulabilmek için verilerin pozitif değerde olması gerekmektedir yani veri değerlerinin özellikle sıfır veya negatif olmaması gerekmektedir. Eğer tek bir veri değeri sıfır ise, geometrik ortalama almak anlamsız olacaktır.
- Ayrıca verilerin ölçülme ölçeğinin oransal olması gerekir; (isimsel ölçekli), (sırasal ölçekli) ve (aralıksal ölçekli) veri değerleri için geometrik ortalama anlamsız olur.
Mod
Mod veri dizisi içinde en çok defa tekrarlanan veri değeridir. Mod (isimsel ölçekli) veriler için anlamlı olan tek ortalama ölçüsüdür. Ancak veri dizisi içinde tek bir mod olmayabilir yahut birden fazla sayıda mod bulunabilir.
Medyan
- Ana madde: Medyan
Medyan bir veri dizisinin küçükten büyüğe veya büyükten küçüğe sıralanmasından sonra bu dizinin tam ortasında bulunan değerdir. Eğer veri büyüklüğü tek sayılı ise medyan verilen bir veri değerine eşit olur. Eğer veri büyüklüğü çift sayılı ise medyan orta iki değerin ortalaması olur. Medyan bulmak için basit bir algoritmaya göre sıralanmış veri değerlerinin kalan en küçük ve en büyük değerleri birer birer elimine edilir; veri sayısı tek ise en son kalan tek veri medyandır; eğer veri sayısı çift ise son kalan iki veri çiftinin ortalaması medyan olur.
Genelleştirilmiş ortalama türleri
İstatistikçiler ortalama türlerini genelleştiren tek bir formül bulmak için değişik yaklaşımlar kullanmışlardır:
- Genelleştirilmiş ortalama formülü şöyle verilir:
Bu formülde m için değişik değerler değişik ortalama türü verirler: :
- eğer m = 1 ise aritmetik ortalama;
- eğer m = 2 ise kuadratik ortalama;
- eğer m = -1 ise harmonik ortalama;
- limit m → 0 ise
geometrik ortalamaya yaklaşır.
- Genelleştirilmiş f-ortalaması formülü diğer bir örnektir. Genelleştirilmiş f-ortalaması için formül şudur:
Burada f tersi alınabilir bir fonksiyondur. Bu formül değişik ortalamalar için şu şekilleri alır:
- Geometrik ortalama için f(x)=log x olur.
- Harmonik ortalama için f(x)= 1/x olur.
- Çok az bilinen üstel ortalama için f(x)=ex olur.
Ancak bu genelleştirme ile tüm ortalamaların ayrı ayrı formüllerini bulmak imkânsızdır.
- Diğer bir genelleştirme, ortalamalar listesi elamanlarının permütasyonu halinde simetrik olan bir g(x1, x2, ..., xn) fonksiyonunun değişik şekillerde ifadesi ile yapılır:
- Aritmetik ortalama için g(x1, x2, ..., xn) =x1+x2+ ...+ xn.
- Geometrik ortalama için g(x1, x2, ..., xn) =x1·x2· ...· xn.
- Harmonik ortalama için g(x1, x2, ..., xn) =x1−1+x2−1+ ...+ xn−1.
Değişik ortalama tipleri özeti
İstatistik bilim dalında bir sıra değişik ortalama tipleri geliştirilmiş ve bunlardan araştırıcının isteğine göre birinin veya birkaçının eldeki veriler için merkezsel konum ölçüsü olarak kullanılması imkânı sağlanmıştır.
| İsim | Denklem veya betimleme |
|---|---|
| Aritmetik ortalama |  |
| Medyan (ortanca) | Bu yüksek değerde olan veriler ile düşük değerde olan verilerin tam ortasında bulunan bir sayı. |
| Geometrik medyan | Rn düzeyindeki noktalar için, medyan kavramının, matematik rotasyon dönüşümünde sabit kalan bir genişletilmesi, |
| Mod (tepedeğer) | Verilerin en çok defa tekrarlanmış değeri |
| Geometrik ortalama |  |
| Harmonik ortalama |  |
| Kuadratik ortalama (veya ortalama kareler karekökü) |  |
| Genelleştirilmiş ortalama |  |
| Ağırlıklı ortalama |  |
| Belirli bir yüzde oranda en yüksek ve en düşük veri değerlerinin bertaraf edilmelerinden sonra hesaplanan aritmetik ortalamadır. | |
| Çeyrekler açıklığı kullanılarak kesilmiş ortalamanın özel bir hali. | |
 | |
| Bir çeşit kesilmiş ortalama olup belirli bir yüzde olarak kesilen en yüksek ve en düşük değerler bertaraf edileceğine kalan sayılar için en yuksek ve en düşük veri değerleri yerine ikame edilirler. | |
 |
Ayrıca bakınız
Kaynakça
- ^ Bibby, J. (1974) "Axiomatisations of the average and a further generalization of monotonic sequences" Glasgow Mathematical Journal C.15, say.63–65.
- ^ Gunver, Mehmet Guven; Senocak, Mustafa Sukru; Vehid, Suphi. "TO DETERMINE SKEWNESS, MEAN AND DEVIATION WITH A NEW APPROACH ON CONTINUOUS DATA" 2 Haziran 2018 tarihinde Wayback Machine sitesinde .. PONTE International Scientific Researchs Journal. 73 (2). doi:10.21506/j.ponte.2017.2.34
- ^ Mehmet Güven GÜNVER, Prof. Dr. Mustafa Şükrü ŞENOCAK, Doç Dr. Suphi VEHİD, İstatistikte Altın Oran, Türkmen Kitabevi, 2014, ISBN : 9786054749409
- ^ Bakın Bibby,J. (1974) "Axiomatisations of the average and a further generalisation of monotonic sequences", Glasgow Mathematical Journal, C.15, say. 63–65,
- Spiegel, Murray R ve Stephens, Larry J. (Tr.Çev.: Çelebioğlu, Salih) (2013) İstatistik, İstanbul: Nobel Akademik Yayıncılık
Dış bağlantılar
- (İngilizce)
- İki değer için aritmetik ortalama ve geometrik ortalama hesaplanması ve karşılaştırılması27 Kasım 2010 tarihinde Wayback Machine sitesinde . (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Ortalama veya merkezsel konum olculeri istatistik bilim dalinda ve veri analizinde kullanilan bir veri dizisinin orta konumunu tek bir sayi ile ifade eden betimsel istatistik olcusudur Gunluk hayatta ortalama dendiginde genellikle kast edilen aritmetik ortalama olmakla beraber bu olcunun cok belirli bazi dezavantajlari soz konusudur Bu yuzden matematik ve istatistikte bir anakutle veya orneklem veri dizisi degerlerini temsil eden tek bir orta deger veya beklenen deger olarak medyan ortanca mod tepedeger geometrik ortalama harmonik ortalama vb adlari verilen bircok degisik merkezsel konum olculeri gelistirilmis ve pratikte kullanilmaktadir TarihceOrtalama kavrami baslangicta deniz nakliyatinda ortaya cikan zarar kavramindan gelistirilmistir Deniz nakliyatinda zarar ya zarar goren esya sahibi tarafindan ozel avarya olarak tumuyle yuklenilir veya nakledilen esyalarin satis karini ortak olarak paylasanlar tarafindan genel avarya ortaklik payina gore karsilanir Genel avarya hesabinin yapilmasi icin gelistirilip kullanilan matematiksel hesaplar aritmetik ortalamanin ilk kullanilma alani olmustur Bu kavrama Arapca avar Italyanca avaria Turkcede pek cok denizcilik terimi gibi Italyancadan alinan avarya ve Ingilizce average adi verilmektedir Ingilizcede ayni sozcuk ve bazi gunluk pratik hallerde Turkcede kullanilan averaj sozcugu ortalamaya esit anlamda kullanilmaktadir Istatistikte bilimsel olarak ortalamalar kavramina bir aksiyomatik yaklasim John Bibby 1974 tarafindan verilmistir Ortalama tipleriOrtalama bir sayisal veri dizisinin merkezsel konumunu temsil etmek icin secilen tek bir sayi halinde bir ozettir Eger veri dizisinde tum elemanlar ayni sayi ise ortalama bu tek sayidir Ancak bu tip veri dizisi pratikte gayet az olarak bulundugu hatta nerede ise hic bulunmadigi icin bir pratik veri dizisinin merkezsel konumunu farkli sekilde temsil edecek ortalamalar gelistirilmistir Once bu ortalamalardan en cok kullanilanlari kisaca ele alinacak ve sonra daha genis kapsamli bir tablo sunulacaktir En cok kullanilan ortalama tipleri Gunluk hayatta en cok kullanilan ortalama turu aritmetik ortalama olmakla birlikte bazi durumlarda mod medyan geometrik ortalama ve diger ortalama turleri tercih edilmektedir Aritmetik ortalama Aritmetik ortalama bir anakutle veya bir orneklem veri degerlerinin toplamlarinin o anakutledeki terim sayisina veya orneklem buyuklugune bolunerek elde edilen merkezsel konum degeridir Bu taninim su formulle gosterilir x 1n i 1nxi displaystyle bar x 1 over n sum i 1 n x i Burada x displaystyle bar x orneklem aritmetik ortalamasi semboludur anakutle aritmetik ortalamasi icin m kullanilir Bu yontem istatistikte sikca kullanilir Fakat bazi eksik yonleri vardir Verilerin olculme olceginin aralikli veya oransal olmasi gerekir veriler icin aritmetik ortalama anlamsizdir Bircok istatistikci veriler icin aritmetik ortalamanin anlamsiz oldugunu kabul etmektedirler ancak pratikte ozellikle bir anketten ortaya cikarilan sirasal olcekli veriler icin aritmetik ortalama hesaplanip onemli alanlarda kullanilmaktadir Eger anakutle veya orneklem veri dagilimi simetrik olmayip carpiklik gosteriyorsa aritmetik ortalama merkezsel deger olmaktan cikip carpiklik kuyrugunun bulundugu tarafa dogru gitmeye egilimlidir Bu halde aritmetik ortalama istatistik bilenlerin istatistik bilmeyenlere karsi kullanabilecekleri bir aldatmaca yolu olarak da kullanilabilir Ornek Bir is yerinde isciler maaslarinin dusuk olmasindan dolayi sikayetcidirler Fakat yoneticiler tam tersini savunabilirler Maas dagilimlari soyle olsun 1 Genel Mudur 15 000 00 YTL 2 tane Genel Mudur Yardimcisi her biri 5 500 00 YTL 5 tane idari isler sorumlulari Halkla iliskiler Insan kaynaklari vb her biri 1 500 00 YTL 30 tane normal personel her biri 1 000 00 YTL Boyle bir durumda maaslarin aritmetik ortalamasi alinirsa 15000 2x5500 5x1500 30x1000 38 1 671 05 YTL olarak ortalama aylik maas hesaplanir Ama bu ortalama merkezsel konumu gostermez 38 personelden ancak 3 u ortalamadan fazla maas almakta gorulmektedir ve maas dagilimi cok bariz sekilde carpiktir Cok kucuk sayida kisi mudur ve 2 yardimcisi karsilastirilmali olarak cok buyuk degerde maas almakta ama cok buyuk sayida kisi dusuk degerde maas almaktadir Boylece maas dagilimi gayet asimetrik olup sagda ince uzun bir kuyruk bulunmaktadir veri dagilimi pozitif carpiklik gostermektedir Bu nedenle maas aritmetik ortalamasi merkezsel konum gostergesi olmaktan cikmistir GRiS Aritmetik Ortalama nin Carpik veri dizilerinde islevini kaybetmesi durumunun onune gecebilmek icin 2014 yilinda yayinlanan Istatistikte Altin Oran Kitabinda yeni bir ortalama tanimlanmistir Bu yeni ortalama GRiS Golden Ratio in Statistics Ortalama olarak adlandirilmistir Bu ortalamanin ozelligi veri dizisindeki her bir elemanin konumuna gore katki saglamasidir GRiS ortalama katsayi maskesi Veri Dizisi kucukten buyuge siralandiktan sonra her bir elemana bulundugu konuma gore yukarida gosterilen GRiS ortalama katsayi maskesindeki agirliklandirma katsayilari atanir Her bir elemanin Medyan dan farki kendine atanmis agirliklandirma katsayisi ile carpilir bu carpimlarin toplami agirliklandirma katsayilari toplamina bolunur ve medyandan sapma hesaplanir Veri dizisinin her iki ucunda bulunan elemanlar ayni olcude baskilandigi icin GRiS ortalama her durumda medyana aritmetik ortalamadan daha yakin konumlanmaktadir Bu yontem sayesinde aritmetik ortalamanin en bariz zayifligi olan merkezsel deger olmaktan cikip carpiklik kuyrugunun bulundugu tarafa dogru gitme egilimi bertaraf edilmistir Geometrik ortalama Geometrik ortalama bir anakutle veya bir orneklem veri degerlerinin carpimlarinin o anakutledeki terim sayisina veya orneklem buyuklugune esit koku alinmak suretiyle elde edilen bir merkezsel konum degeridir Bu tanimlama icin formul soyle verilir G x1 x2 xnn i 1nxin displaystyle G sqrt n x 1 cdot x 2 cdot ldots cdot x n sqrt n prod i 1 n x i Burada G geometrik ortalama semboludur Bu tur ortalamanin da dezavantajlari bulunmaktadir Buyuk bir sayida kok almak el hesabi ile imkansiz oldugu icin bu tur ortalama genel olarak elektronik hesap makinelerinin veya bilgisayarlarin gelismesinden once kullanilmasi cok zor olmaktaydi Verilerin logaritmasi alinip bu logaritma verilerinin toplami bulunduktan sonra eldeki veri buyukluk sayisina bolunerek geometrik ortalamanin logaritma degeri bulunur bunun antilogaritmasinin alinmasi gerekirdi Orta basitlikte hesaplar yapabilen elektronik hesap makinalari veya komputer kullanilarak geometrik ortalama almak cok kolaylasmistir Geometrik ortalama bulabilmek icin verilerin pozitif degerde olmasi gerekmektedir yani veri degerlerinin ozellikle sifir veya negatif olmamasi gerekmektedir Eger tek bir veri degeri sifir ise geometrik ortalama almak anlamsiz olacaktir Ayrica verilerin olculme olceginin oransal olmasi gerekir isimsel olcekli sirasal olcekli ve araliksal olcekli veri degerleri icin geometrik ortalama anlamsiz olur Mod Mod veri dizisi icinde en cok defa tekrarlanan veri degeridir Mod isimsel olcekli veriler icin anlamli olan tek ortalama olcusudur Ancak veri dizisi icinde tek bir mod olmayabilir yahut birden fazla sayida mod bulunabilir Medyan Ana madde Medyan Medyan bir veri dizisinin kucukten buyuge veya buyukten kucuge siralanmasindan sonra bu dizinin tam ortasinda bulunan degerdir Eger veri buyuklugu tek sayili ise medyan verilen bir veri degerine esit olur Eger veri buyuklugu cift sayili ise medyan orta iki degerin ortalamasi olur Medyan bulmak icin basit bir algoritmaya gore siralanmis veri degerlerinin kalan en kucuk ve en buyuk degerleri birer birer elimine edilir veri sayisi tek ise en son kalan tek veri medyandir eger veri sayisi cift ise son kalan iki veri ciftinin ortalamasi medyan olur Genellestirilmis ortalama turleri Istatistikciler ortalama turlerini genellestiren tek bir formul bulmak icin degisik yaklasimlar kullanmislardir Genellestirilmis ortalama formulu soyle verilir x m 1n i 1nximm displaystyle bar x m sqrt m frac 1 n sum i 1 n x i m Bu formulde m icin degisik degerler degisik ortalama turu verirler eger m 1 ise aritmetik ortalama eger m 2 ise kuadratik ortalama eger m 1 ise harmonik ortalama limit m 0 ise x m displaystyle bar x m geometrik ortalamaya yaklasir Genellestirilmis f ortalamasi formulu diger bir ornektir Genellestirilmis f ortalamasi icin formul sudur y f 1 f x1 f x2 f xn n displaystyle y f 1 left frac f x 1 f x 2 cdots f x n n right Burada f tersi alinabilir bir fonksiyondur Bu formul degisik ortalamalar icin su sekilleri alir Geometrik ortalama icin f x log x olur Harmonik ortalama icin f x 1 x olur Cok az bilinen ustel ortalama icin f x ex olur Ancak bu genellestirme ile tum ortalamalarin ayri ayri formullerini bulmak imkansizdir Diger bir genellestirme ortalamalar listesi elamanlarinin permutasyonu halinde simetrik olan bir g x1 x2 xn fonksiyonunun degisik sekillerde ifadesi ile yapilir Aritmetik ortalama icin g x1 x2 xn x1 x2 xn Geometrik ortalama icin g x1 x2 xn x1 x2 xn Harmonik ortalama icin g x1 x2 xn x1 1 x2 1 xn 1 Degisik ortalama tipleri ozeti Istatistik bilim dalinda bir sira degisik ortalama tipleri gelistirilmis ve bunlardan arastiricinin istegine gore birinin veya birkacinin eldeki veriler icin merkezsel konum olcusu olarak kullanilmasi imkani saglanmistir Isim Denklem veya betimlemeAritmetik ortalama x 1n i 1nxi 1n x1 xn displaystyle bar x frac 1 n sum i 1 n x i frac 1 n x 1 cdots x n Medyan ortanca Bu yuksek degerde olan veriler ile dusuk degerde olan verilerin tam ortasinda bulunan bir sayi Geometrik medyan Rn duzeyindeki noktalar icin medyan kavraminin matematik rotasyon donusumunde sabit kalan bir genisletilmesi Mod tepedeger Verilerin en cok defa tekrarlanmis degeriGeometrik ortalama i 1nxi 1 n x1 x2 xnn displaystyle bigg prod i 1 n x i bigg 1 n sqrt n x 1 cdot x 2 dotsb x n Harmonik ortalama n1x1 1x2 1xn displaystyle frac n frac 1 x 1 frac 1 x 2 cdots frac 1 x n Kuadratik ortalama veya ortalama kareler karekoku 1n i 1nxi2 x12 x22 xn2n displaystyle sqrt frac 1 n sum i 1 n x i 2 sqrt frac x 1 2 x 2 2 cdots x n 2 n Genellestirilmis ortalama 1n i 1nximm displaystyle sqrt m frac 1 n cdot sum i 1 n x i m Agirlikli ortalama i 1nwixi i 1nwi w1x1 w2x2 wnxnw1 w2 wn displaystyle frac sum i 1 n w i x i sum i 1 n w i frac w 1 x 1 w 2 x 2 cdots w n x n w 1 w 2 cdots w n Belirli bir yuzde oranda en yuksek ve en dusuk veri degerlerinin bertaraf edilmelerinden sonra hesaplanan aritmetik ortalamadir Ceyrekler acikligi kullanilarak kesilmis ortalamanin ozel bir hali maxx minx2 displaystyle frac max x min x 2 Bir cesit kesilmis ortalama olup belirli bir yuzde olarak kesilen en yuksek ve en dusuk degerler bertaraf edilecegine kalan sayilar icin en yuksek ve en dusuk veri degerleri yerine ikame edilirler 1 1 Rt 1 ti displaystyle 1 prod 1 Rt 1 sum t i Ayrica bakinizAritmetik ortalamaKaynakca Bibby J 1974 Axiomatisations of the average and a further generalization of monotonic sequences Glasgow Mathematical Journal C 15 say 63 65 Gunver Mehmet Guven Senocak Mustafa Sukru Vehid Suphi TO DETERMINE SKEWNESS MEAN AND DEVIATION WITH A NEW APPROACH ON CONTINUOUS DATA 2 Haziran 2018 tarihinde Wayback Machine sitesinde PONTE International Scientific Researchs Journal 73 2 doi 10 21506 j ponte 2017 2 34 Mehmet Guven GUNVER Prof Dr Mustafa Sukru SENOCAK Doc Dr Suphi VEHID Istatistikte Altin Oran Turkmen Kitabevi 2014 ISBN 9786054749409 Bakin Bibby J 1974 Axiomatisations of the average and a further generalisation of monotonic sequences Glasgow Mathematical Journal C 15 say 63 65 Spiegel Murray R ve Stephens Larry J Tr Cev Celebioglu Salih 2013 Istatistik Istanbul Nobel Akademik Yayincilik ISBN 9786051337043Dis baglantilar Ingilizce Iki deger icin aritmetik ortalama ve geometrik ortalama hesaplanmasi ve karsilastirilmasi27 Kasim 2010 tarihinde Wayback Machine sitesinde Ingilizce
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State