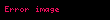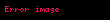Olasılık kuramı ve istatistik bilim dallarında Laplace dağılımı Pierre-Simon Laplace anısına isimlendirilmiş bir sürekli olasılık dağılımıdır. Arka arkaya birbiriyle yapıştırılmış şekilde ve bir de konum parametresi dahil edilerek birleştirilmiş iki üstel dağılımdan oluştuğu için, çift üstel dağılımı adı ile de anılmaktadır. İki bağımsız ve tıpatıp aynı şekilde üstel dağılım gösteren bir rassal değişken bir Laplace dağılımı ile işlev görürler. Bu, aynen üstel dağılım gösteren rassal zamanda değerlendirilen benzer.
Olasılık yoğunluk fonksiyonu | |
Yığmalı dağılım fonksiyonu | |
| Parametreler | (reel) (reel) |
|---|---|
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | metine bakın |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | for |
| Karakteristik fonksiyon | |
Karekteristikler
Olasılık yoğunluk fonksiyonu
Eğer bir rassal değişken şu olasılık yoğunluk fonksiyonu gösteriyorsa, o rassal değişken bir Laplace(μ,b) dağılımı gösterir:
Burada, μ ve b > 0 olurlar. Eğer μ = 0 ve b = 1, pozitif yarı-doğru tıpatıp 1/2 oran ile ölçeklenmiş bir üstel dağılımdır.
Laplace dağılımı için olasılık yoğunluk fonksiyonu bir normal dağılımı anımsatmaktadır. Fakat normal dağılım ortalama μdan farkın karesi terimleri ile ifade edilirken, buna karşılık Laplace dağılım yoğunluğu ortalamadan mutlak farklar terimleri ile ifade edilmektedirler. Sonuç olarak normal dağılıma nazaran Laplace dağılım daha şişkin kuyruklar gösterir.
Yığmalı dağılım fonksiyonu
(Eğer iki simetrik hal görülüp ayırt edilirlerse), Laplace dağılımının integralinin alınması kolaydır. Çünkü bu işlem için mutlak değer fonksiyonu kullanılır. Böylece yığmalı dağılım fonksiyonu şöyle bulunur:
 |  |
 | |
 |
Ters yığmalı dağılım fonksiyonu şöyle verilir:
Laplace değişebilirlerinin üretilmesi
Bir rassal değişken olan Unun (-1/2, 1/2] aralığında bulunan çekilmiş olduğu bilinirse, şu değişebilir
μ ve b parametreleri olan bir Laplace dağılımı gösterir. Bu sonuç yukarıda verilen ters yığmalı dağılım fonksiyonundan hemen çıkartılır.
Bir Laplace(0,b) değişebilir Üstel(1/b) dağılım gösteren iki arasındaki fark olarak üretilebilir. Buna eşit olan bir şekilde, bir Laplace(0,1) değişebilir, tekdüze dağılım gösteren iki bağımsız ve aynen dağılım gösteren rassal değişkenlerin oranının olarak üretilebilir.
Parametre kestirimi
N sayıda bağımsız ve aynı şekilde dağılım gösteren örneklemler x1, x2, ..., xN olarak verilsin, 

Bu bir kestirimcisidir.
Momentler
İlişkili dağılımlar
- Eğer
ise, o zaman
bir üstel dağılım gösterir.
- Eğer
ve
den bağımsız olan
iseler, o halde

- Eğer
ve
dan bağımsız olan
ise, o halde
olur .
İç kaynaklar
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve istatistik bilim dallarinda Laplace dagilimi Pierre Simon Laplace anisina isimlendirilmis bir surekli olasilik dagilimidir Arka arkaya birbiriyle yapistirilmis sekilde ve bir de konum parametresi dahil edilerek birlestirilmis iki ustel dagilimdan olustugu icin cift ustel dagilimi adi ile de anilmaktadir Iki bagimsiz ve tipatip ayni sekilde ustel dagilim gosteren bir rassal degisken bir Laplace dagilimi ile islev gorurler Bu aynen ustel dagilim gosteren rassal zamanda degerlendirilen benzer Laplace Olasilik yogunluk fonksiyonuYigmali dagilim fonksiyonuParametreler m displaystyle mu reel b gt 0 displaystyle b gt 0 reel x displaystyle x in infty infty Olasilik yogunluk fonksiyonu OYF 12bexp x m b displaystyle frac 1 2 b exp left frac x mu b right Birikimli dagilim fonksiyonu YDF metine bakinOrtalama m displaystyle mu Medyan m displaystyle mu Mod m displaystyle mu Varyans 2b2 displaystyle 2 b 2 Carpiklik 0 displaystyle 0 Fazladan basiklik 3 displaystyle 3 Entropi log2 2eb displaystyle log 2 2 e b Moment ureten fonksiyon mf exp mt 1 b2t2 displaystyle frac exp mu t 1 b 2 t 2 for t lt 1 b displaystyle t lt 1 b Karakteristik fonksiyon exp mit 1 b2t2 displaystyle frac exp mu i t 1 b 2 t 2 KarekteristiklerOlasilik yogunluk fonksiyonu Eger bir rassal degisken su olasilik yogunluk fonksiyonu gosteriyorsa o rassal degisken bir Laplace m b dagilimi gosterir f x m b 12bexp x m b displaystyle f x mu b frac 1 2b exp left frac x mu b right 12b exp m xb if x lt mexp x mb if x m displaystyle frac 1 2b left begin matrix exp left frac mu x b right amp mbox if x lt mu 8pt exp left frac x mu b right amp mbox if x geq mu end matrix right dd Burada m ve b gt 0 olurlar Eger m 0 ve b 1 pozitif yari dogru tipatip 1 2 oran ile olceklenmis bir ustel dagilimdir Laplace dagilimi icin olasilik yogunluk fonksiyonu bir normal dagilimi animsatmaktadir Fakat normal dagilim ortalama mdan farkin karesi terimleri ile ifade edilirken buna karsilik Laplace dagilim yogunlugu ortalamadan mutlak farklar terimleri ile ifade edilmektedirler Sonuc olarak normal dagilima nazaran Laplace dagilim daha siskin kuyruklar gosterir Yigmali dagilim fonksiyonu Eger iki simetrik hal gorulup ayirt edilirlerse Laplace dagiliminin integralinin alinmasi kolaydir Cunku bu islem icin mutlak deger fonksiyonu kullanilir Boylece yigmali dagilim fonksiyonu soyle bulunur F x displaystyle F x xf u du displaystyle int infty x f u mathrm d u 12exp m xb if x lt m1 12exp x mb if x m displaystyle left begin matrix amp frac 1 2 exp left frac mu x b right amp mbox if x lt mu 8pt 1 amp frac 1 2 exp left frac x mu b right amp mbox if x geq mu end matrix right 0 5 1 sgn x m 1 exp x m b displaystyle 0 5 1 operatorname sgn x mu 1 exp x mu b Ters yigmali dagilim fonksiyonu soyle verilir F 1 p m bsgn p 0 5 ln 1 2 p 0 5 displaystyle F 1 p mu b operatorname sgn p 0 5 ln 1 2 p 0 5 Laplace degisebilirlerinin uretilmesiBir rassal degisken olan Unun 1 2 1 2 araliginda bulunan cekilmis oldugu bilinirse su degisebilir X m bsgn U ln 1 2 U displaystyle X mu b operatorname sgn U ln 1 2 U m ve b parametreleri olan bir Laplace dagilimi gosterir Bu sonuc yukarida verilen ters yigmali dagilim fonksiyonundan hemen cikartilir Bir Laplace 0 b degisebilir Ustel 1 b dagilim gosteren iki arasindaki fark olarak uretilebilir Buna esit olan bir sekilde bir Laplace 0 1 degisebilir tekduze dagilim gosteren iki bagimsiz ve aynen dagilim gosteren rassal degiskenlerin oraninin olarak uretilebilir Parametre kestirimiN sayida bagimsiz ve ayni sekilde dagilim gosteren orneklemler x1 x2 xN olarak verilsin m displaystyle mu un kestirimcisi yani m displaystyle hat mu olarak orneklem medyani alinsin o halde b parametresinin kestirimcisi su olur b 1N i 1N xi m displaystyle hat b frac 1 N sum i 1 N x i hat mu Bu bir kestirimcisidir Momentlermr 12 k 0r r k r k bkm r k k 1 1 k displaystyle mu r bigg frac 1 2 bigg sum k 0 r bigg frac r k r k b k mu r k k 1 1 k bigg Iliskili dagilimlarEger X Laplace 0 b displaystyle X sim mathrm Laplace 0 b ise o zaman X Ustel b 1 displaystyle X sim mathrm Ustel b 1 bir ustel dagilim gosterir Eger X Ustel l displaystyle X sim mathrm Ustel lambda ve X displaystyle X den bagimsiz olan Y Bernoulli 0 5 displaystyle Y sim mathrm Bernoulli 0 5 iseler o halde X 2Y 1 Laplace 0 l 1 displaystyle X 2Y 1 sim mathrm Laplace 0 lambda 1 olur Eger X1 Ustel l1 displaystyle X 1 sim mathrm Ustel lambda 1 ve X1 displaystyle X 1 dan bagimsiz olan X2 Ustel l2 displaystyle X 2 sim mathrm Ustel lambda 2 ise o haldel1X1 l2X2 Laplace 0 1 displaystyle lambda 1 X 1 lambda 2 X 2 sim mathrm Laplace left 0 1 right olur Ic kaynaklarKaynakca ol section
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans